Lower Bounds and Optimal Algorithms for Non-Smooth Convex Decentralized Optimization over Time-Varying Networks

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in decentralized optimization because it fills a critical gap in the understanding of non-smooth convex optimization over time-varying networks. It provides the first lower bounds and matching optimal algorithms, advancing the field significantly and paving the way for more efficient solutions in various applications such as distributed machine learning and network resource allocation.

Visual Insights

#

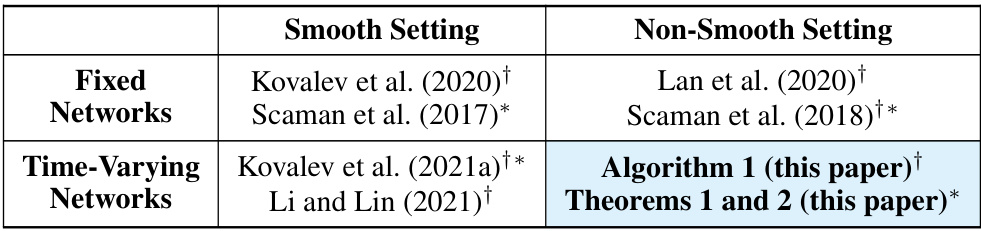
This table summarizes the existing state-of-the-art results in decentralized convex optimization, categorized by whether the setting uses smooth or non-smooth objective functions and fixed or time-varying networks. It indicates which papers established lower complexity bounds (*) and which provided optimal algorithms that matched those lower bounds (†). The table highlights the gap in the literature that this paper addresses: the lack of lower bounds and optimal algorithms for non-smooth decentralized optimization over time-varying networks.

In-depth insights

#

Optimal Decentralized Algo

#

Optimal decentralized algorithms aim to solve optimization problems across a network of nodes efficiently and in a distributed manner. Optimality typically refers to achieving the best possible performance given certain constraints, like communication bandwidth or computational power at individual nodes. These algorithms are crucial in various applications where centralized approaches are infeasible, such as multi-agent systems, sensor networks, and federated learning. Key challenges include dealing with communication delays, handling unreliable network connections, and ensuring convergence to a global optimum despite local computations. Designing optimal algorithms often involves sophisticated techniques from distributed optimization, such as gradient tracking, consensus algorithms, and dual decomposition. Analyzing the communication and computation complexity is critical to determine their efficiency. Future research directions could focus on developing algorithms robust to more realistic network conditions (e.g., dynamic topologies, Byzantine failures), improving the convergence rates for non-convex problems, and applying these algorithms to increasingly complex real-world applications.

Time-Varying Network Bound

#

The concept of a “Time-Varying Network Bound” in decentralized optimization is crucial because it addresses the challenges of dynamic network topologies. Traditional decentralized optimization methods often assume static networks, where communication links remain constant. However, real-world networks, especially in distributed systems or sensor networks, are often dynamic, with links appearing and disappearing over time. A time-varying network bound would quantify the impact of this dynamism on the convergence rate and communication complexity of optimization algorithms. The bound would help to determine the minimum number of communication rounds or the minimum amount of computation needed to reach a desired level of accuracy. This is particularly important for resource-constrained devices where minimizing communication is essential. Research in this area aims to develop novel algorithms that can efficiently adapt to the changing network topology and match the lower bound, thus proving their optimality. Tight bounds are highly valuable in understanding fundamental limitations and guiding the development of efficient solutions for decentralized optimization in dynamic network environments.

Non-Smooth Convexity

#

Non-smooth convexity presents a unique challenge in optimization due to the absence of a readily available gradient. Traditional gradient-based methods fail, requiring alternative approaches such as subgradient methods. These methods rely on finding a vector from the subdifferential, which is a set of vectors representing all possible gradients at a given point. The analysis of convergence rates becomes more intricate compared to the smooth setting, often requiring additional assumptions such as Lipschitz continuity of the objective function or its subgradients. The trade-off between computational cost and convergence speed needs careful consideration. While non-smooth convex problems are more challenging to solve, many real-world applications, like robust statistics and machine learning, naturally exhibit non-smooth convex structures. Thus, understanding and developing efficient algorithms for this class of problems is crucial. The choice of algorithm will strongly depend on specific characteristics of the objective function and the desired level of accuracy. Despite the inherent complexities, the field actively researches innovative methods to improve efficiency and robustness in handling non-smooth convex optimization.

Saddle-Point Reformulation

#

The saddle-point reformulation is a crucial technique used in optimization to transform a challenging minimization problem into an equivalent saddle-point problem. This reformulation often simplifies the optimization process, particularly for decentralized optimization problems over time-varying networks, which are known for their complexity. The key idea is to introduce dual variables and a suitable Lagrangian to convert the original objective function into a saddle-point function. This reformulation facilitates the application of efficient saddle-point optimization algorithms, such as the Forward-Backward algorithm or its accelerated variants. The resulting saddle-point problem often has superior theoretical properties, making it easier to analyze convergence rates and establish optimality. However, the choice of dual variables and Lagrangian necessitates careful consideration, as it directly impacts the effectiveness of the reformulation. A well-designed saddle-point reformulation must maintain equivalence with the original problem while offering a more manageable structure for optimization. This technique is particularly beneficial when dealing with non-smooth objective functions because it can effectively handle subgradients and the complexities of decentralized computation.

Future Research

#

Future research directions stemming from this work could explore extensions to non-convex settings, acknowledging the inherent challenges in establishing lower bounds and designing optimal algorithms. Investigating the impact of different communication network models beyond time-varying graphs, such as those with dynamic topologies or communication delays, is crucial for practical applicability. A deeper examination of the algorithm’s robustness to noise and data heterogeneity in decentralized settings would enhance its real-world applicability. Finally, empirical validation on large-scale machine learning tasks would solidify the theoretical results and demonstrate the algorithm’s competitiveness against existing methods. The development of distributed algorithms for specific problem classes, such as those arising in federated learning or multi-agent systems, offers opportunities for tailored optimization strategies. Another exciting avenue is incorporating privacy-preserving techniques, allowing for decentralized optimization while protecting sensitive data.

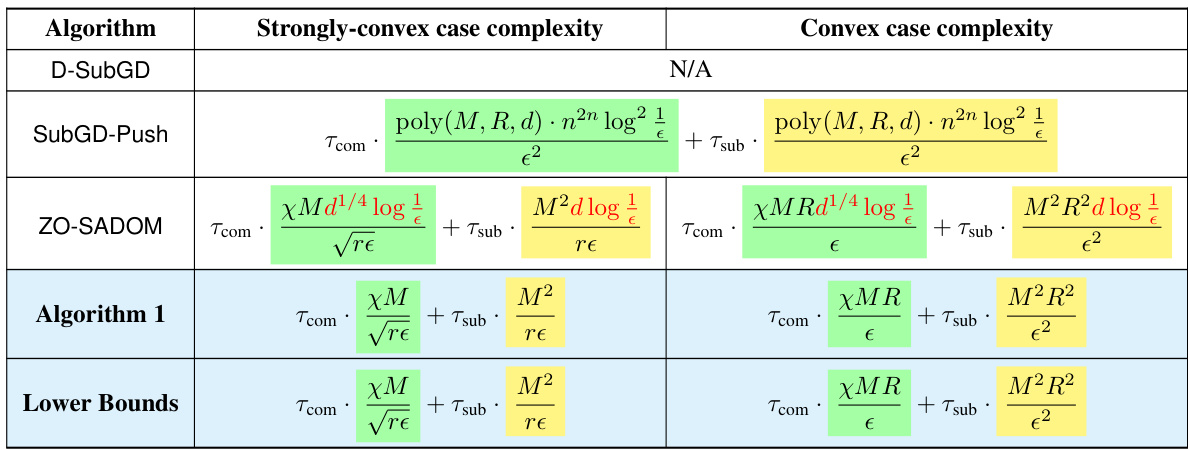
More visual insights

#

More on tables

This table summarizes the state-of-the-art results in decentralized convex optimization, categorized by the smoothness of the objective function and the type of network (fixed or time-varying). It highlights papers that provide lower complexity bounds and those that offer optimal algorithms matching those bounds. The table shows that while optimal algorithms exist for smooth settings, the non-smooth setting with time-varying networks was largely unexplored before this paper.

This table summarizes the state-of-the-art results in decentralized convex optimization, categorized by smoothness of the objective function (smooth vs. non-smooth) and network type (fixed vs. time-varying). It shows which papers established lower bounds on the communication and computation complexity, and which papers presented optimal algorithms that achieved these lower bounds. The table highlights the gap in the literature addressed by the current paper, namely the non-smooth setting with time-varying networks.

Full paper

#