Physics-Informed Regularization for Domain-Agnostic Dynamical System Modeling

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on dynamical systems modeling because it introduces a novel framework, TREAT, that significantly improves modeling accuracy across various systems. TREAT’s broad applicability and its theoretical grounding in minimizing numerical errors during ODE integration make it a valuable tool for various applications. The findings open new avenues for investigating the interplay between physics-informed priors and numerical optimization in achieving more accurate and robust predictions.

Visual Insights

#

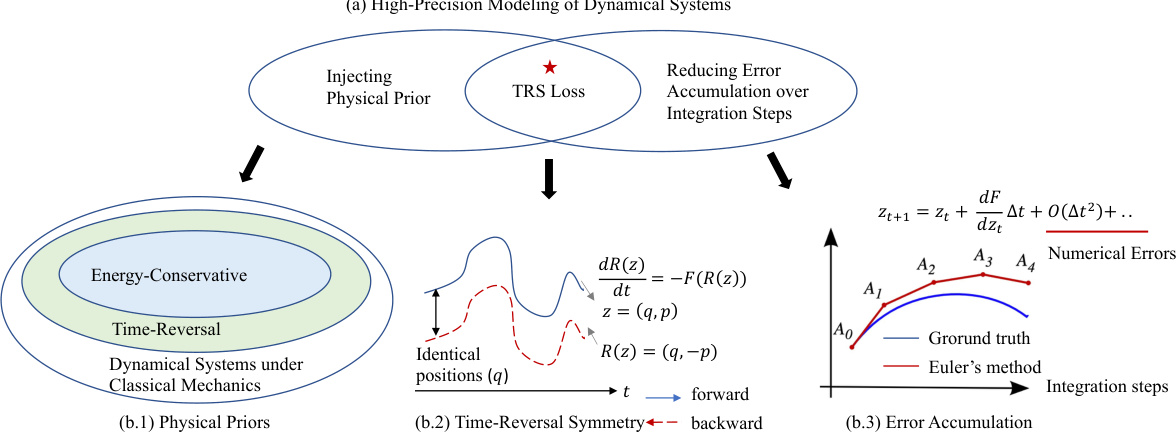
This figure illustrates the core idea of the paper. Panel (a) shows how injecting a physics-informed prior (Time-Reversal Symmetry or TRS) and using a TRS loss reduces error accumulation during the ODE integration process, leading to high-precision modeling. Panels (b.1), (b.2), and (b.3) provide supporting details. (b.1) classifies classical mechanical systems based on whether they are energy-conservative, time-reversible, or both. (b.2) illustrates TRS and how it is used in the model. (b.3) depicts the error accumulation that can occur in numerical ODE solvers, which the paper aims to mitigate.

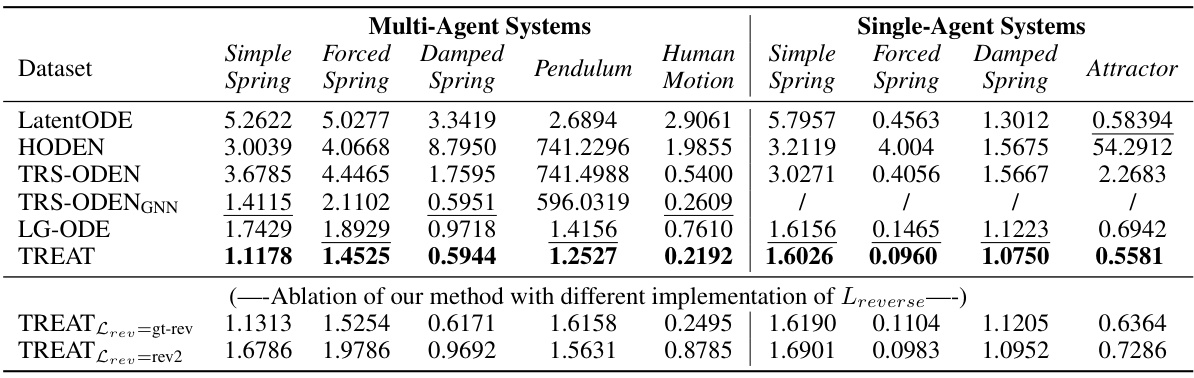
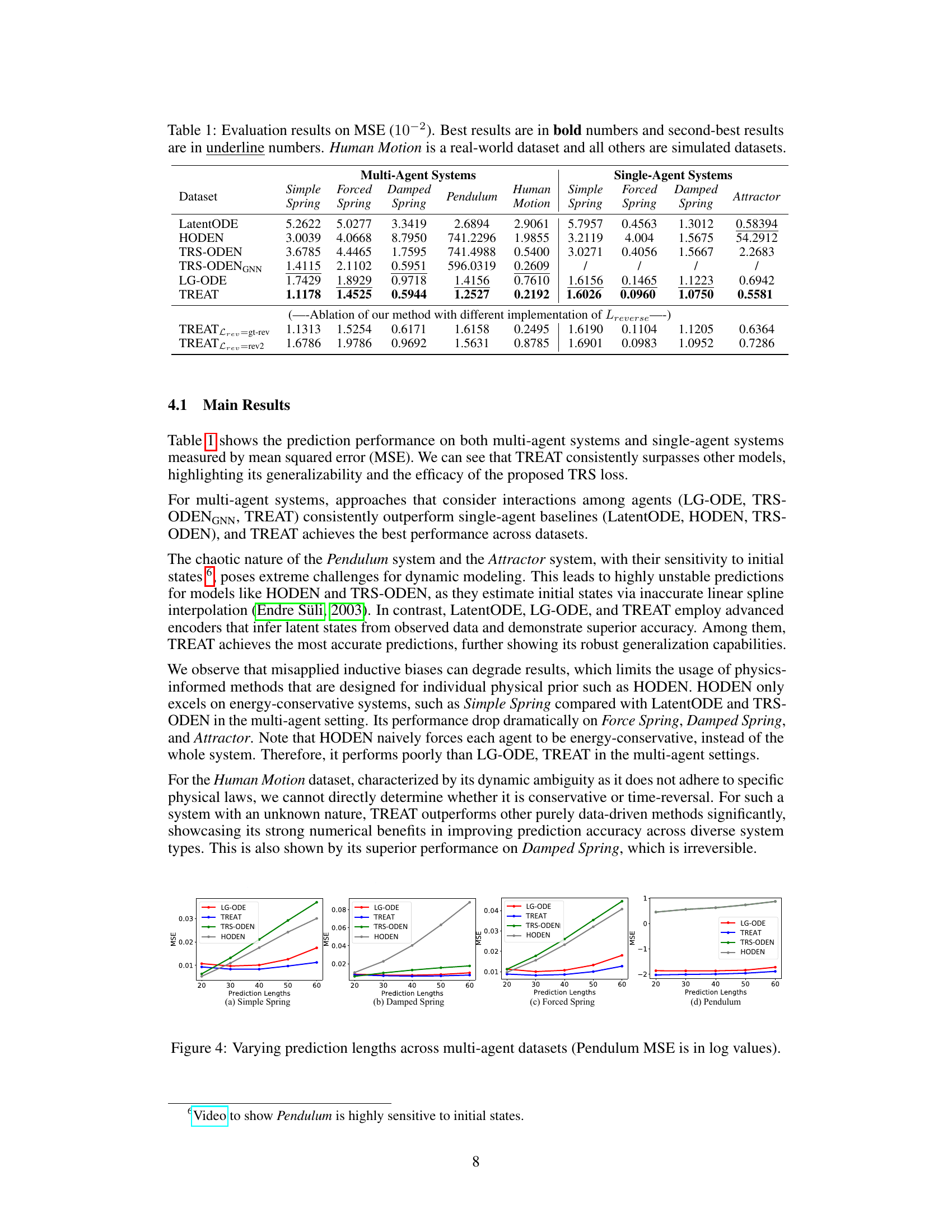
This table presents the Mean Squared Error (MSE) achieved by different models on various datasets, including both multi-agent and single-agent systems. The best and second-best performing models for each dataset are highlighted. The datasets are diverse, including simulated and real-world data, with varying physical properties. The results demonstrate the superiority of the proposed TREAT model across different datasets.

In-depth insights

#

TRS Loss Benefits

#

The theoretical analysis of TRS loss benefits reveals its capacity to enhance the accuracy of dynamical system modeling irrespective of the system’s inherent physical properties. The key insight is that TRS loss minimizes higher-order Taylor expansion terms during ODE integration. This numerical advantage translates to improved precision, particularly beneficial for long-term predictions where error accumulation becomes significant. While TRS is a domain-specific physical prior, the universal improvement in modeling accuracy is demonstrated through a theoretical proof, minimizing Taylor expansion errors. This makes TREAT exceptionally effective across diverse dynamical systems, including those that aren’t strictly energy-conservative or reversible. Furthermore, empirical results validate these findings, highlighting the versatility and robustness of the method. The advantages extend to handling noisy data and irregular sampling, demonstrating the practical significance of TRS loss. In essence, TREAT offers a powerful and generalizable regularization approach for dynamical systems modeling which improves upon existing physics-informed methods by addressing limitations related to specific physical priors.

TREAT Framework

#

The TREAT framework introduces a novel approach to dynamical system modeling by integrating time-reversal symmetry (TRS) as a regularization technique. This method enhances model accuracy by minimizing higher-order Taylor expansion terms during ODE integration, a benefit applicable to diverse systems regardless of their inherent physical properties. TREAT leverages GraphODEs, a neural network architecture well-suited for modeling interacting systems, to predict forward trajectories and, importantly, reverse trajectories. By aligning these forward and reverse predictions using a self-supervised TRS loss, TREAT implicitly enforces consistency and accuracy across time. This framework demonstrates superior performance compared to existing methods, especially in challenging scenarios with limited data or high sensitivity to initial conditions, showcasing its robustness and broad applicability for a wide range of dynamic modeling tasks.

Diverse System Tests

#

A robust evaluation of a dynamical systems model necessitates testing its performance across a wide spectrum of systems. A section titled “Diverse System Tests” would ideally showcase the model’s generalizability and reliability by applying it to scenarios with varying characteristics, including diverse physical laws, levels of complexity (single-agent vs. multi-agent), and data properties (clean vs. noisy, regularly vs. irregularly sampled). The inclusion of both simulated and real-world datasets is crucial for assessing practical applicability. Systematic comparisons to established baselines are essential for demonstrating improvements. The choice of evaluation metrics should align with the practical goals, potentially including metrics evaluating accuracy, robustness, and computational efficiency. Detailed descriptions of each tested system and the reasons for their selection would further enhance the evaluation’s credibility and insightfulness. By carefully designing and presenting diverse system tests, researchers can comprehensively demonstrate the strengths and limitations of their dynamical system modeling approach and identify areas for future improvement.

Ablation Studies

#

Ablation studies systematically remove components of a model to assess their individual contributions. In the context of a physics-informed neural network for dynamical systems, these studies would likely investigate the impact of removing or altering different aspects of the model’s architecture or training process. Key areas for ablation would include the physics-informed regularization term, such as the Time-Reversal Symmetry (TRS) loss. Removing the TRS loss would reveal its effectiveness in improving accuracy and generalization. The ablation could also explore different variants of the physics-informed regularization, comparing their performance and determining the optimal balance between incorporating physical priors and fitting the data. Architectural components like the encoder, the ODE solver, and the decoder could be individually ablated, to gauge the effect of each module on the overall performance. Furthermore, ablation studies could investigate the impact of hyperparameters, examining how the model’s behavior changes under different choices of these parameters. By carefully designing and analyzing ablation experiments, valuable insights can be obtained into the relative importance of different components and the overall effectiveness of the proposed methodology.

Future Directions

#

Future research could explore extending the TREAT framework to handle more complex system dynamics, such as those involving high dimensionality, stochasticity, and non-smooth behavior. Investigating the effectiveness of TREAT on systems with different physical priors beyond those considered in the paper is also crucial. Furthermore, a more in-depth theoretical analysis could provide a deeper understanding of the universal benefits of the time-reversal symmetry constraint. The development of more efficient and scalable algorithms is key for broader applicability, especially when dealing with large-scale dynamical systems. Finally, exploring applications of TREAT in other domains beyond those explored in the paper, such as climate modeling, drug discovery, and robotics is warranted. A key challenge will be adapting TREAT to efficiently handle the unique characteristics and complexities of these diverse application areas.

More visual insights

#

More on figures

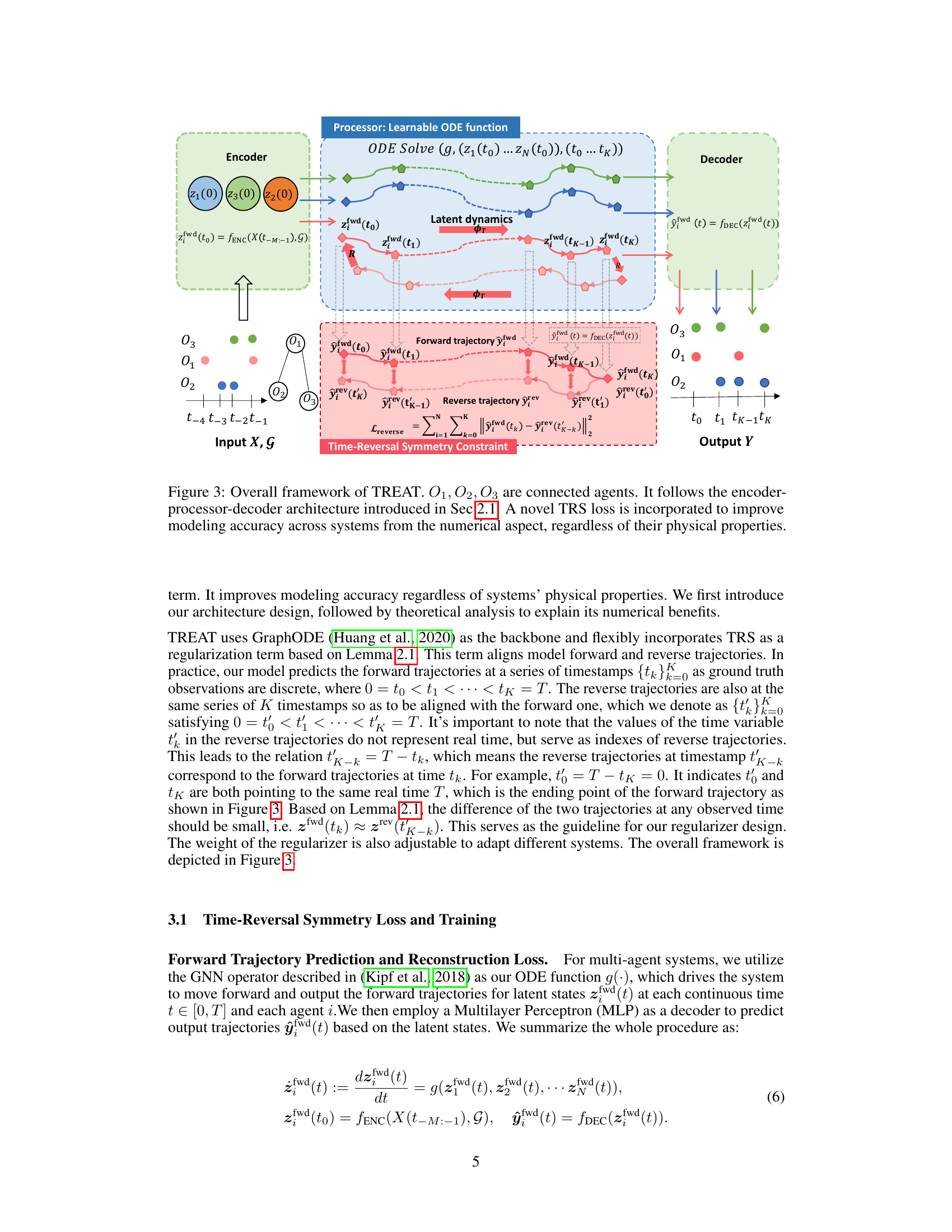
The figure shows the overall framework of the proposed model, TREAT. It illustrates the encoder, processor (learnable ODE function), and decoder components. The key feature highlighted is the incorporation of a novel Time-Reversal Symmetry (TRS) loss to improve the model’s accuracy across diverse dynamical systems. The figure visually depicts how forward and reverse trajectories are aligned using the TRS constraint. This method aims to improve numerical accuracy regardless of the underlying physical properties of the system.

This figure illustrates the overall framework of the TREAT model, which is based on a Graph Neural Ordinary Differential Equation (GraphODE) architecture. The model takes as input a graph G representing the interactions between agents and their historical trajectories X. An encoder processes this input to compute latent initial states for each agent. A learnable ODE function then evolves these latent states over time, producing latent dynamics. A novel Time-Reversal Symmetry (TRS) loss is incorporated to constrain the forward and reverse trajectories of the system. A decoder finally maps the latent states to predicted output trajectories Y.

This figure shows the Mean Squared Error (MSE) for different prediction lengths across four multi-agent datasets: Simple Spring, Damped Spring, Forced Spring, and Pendulum. The x-axis represents the prediction length, and the y-axis represents the MSE. The Pendulum dataset’s MSE is shown on a logarithmic scale due to its significantly higher values. The plot displays the performance of four different models: LG-ODE, TREAT, TRS-ODEN, and HODEN. The purpose is to demonstrate how the prediction accuracy changes for each model as the prediction length increases, highlighting the model’s ability to make accurate predictions over long time horizons. TREAT consistently exhibits the lowest MSE across all datasets and prediction lengths.

This figure shows the mean squared error (MSE) for different prediction lengths across four multi-agent datasets: Simple Spring, Damped Spring, Forced Spring, and Pendulum. The x-axis represents the prediction length, and the y-axis represents the MSE. The figure demonstrates that TREAT consistently outperforms other models, especially as prediction length increases. The Pendulum dataset shows a particularly significant performance improvement by TREAT, which is highlighted by the use of a logarithmic scale for the y-axis in that plot.

This figure shows the overall framework of the proposed method TREAT. It uses a GraphODE model with an encoder, processor (learnable ODE function), and decoder. A key innovation is the inclusion of a novel Time-Reversal Symmetry (TRS) loss to regularize the model and improve accuracy. The figure illustrates how the model processes input data (X, G) to produce output trajectories (Y), showcasing the forward and reverse trajectories in the latent space.

This figure shows how the mean squared error (MSE) changes with prediction length for four different multi-agent datasets: Simple Spring, Damped Spring, Forced Spring, and Pendulum. Each plot displays the MSE for two different models, LG-ODE and TREAT, across varying prediction lengths. The plots show that TREAT generally maintains significantly lower MSE values than LG-ODE, and that the performance gap widens as prediction length increases. The Pendulum dataset’s MSE is plotted on a logarithmic scale due to its high values.

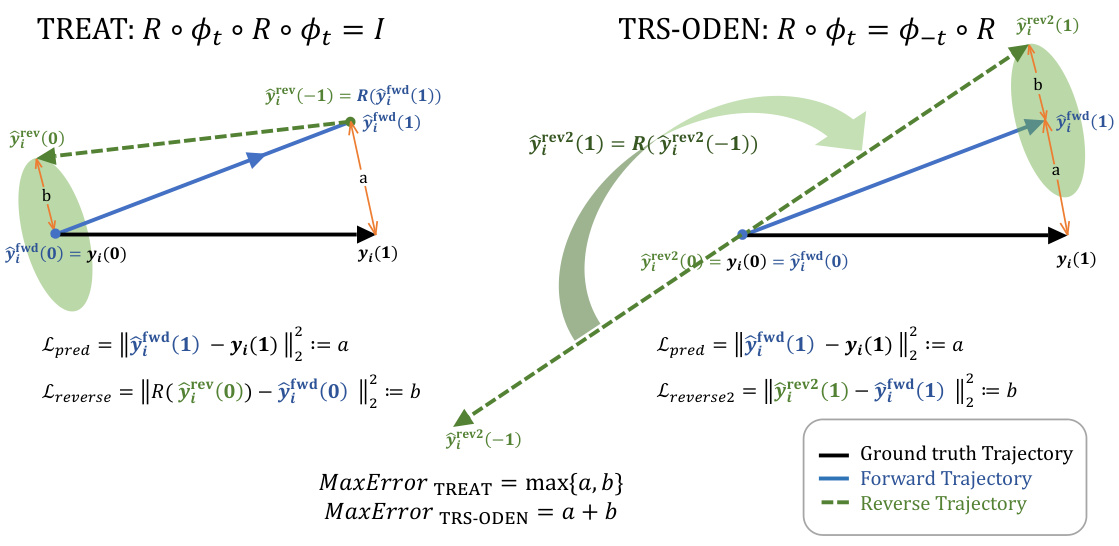
This figure compares two different implementations of the time-reversal symmetry loss: TREAT’s approach based on Lemma 2.1 and TRS-ODEN’s approach based on Equation 5. It illustrates how TREAT’s method minimizes the maximum error between the reversed and ground truth trajectories by independently assessing the forward and reverse loss values, while TRS-ODEN’s method risks accumulating errors, leading to potentially larger errors.

The figure shows the trajectories of a chaotic triple pendulum system with different initial conditions. Even small perturbations in the initial state (Θ₀) lead to significantly different trajectories over time, highlighting the system’s sensitivity to initial conditions and its chaotic nature. This sensitivity poses a challenge for accurate modeling and prediction using machine learning methods.

More on tables

This table presents the Mean Squared Error (MSE) results for various dynamical systems, comparing the performance of TREAT against several baseline methods. The results are categorized by dataset type (single agent vs. multi-agent) and whether the dataset is simulated or from real-world data (Human Motion). Lower MSE values indicate better performance.

This table presents the mean squared error (MSE) results for different multi-agent systems using two different ODE solvers: Euler and Runge-Kutta (RK4). It compares the performance of LGODE and TREAT across the different systems and solvers, showing the improvement achieved by TREAT. The improvement percentage is calculated for each system/solver combination.

This table shows the mean squared error (MSE) achieved by LG-ODE and TREAT models on four multi-agent datasets (Simple Spring, Forced Spring, Damped Spring, and Pendulum) under different observation ratios (0.8 and 0.4). The observation ratio represents the percentage of historical observations used for prediction. The results demonstrate TREAT’s robustness to data sparsity, showing smaller performance degradation than LG-ODE when the observation ratio decreases from 0.8 to 0.4, particularly on the more complex Pendulum dataset.

Full paper

#