TL;DR#
Distributed machine learning faces challenges in balancing privacy, scalability, and training efficiency across heterogeneous agents. Existing analyses often focus on the worst-performing agent, neglecting the potential contributions of better-performing ones. This paper investigates Unified Distributed SGD (UD-SGD), examining various communication patterns and sampling strategies. The key issue is how individual agent dynamics influence the algorithm’s overall performance.
This research uses asymptotic analysis to study UD-SGD’s convergence under different sampling methods (i.i.d., shuffling, Markovian). The findings reveal that efficient sampling strategies significantly contribute to overall convergence, supporting existing theories. Importantly, simulations demonstrate that a few agents using highly efficient sampling can achieve or surpass the performance of the majority, offering insights beyond traditional worst-case analyses. This highlights the importance of understanding and managing individual agent dynamics in distributed learning systems.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers a novel asymptotic analysis of Unified Distributed SGD (UD-SGD), a widely used algorithm in distributed machine learning. It moves beyond traditional analyses by showing how efficient sampling strategies by individual agents significantly impact overall convergence, opening new avenues for optimization and understanding agent dynamics in large-scale systems. The empirical results underscore that a few high-performing agents can substantially improve overall results, highlighting the importance of diverse agent capabilities rather than focusing only on the worst-performing agent.
Visual Insights#
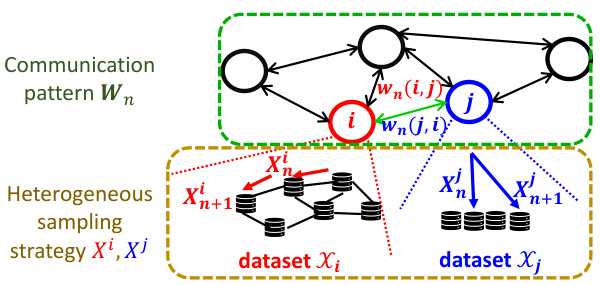
🔼 This figure illustrates the Unified Distributed SGD (UD-SGD) algorithm with various communication patterns and sampling strategies. It shows a communication network of 5 agents (nodes), each holding potentially different datasets. Agent dynamics are visualized, showing how agent j samples data independently and identically distributed (i.i.d.), while agent i samples data according to a Markovian trajectory. Different communication patterns (represented by the matrix Wn) are also depicted. The figure highlights the heterogeneous nature of sampling strategies across agents, and how they affect the convergence of the UD-SGD algorithm.
read the caption
Figure 1: GD-SGD algorithm with a communication network of N = 5 agents, each holding potentially distinct datasets; e.g., agent j (in blue) samples Xj i.i.d. and agent i (in red) samples Xi via Markovian trajectory.
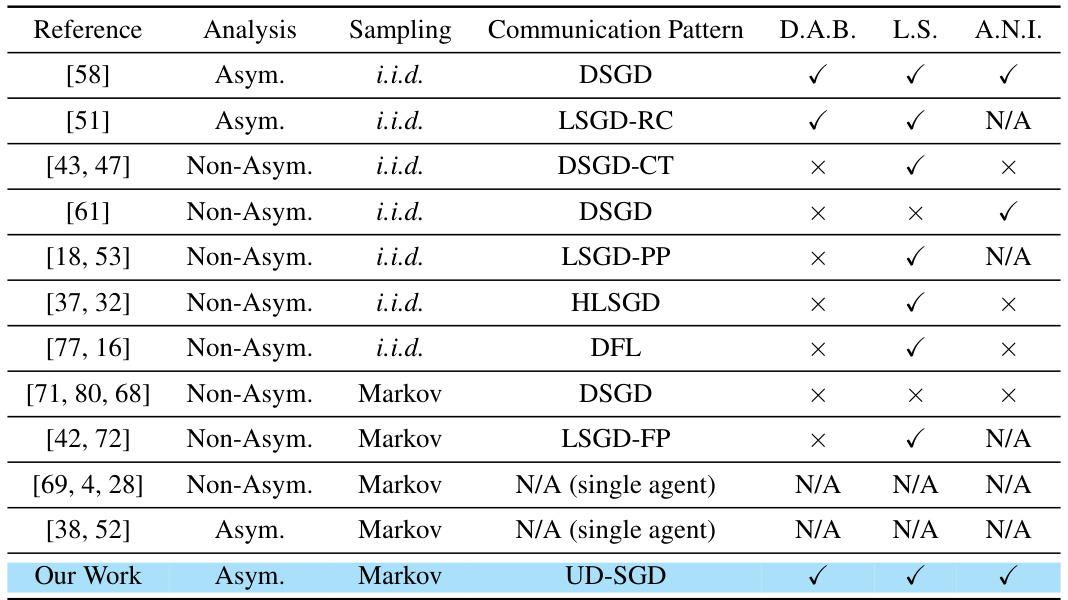
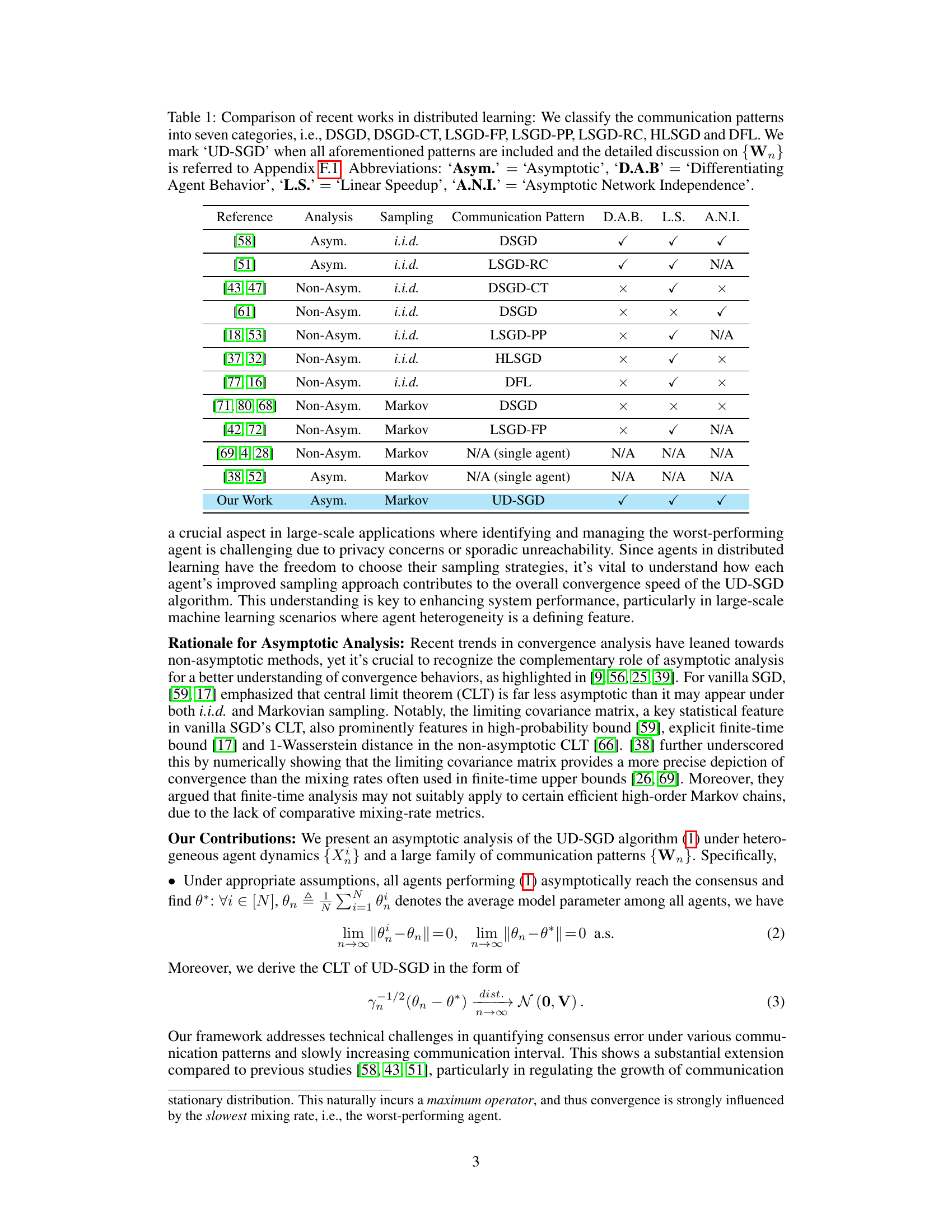
🔼 This table compares existing works in distributed learning, focusing on their analysis type (asymptotic or non-asymptotic), sampling method (i.i.d. or Markov), communication pattern, and whether they differentiate agent behavior, achieve linear speedup, and demonstrate asymptotic network independence. It highlights the novelty of the current work in considering a unified distributed setting, Markovian sampling, and differentiating agent behavior.
read the caption
Table 1: Comparison of recent works in distributed learning: We classify the communication patterns into seven categories, i.e., DSGD, DSGD-CT, LSGD-FP, LSGD-PP, LSGD-RC, HLSGD and DFL. We mark ‘UD-SGD’ when all aforementioned patterns are included and the detailed discussion on {Wn} is referred to Appendix F.1. Abbreviations: ‘Asym.’ = ‘Asymptotic’, ‘D.A.B’ = ‘Differentiating Agent Behavior’, ‘L.S.’ = ‘Linear Speedup’, ‘A.N.I.’ = ‘Asymptotic Network Independence’.
In-depth insights#
UD-SGD Dynamics#
Analyzing UD-SGD dynamics reveals crucial insights into distributed learning. The framework’s versatility allows exploration of various communication patterns (decentralized SGD, local SGD within Federated Learning), highlighting the impact of agent dynamics and sampling strategies. The asymptotic analysis, using the Central Limit Theorem, provides theoretical support for linear speedup and network independence, but also demonstrates the influence of individual agents’ sampling efficiency on overall convergence. Efficient sampling strategies by a few agents can significantly enhance overall performance, surpassing the performance of a majority using moderate strategies, a finding beyond traditional analyses focusing solely on the worst-performing agent. This research shifts the focus from the laggard to the collective effect of heterogeneous agent dynamics, offering valuable implications for large-scale distributed learning system design and optimization.
Sampling Strategies#
The paper thoroughly investigates various sampling strategies, particularly focusing on their impact on the convergence of Unified Distributed SGD (UD-SGD). It highlights the differences between i.i.d. sampling, shuffling, and Markovian sampling, demonstrating how the choice of sampling strategy affects the convergence speed and overall performance. The authors theoretically and empirically show that efficient sampling, such as those using Markovian chains with faster mixing rates, significantly contributes to the overall convergence, even when only a subset of agents adopt them. This contrasts with traditional analyses that focus solely on the worst-performing agent. The study’s asymptotic analysis, based on the Central Limit Theorem, provides valuable insights into the impact of each agent’s sampling strategy on the final limiting covariance matrix, a key statistical feature that captures the efficiency of sampling. This approach allows a detailed assessment of the combined impact of the various agent strategies, thereby offering a more nuanced perspective on the convergence behavior of UD-SGD than previously available. The paper’s key takeaway emphasizes that focusing on enhancing the efficiency of sampling for even a small number of agents can drastically improve the overall system performance, a finding that has crucial implications for large-scale and heterogeneous distributed learning systems.
Asymptotic Analysis#
The ‘Asymptotic Analysis’ section of this research paper delves into the long-term behavior of the Unified Distributed Stochastic Gradient Descent (UD-SGD) algorithm. It uses the Central Limit Theorem (CLT) to characterize the convergence of the algorithm under various communication patterns and heterogeneous agent dynamics, focusing on the asymptotic properties rather than finite-time behavior. This approach is particularly valuable for understanding the impact of different sampling strategies on the overall convergence. The CLT provides insights into the limiting distribution of the model parameters, which allows for a quantitative evaluation of the efficiency of each agent’s sampling and communication. This contrasts with many existing non-asymptotic analyses that primarily focus on the worst-performing agent. The study’s asymptotic analysis also supports existing theories on linear speedup and network independence, providing theoretical backing for empirical observations. In essence, this section provides a rigorous mathematical framework for understanding how diverse factors influence the long-term convergence of UD-SGD, offering a more holistic analysis compared to traditional finite-time analyses.
Agent Heterogeneity#
Agent heterogeneity is a crucial factor influencing the performance of distributed learning algorithms. Differences in data distribution, computational resources, and communication capabilities among agents create challenges for achieving consensus and efficient model training. The paper explores various sampling strategies to mitigate these issues, acknowledging that a few high-performing agents can significantly impact overall convergence. Strategies like Markovian sampling, which can model more realistic data access patterns in federated learning, are highlighted. The impact of agent heterogeneity is not limited to the worst-performing agent; a balanced analysis needs to consider the combined effect of all agents, including both high and low-performing ones. This necessitates a move beyond traditional analyses focusing solely on the worst-case scenario and highlights the importance of understanding how individual agent dynamics contribute to system-wide convergence.
Future Research#
Future research directions stemming from this work could focus on tightening the finite-sample bounds of the UD-SGD algorithm to offer a more precise characterization of agent dynamics. Currently, the analysis relies heavily on asymptotic behavior, which may not completely capture finite-time performance. Further investigation into non-asymptotic convergence analysis under heterogeneous agent dynamics and various communication patterns is needed. Another promising area lies in exploring different sampling strategies, such as those employing non-linear Markov chains or adaptive sampling methods that dynamically adjust to the data distribution and agent capabilities. Relaxing assumptions such as the almost sure boundedness of model parameters is also important. Finally, empirical evaluation on a wider array of real-world datasets and applications will be crucial to validate and extend the insights gained from this research.
More visual insights#
More on figures
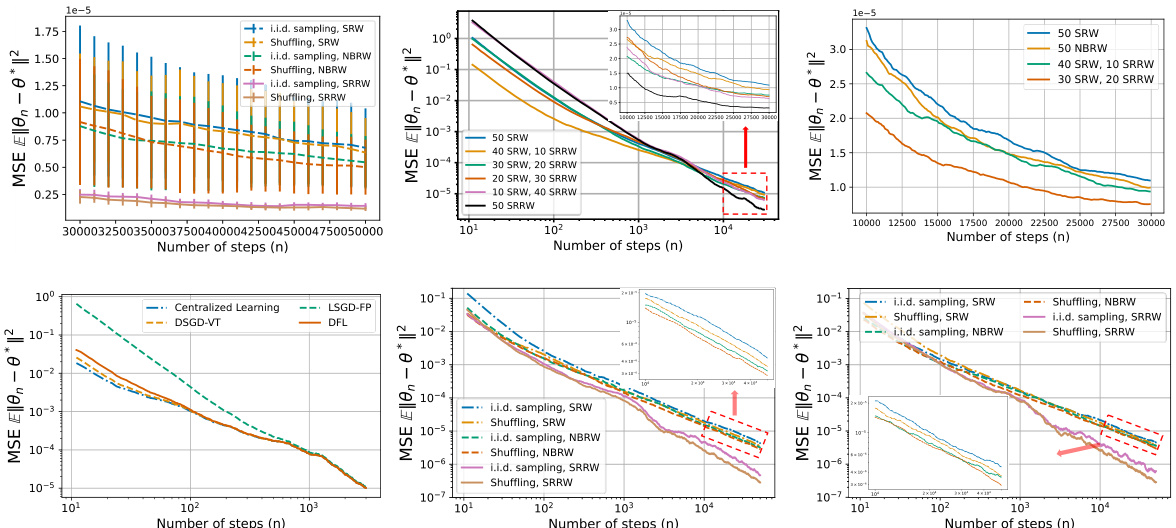
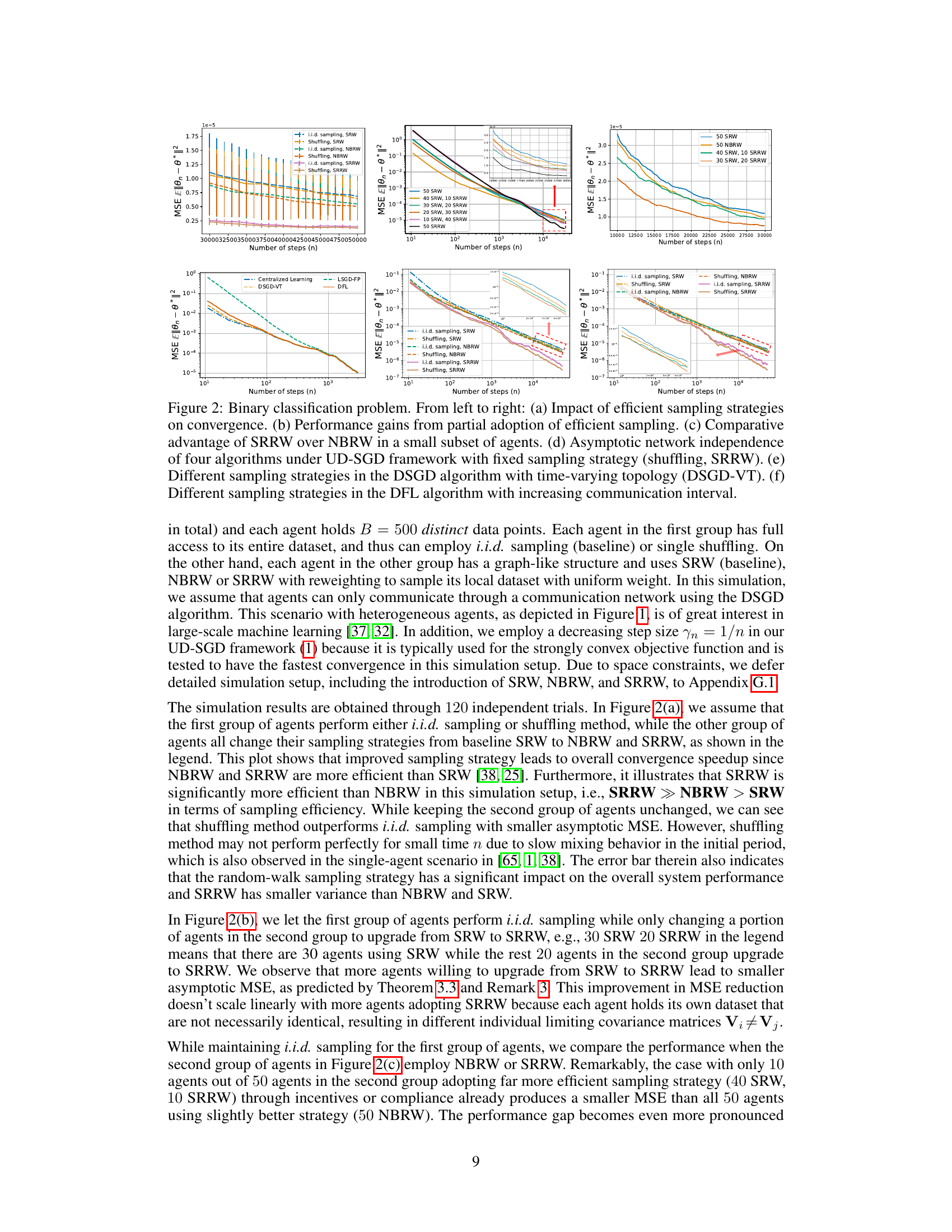
🔼 This figure shows the impact of different sampling strategies on the convergence speed of the UD-SGD algorithm in a binary classification task. Panel (a) compares the convergence with different sampling strategies (i.i.d., shuffling, SRW, NBRW, SRRW). Panel (b) demonstrates the improvement when only a portion of agents uses more efficient sampling strategies. Panel (c) highlights the superiority of SRRW over NBRW even when only a small number of agents use it. Panel (d) illustrates the asymptotic network independence of different algorithms under UD-SGD. Panels (e) and (f) compare the performance of various algorithms with different communication patterns.
read the caption
Figure 2: Binary classification problem. From left to right: (a) Impact of efficient sampling strategies on convergence. (b) Performance gains from partial adoption of efficient sampling. (c) Comparative advantage of SRRW over NBRW in a small subset of agents. (d) Asymptotic network independence of four algorithms under UD-SGD framework with fixed sampling strategy (shuffling, SRRW). (e) Different sampling strategies in the DSGD algorithm with time-varying topology (DSGD-VT). (f) Different sampling strategies in the DFL algorithm with increasing communication interval.

🔼 This figure shows the impact of different sampling strategies on the convergence of UD-SGD under various communication patterns. Panel (a) compares the convergence speed of different sampling methods (i.i.d., shuffling, SRW, NBRW, SRRW) across different algorithms. Panel (b) illustrates the performance improvement when only a subset of agents employ a more efficient sampling strategy. Panel (c) shows the superior performance of SRRW compared to NBRW. Panel (d) demonstrates the asymptotic network independence of different algorithms under UD-SGD with shuffling and SRRW sampling. Panels (e) and (f) examine the impact of different sampling strategies on the DSGD-VT and DFL algorithms, respectively.
read the caption
Figure 2: Binary classification problem. From left to right: (a) Impact of efficient sampling strategies on convergence. (b) Performance gains from partial adoption of efficient sampling. (c) Comparative advantage of SRRW over NBRW in a small subset of agents. (d) Asymptotic network independence of four algorithms under UD-SGD framework with fixed sampling strategy (shuffling, SRRW). (e) Different sampling strategies in the DSGD algorithm with time-varying topology (DSGD-VT). (f) Different sampling strategies in the DFL algorithm with increasing communication interval.
Full paper#