↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world datasets, like videos, exhibit complex temporal dynamics and nonstationary shifts, hindering the accurate identification of causal relationships. Existing methods often rely on strong assumptions (directly observing domain variables or assuming a Markov property), limiting their applicability. This paper addresses this by presenting a novel method that relies on a sparse transition assumption, which is more aligned with how humans intuitively understand such phenomena.
The paper introduces a new framework, CtrlNS, that leverages sparsity and conditional independence to identify both distribution shifts (domain variables) and latent factors. The approach is theoretically grounded, offering identifiability results, and demonstrates significant improvements over state-of-the-art methods across synthetic and real-world datasets (such as video action segmentation). The success of CtrlNS highlights the effectiveness of the sparse transition assumption for modeling nonstationary time series and showcases its potential for various applications dealing with sequential data.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with nonstationary time-series data, a prevalent challenge across many fields. It offers a novel framework and theoretical foundation for causal learning in such settings, going beyond existing limitations of requiring directly observed variables or Markov assumptions. The proposed method, CtrlNS, demonstrates superior performance on both synthetic and real-world datasets, opening avenues for applications such as video action segmentation and other sequential data analysis tasks.
Visual Insights#
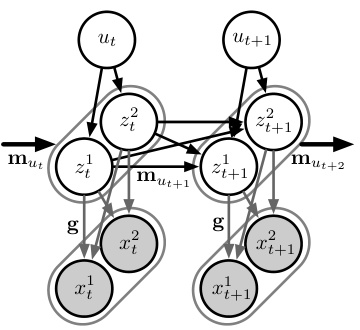
This figure shows a graphical model illustrating the generation process of nonstationary time-series data. The model incorporates time-delayed causal relationships between latent variables (z), unobserved domain variables (u) that influence transition functions (m), and observed variables (x). The arrows represent the causal relationships. The mixing function ‘g’ maps the latent variables to the observed variables. The model highlights the nonstationary nature of the transitions, reflecting the varying relationships over time, influenced by the domain variables.
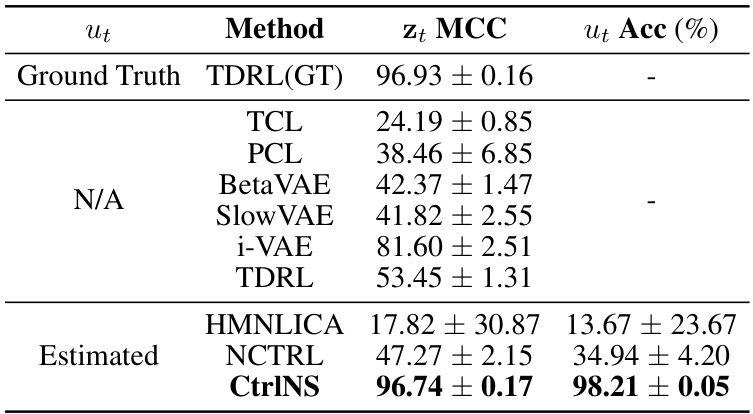
This table presents the quantitative results of experiments conducted on synthetic datasets to evaluate the performance of the proposed CtrlNS model and compare it against several baseline methods. The metrics used are MCC (Mean Correlation Coefficient) for evaluating the identifiability of latent variables (zt) and Acc (Accuracy) for evaluating the identifiability of domain variables (ut). The results show that CtrlNS significantly outperforms all the baseline methods in terms of both MCC and Acc, indicating its superior ability in recovering both latent and domain variables in nonstationary settings.
In-depth insights#
Nonstationary Ctrl#
Nonstationary causal temporal representation learning (Ctrl) tackles the challenge of identifying temporal causal relationships in dynamic systems where the underlying causal mechanisms change over time. Standard Ctrl methods often assume stationarity, meaning the causal processes remain constant. However, real-world data frequently exhibits nonstationarity, leading to inaccurate or unreliable causal inferences if stationarity is assumed. Nonstationary Ctrl addresses this limitation by explicitly modeling and accounting for these changes. This might involve techniques such as incorporating time-varying parameters, segmenting data into stationary regimes, or using flexible models capable of capturing shifts in distribution. Successfully addressing nonstationarity is crucial for building robust and reliable causal models in applications such as video analysis, where causal relationships shift dramatically between different scenes or actions. Identifiability — the ability to uniquely determine the underlying causal structure from observed data— becomes a critical theoretical concern when dealing with nonstationarity, and robust methods must address this to guarantee the reliability of causal discovery. In essence, Nonstationary Ctrl represents a significant advancement over stationary approaches, enabling more accurate and nuanced causal understanding in complex, real-world systems.
Sparse Transition#
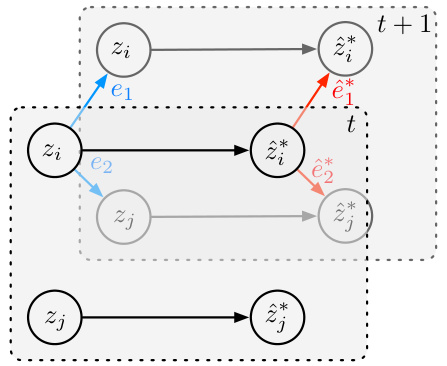
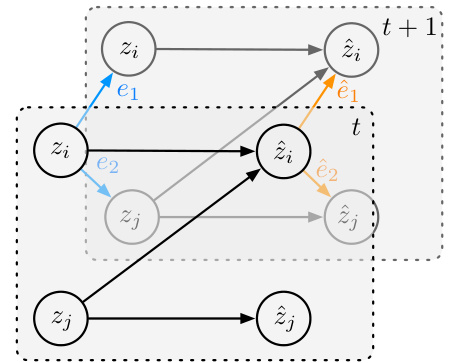
The concept of ‘Sparse Transition’ in the context of causal temporal representation learning suggests that changes in the underlying latent variables are not uniformly distributed across all possible transitions. Instead, most transitions leave many latent components unchanged, focusing changes on a smaller subset of components. This sparsity assumption is crucial for identifiability and model efficiency. It implies that the model should not need to explicitly learn and represent every possible transition; rather, it can focus on learning the significant, non-sparse transitions, which are assumed to be more informative. The theoretical implications of sparse transitions are significant, potentially leading to more robust and interpretable models, especially when dealing with high-dimensional data or complex temporal dynamics. However, the success of this approach relies heavily on the validity of the sparsity assumption and may necessitate careful consideration of the problem domain. Empirically, the sparse transition model would benefit from an efficient algorithmic approach capable of identifying and prioritizing the important transitions, separating them from the less-informative sparse transitions. This assumption is particularly useful in the context of non-stationary environments as it allows modeling the changes in causal structure between domains more effectively. The main advantages are improved identifiability of both latent factors and domain variables, as well as enhanced model efficiency and interpretability.
Identifiability Theory#
The heading ‘Identifiability Theory’ suggests a section dedicated to establishing conditions under which causal relationships within a model can be uniquely determined from observed data. This is crucial because multiple models might explain the same observed data, making it impossible to definitively choose the correct causal structure. The theory likely involves proving that under specific assumptions (e.g., on data distribution, model structure, or the presence of specific types of noise), a unique causal model can be identified. This might include demonstrating that different causal structures generate distinct probability distributions of observed data, ensuring identifiability. Key aspects of this section would likely be the definition of identifiability (in the context of the paper’s problem), the statement of assumptions necessary for identifiability, and the rigorous mathematical proof of the identifiability results. The authors likely focus on establishing sufficient conditions, meaning if those conditions hold, then identifiability is guaranteed, but the conditions might not be necessary. This section is vital for assuring the reliability and validity of the paper’s proposed causal inference approach. Mathematical rigor and detailed proofs would underpin the arguments in this section, providing the foundation for confidence in the model’s ability to correctly infer causal relationships.
CtrlNS Framework#
The CtrlNS framework, proposed for causal temporal representation learning with nonstationary sparse transitions, presents a novel approach to tackle the challenges of identifying temporal causal dynamics in complex, real-world scenarios. Its core innovation lies in leveraging the sparsity of transitions and conditional independence assumptions to reliably identify both distribution shifts and latent factors, circumventing the limitations of existing methods that require either direct observation of domain variables or strong Markov assumptions. The framework integrates these constraints within a variational autoencoder (VAE) architecture, where a sparse transition module estimates the transition functions and domain variables, a prior network models the latent variable distributions, and an encoder-decoder ensures the invertibility of the learned mixing function. This integrated design allows for a principled and efficient recovery of both latent dynamics and unobserved domain shifts, showcasing significant improvements over existing baselines in experimental evaluations. The theoretical identifiability results underpinning CtrlNS provide a strong foundation for its effectiveness, highlighting the conditions under which the model’s assumptions guarantee the identification of the underlying causal processes. This work thus offers a robust and powerful solution for causal learning in nonstationary temporal data, particularly in scenarios with limited prior knowledge about the data-generating mechanism.
Future Directions#
Future research could explore several promising avenues. Extending the framework to handle more complex causal relationships beyond the current time-delayed structure is crucial for broader applicability. This includes investigating higher-order dependencies and non-linear interactions within the latent processes. Addressing scenarios with non-stationary transitions that do not exhibit changes in the underlying causal graph but vary in transition functions remains an important challenge. Developing more robust techniques for estimating the transition complexities could improve accuracy and efficiency. Exploring methods to integrate external knowledge or side information, such as domain labels or expert annotations, could boost the model’s performance in scenarios with limited data or ambiguous signals. Finally, applying this theoretical framework to diverse real-world applications, beyond video action segmentation, such as healthcare or finance, will reveal its true potential and limitations, which could lead to further model refinement and extension.
More visual insights#
More on figures
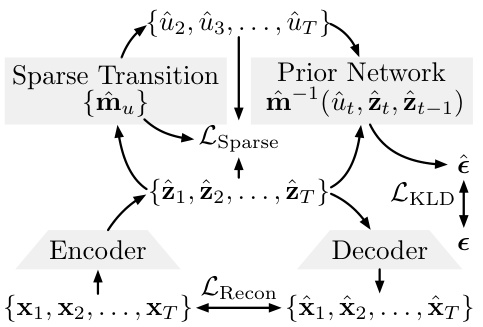
This figure illustrates the architecture of the CtrlNS framework, which consists of three main components: The Sparse Transition module estimates the transition functions and a clustering function to identify domain shifts. The Prior Network estimates the prior distribution of latent variables, ensuring conditional independence. The Encoder-Decoder module uses reconstruction loss to ensure the invertibility of the learned mixing function. These components work together to recover both nonstationary domain variables and time-delayed latent causal dynamics.
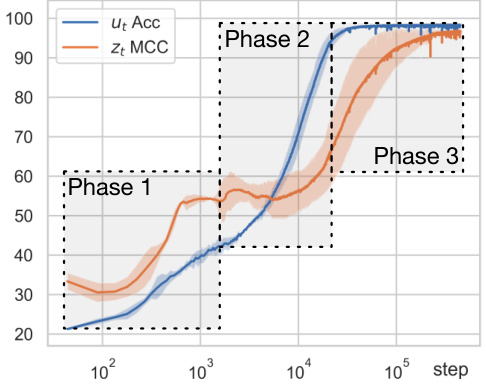
This figure visualizes the training process of the CtrlNS model, which is divided into three phases. Phase 1 shows the initial estimations of both domain variables (ut) and latent variables (zt) are imprecise. During Phase 2, the accuracy of ut estimation improves significantly, while zt estimation remains relatively unchanged. In Phase 3, as ut becomes clearly identifiable, zt estimation accuracy improves substantially, achieving full identifiability. This three-phase behavior supports the theoretical predictions of the paper.

This figure shows two examples of action segmentation results from the Hollywood dataset. Each example shows several frames from a video along with a bar graph visualization for both ground truth and model predictions (ATBA and CtrlNS). The bar graphs represent different action classes through color-coding. The purpose is to visually demonstrate the improvement in action segmentation accuracy achieved by the proposed CtrlNS method compared to the ATBA baseline. The differences in color-coding between the ground truth and model predictions highlight areas where the CtrlNS model provides more accurate segmentation.

This figure shows a graphical model representing the generative process for nonstationary, causally related, time-delayed time series data. The model incorporates unobserved domain variables (ut) that influence the transitions between time-delayed latent components (zt). These latent components then generate the observed data (xt) through a mixing function (g). The model explicitly addresses the nonstationarity by allowing the transition functions (m) to vary depending on the domain variables. This variation in transition functions is key to modeling the distribution shifts inherent to nonstationary data.
This figure is a graphical model illustrating how the observed data (xt) are generated from causally related latent temporal processes (zt) that exhibit nonstationary behavior. The latent variables (zt) are influenced by their previous states (zt-1) and unobserved domain variables (ut) which represent different regimes or domains. The domain variables (ut) determine the transition functions (mt) which govern the changes in the latent variables over time. The observed data (xt) are generated by an invertible mixing function g(zt) which maps the latent variables to the observations. This model captures the time-delayed causal relationships and nonstationary transitions in the data generation process.
This figure illustrates the graphical model used in the paper to represent the nonstationary time series generative model. The model shows how observed variables (xt) are generated from causally related, time-delayed latent components (zt) through an invertible mixing function (g). The latent variables (zt) are generated by transition functions (m), which vary across different domains (ut), which are themselves unobserved. Each latent variable at time t has latent parents from time t-1 (zt-1) which can influence the generation of the variable. Noise terms are also included in the model (et). The figure depicts the causal relationships between these variables.
This figure presents a graphical model illustrating the generative process of nonstationary, causally related, time-delayed time series data. The model incorporates unobserved domain variables (ut) influencing the transitions between time-delayed latent variables (zt). These latent variables then map to the observed variables (xt) through an invertible mixing function. The model depicts the nonstationary nature of the data generation by showing how transitions in the latent space vary across different domains. The time delay is shown by the dependence of Zt on Zt-1.
More on tables
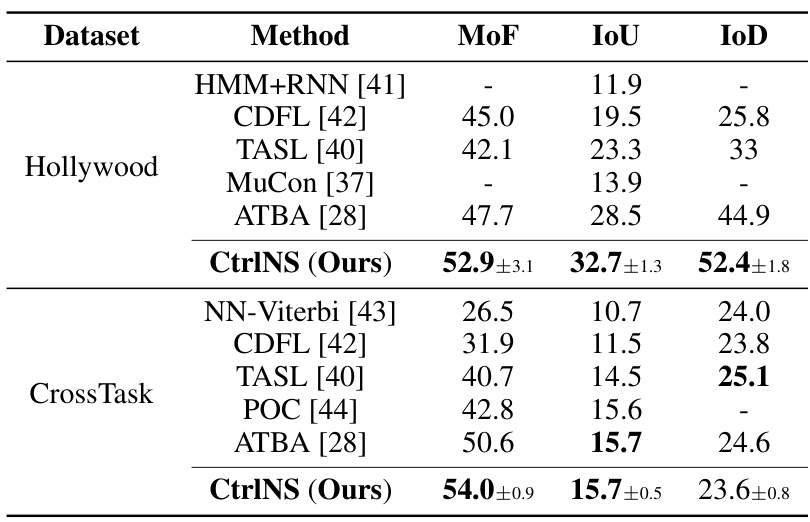
This table presents the quantitative results of the proposed CtrlNS model and several baseline models on a synthetic dataset. The results are presented in terms of the mean correlation coefficient (MCC) for latent variable recovery and clustering accuracy (Acc) for domain variable identification. The table compares the performance of CtrlNS against these baselines, highlighting the superior performance of CtrlNS, particularly in the accuracy of both domain and latent variable identification.
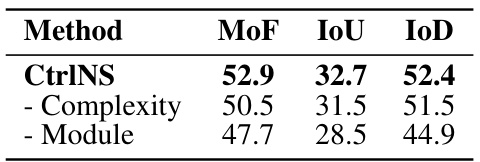
This table presents the quantitative results of the proposed CtrlNS model and several baseline models on a synthetic dataset. The results evaluate the identifiability of the models by comparing the estimated latent variables (MCC) and domain variables (Acc). The CtrlNS model significantly outperforms the baselines in both metrics, demonstrating the effectiveness of its approach.
This table compares the performance of the proposed CtrlNS model against several baseline models on a synthetic dataset. The metrics used are the accuracy of domain variable estimation (Ut Acc) and the mean correlation coefficient (Zt MCC) between estimated and ground truth latent variables. The results show that CtrlNS significantly outperforms the baselines in both metrics, demonstrating its effectiveness.
Full paper#



















