↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Out-of-distribution (OOD) detection in graph data is crucial for reliable graph-based machine learning systems. However, existing techniques often fall short due to their inability to handle the interconnected nature of graphs, resulting in reduced effectiveness. Conventional OOD detection methods, successful in other domains, struggle when applied to graphs because they ignore the graph’s structural information.
The proposed GRASP method tackles this challenge by introducing an innovative edge augmentation strategy combined with score propagation. This post-hoc solution enhances the performance of existing OOD detection functions by strategically adding edges to a subset of the training data. This augmentation increases the ratio of intra-edges, provably improving the accuracy of OOD detection. Extensive experiments show GRASP surpasses existing baselines and reduces error rates significantly.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on out-of-distribution (OOD) detection in graph neural networks. It addresses a significant gap in current research by developing a novel method that leverages score propagation, improving OOD detection accuracy and offering theoretical guarantees. This work offers new avenues for further investigation in graph augmentation and OOD detection strategies, significantly impacting the robustness and reliability of graph-based machine learning systems.
Visual Insights#

This figure illustrates the concept of OOD (Out-of-Distribution) score propagation in a graph. Raw OOD scores are initially assigned to nodes. Then, these scores are propagated to neighboring nodes, influencing their scores. The propagation is shown to occur iteratively, resulting in a refined OOD score for each node after multiple propagation steps. The process aims to leverage the graph structure for enhanced OOD detection accuracy.
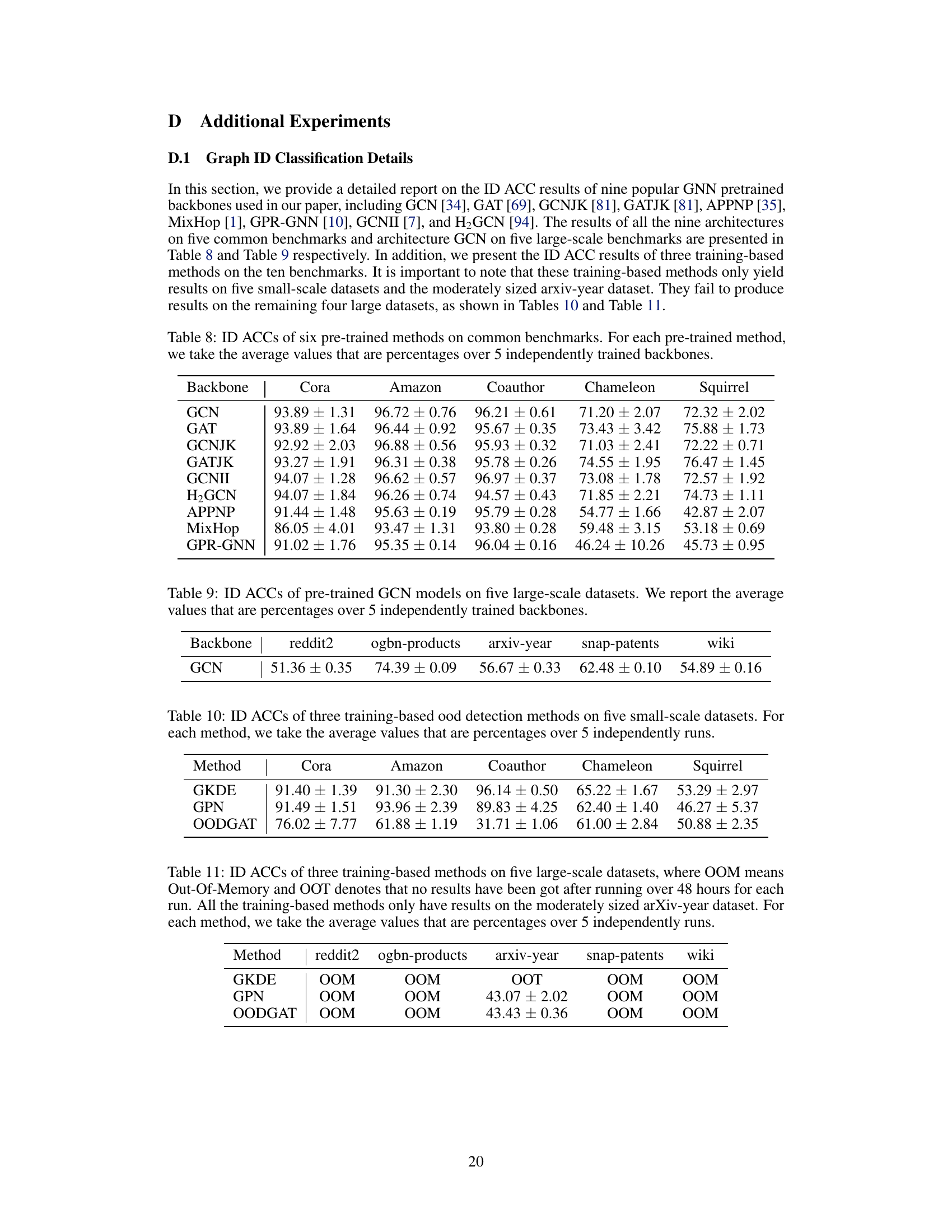
This table presents key statistics for ten real-world datasets used in the experiments. Each row represents a dataset, providing information on the number of training nodes (|Vi|), the number of in-distribution test nodes (|Vuid|), the number of out-of-distribution test nodes (|Vuood|), the number of classes (C), the overall scale of the dataset (SM for small, LG for large), and whether the dataset exhibits homophily (a tendency for nodes of the same class to be connected). This information is crucial for understanding the characteristics of the datasets and how they impact the performance of the out-of-distribution detection methods.
In-depth insights#
Score Propagation#
Score propagation, in the context of graph out-of-distribution (OOD) detection, is a post-hoc method that enhances existing OOD detection techniques by leveraging the graph’s structure. It involves propagating initial OOD scores across neighboring nodes, allowing scores to influence each other. While seemingly simple and effective, the study reveals that naive score propagation isn’t always beneficial. Its effectiveness hinges on the balance of intra-edges (connections within ID or OOD nodes) and inter-edges (connections between ID and OOD nodes). When inter-edges dominate, propagation can hurt performance. The key insight is that a favorable ratio of intra-edges to inter-edges is crucial for successful score propagation. This understanding motivates a novel edge augmentation strategy, which improves OOD detection by strategically adding edges to enhance the intra-edge ratio. This strategy is shown to improve OOD detection significantly, outperforming various baselines.
Graph Augmentation#
The concept of ‘Graph Augmentation’ in this context likely refers to methods used to enhance a graph’s structure or features to improve model performance, particularly in out-of-distribution (OOD) detection. This often involves strategically adding or removing edges, potentially based on node characteristics or predicted labels. The effectiveness of graph augmentation hinges on carefully balancing the addition of intra-edges (edges between nodes of the same class) and inter-edges (edges between nodes of different classes). An augmentation strategy that heavily favors intra-edges can boost performance by making in-distribution data more distinct from OOD data, enabling more accurate classification. Theoretical guarantees are often sought to ensure this improved performance, relying on probabilistic models of edge generation to demonstrate the conditions under which augmentation will indeed improve results. The optimal augmentation strategy usually involves identifying a subset of nodes, possibly using some prediction, and applying the changes only to that subset, rather than globally modifying the whole graph. This targeted augmentation helps to avoid the potential pitfalls of over-smoothing and confirmation bias, which can lead to reduced efficacy if augmentation is applied indiscriminately. Ultimately, graph augmentation aims to improve model robustness and accuracy for OOD detection by improving the underlying graph structure and its representation of the data.
Theoretical Insights#
A theoretical insights section in a research paper would delve into the fundamental mechanisms driving the observed phenomena. For example, in a paper about a novel graph-based anomaly detection method, this section might rigorously prove why certain graph structural properties (e.g., edge density, community structure) impact the algorithm’s performance. It would likely present formal mathematical models, theorems, or lemmas supported by detailed proofs to explain these relationships. The insights are valuable as they move beyond empirical observations, offering a deeper understanding of the underlying principles, enabling informed design choices, and ultimately bolstering the credibility of the proposed method. Clearly articulated assumptions underpinning the theoretical analysis are crucial for ensuring that the conclusions are valid and robust.
Empirical Results#
An Empirical Results section in a research paper should present a thorough and detailed analysis of experimental findings. It should clearly state the goals of the experiments and how they relate to the paper’s hypotheses. The methods used for data collection and analysis must be precisely described to ensure reproducibility. Key metrics used to evaluate performance should be clearly defined, and results should be presented using appropriate visualizations like tables and graphs. Crucially, the results must be discussed thoughtfully, highlighting significant findings, comparing performance across different methods or conditions, and explaining any unexpected results. Any limitations of the experimental design or analysis should be openly acknowledged. The section should conclude by summarizing the key findings and their implications for the broader research questions.
Future Directions#
Future research could explore more sophisticated graph augmentation strategies than simply adding edges, perhaps incorporating node features or incorporating node attributes into the augmentation process. A deeper investigation into the theoretical underpinnings of score propagation, particularly concerning its sensitivity to different graph structures and data distributions, would be valuable. Developing more robust and efficient OOD scoring functions tailored specifically for graph data is crucial. Finally, extensive empirical evaluations across a wider range of graph datasets and tasks are needed to solidify the claims and demonstrate the broader applicability of the proposed method and variations thereof. Exploring the potential benefits of combining score propagation with other OOD detection techniques is also a promising avenue.
More visual insights#
More on figures
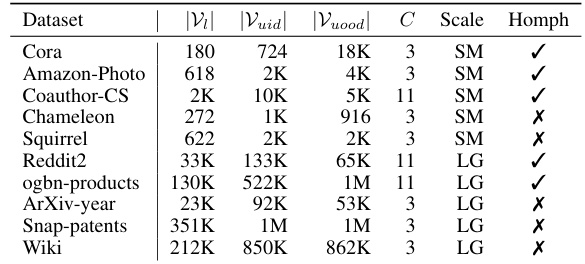
This figure illustrates two scenarios where OOD score propagation either helps or harms the performance of graph OOD detection. In (a), a graph with mostly inter-edges (connections between ID and OOD nodes) is shown, where propagation leads to misclassification. In (b), a graph with mostly intra-edges (connections between ID nodes or between OOD nodes) is shown, where propagation improves classification accuracy, demonstrating that the ratio of intra-edges to inter-edges is a critical factor influencing score propagation’s effectiveness.
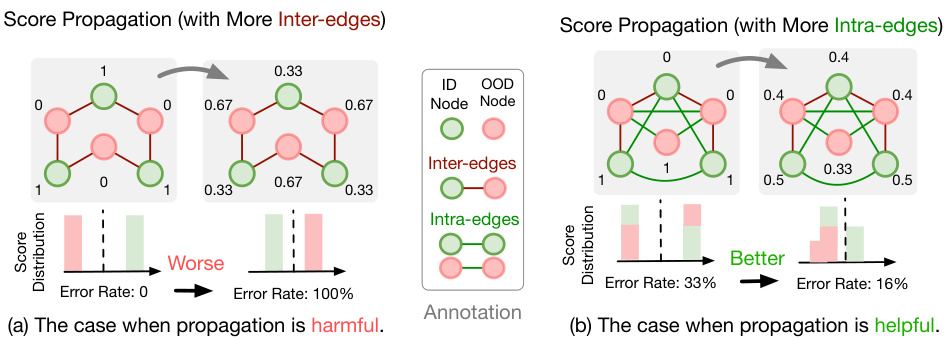
The figure illustrates the process of augmenting a graph’s adjacency matrix (A) by adding edges to a subset of nodes (G). The leftmost matrix represents the original adjacency matrix A. The grayed-out portion in the center of the rightmost matrix represents the subset of nodes (G = {v1, v2}). Edges are added between nodes within this subset, and the resulting augmented adjacency matrix (A + E) is shown on the right. This augmentation is designed to increase the ratio of intra-edges (connections within ID or OOD nodes) to inter-edges (connections between ID and OOD nodes), thereby improving the effectiveness of score propagation for OOD detection.
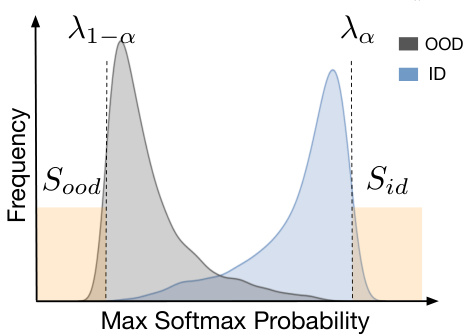
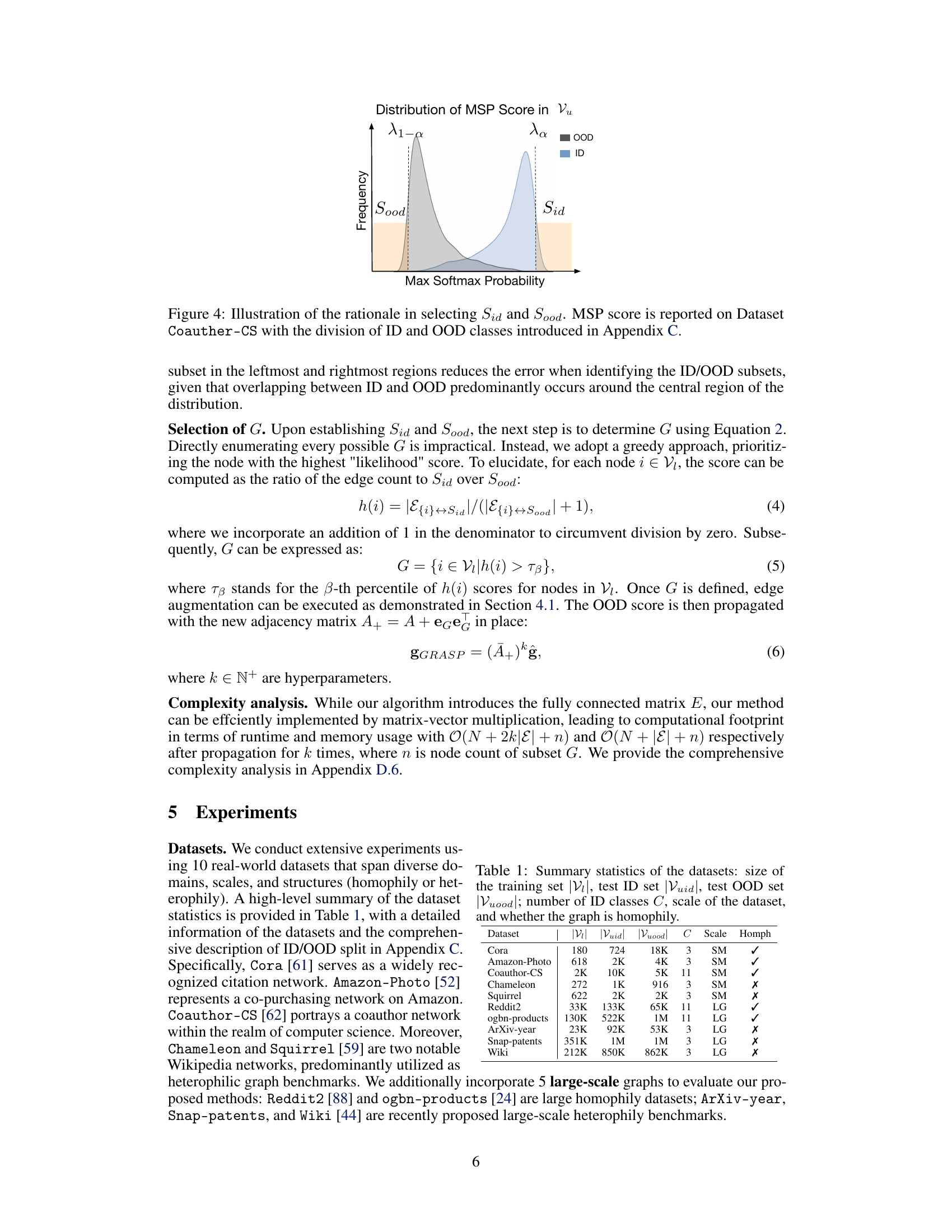
This figure illustrates how the subsets Sid and Sood are selected from the test set based on the maximum softmax probability (MSP) scores. The MSP scores are shown to follow a distribution, with the ID nodes concentrated towards higher MSP scores and OOD nodes concentrated towards lower MSP scores. Two thresholds, λa and λ1−a, are used to select the nodes with high confidence as ID (Sid) and nodes with low confidence as OOD (Sood). The rationale is that by selecting nodes in the extreme regions of the distribution, there is less overlap between ID and OOD nodes, which reduces the error rate in identifying each group.
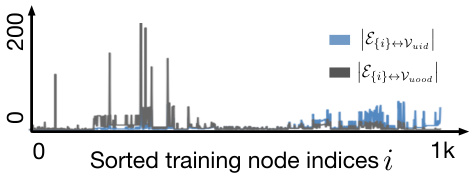
This figure shows the number of edges connecting each training node to the identified in-distribution (Sid) and out-of-distribution (Sood) nodes on the Chameleon dataset. The training nodes are sorted on the x-axis based on their h(i) score (Equation 4), which represents the ratio of edges connecting to Sid vs. Sood. The figure visually demonstrates that nodes with higher h(i) scores (right side) tend to have more connections to in-distribution nodes, supporting the proposed edge augmentation strategy.
This figure shows the rationale for selecting the subsets Sid and Sood using the MSP score. The MSP score is used to identify nodes with high and low confidence in classification, which are used to represent in-distribution (ID) and out-of-distribution (OOD) subsets respectively. The figure illustrates the distribution of MSP scores, showing subsets Sid and Sood in the marginal regions.

The figure shows a strong positive correlation between the ratio of intra-edges in a graph and the AUROC (Area Under the Receiver Operating Characteristic curve) of the out-of-distribution (OOD) detection performance. This visualization empirically supports the theoretical findings of the paper, demonstrating that increasing the proportion of intra-edges (edges connecting nodes within the same class) enhances the effectiveness of the proposed OOD detection method.
More on tables
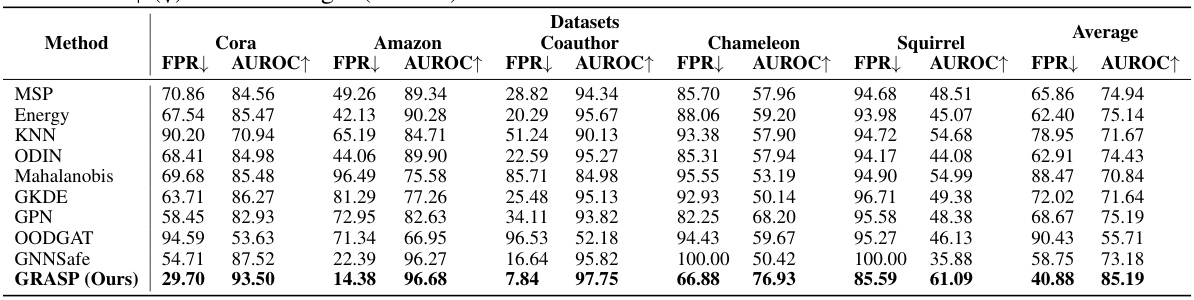
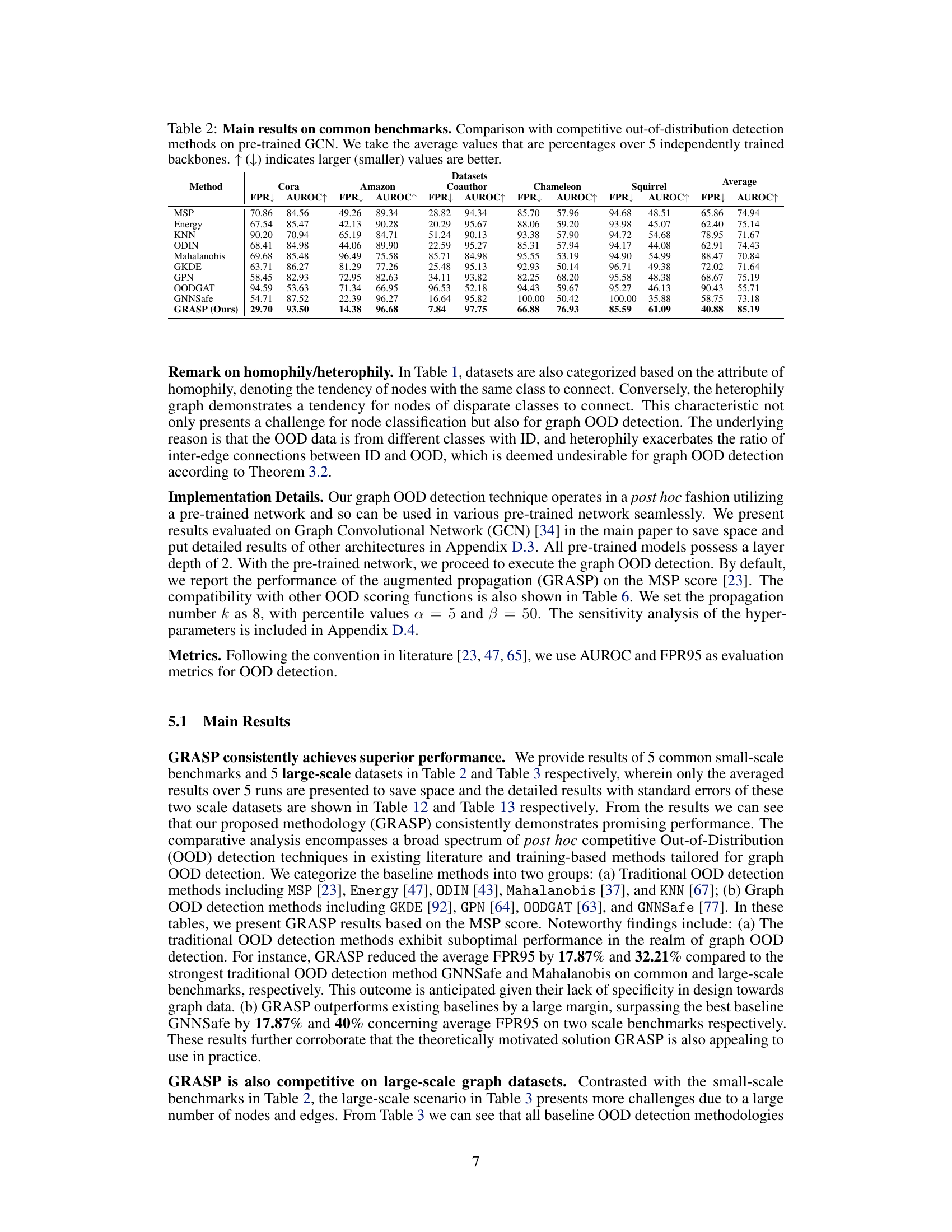
This table compares the performance of the proposed GRASP method with several other out-of-distribution detection methods on five common benchmark datasets using pre-trained Graph Convolutional Networks (GCNs). It shows the False Positive Rate (FPR) at 95% recall (FPR95) and the Area Under the Receiver Operating Characteristic curve (AUROC) for each method. Lower FPR95 and higher AUROC indicate better performance. The average performance across all datasets is also presented.
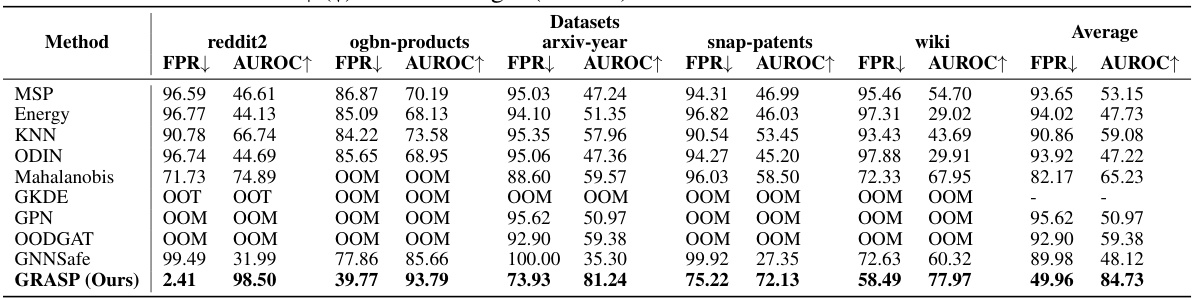
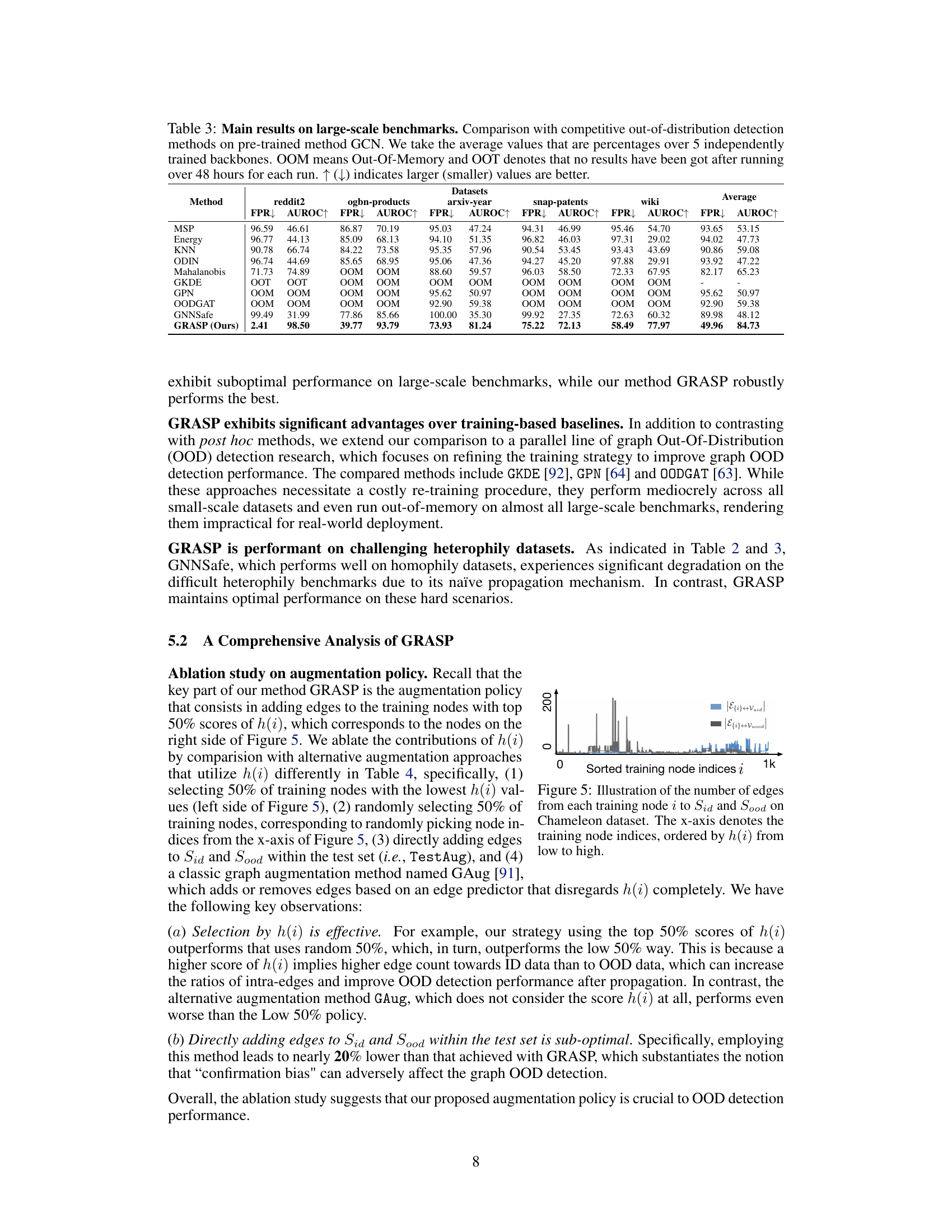
This table presents the results of the proposed GRASP method and several baseline methods for out-of-distribution (OOD) detection on five large-scale graph datasets. It compares performance using AUROC and FPR95 metrics, averaging results across five independently trained GCN models. The table also notes instances where methods ran out of memory (OOM) or did not produce results after 48 hours (OOT).
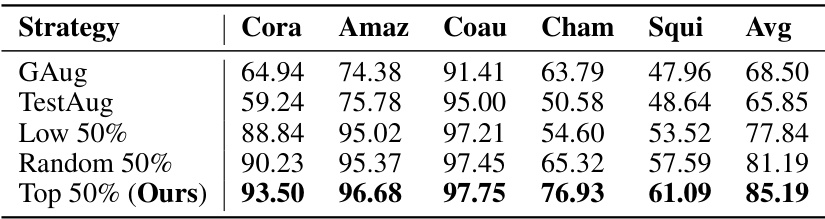
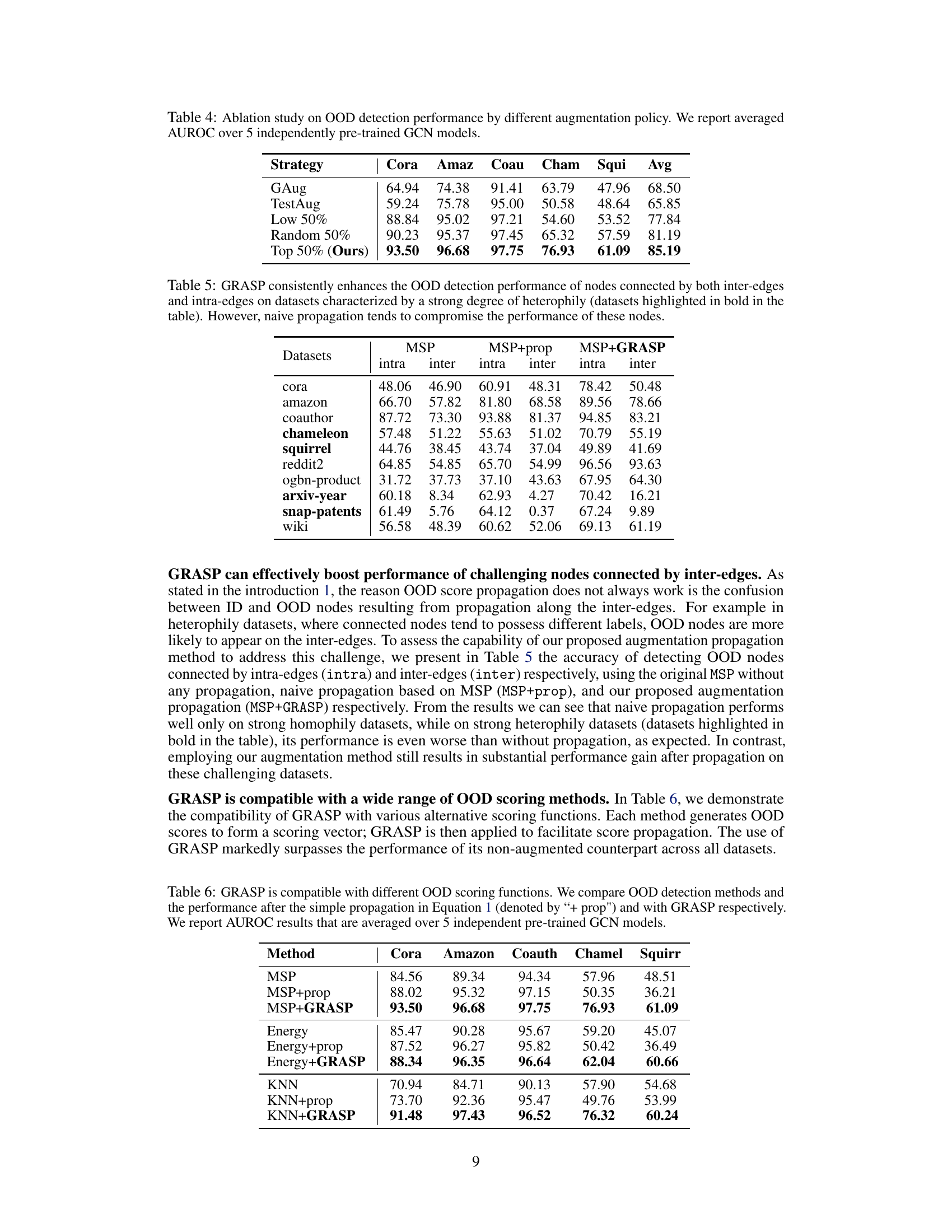
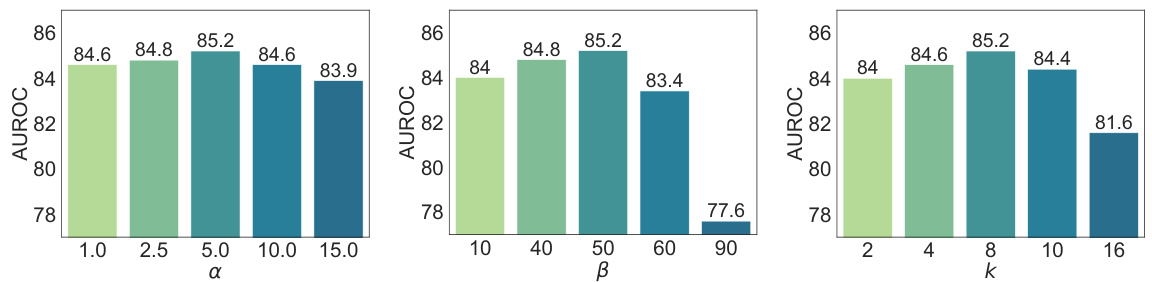
This table presents the results of an ablation study on the effect of different augmentation policies on OOD detection performance. The study compares several methods of augmenting the training data, including using a greedy approach based on the proposed h(i) score (Top 50%), randomly selecting training nodes, selecting the bottom 50% of nodes according to h(i), and using a standard graph augmentation technique (GAug). TestAug represents an alternative augmentation strategy which directly applies augmentations to the test dataset. The results show that the proposed strategy (Top 50%) significantly outperforms the other methods across multiple datasets, demonstrating its effectiveness in enhancing OOD detection.
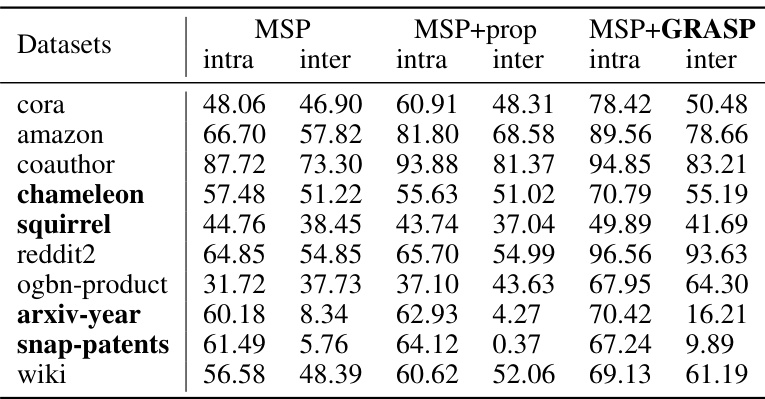
This table compares the performance of three methods for out-of-distribution (OOD) detection on nodes with different edge types (intra-edges and inter-edges). The methods are: MSP (Maximum Softmax Probability), MSP+prop (MSP with naive score propagation), and MSP+GRASP (MSP with the proposed graph augmentation and score propagation). The results show that GRASP significantly improves OOD detection, especially on heterophilic graphs where naive propagation is less effective. The datasets with strong heterophily are highlighted in bold.

This table compares the performance of different OOD scoring functions (MSP, Energy, KNN) with and without score propagation and with the proposed GRASP method. It shows that GRASP consistently improves the AUROC (Area Under the Receiver Operating Characteristic curve) across all datasets and scoring functions, demonstrating its effectiveness as a general enhancement to OOD detection.
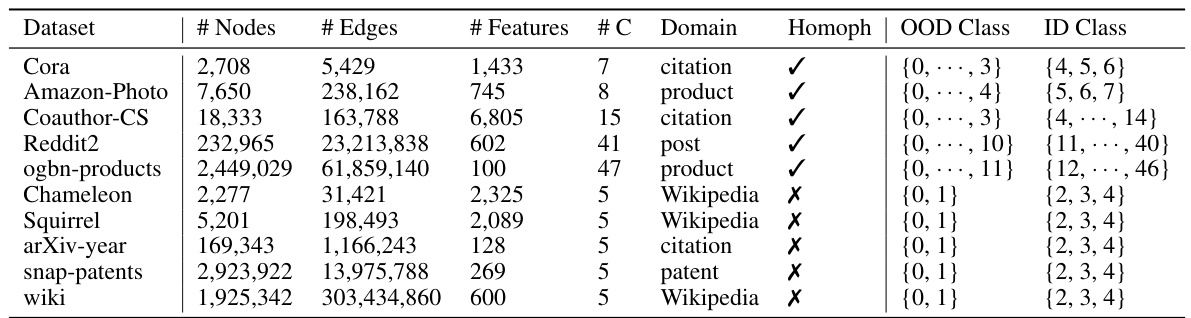
This table presents the statistics of ten real-world datasets used in the experiments. For each dataset, it shows the number of nodes, edges, features, number of classes (C), the domain the data comes from, whether the graph is homophilic or heterophilic, the range of indices representing the out-of-distribution (OOD) class, and the range of indices for the in-distribution (ID) class.

This table shows the ID accuracy (ACC) for six different pre-trained graph neural network (GNN) models across five common benchmark datasets. The average ACC is reported, calculated from five independent training runs for each model on each dataset, providing a more robust measure of performance.

This table shows the In-distribution accuracy (ID ACC) of Graph Convolutional Network (GCN) models pretrained on five large-scale datasets. The average ID ACC across five independently trained GCN backbones is reported for each dataset. The results demonstrate the performance of the pre-trained models on these large datasets before the OOD detection task is applied.

This table presents the In-distribution accuracy results of three training-based out-of-distribution detection methods on five small-scale benchmark datasets. The results are averaged over five independent runs for each method, showing the ID ACC (In-distribution accuracy) with standard error for each method on each dataset.

This table shows the ID accuracy (ACC) of three training-based out-of-distribution (OOD) detection methods on five large-scale graph datasets. The results highlight the limited applicability of training-based methods to large-scale datasets due to the high computational cost and memory requirements. Only the arXiv-year dataset produced results for all three methods. The table reports the average ACC across five independent runs for each method.

This table presents the main results of the proposed GRASP method and various baseline methods on five common graph datasets (Cora, Amazon-Photo, Coauthor-CS, Chameleon, Squirrel). It shows the performance comparison in terms of AUROC and FPR95. The results are averaged over five independently trained GCN backbones. The table highlights the consistent superior performance of GRASP across various datasets and baselines, showcasing its effectiveness as a graph OOD detection method.
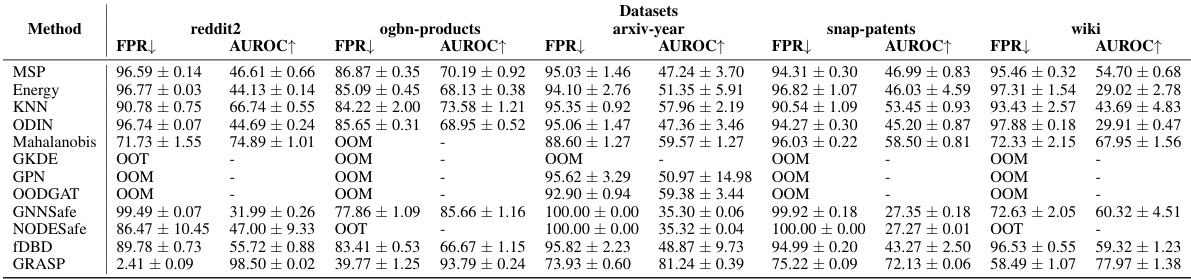
This table presents the performance comparison of the proposed method (GRASP) with other state-of-the-art methods for out-of-distribution detection on five large-scale graph datasets. The results show the average values and standard errors over five independently trained GCN backbones. ‘OOM’ indicates that the method ran out of memory, and ‘OOT’ indicates that no results were obtained after running for 48 hours.

This table presents the results of applying various pre-trained Graph Neural Network (GNN) architectures to the task of Out-of-Distribution (OOD) detection. It shows the performance of different OOD detection methods across multiple datasets using various GNN backbones, allowing for a comparison of the methods’ effectiveness across different architectures and data. The table shows False Positive Rate (FPR) and Area Under the Receiver Operating Characteristic Curve (AUROC) metrics to quantify performance.

This table presents the ratios of intra-edges (Nintra) and the area under the receiver operating characteristic curve (AUROC) scores for OOD detection before and after applying graph augmentation on several benchmark datasets. It demonstrates the impact of increasing intra-edges (by augmentation) on the OOD detection performance, showcasing the effectiveness of the proposed augmentation strategy in improving the results.
This table presents the main results of the proposed method (GRASP) and several competitive out-of-distribution (OOD) detection methods on five common benchmark datasets. The results are averaged over five independently trained graph convolutional network (GCN) backbones to ensure robustness. The table compares various metrics, including False Positive Rate (FPR) and Area Under the Receiver Operating Characteristic Curve (AUROC), to evaluate the performance of each method in detecting OOD nodes.
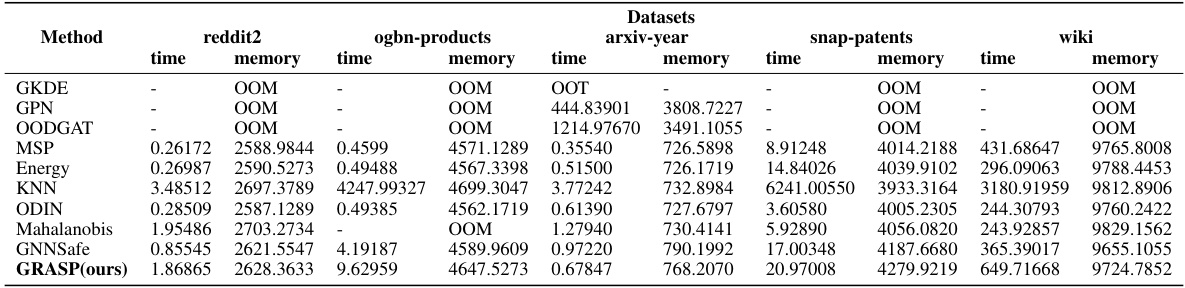
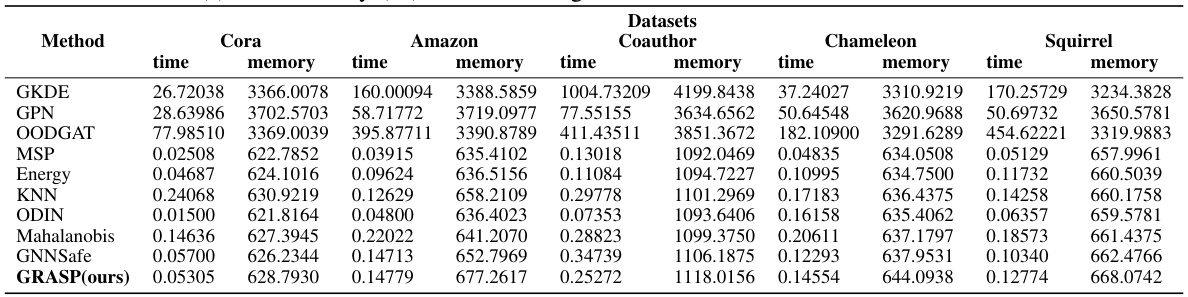
This table compares the runtime and memory usage of various algorithms (including GRASP) on five large-scale graph datasets using the GCN backbone. The results show the time in seconds and memory consumption in megabytes for each method on each dataset, illustrating efficiency differences between the methods.
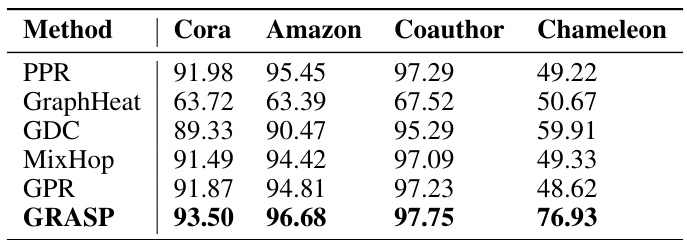
This table compares the AUROC (Area Under the Receiver Operating Characteristic curve) scores achieved by several classical propagation methods and GRASP on four different datasets. The methods compared include Personalized PageRank (PPR), Heat Kernel Diffusion (GraphHeat), Graph Diffusion Convolution (GDC), Mixing Higher-Order Propagation (MixHop), and Generalized PageRank (GPR). The table shows that GRASP consistently outperforms these other methods, achieving substantially higher AUROC scores on each dataset.

This table presents the AUROC results of several classical graph propagation methods (PPR, GraphHeat, GDC, MixHop, GPR) and the proposed GRASP method on four large-scale benchmark datasets (Squirrel, arXiv-year, snap-patents, wiki). It shows the performance variation across different propagation methods, highlighting the consistent superior performance of GRASP compared to the other methods.
Full paper#