↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world time series datasets are segmented, meaning they are divided into subsequences, each belonging to a specific class. However, these segments often have varying durations, and labels can be inconsistent due to human error or ambiguity. Existing classification methods often struggle with these variations, making accurate predictions difficult. This is especially true when dealing with the inconsistent boundary labels that are frequently encountered in real-world applications.
The paper introduces Con4m, a new framework that directly addresses these issues. Con4m uses a consistency learning approach and leverages contextual information (from both data and labels) to make more accurate predictions. It harmonizes inconsistencies in boundary labels and demonstrates superior performance across multiple datasets, showcasing its effectiveness in handling the challenges of segmented time series with multiple classes and varying durations. This makes Con4m a valuable tool for researchers working with real-world time-series data that exhibit these common characteristics.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with segmented time series data, especially those dealing with inconsistent labels and varying durations of classes. It provides a novel framework, Con4m, and significantly improves accuracy in this challenging scenario. The theoretical analysis and extensive experiments offer valuable insights for future research into improving the robustness and performance of time series classification models.
Visual Insights#
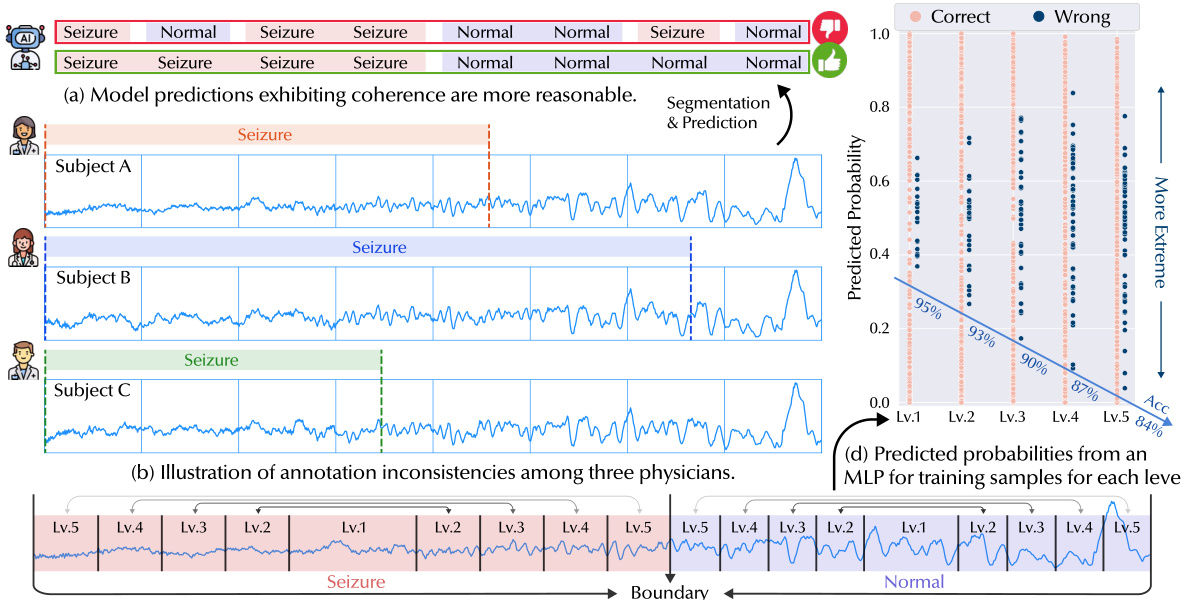
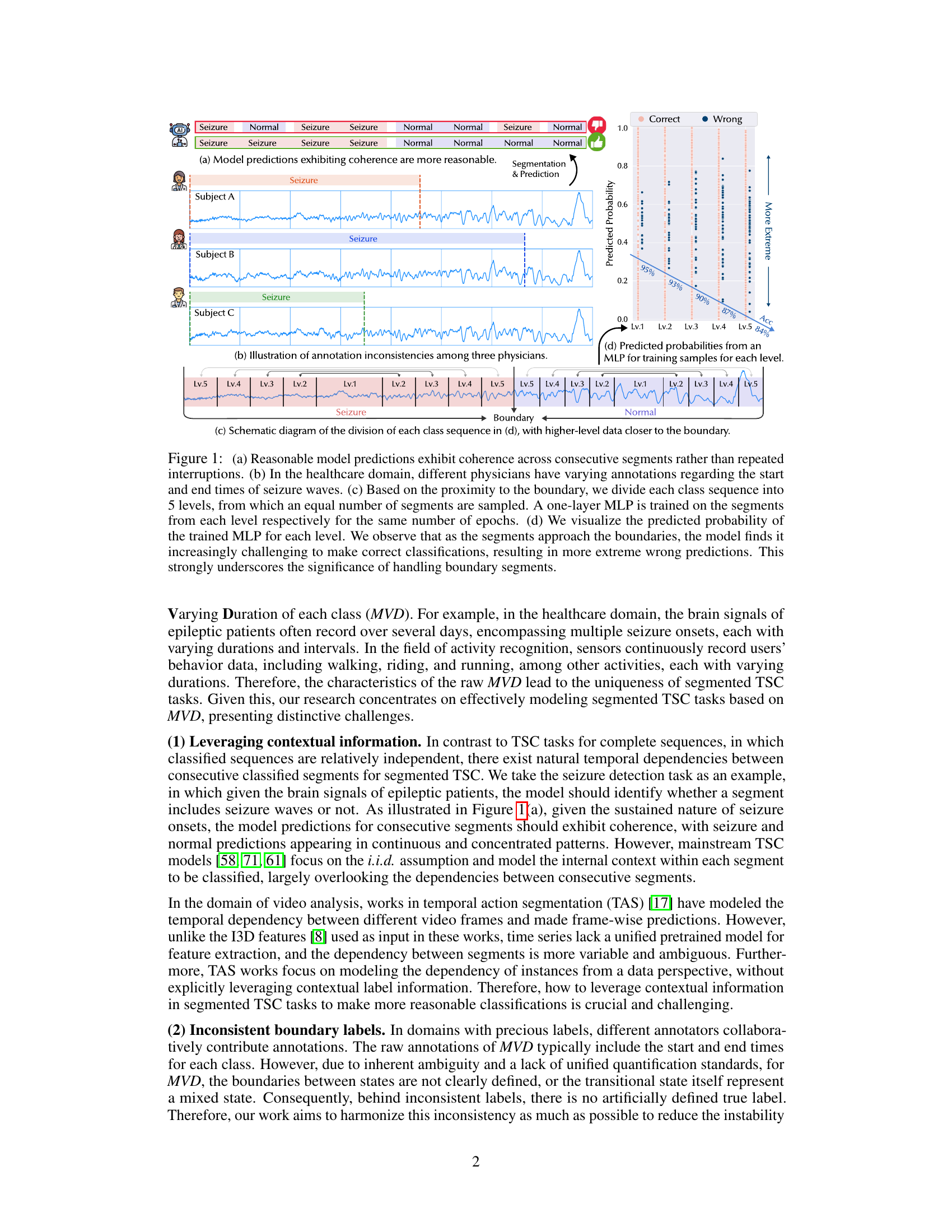
This figure shows four subfigures that illustrate the challenges of handling boundary segments in segmented time series classification tasks. Subfigure (a) shows that reasonable model predictions are coherent across consecutive segments, while subfigure (b) demonstrates the inconsistency in annotations among different physicians. Subfigure (c) describes a method for dividing class sequences into levels based on their proximity to the boundary to better understand the effect of inconsistent labels on classification performance. Finally, subfigure (d) visualizes the predicted probabilities of an MLP trained on segments from each level to show how the model’s accuracy decreases as the segments get closer to the boundaries.

This table presents a summary of the four datasets (fNIRS, HHAR, Sleep, SEEG) used in the paper’s experiments. For each dataset, it lists the sampling frequency of the data, the number of features, the number of classes, the number of subjects, the number of groups used in cross-validation, the number of cross-validation intervals, the total number of intervals, the interval length, the window length used for segmentation, the stride length, and the total number of segments. This information is crucial for understanding the experimental setup and the characteristics of the data used to evaluate the proposed Con4m model and its baselines.
In-depth insights#
Con4m Framework#
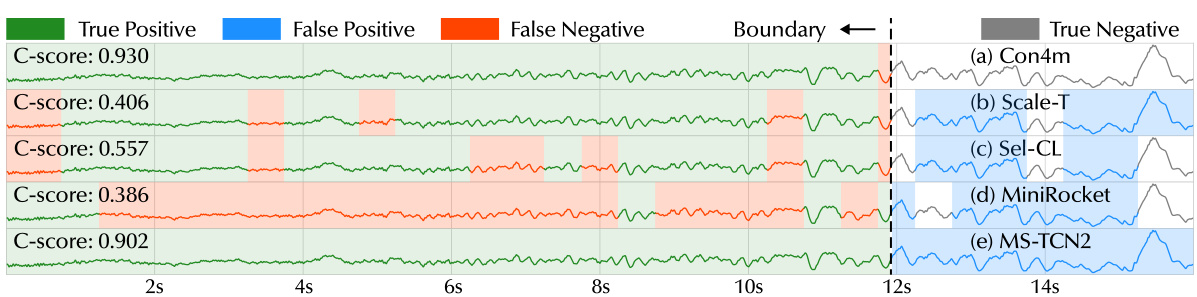
The Con4m framework tackles the challenges of segmented time series classification (TSC) with multiple classes and varying durations (MVD). It directly addresses the issue of inconsistent boundary labels, a common problem in manual annotation of MVD data, by incorporating contextual information at both data and label levels. This is achieved through a novel consistency learning approach that harmonizes inconsistent labels, improving model robustness. Con4m leverages contextual information to enhance the discriminative power of classification instances, demonstrating a formal advantage in using contextual data. The framework’s architecture uses a Con-Transformer to obtain continuous contextual representations, followed by a coherent class prediction module ensuring prediction coherence across segments. Finally, a label consistency training framework facilitates robust training by adaptively harmonizing inconsistent labels during training. The integration of these three components—contextual representation, coherent prediction, and consistent label training—makes Con4m particularly effective for MVD TSC tasks, significantly improving performance over existing methods.
Contextual Learning#
Contextual learning, in the context of segmented time series classification (TSC), focuses on leveraging the inherent relationships between consecutive segments to improve classification accuracy. Unlike traditional TSC methods that treat segments independently, contextual learning explicitly models the temporal dependencies, recognizing that adjacent segments often share related characteristics or belong to the same class. This approach is particularly beneficial when dealing with time series exhibiting a varying duration of each class (MVD) because the contextual information can help disambiguate class boundaries and handle inconsistent label annotations. By incorporating contextual priors at both the data and label levels, models can better discern patterns and make more coherent and robust predictions. Effective contextual learning strategies can involve designing architectures that incorporate neighboring segment information, such as using recurrent neural networks or attention mechanisms. Furthermore, inconsistent labeling issues can be mitigated by integrating contextual information during training, leading to more stable and reliable results, especially valuable when multiple experts annotate segments with potentially varied interpretations of class boundaries.
MVD TSC#
MVD TSC, or Multi-class Varying Duration Time Series Classification, presents a significant challenge in time series analysis due to the variability in the duration of different classes within the same time series. This characteristic, often overlooked in traditional TSC, necessitates the development of sophisticated models capable of handling temporal dependencies and inconsistencies inherent in MVD data. The core issue revolves around the difficulty in accurately segmenting the time series and assigning correct labels to segments of varying lengths, particularly near class boundaries where transitions may be ambiguous or gradual. This problem is further exacerbated by potential inconsistencies in annotations provided by different human experts. Addressing these challenges requires a deeper understanding of contextual information and the development of methods that can effectively utilize temporal context to enhance the accuracy of classification. Robust methods are essential for accurately classifying segments of varying durations, especially those at class boundaries, as well as harmonizing the often-inconsistent label annotations. The exploration of consistency learning frameworks and contextual information are key approaches to mitigate the complexities of MVD TSC.
Label Harmonization#
Label harmonization in the context of segmented time series classification with multiple classes and varying durations (MVD) addresses the challenge of inconsistent annotations. Inconsistent labeling arises from inherent ambiguities in defining class boundaries, especially in domains like healthcare, where expert opinions may differ. The core idea is to leverage contextual information, both from the data (temporal dependencies between segments) and labels (coherence in predictions), to improve model robustness. This is achieved by iteratively refining labels through a process that prioritizes easily classifiable segments (the ’easy’ part) and gradually incorporates more ambiguous segments (the ‘hard’ part). This strategy mirrors curriculum learning, making the learning process more stable. By incorporating contextual priors in a consistency learning framework, the model learns to harmonize these initially inconsistent labels, resulting in a more robust and accurate classification model. This framework tackles two critical aspects of MVD datasets: the inherent temporal dependencies between segments and the inconsistency of human-annotated labels. Thus, label harmonization in this setting isn’t just about noise reduction; it’s about effectively using contextual knowledge to refine the learning process for better generalization on MVD time series data.
Future Work#
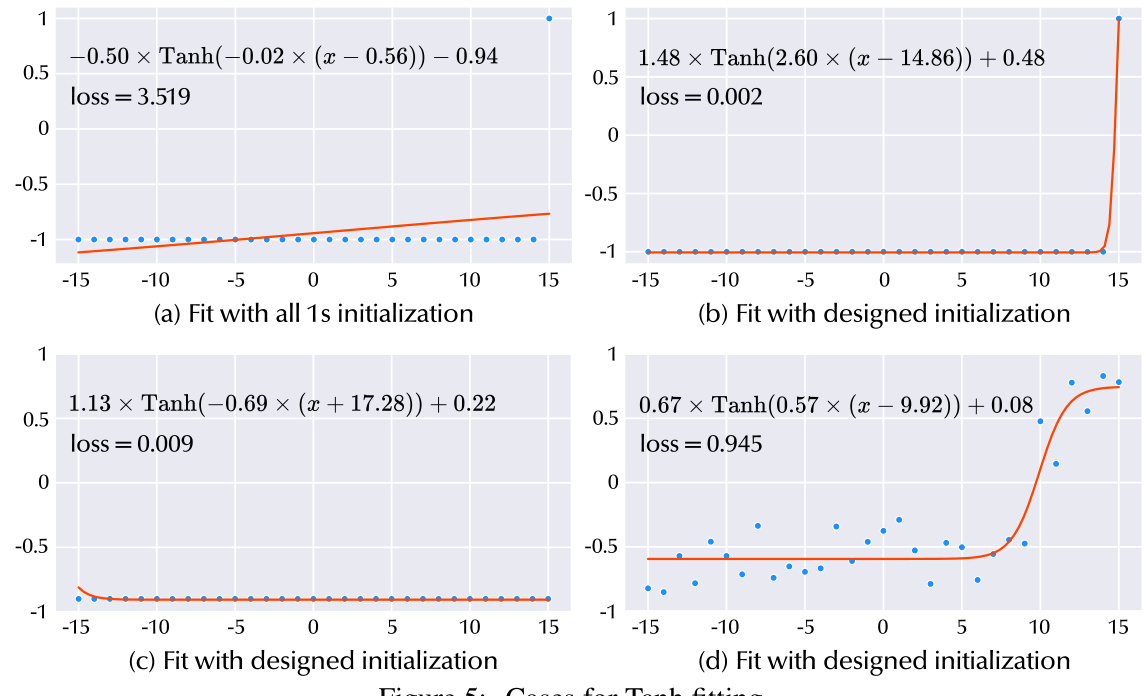
Future research directions stemming from this work could explore several promising avenues. Extending Con4m’s capabilities to handle even more complex scenarios, such as those involving high-dimensional data or imbalanced class distributions, would be beneficial. Investigating the impact of different contextual window sizes and kernel functions on performance is also warranted. The current framework primarily focuses on the temporal aspect of contextual information; exploring ways to integrate spatial or other multi-modal contextual cues could significantly broaden its applicability. Furthermore, a detailed comparative analysis against a wider range of state-of-the-art models for segmented time series classification, encompassing different architectural paradigms and learning strategies, would strengthen the evaluation and highlight Con4m’s unique contributions. Finally, exploring applications in diverse real-world domains beyond the ones studied here, such as healthcare diagnostics, finance, or environmental monitoring, could showcase its practical impact and reveal new challenges that require further refinement of the methodology.
More visual insights#
More on figures
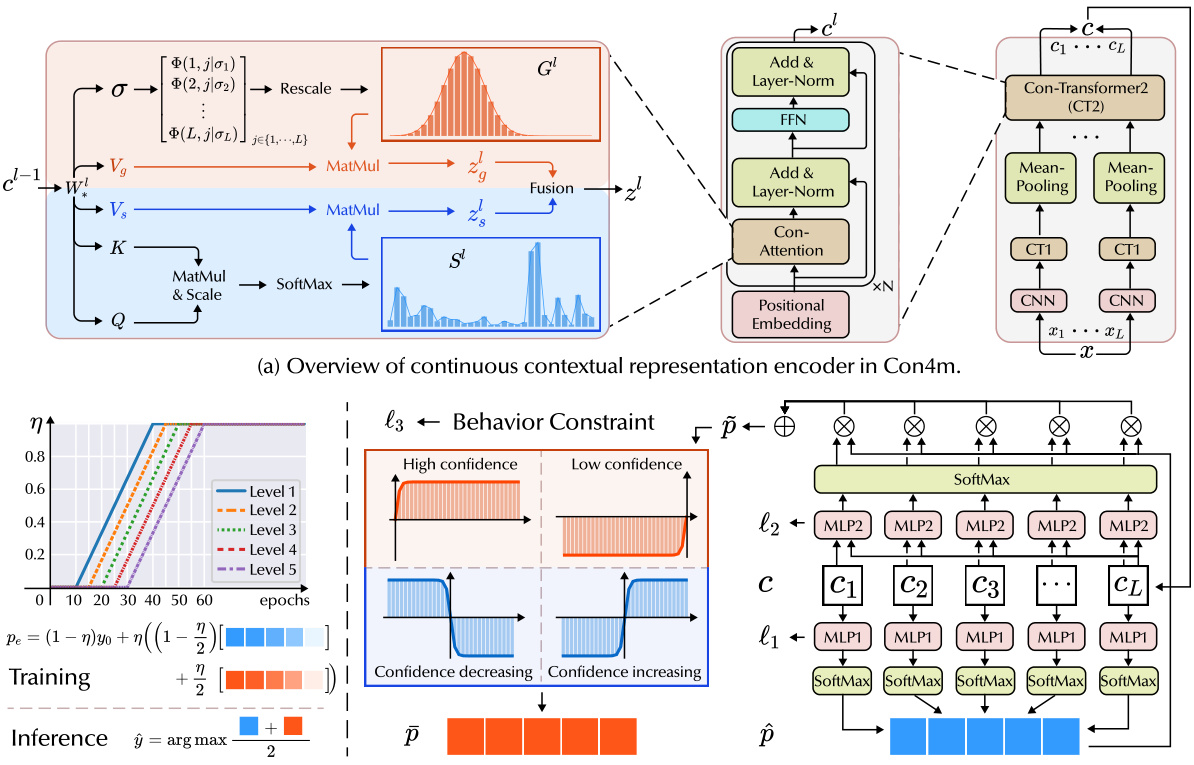
This figure provides a detailed overview of the Con4m architecture. Panel (a) illustrates the continuous contextual representation encoder, highlighting the Con-Attention mechanism and the Con-Transformer structure, which leverage contextual information to improve the discriminative power of the model. Panel (b) shows the context-aware coherent class prediction and consistent label training framework, focusing on neighbor class consistency discrimination, prediction behavior constraints, and label harmonization techniques. This framework harmonizes inconsistent labels, ensuring robustness and reliability in handling segmented time series classification tasks with varying durations.

This figure illustrates the challenges of segmented time series classification (TSC) with multiple classes and varying durations (MVD). Subfigure (a) shows ideal coherent predictions across segments. Subfigure (b) shows annotation inconsistencies among physicians in the healthcare domain (seizure detection). Subfigures (c) and (d) demonstrate that model performance deteriorates as segments approach class boundaries, highlighting the importance of handling boundary segments.
This figure shows the impact of inconsistent boundary labels on model performance in a segmented time series classification task. Subfigure (a) shows that reasonable model predictions exhibit coherence across consecutive segments, (b) illustrates inconsistencies in boundary annotations from different physicians, (c) shows how class sequences are divided into 5 levels based on their proximity to boundaries, and (d) shows the predicted probabilities from an MLP trained on segments from each level. The results highlight the challenges posed by inconsistent boundaries.
This figure demonstrates the challenges of segmented time series classification with inconsistent boundary labels. Subfigure (a) shows ideal coherent predictions across segments, contrasting with the inconsistent annotations of different physicians in (b). Subfigure (c) illustrates the methodology of dividing class sequences into levels based on proximity to boundaries, training an MLP on each level’s segments, and visualizing the resulting prediction probabilities in (d). The results in (d) highlight the decreased accuracy and increased errors near the boundaries, emphasizing the importance of handling these boundary segments.
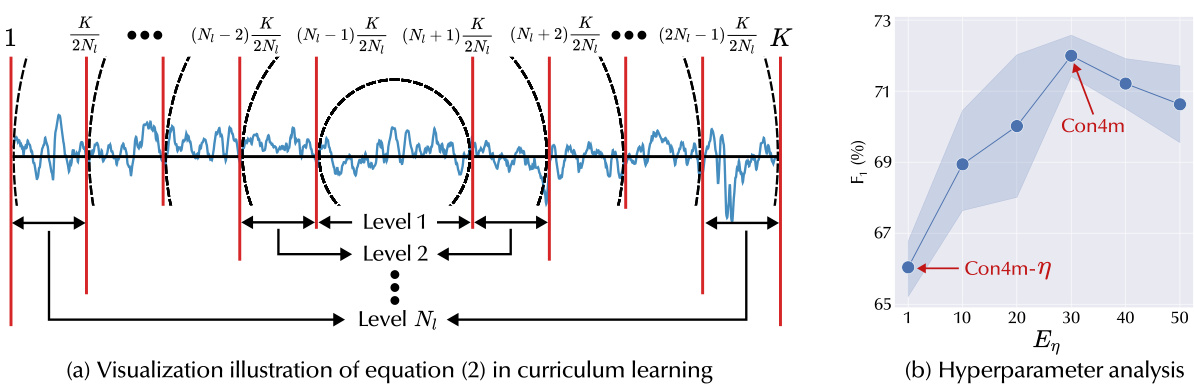
This figure demonstrates the impact of inconsistent boundary labeling on model performance in segmented time series classification (TSC). Panel (a) shows ideal coherent predictions across segments. Panel (b) illustrates inconsistencies in annotations from different physicians on seizure data. Panel (c) shows how the class sequences were divided into five levels based on proximity to the boundary, with segments sampled from each level used to train a simple MLP. Panel (d) shows that as the level (proximity to the boundary) increases, model accuracy decreases, highlighting the challenge of handling inconsistent boundary labels and the importance of contextual information.
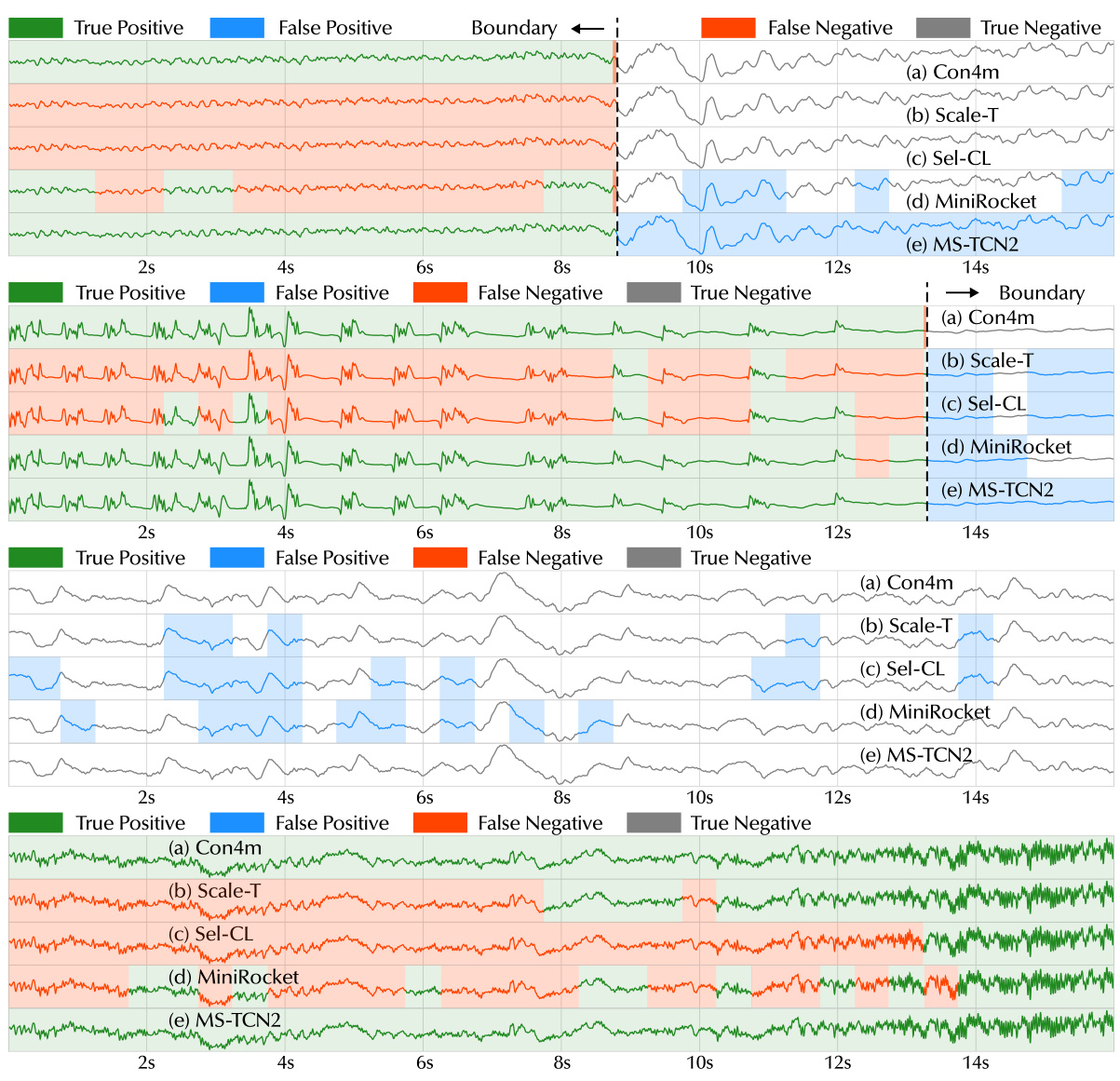
This figure demonstrates the challenges in handling boundary segments in segmented time series classification with multiple classes and varying durations (MVD). It shows that (a) coherent model predictions are expected across consecutive segments, (b) annotation inconsistencies exist among physicians in the healthcare domain, (c) dividing each class sequence into levels based on proximity to the boundary helps analyze model performance, and (d) model accuracy decreases near boundaries, highlighting the importance of handling boundary segments.
More on tables
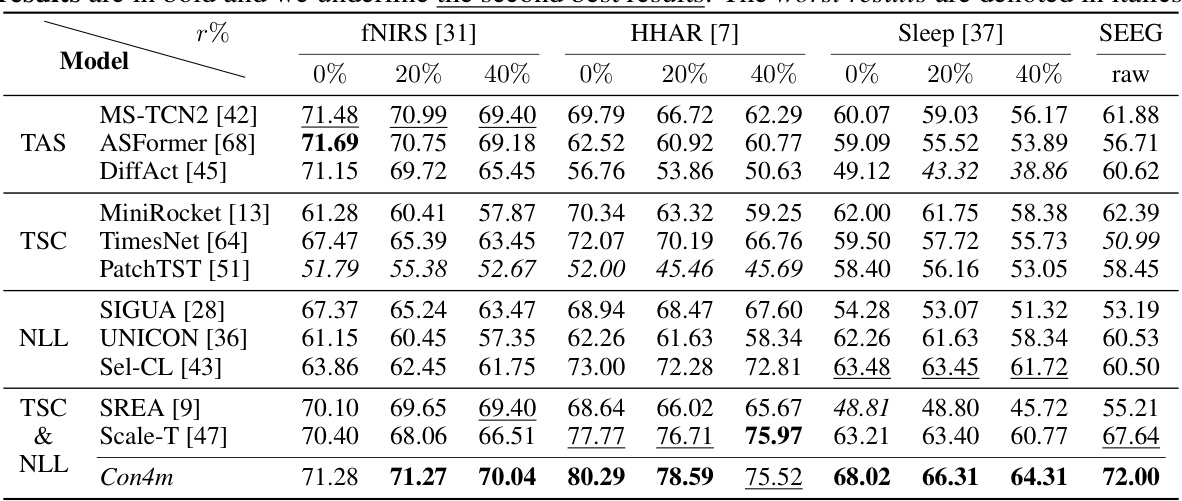
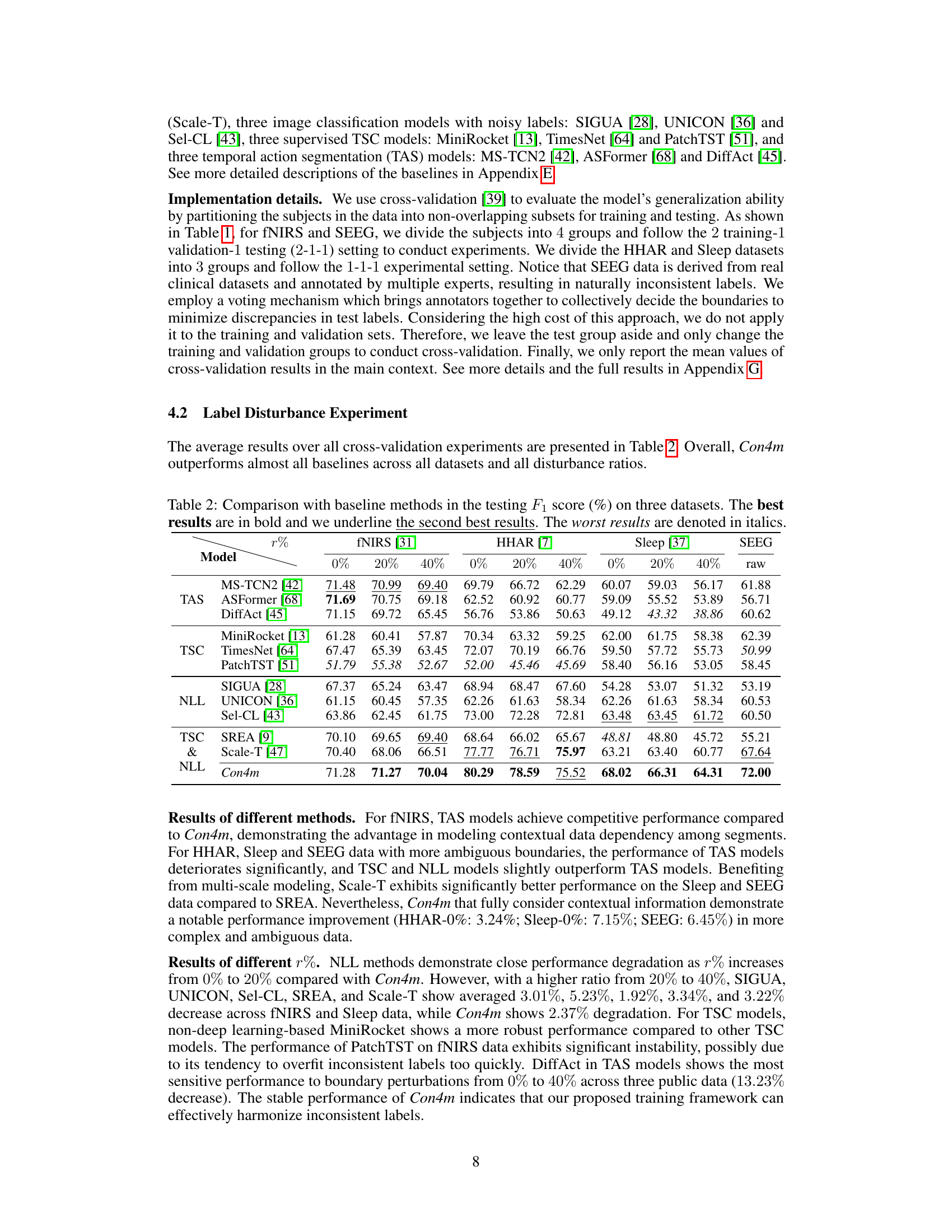
This table compares the performance of the proposed Con4m model against several baseline models across three public datasets (fNIRS, HHAR, Sleep) and one private dataset (SEEG) with varying degrees of label noise (0%, 20%, 40%). The F1-score, a common metric for evaluating classification performance, is used to assess the models’ accuracy. The best performing model for each dataset and noise level is highlighted in bold, the second-best is underlined, and the worst is italicized.

This table compares the performance of the proposed Con4m model against several baseline methods across three public datasets (fNIRS, HHAR, Sleep) at different levels of label noise (0%, 20%, 40%). The F1 score, a common metric for evaluating classification performance, is used to assess each model’s accuracy. The best performing model for each dataset and noise level is highlighted in bold, while the second-best is underlined. The worst performing model is indicated in italics. This allows for a clear comparison of Con4m’s performance against existing state-of-the-art models in the field of segmented time series classification.
This table compares the performance of the proposed Con4m model against various baseline methods across three public datasets (fNIRS, HHAR, Sleep) and one private dataset (SEEG). The comparison is made using the F1 score, a metric that balances precision and recall. The table shows the F1 scores for each method across different levels of label noise (0%, 20%, 40%) to assess the robustness of each method in handling noisy labels. The best performing method for each setting is highlighted in bold, while the second-best performing methods are underlined. The worst-performing method is shown in italics.
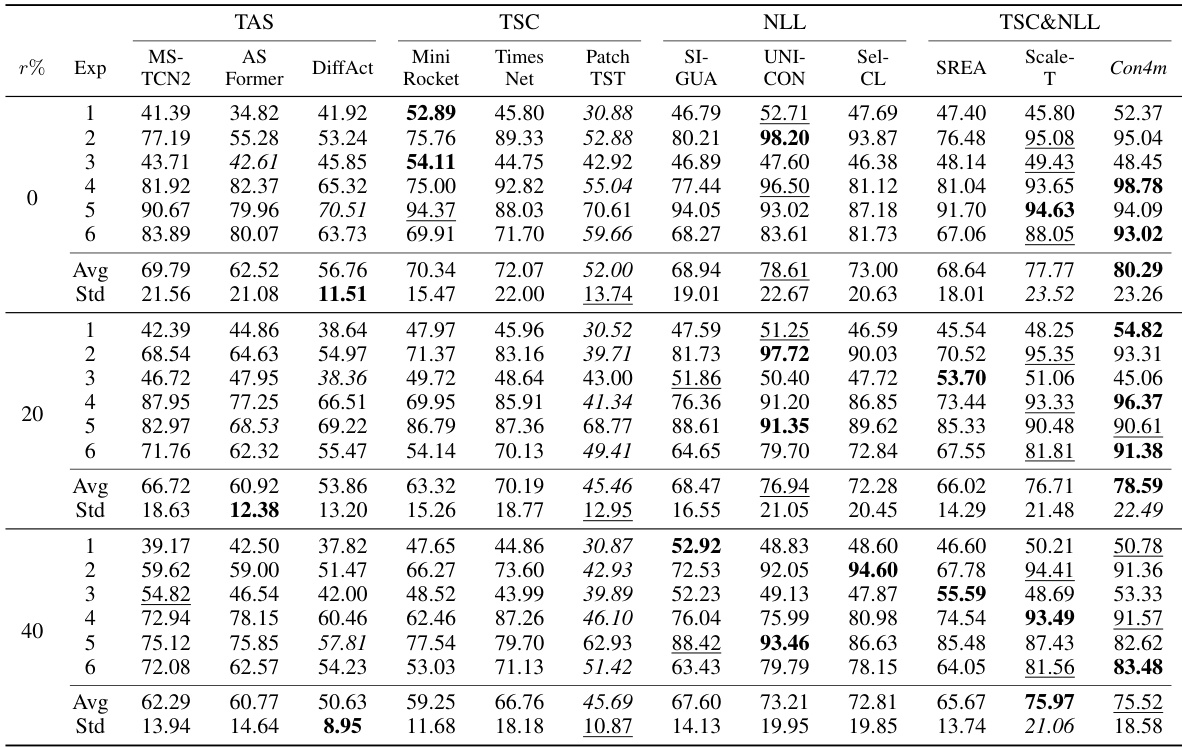
This table compares the performance of the proposed Con4m model against various baseline models (including other TSC and noisy label learning models) on three public datasets (fNIRS, HHAR, Sleep) and one private dataset (SEEG). The performance is measured using the F1 score, a common metric for evaluating classification models. The table shows the results for different noise levels (0%, 20%, 40%), and a ‘raw’ column indicates performance on the original, undisturbed data. The best and second-best results for each dataset and noise level are highlighted.
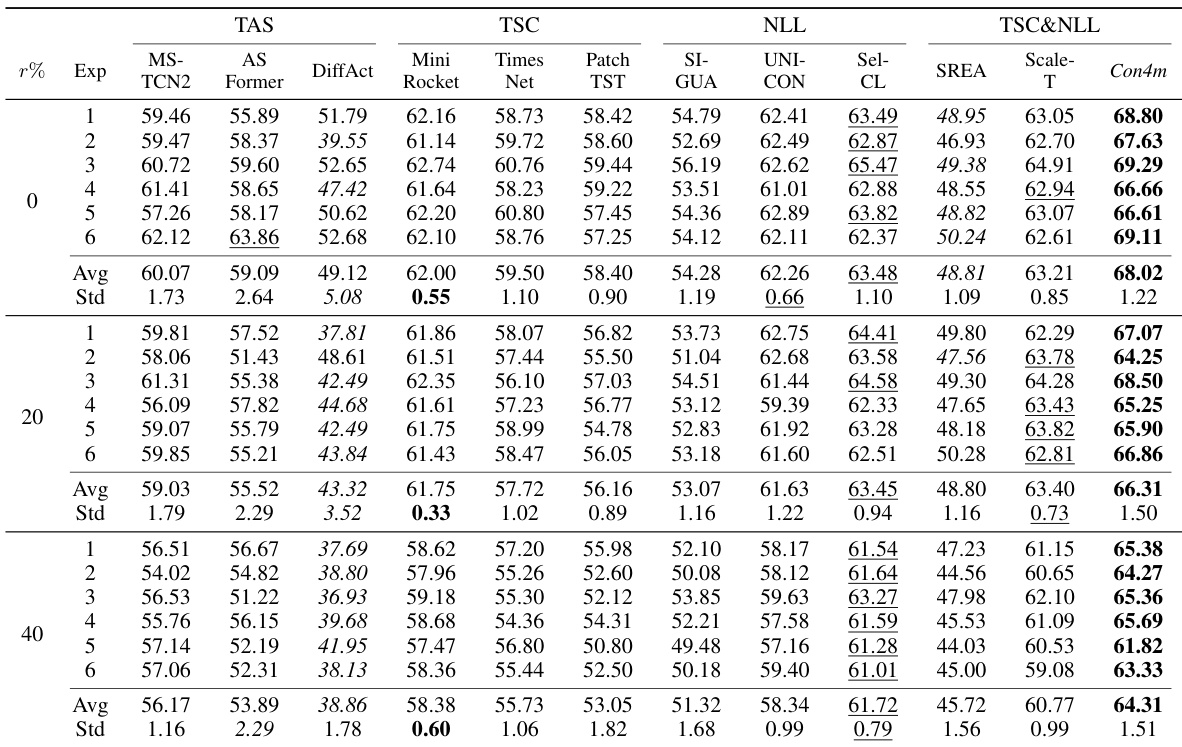
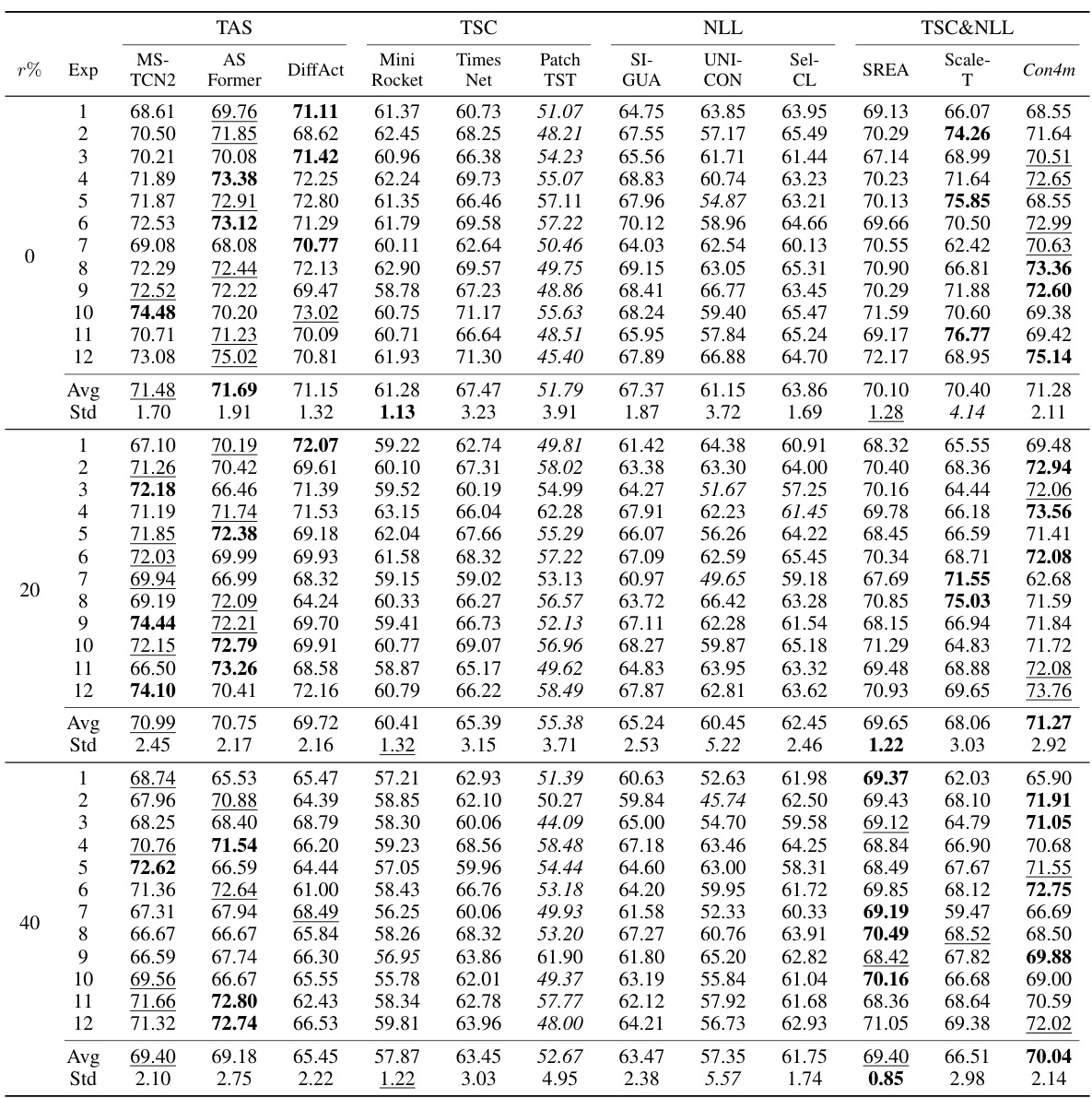
This table compares the performance of the proposed Con4m model against various baseline methods across three datasets (fNIRS, HHAR, and Sleep). The F1 score, a common metric for evaluating classification performance, is reported for each method under different conditions (0%, 20%, and 40% label disturbance). The best performing method for each dataset and condition is highlighted in bold, the second best is underlined, and the worst performing is italicized. This allows for a direct comparison of Con4m’s performance relative to existing state-of-the-art methods.
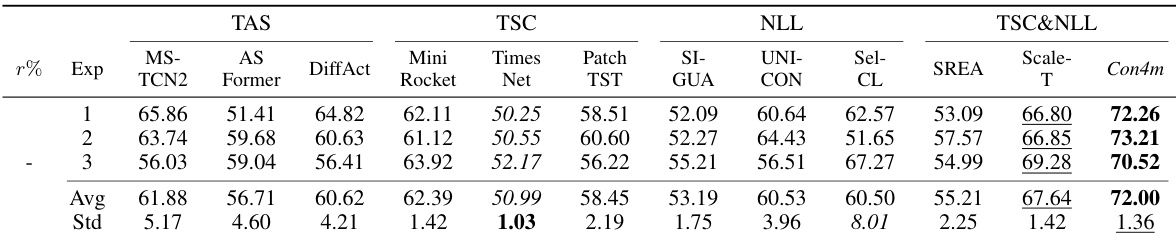
This table compares the performance of the proposed Con4m model against various baseline methods across three datasets (fNIRS, HHAR, Sleep) at different levels of label noise (0%, 20%, 40%). The F1 score, a common metric for evaluating classification performance, is used to assess each model’s accuracy. The best performing model for each dataset and noise level is highlighted in bold, the second-best is underlined, and the worst is italicized. This allows for a direct comparison of Con4m’s performance relative to state-of-the-art models in handling inconsistent labels and varying data conditions.
Full paper#