Large language model validity via enhanced conformal prediction methods

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on large language model (LLM) safety and reliability. It offers practical solutions to address the issue of LLM hallucinations and unreliable outputs, which is a major bottleneck to wider LLM adoption. The proposed methods are readily applicable to various LLM tasks, opening new avenues for research into trustworthy AI systems.

Visual Insights

#

This figure compares three outputs from a large language model (LLM) in response to a question about shingles vaccines. The first is the unfiltered LLM output. The second is filtered using the existing method by Mohri and Hashimoto, which retains only the claims exceeding a fixed 90% confidence threshold. The third output uses the authors’ new method, achieving a 63% adaptive confidence threshold while retaining approximately 70% of the original claims. This illustrates the trade-off between retaining useful information and maintaining a high probability of factual correctness.

In-depth insights

#

Conformal LLM Validity

#

Conformal prediction offers a powerful framework for enhancing the validity of Large Language Models (LLMs) by providing rigorous probabilistic guarantees on their outputs. The core idea is to calibrate an LLM’s responses using a scoring function that quantifies the confidence of each generated claim. This approach moves beyond simply assessing overall LLM accuracy and instead focuses on the factual correctness of individual claims within a response. By employing techniques like split conformal prediction, it’s possible to identify and filter out claims that fall below a certain calibrated confidence threshold. However, existing conformal methods often suffer from limitations such as a lack of conditional validity (guarantees might vary depending on the topic) and overly conservative filtering that removes too many accurate claims. To overcome these challenges, the paper introduces enhanced methods such as level-adaptive conformal prediction and conditional boosting. Level-adaptive approaches offer nuanced guarantees by adjusting the required confidence level depending on the characteristics of the prompt and response, thereby preserving more factual information. Simultaneously, conditional boosting systematically improves the quality of the scoring function through a novel algorithm that enables differentiation through the conformal procedure. These improvements contribute to obtaining highly reliable, yet practically useful, factual claims from LLMs. The method’s efficacy is demonstrated in experiments involving biography and medical question-answering datasets, highlighting improved conditional validity and more robust claim retention compared to existing techniques.

Conditional Boosting

#

The proposed technique of ‘Conditional Boosting’ ingeniously addresses the limitations of existing conformal prediction methods in the context of Large Language Models (LLMs). It tackles the challenge of improving the quality of the scoring function used to filter LLM outputs, directly impacting the balance between factual accuracy and the preservation of useful information. By introducing a novel algorithm to differentiate through the conditional conformal procedure, the method efficiently learns a superior scoring function capable of distinguishing between accurate and inaccurate claims. This addresses the problem of overly conservative filtering that previously removed valuable and correct LLM statements. Crucially, this method’s optimization directly focuses on claim retention, enhancing the practicality and usefulness of the resulting filtered LLM output. The combination of conditional conformal prediction and automated score improvement is a significant contribution to improving LLM reliability and trustworthiness.

Adaptive Conformal

#

Adaptive conformal methods represent a significant advancement in conformal prediction, offering enhanced flexibility and robustness. Unlike traditional conformal methods that use a fixed significance level, adaptive approaches dynamically adjust this level based on the characteristics of the input data. This adaptability is crucial when dealing with complex datasets exhibiting variability in uncertainty. The key benefit is improved conditional validity, ensuring that the confidence level is reliable across different subgroups of data. This also allows for greater utility, potentially avoiding overly conservative prediction sets that sacrifice valuable information for the sake of strict guarantees. The development of algorithms for differentiating through the conformal prediction process is a significant enabling factor, facilitating the design of more effective scoring functions, which are fundamental to adaptive conformal methods. Adaptive conformal methods enhance both the accuracy and usefulness of conformal predictions, especially in challenging real-world applications like large language model validation where uncertainty quantification and reliability are paramount.

Empirical Gains

#

An empirical gains analysis in a research paper would explore the practical improvements achieved by the proposed methods. It would likely involve comparisons against existing state-of-the-art techniques using relevant metrics on benchmark datasets. Quantitative results, such as increased accuracy, efficiency gains (e.g., faster processing times), or improvements in specific aspects (e.g., reduced hallucination rates in language models) would be central to this section. Qualitative observations regarding the usability, generalizability, and robustness of the methods would also be included. For example, the study might discuss whether improvements generalize across various datasets or problem domains, or it might analyze the stability and sensitivity of the methods to different parameters. Visualization techniques, such as graphs and charts, would typically support the presentation of empirical findings, highlighting the magnitude and statistical significance of the improvements. Overall, a strong empirical gains analysis demonstrates the real-world value and practical applicability of the research contributions.

Method Limits

#

A thoughtful analysis of limitations inherent in the methodology of a research paper focusing on large language model (LLM) validity would explore several key aspects. Firstly, any assumptions made about the data distribution, such as independence or exchangeability of samples, should be critically examined. Real-world data often violates such assumptions. Secondly, the choice of scoring function to assess LLM output factuality is crucial; the effectiveness of the method is directly tied to the scoring function’s accuracy, and imperfect scores could lead to erroneous filtering. Thirdly, the reliance on a calibration set introduces a potential bias and the size of this set impacts the accuracy of the method; smaller sets may lead to less reliable calibrations. Fourthly, the computational cost of the proposed methods should be addressed, especially in relation to their scalability for large LLMs and datasets. Finally, the generalizability of the methodology across diverse LLM architectures and downstream tasks is a critical concern. An in-depth analysis might also investigate the impact of data biases present in the training data used to calibrate the models on the effectiveness of the proposed validation techniques.

More visual insights

#

More on figures

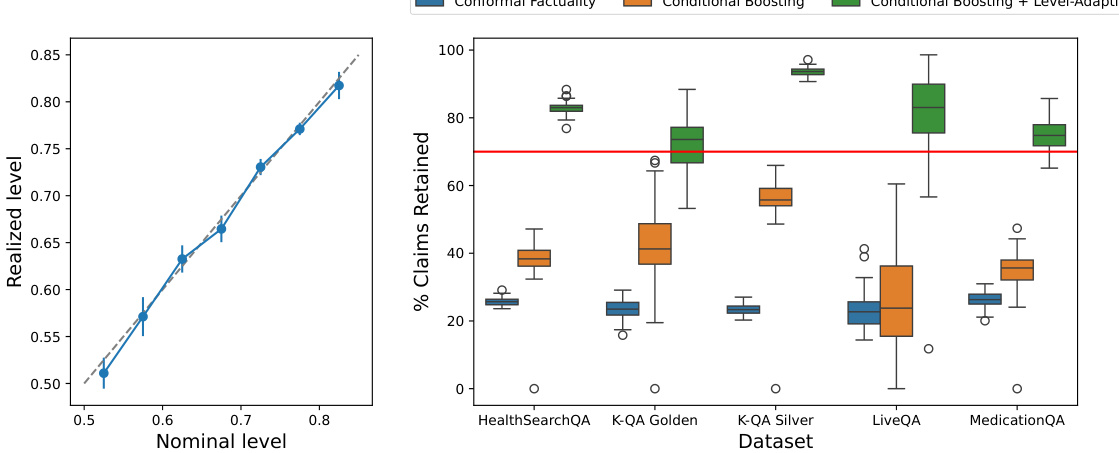
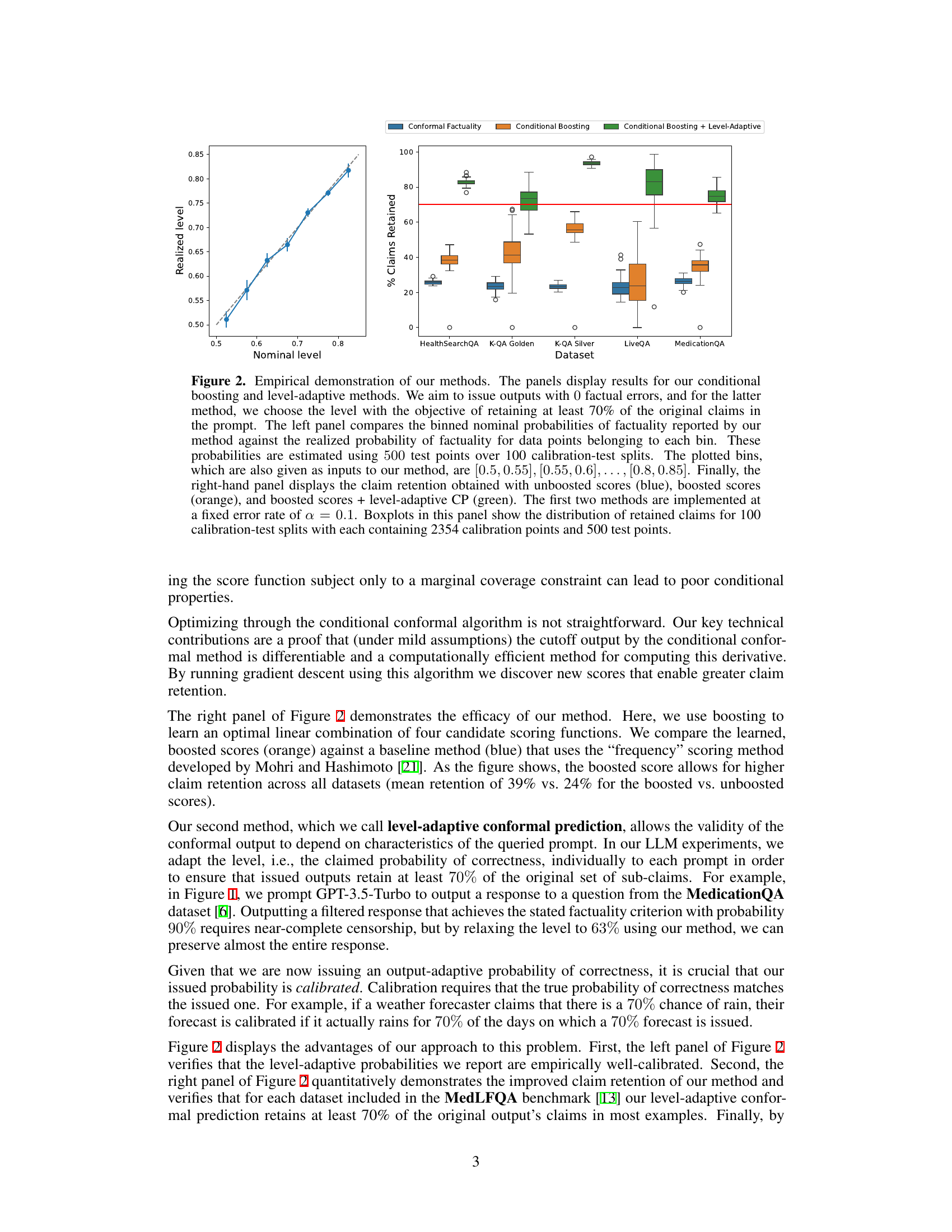
This figure empirically demonstrates the performance of the proposed conditional boosting and level-adaptive methods. The left panel shows the calibration of the methods by comparing the binned nominal probabilities of factuality against the realized probabilities. The right panel compares the claim retention achieved by different methods, showing that conditional boosting and level-adaptive approaches improve claim retention.

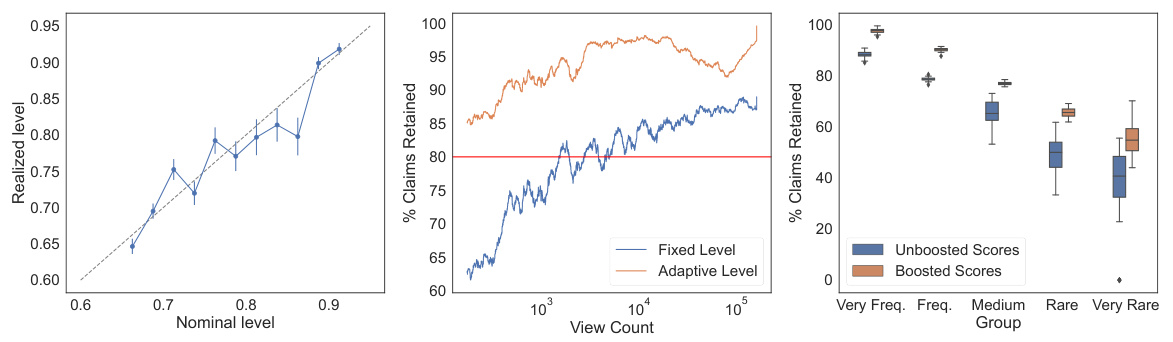
This figure empirically demonstrates the performance of the proposed conditional boosting and level-adaptive methods. The left panel shows calibration results, comparing predicted and actual factuality probabilities across different confidence levels. The right panel shows claim retention rates comparing the three proposed methods, illustrating the benefits of boosting and adaptive level selection.

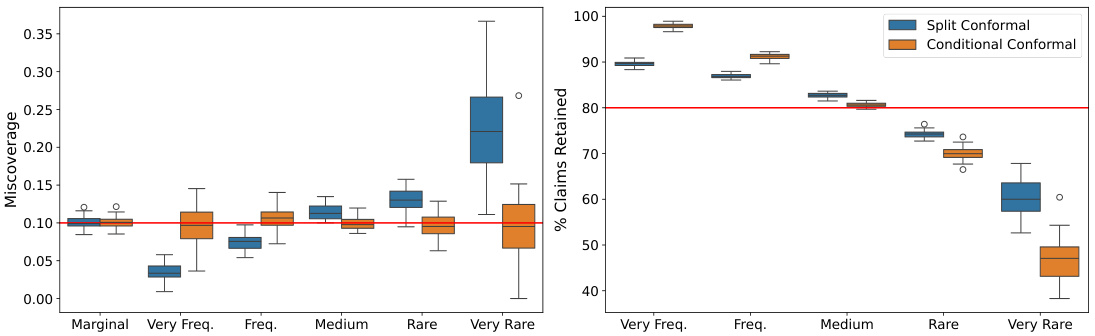
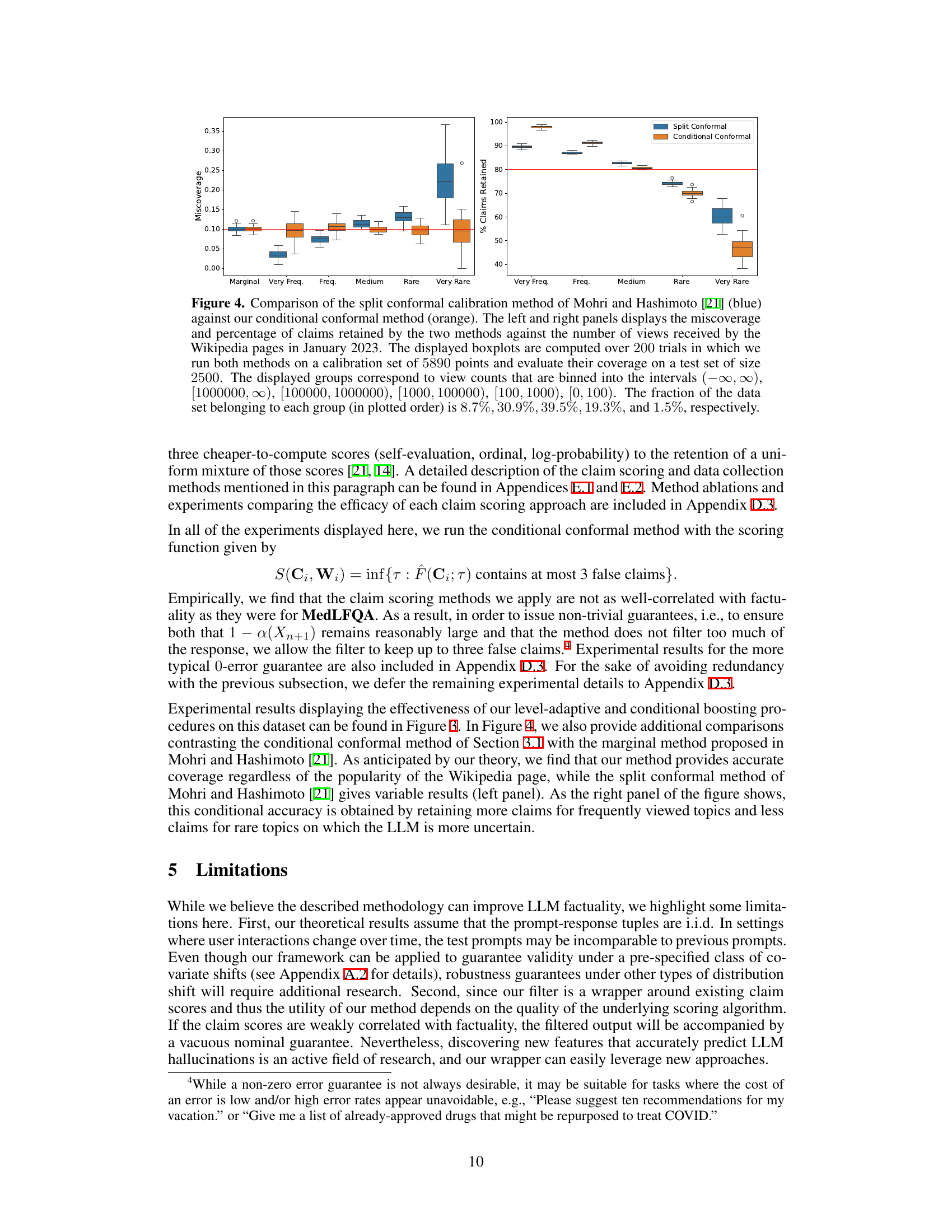
This figure compares the performance of the split conformal method from Mohri and Hashimoto [21] and the proposed conditional conformal method. The left panel shows miscoverage (the difference between the nominal and actual coverage probabilities) for different frequency groups of Wikipedia articles (based on the number of views). The right panel displays the percentage of claims retained by each method. The results are based on 200 trials with a calibration set of 5890 points and a test set of 2500 points. The Wikipedia articles are grouped by their view counts into six categories, and each category’s size relative to the total is indicated.

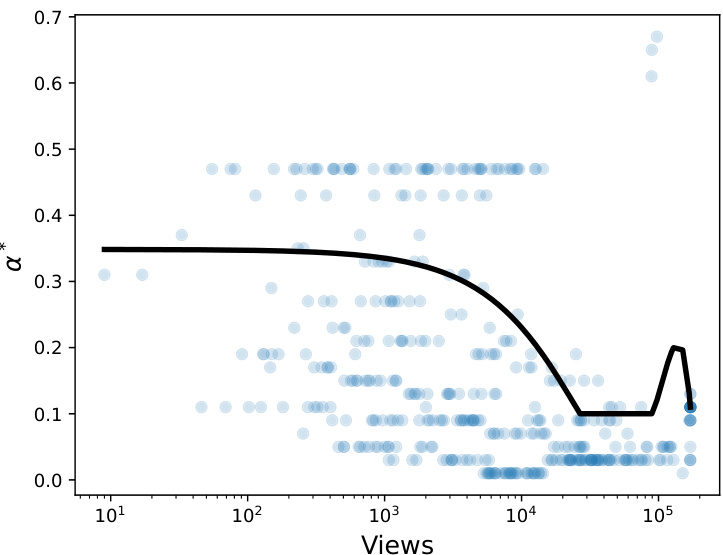
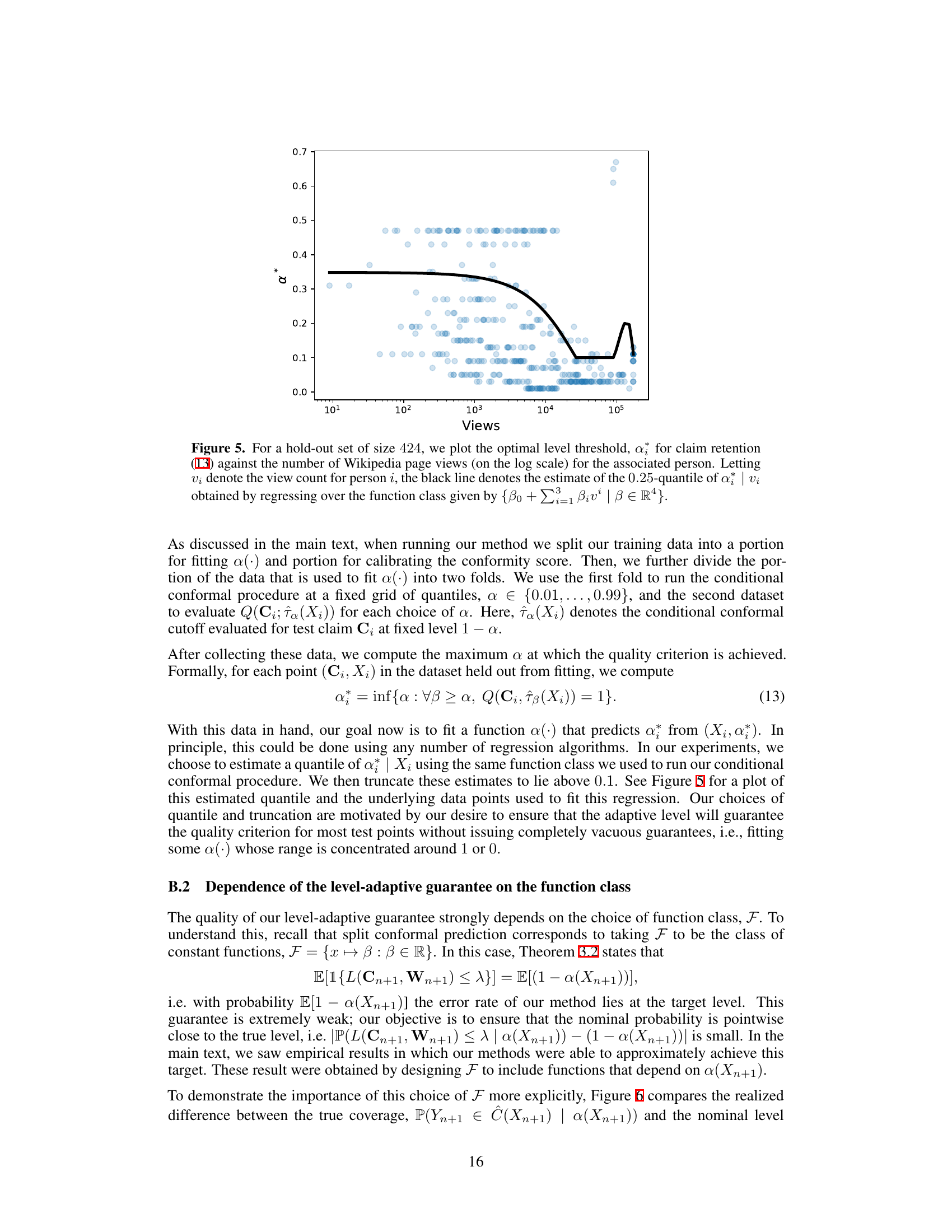
This figure shows the relationship between the optimal level threshold (α*) for claim retention and the number of Wikipedia page views for the associated person. The optimal α* is determined using a hold-out dataset of 424 data points. The black line represents the estimated 0.25-quantile of α given the number of views, obtained by regression analysis using a specific function class. The figure illustrates how the optimal threshold for claim retention adjusts based on the popularity (number of views) of the biographical subject.

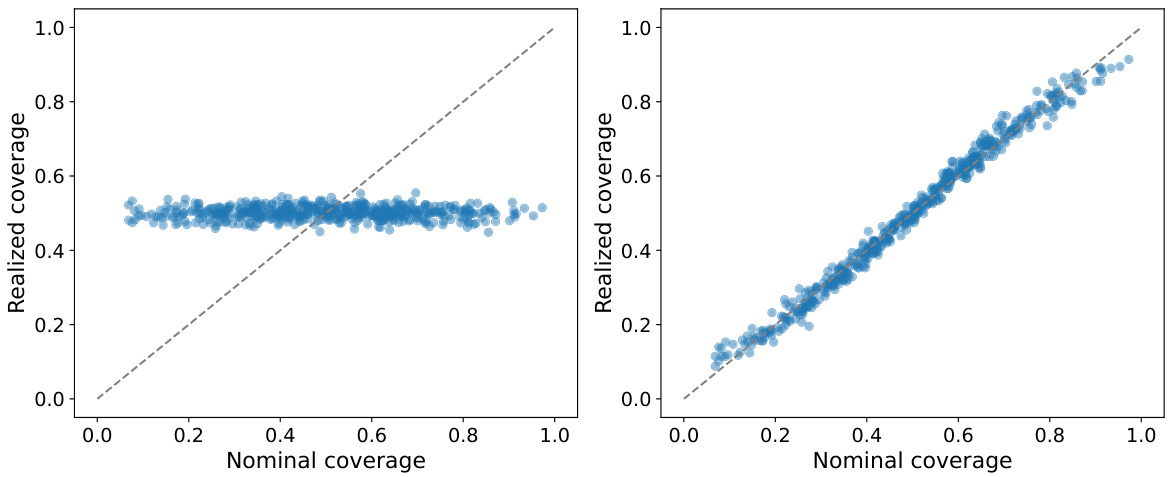
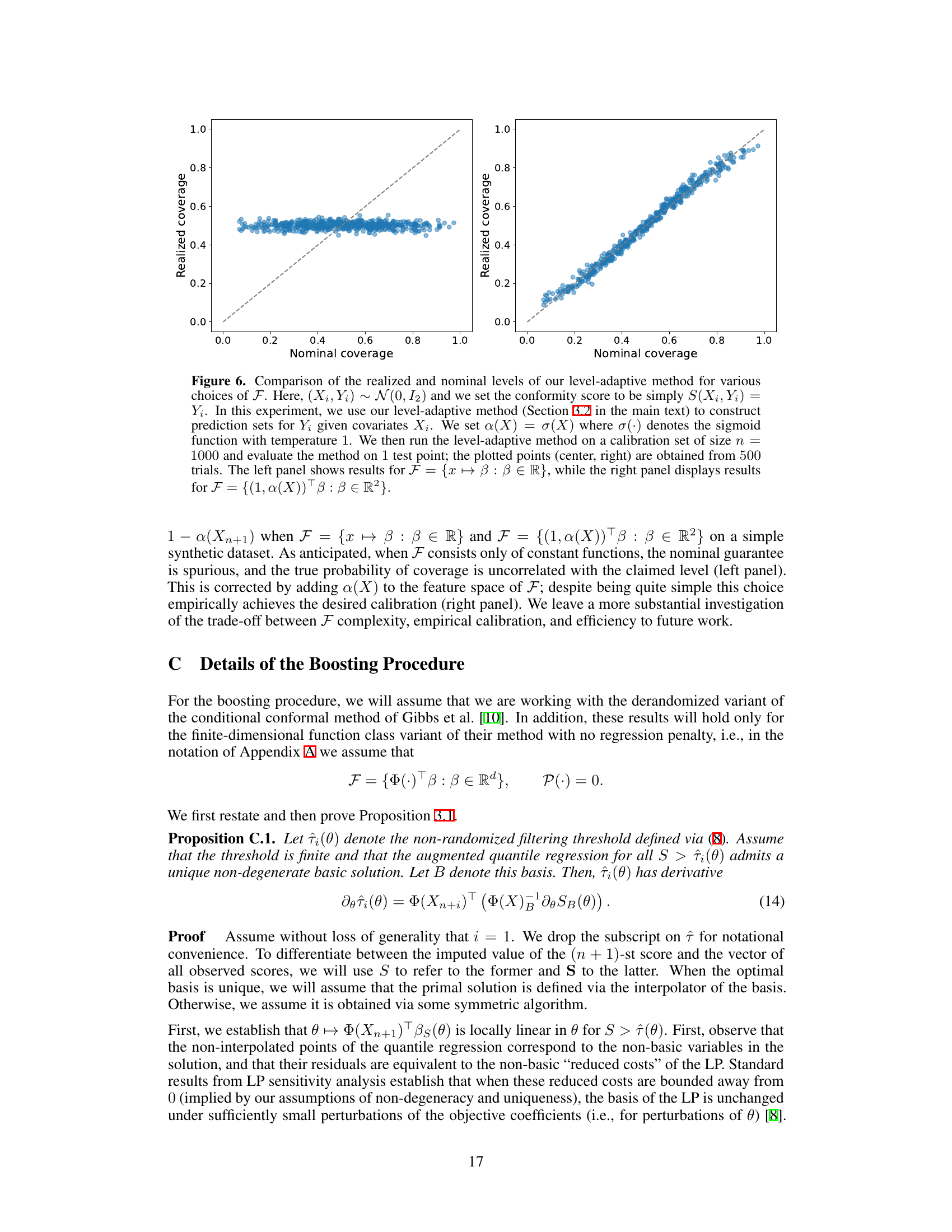
This figure compares the realized and nominal coverage levels of the level-adaptive conformal prediction method for two different choices of the function class F. The left panel shows results for F = {x ↔ β: β∈R} (constant functions), while the right panel shows results for F = {(1,α(X))Τβ: β∈R2}, which includes the adaptive level function a(X). The results demonstrate the importance of choosing a sufficiently rich function class F to achieve good calibration.

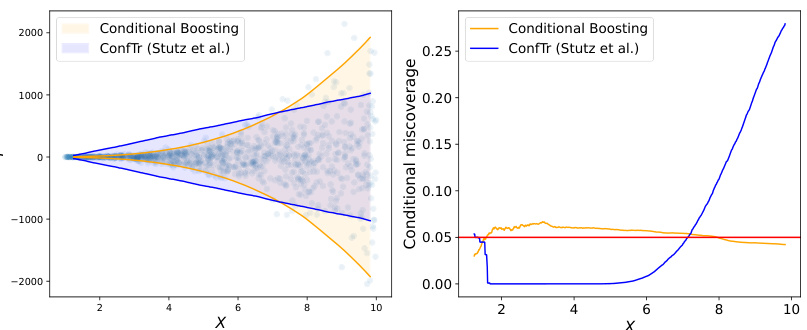
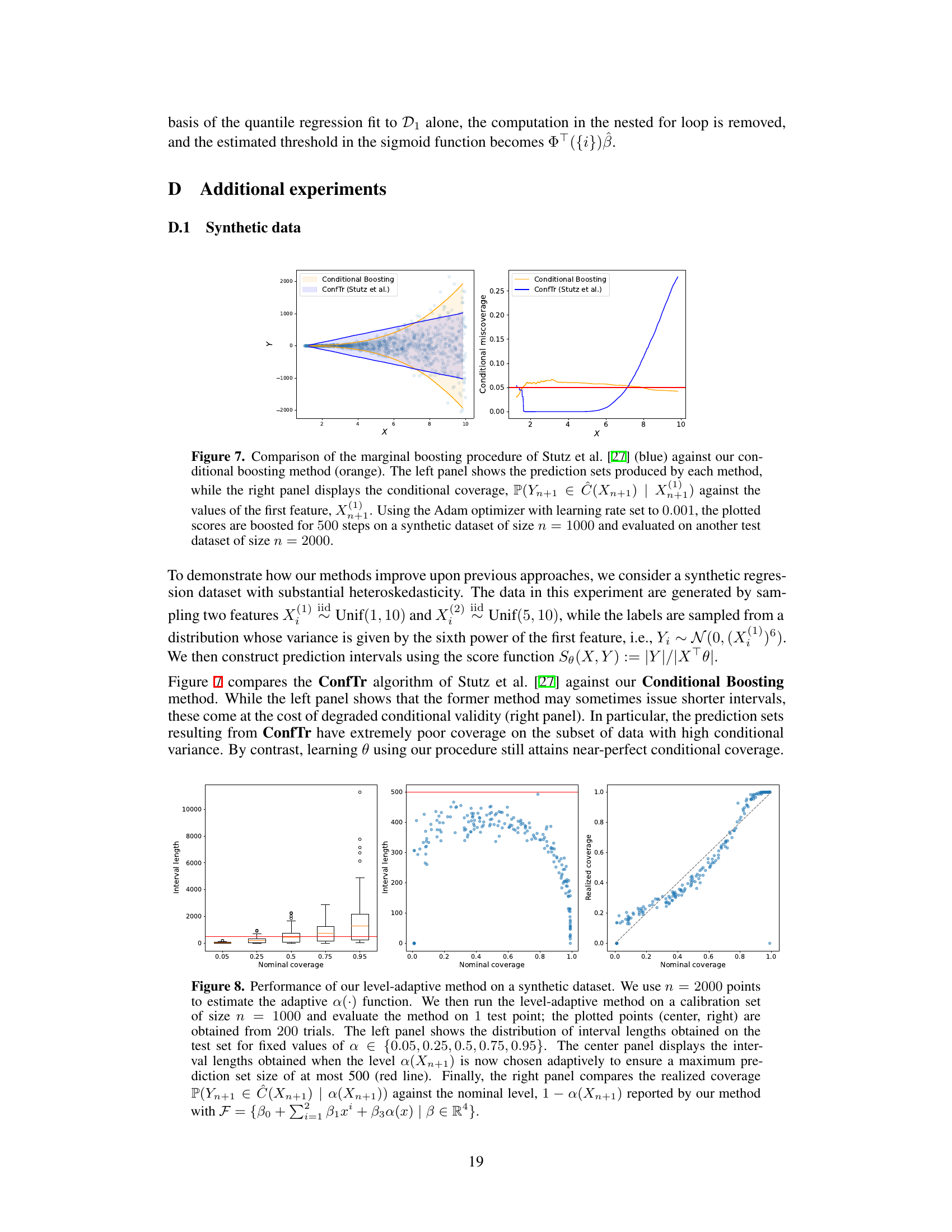
This figure compares the performance of the authors’ conditional boosting method against the marginal boosting method of Stutz et al. [27] on synthetic data. The left panel visually shows the prediction intervals generated by each method, illustrating the difference in their coverage. The right panel plots the conditional coverage (the probability that the true value falls within the prediction interval given the value of the first feature, X(1)) against the value of X(1). This demonstrates how the conditional coverage varies across different values of X(1) for both methods, highlighting the superiority of the authors’ approach in maintaining consistent conditional coverage.

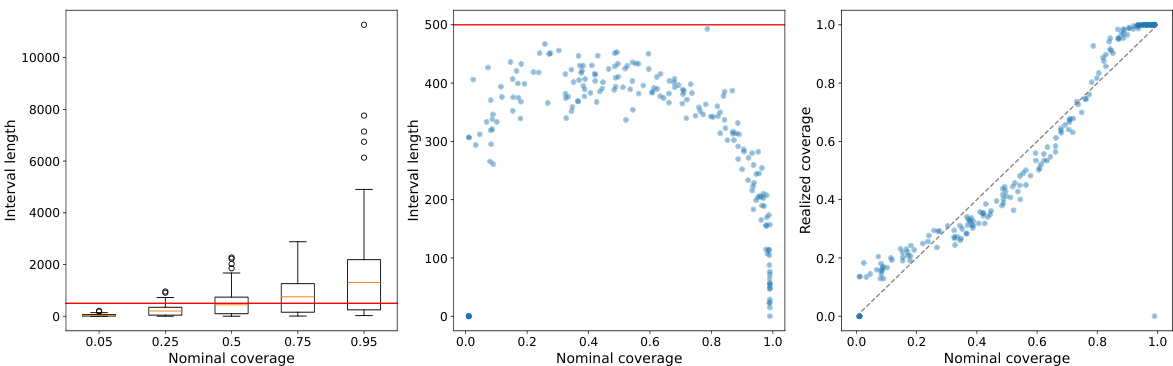
This figure shows the result of applying the level-adaptive conformal prediction method on a synthetic dataset. The left panel illustrates the distribution of interval lengths for various fixed nominal coverage levels. The middle panel demonstrates the effect of adaptively choosing the level to control the maximum interval length. The right panel displays the calibration of the method by comparing the realized and nominal coverage levels.

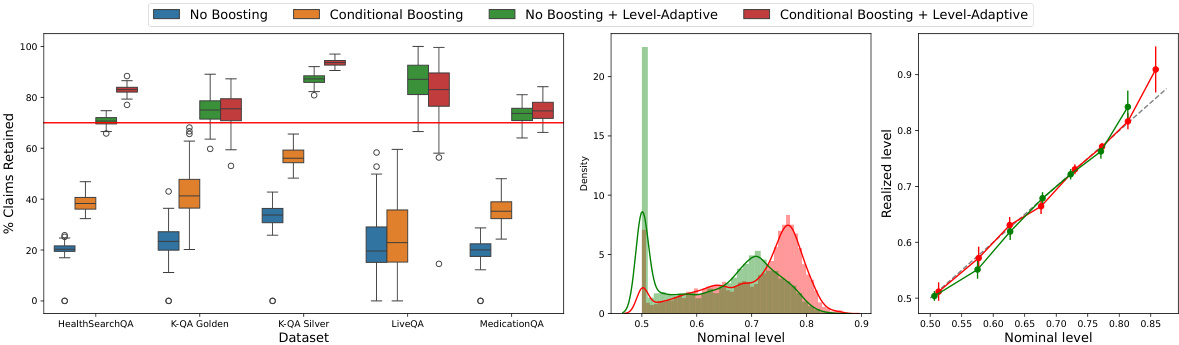
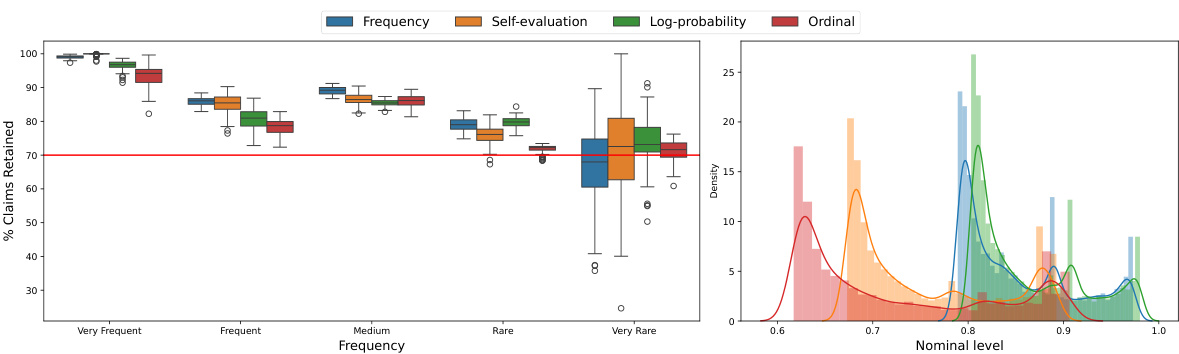
This figure empirically demonstrates the effectiveness of the proposed conditional boosting and level-adaptive methods on several datasets for medical question answering. The left panel shows the calibration of the model’s nominal factuality probabilities against realized probabilities (estimated from 500 test points and 100 calibration-test splits). The right panel compares the claim retention rates of the proposed methods against the baseline method, showcasing the improved performance of the proposed methods.

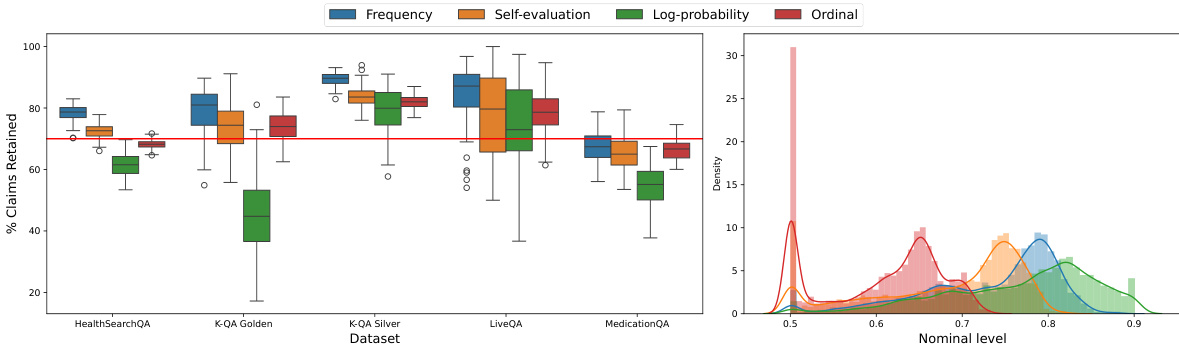
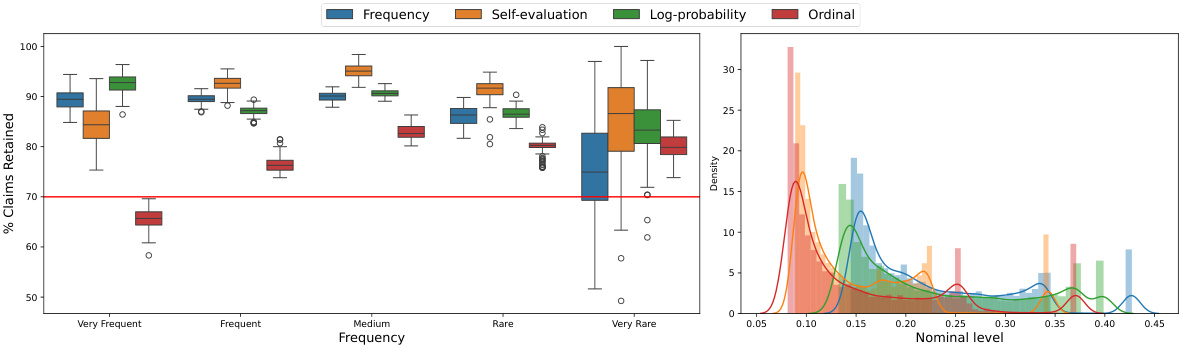
This figure empirically demonstrates the effectiveness of the proposed conditional boosting and level-adaptive methods. The left panel shows the calibration of the method, comparing nominal and realized factuality probabilities across different confidence levels. The right panel compares claim retention rates across various methods (unboosted scores, boosted scores, and boosted scores with level adaptation), highlighting the improved claim retention achieved by the proposed methods while maintaining factuality guarantees.

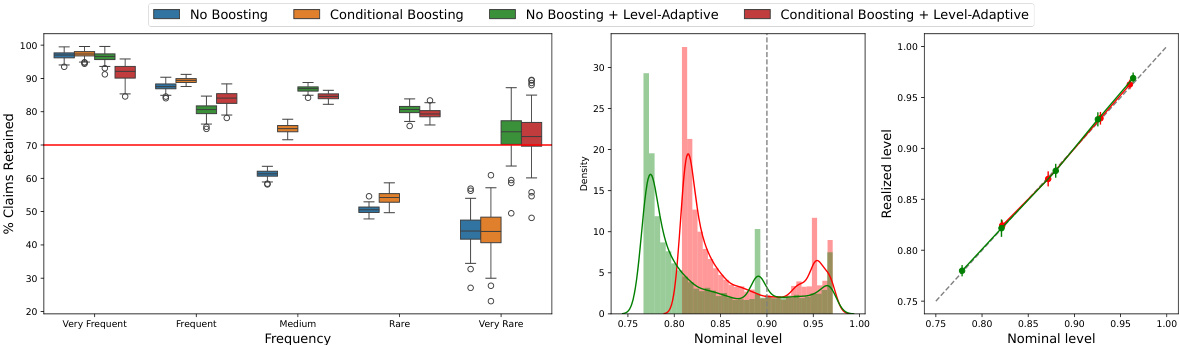
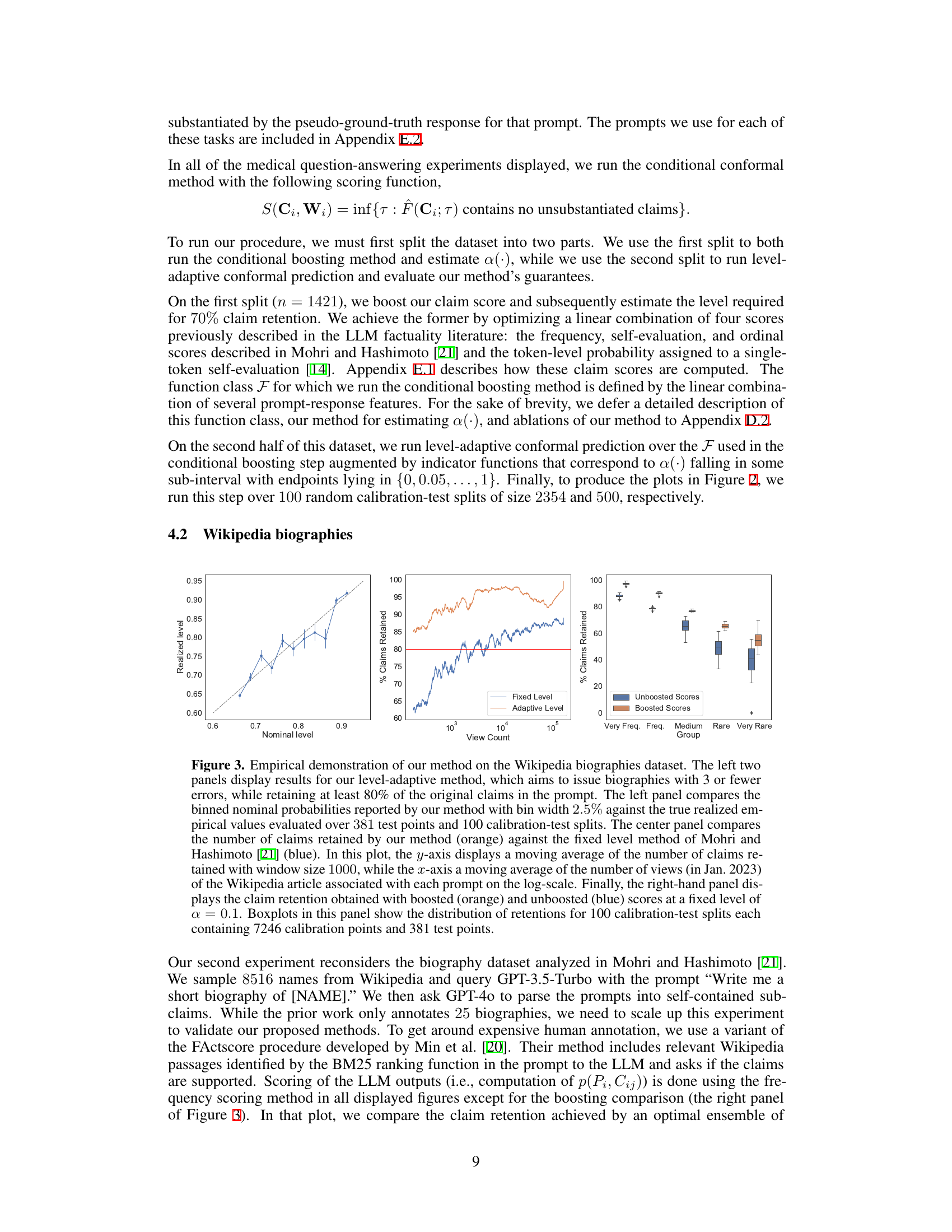
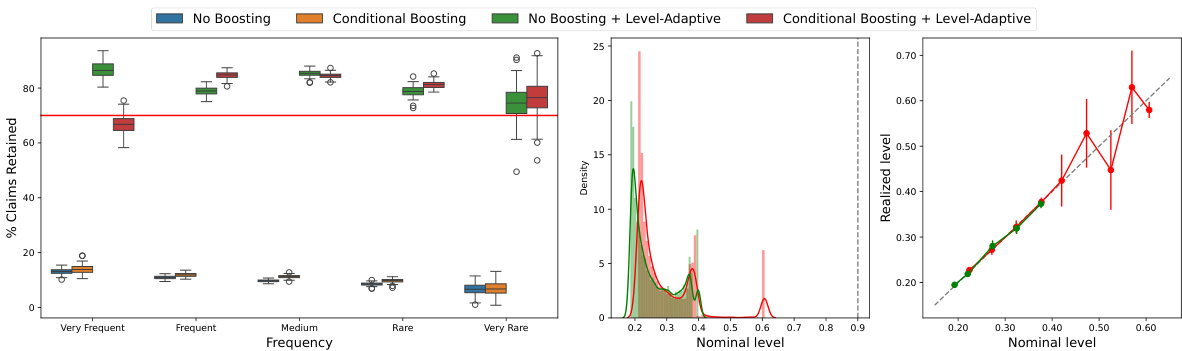
This figure compares four different claim filtering methods on the MedLFQA benchmark dataset. The methods vary in whether they use boosting and/or an adaptive level for the conformal prediction. The left panel shows the percentage of claims retained by each method, the middle panel demonstrates the impact of boosting on the level-adaptive method’s confidence, and the right panel verifies the calibration of the reported probability levels.

This figure empirically demonstrates the performance of conditional boosting and level-adaptive methods on six datasets. The left panel shows the calibration of the method; the nominal probability of factuality closely matches the realized probability. The right panel compares the claim retention across various methods, with conditional boosting showing significant improvement in the percentage of claims retained.

This figure empirically demonstrates the performance of the proposed conditional boosting and level-adaptive methods. The left panel shows the calibration of the method, comparing the nominal (expected) factuality probabilities to the realized (actual) probabilities across different confidence levels. The right panel compares the claim retention rates (percentage of original claims kept after filtering) of three methods: unboosted scores, boosted scores, and boosted scores with level adaptation. The results show that the proposed methods improve both the calibration and claim retention compared to the baseline.

This figure empirically demonstrates the performance of the proposed conditional boosting and level-adaptive conformal prediction methods. The left panel shows the calibration of the method, comparing the predicted probability of factuality to the actual realized probability. The right panel compares the claim retention rate of the proposed methods against a baseline method, highlighting the improvement achieved by incorporating boosting and adaptive level selection.

Full paper

#