Binary Search with Distributional Predictions

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in algorithms and machine learning because it bridges the gap between theoretical worst-case algorithms and the probabilistic nature of modern machine learning predictions. It introduces a novel framework for designing algorithms that effectively utilize distributional predictions, leading to improved efficiency and robustness. This opens new avenues for research in algorithm design, especially in areas where predictions are inherently probabilistic, offering significant improvements over existing point-prediction approaches.

Visual Insights

#

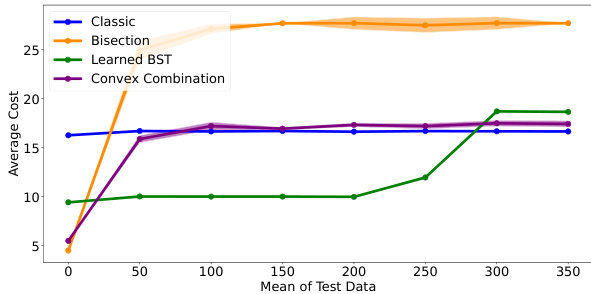
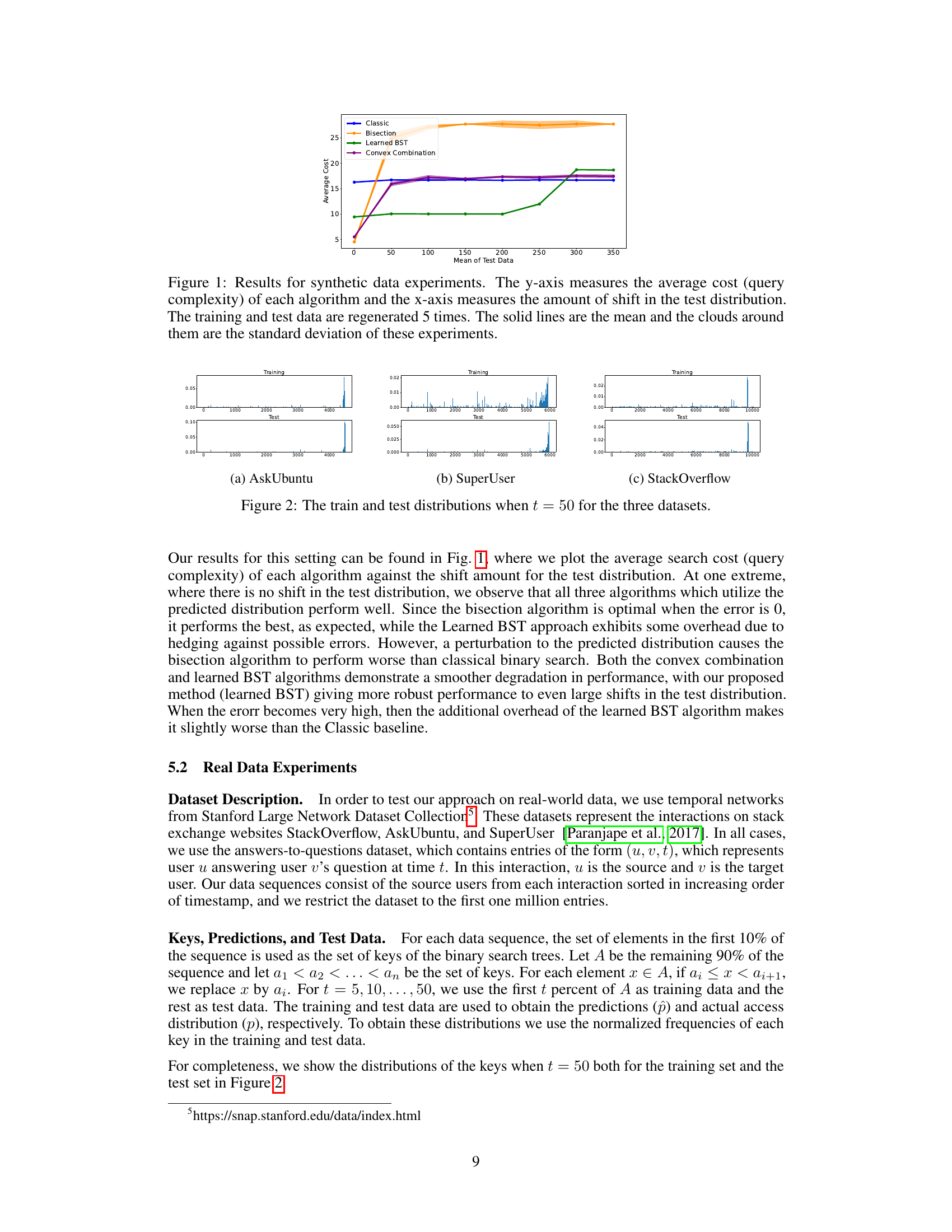
This figure shows the results of synthetic data experiments comparing four different search algorithms: Classic, Bisection, Learned BST, and Convex Combination. The y-axis represents the average cost (number of queries) of each algorithm, while the x-axis shows the mean of the test data distribution, representing the amount of shift from the training data distribution. The plot demonstrates how the performance of each algorithm varies with the difference between the training and testing distributions. The solid lines indicate the average cost, and the shaded areas represent the standard deviation, showing the variability of the results across five repetitions of the experiment.

In-depth insights

#

Distrib. Robustness

#

The concept of “Distributional Robustness” in the context of the provided research paper centers on the ability of an algorithm to perform well even when the predicted distribution of data differs from the true distribution. The core challenge is that machine learning models often output probability distributions as predictions, yet most existing algorithms assume point predictions. The paper directly addresses this gap, focusing on the fundamental problem of binary search in a sorted array. It demonstrates that naively converting a distributional prediction to a single point estimate can lead to suboptimal performance. Instead, the authors propose an algorithm that leverages the entire predicted distribution effectively to achieve near-optimal query complexity, offering a crucial robustness against prediction error measured by the Earth Mover’s Distance (EMD). This robustness extends to the related problem of constructing optimal binary search trees (BSTs), providing a significant advancement in algorithm design with distributional predictions.

Algo. Complexity

#

The algorithm’s complexity is a central theme, focusing on query complexity—the number of comparisons needed to find a target key. The paper cleverly interweaves traditional binary search with a median-finding approach based on the predicted distribution. The resulting query complexity is shown to be O(H(p) + log n), where H(p) is the entropy of the true distribution and n is the Earth Mover’s Distance (EMD) between the predicted and true distributions. This bound highlights the algorithm’s robustness; if the prediction is accurate (n is small), the complexity approaches the information-theoretic lower bound H(p). If the prediction is poor, it gracefully degrades to the O(log n) complexity of standard binary search. A lower bound of Ω(H(p) + log n) is also proven, demonstrating the essential optimality of the algorithm. The algorithm’s adaptability to multiple predictions is also explored, maintaining near-optimal performance. The analysis rigorously considers both average and worst-case scenarios, providing strong theoretical guarantees.

Point Prediction?

#

The subheading “Point Prediction?” in the context of a research paper on algorithms with distributional predictions immediately highlights a critical methodological question. The core issue is whether simplifying a probability distribution (inherent in machine learning predictions) into a single point estimate is sufficient for optimizing algorithm performance. The inherent loss of information when moving from a distribution to a single point is the central concern. The paper likely explores various point prediction methods (e.g., mean, median, mode, maximum likelihood estimate) and assesses their efficacy in a binary search context, comparing them to algorithms that directly utilize the entire distribution. A key finding might be a demonstration that the performance of algorithms based on point predictions is significantly suboptimal compared to those using distributional information, especially when considering the robustness against prediction errors. This section would likely provide a formal analysis and potentially experimental results supporting this conclusion, emphasizing the advantages of leveraging the full distributional prediction, and justifying the need for developing and analyzing algorithms designed to handle distributional inputs directly.

Empirical Studies

#

A hypothetical ‘Empirical Studies’ section in a research paper on algorithms with distributional predictions would likely present a systematic evaluation of the proposed algorithm’s performance. This would involve carefully designed experiments using both synthetic and real-world datasets. The synthetic data would allow for controlled manipulation of key parameters, such as the accuracy of predictions and the underlying data distribution, to isolate the effects of these factors on the algorithm’s efficiency. Real-world datasets, on the other hand, would provide a more realistic evaluation, highlighting the algorithm’s practical performance in diverse scenarios. Key metrics of success might include query complexity (number of comparisons), runtime, and robustness to prediction errors. A comparison against baseline algorithms such as traditional binary search and algorithms employing point predictions would be crucial to demonstrate the practical advantages of using distributional predictions. The results section would thoroughly document the findings, potentially including visual aids like graphs, to highlight the algorithm’s strengths and limitations. A thoughtful discussion of the results would be essential, exploring any unexpected behaviors or anomalies and proposing avenues for future research.

Future Research

#

Future research directions stemming from this work on binary search with distributional predictions are plentiful. Extending the algorithm to more complex search structures beyond sorted arrays, such as trees or graphs, would be a significant advancement. This would require careful consideration of how distributional predictions translate to these more intricate structures and how to maintain optimality. Investigating alternative distance metrics beyond Earth Mover’s Distance (EMD) to measure the discrepancy between predicted and true distributions is crucial, especially metrics less sensitive to support mismatches. Furthermore, exploring the impact of prediction quality—quantified by measures like entropy and divergence—on the algorithm’s performance requires a deeper theoretical analysis. Developing algorithms that efficiently handle multiple, potentially conflicting, distributional predictions (prediction portfolios) is another promising direction. Finally, applying this framework to other fundamental algorithmic problems beyond search, such as sorting or selection, and evaluating the empirical performance gains on real-world datasets will prove highly valuable.

More visual insights

#

More on figures

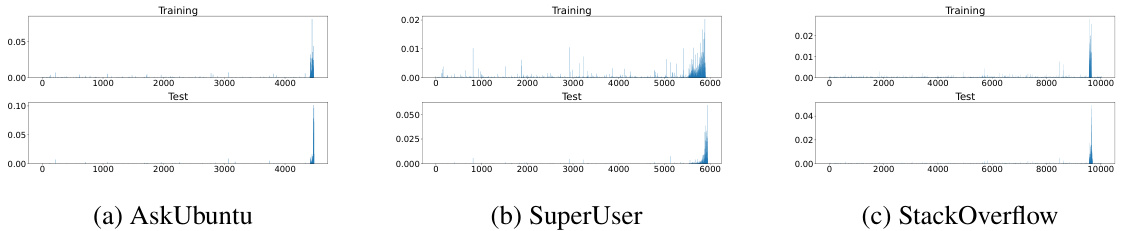
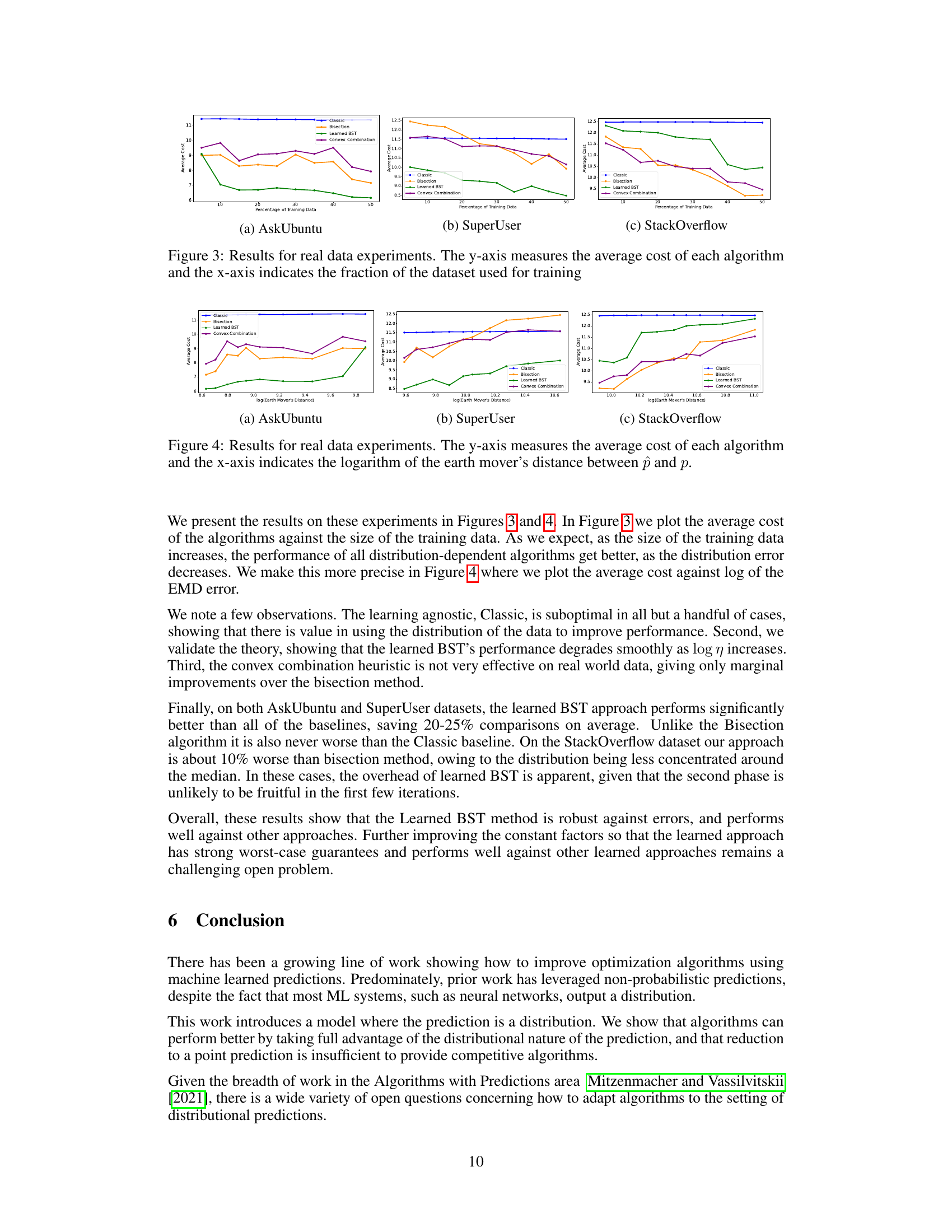
This figure shows the training and testing data distributions for three different datasets (AskUbuntu, SuperUser, and StackOverflow) when 50% of the data is used for training. The distributions are visualized as histograms, illustrating the frequency of different keys in the training and testing sets for each dataset. The purpose is to demonstrate the similarity and differences between the training and testing distributions for each dataset, indicating how well the training data represents the test data.

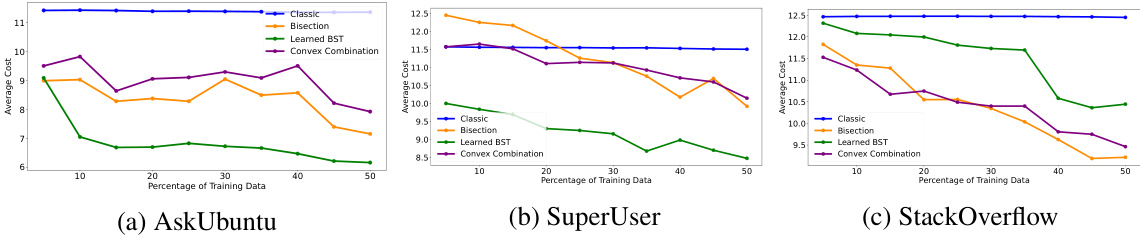
This figure shows the results of real data experiments comparing the performance of four different algorithms: Classic, Bisection, Learned BST, and Convex Combination. The y-axis represents the average cost (likely number of queries or comparisons) of each algorithm, while the x-axis shows the percentage of the dataset used for training the prediction model. The graph displays how the average cost changes as more training data is used. This visualization helps to understand the impact of training data size on the performance of each algorithm in a real-world setting.

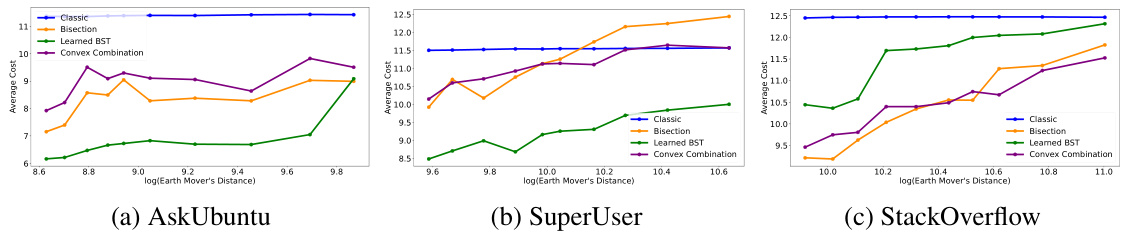
This figure shows the performance of four different algorithms (Classic, Bisection, Learned BST, and Convex Combination) on three real-world datasets (AskUbuntu, SuperUser, and StackOverflow). The y-axis represents the average cost (number of queries) of each algorithm, and the x-axis represents the logarithm of the Earth Mover’s Distance (EMD) between the predicted distribution ( p̂ ) and the true distribution (p). The plots illustrate how the average cost changes as the accuracy of the predicted distribution varies, showcasing the robustness and efficiency of the proposed Learned BST algorithm compared to other methods. The results demonstrate that the Learned BST algorithm exhibits a smoother degradation in performance as the EMD increases, remaining competitive even when the prediction accuracy is low.

Full paper

#