↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world applications involve multimodal data (e.g., images, text, and sensor readings) which often contains missing data and irregular time sampling patterns. Successfully integrating and utilizing such data is critical, yet challenging. Existing methods either fail to incorporate such irregularities or struggle with scalability when handling a diverse range of modalities.
The proposed FuseMoE framework utilizes a mixture-of-experts approach with a novel Laplace gating function to effectively integrate diverse modalities. This design addresses the limitations of existing methods by efficiently managing missing data and irregular temporal patterns. FuseMoE’s unique gating function theoretically enhances convergence speed and practically yields superior performance in numerous downstream prediction tasks. Empirical evaluations across diverse datasets demonstrate the effectiveness and adaptability of the framework in real-world scenarios.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers dealing with multimodal data, particularly in fields like healthcare. It provides a novel framework to handle data with missing values and irregular sampling, improving predictive performance and opening new avenues for research in this challenging domain.
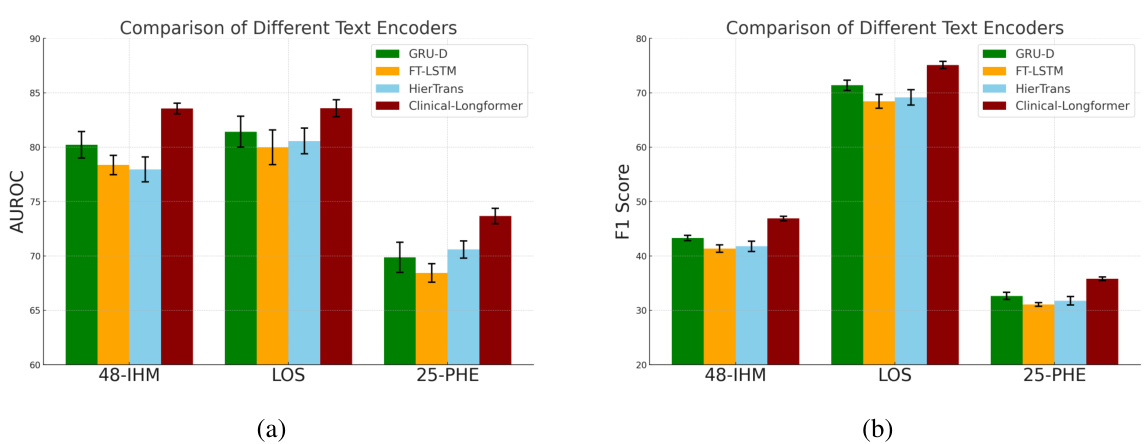
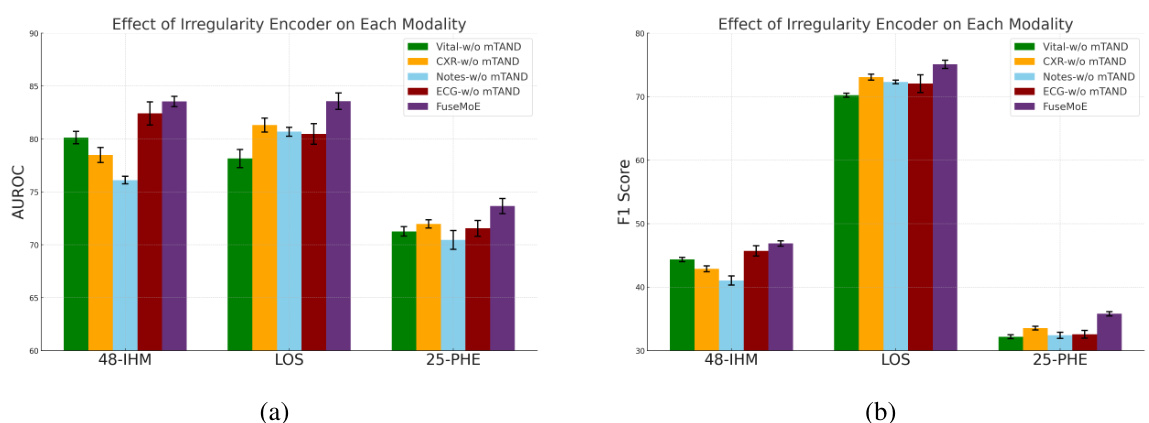
Visual Insights#
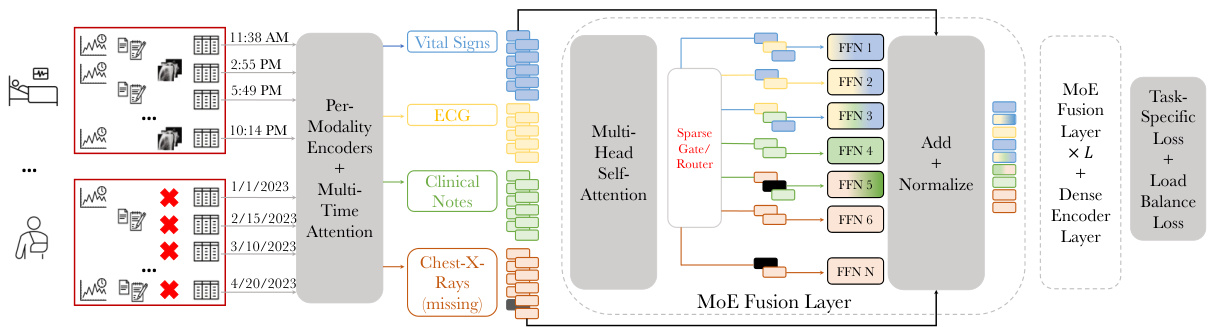
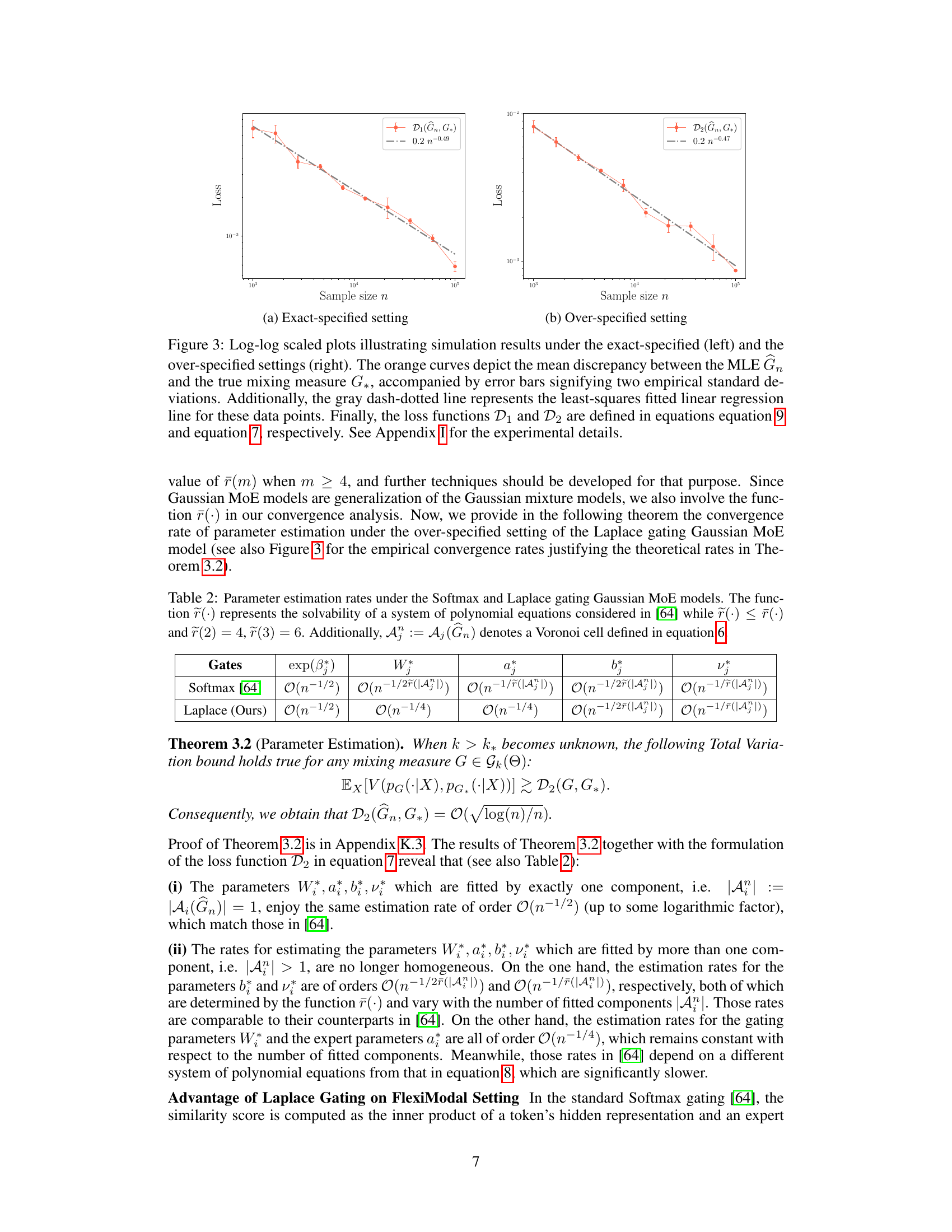
This figure illustrates the FuseMoE architecture for handling FlexiModal data. It shows how modality-specific encoders process various data types (vital signs, ECG, clinical notes, chest X-rays), handling missing data and irregular sampling. A multi-time attention mechanism addresses temporal irregularities. The core is the MoE Fusion Layer, routing data to expert MLPs based on a gating function, producing fused embeddings for downstream tasks.

This table compares FuseMoE with other state-of-the-art multimodal fusion methods. It highlights key differences in their ability to handle irregular data, missing modalities, and varying numbers of modalities. The table also notes whether each method has a theoretical foundation and if it’s adaptable to the FlexiModal data setting (FuseMoE’s focus).
In-depth insights#
Fleximodal Fusion#
Fleximodal fusion, as discussed in the research paper, tackles the challenges of integrating diverse data modalities—often incomplete and irregularly sampled—for enhanced predictive performance. The core concept revolves around handling the variability in the number and types of modalities, moving beyond simple pairwise comparisons and concatenation. This is accomplished through a novel framework that leverages a mixture-of-experts (MoE) architecture with a specially designed gating function. This allows for scalable and flexible integration of various modalities, adapting to missing data by dynamically adjusting the influence of experts. The unique Laplace gating function is shown to theoretically offer enhanced convergence and predictive performance compared to traditional softmax gating. The real-world applicability is validated through various experimental evaluations, showcasing its effectiveness in handling scenarios with missing data and irregular sampling, often encountered in real-world applications like healthcare.
MoE Framework#
The MoE framework, as described in the research paper, is a powerful method for handling the complexities of multimodal data, especially in scenarios with missing or irregularly sampled data. Its core innovation lies in the use of a sparse mixture-of-experts architecture, where each expert specializes in processing a specific modality or subset of modalities. This allows for efficient and scalable handling of a large number of input modalities and makes it highly adaptive to situations where certain modalities might be missing. The gating mechanism plays a critical role in this framework, intelligently routing each input to the most appropriate experts for that specific input. The paper proposes a novel Laplace gating function, theoretically demonstrating improved convergence rates over traditional Softmax gating, leading to enhanced performance. The incorporation of a modality and irregularity encoder further enhances the effectiveness of the MoE framework. This approach tackles the challenges of diverse data types and temporal irregularities, making it robust and suitable for handling complex real-world data such as electronic health records. The efficacy of the MoE fusion layer is empirically validated through multiple real-world applications, showcasing its superior predictive performance compared to state-of-the-art baseline methods.
Laplace Gating#
The proposed Laplace gating mechanism offers a compelling alternative to the commonly used softmax gating in Mixture-of-Experts (MoE) models. Its core innovation lies in substituting the softmax function with a Laplace distribution-based gating function. This seemingly simple change yields significant theoretical and practical advantages. Theoretically, the Laplace gating function is shown to improve convergence rates in maximum likelihood estimation, leading to more efficient model training. Empirically, the paper demonstrates improved predictive performance across a variety of challenging tasks, especially in scenarios with FlexiModal data. The bounded nature of the Laplace function helps prevent the representation collapse often observed in softmax gating, where a few experts dominate the model’s output. This improved stability likely contributes to its superior performance. The authors further showcase the Laplace gating function’s robustness in handling missing or irregular data, which is a critical advantage in real-world applications such as healthcare. The superior performance of Laplace gating is not only an empirical observation but also supported by theoretical guarantees on convergence rates, making it a promising technique for enhancing the effectiveness of MoE models in diverse applications.
EHR Analyses#
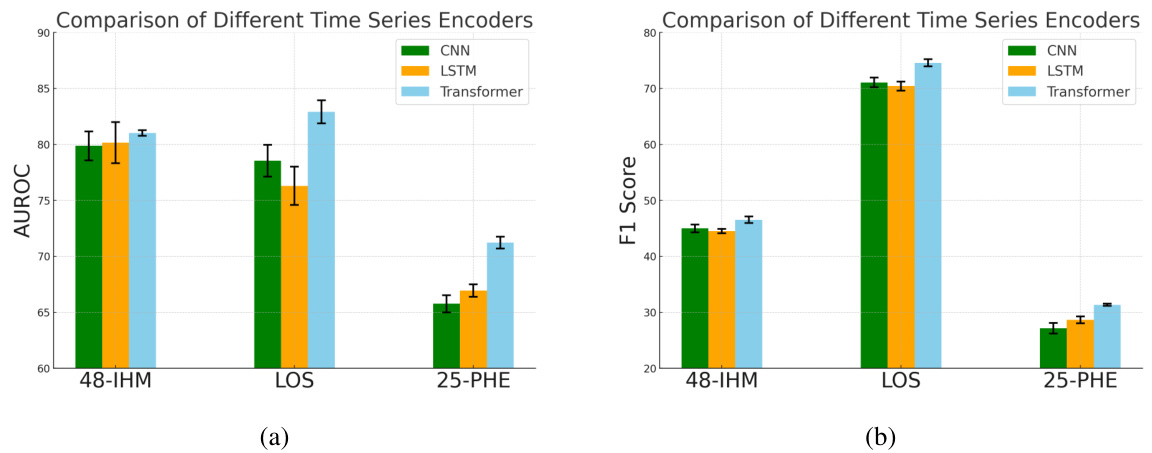
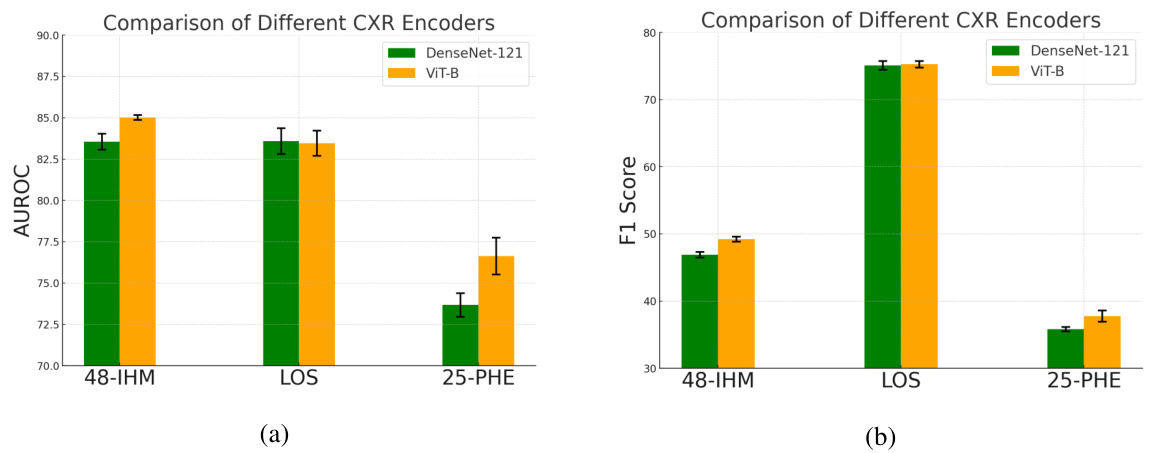
EHR analysis in healthcare research involves extracting valuable insights from electronic health records to improve patient care and advance medical knowledge. This process often requires careful consideration of data privacy, ensuring compliance with regulations like HIPAA. Data preprocessing is crucial, involving cleaning, standardization, and handling of missing or incomplete data. Various analytical techniques are then applied, ranging from simple descriptive statistics to complex machine learning algorithms. Key tasks in EHR analysis include identifying risk factors for specific diseases, predicting patient outcomes, and personalizing treatment plans. Challenges include data heterogeneity, variability in data quality, and the need for scalable solutions to handle massive datasets. The results of EHR analysis can be used to inform clinical decision-making, develop new treatment strategies, and monitor the effectiveness of interventions. Ethical considerations are paramount, particularly regarding the use of sensitive patient information. Ultimately, EHR analysis is a powerful tool with the potential to greatly enhance the quality and efficiency of healthcare, but its use must be carefully managed to ensure responsible and ethical application.
Future Works#
The research paper’s ‘Future Works’ section would ideally explore several avenues. Extending FuseMoE’s capabilities to handle even more diverse modalities is crucial. This could involve incorporating additional data types, such as wearable sensor data or genomic information, to further enhance its predictive power in complex, real-world scenarios. Investigating alternative gating mechanisms, beyond the proposed Laplace and Softmax functions, could potentially improve convergence speed and robustness. A thorough investigation into the theoretical properties of the Laplace gating function would provide a stronger mathematical foundation and guide further optimization efforts. Developing more efficient methods for encoding irregular and missing data is also critical, as current methods might over-parameterize for smaller datasets. Finally, comprehensive testing and validation on a larger scale, with a more extensive range of FlexiModal datasets, would solidify the practical impact and generalizability of the FuseMoE model. Benchmarking against other state-of-the-art multimodal fusion methods in various domains would further establish its superiority.
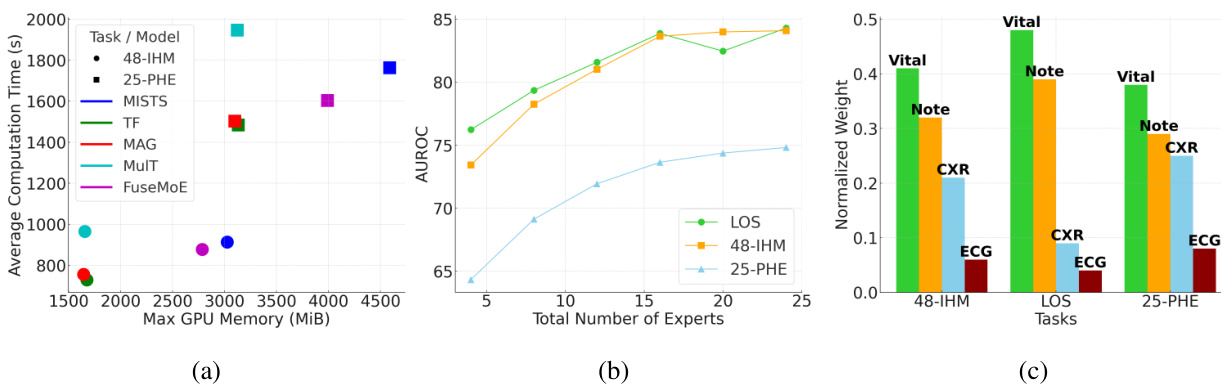
More visual insights#
More on figures

This figure illustrates three different architectures for the Top-K router in a multimodal fusion model. The designs explore different strategies for combining and routing modalities to expert networks. (a) shows a joint router approach, where a single router processes the concatenated embeddings of all modalities. (b) shows a per-modality router, where separate routers process each modality’s embedding individually and share a common pool of experts. (c) demonstrates disjoint experts and routers, where separate routers route each modality to unique and separate pools of experts.
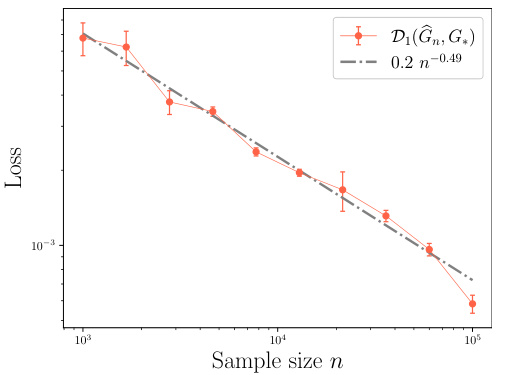
This figure shows the results of simulation experiments to compare the convergence rates of maximum likelihood estimation (MLE) under the Laplace gating and the Softmax gating in Gaussian Mixture of Experts model. The left panel shows the results under the exact-specified setting where the number of experts is known, while the right panel shows the results under the over-specified setting where the number of experts is unknown. The plots show the mean discrepancy between the MLE and the true mixing measure, along with error bars representing the empirical standard deviations. The gray dash-dotted lines represent the least-squares fitted linear regression line for the data. The convergence rates are indicated in the legend. Appendix I provides additional details about the experimental setup.

This figure shows the results of simulation experiments comparing the maximum likelihood estimation (MLE) under the Laplace gating and Softmax gating in the mixture-of-experts (MoE) model. The left panel shows the results under the exact-specified setting (when the true number of experts is known), while the right panel shows the results under the over-specified setting (when the true number of experts is unknown). The orange curves represent the mean discrepancy between the MLE and the true mixing measure, with error bars showing the two empirical standard deviations. The gray dash-dotted lines show the least-squares fitted linear regressions. The loss functions D1 and D2 are defined in equations (7) and (9), respectively.
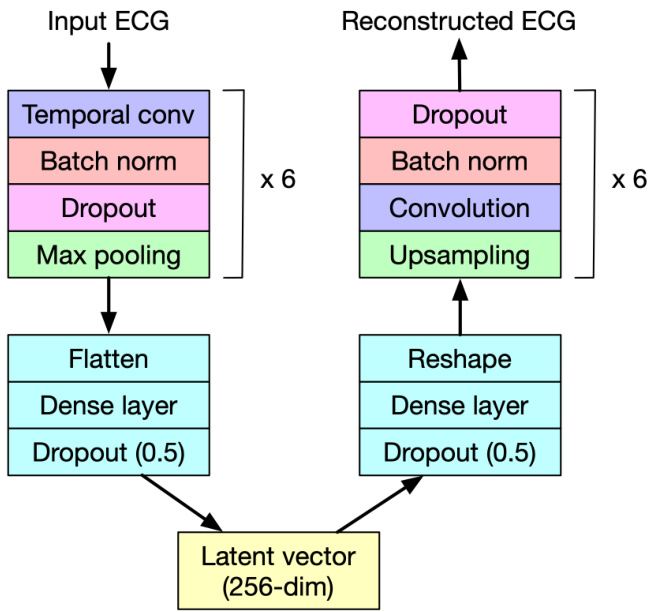
This figure illustrates how FuseMoE handles Fleximodal data, characterized by a variable number of modalities and irregular sampling patterns. It shows how modality-specific encoders process different data types (vital signs, ECG, clinical notes, etc.), with a multi-time attention mechanism addressing temporal irregularities. A gating function in the MoE Fusion Layer routes the data to appropriate experts for processing, ultimately generating fused embeddings for downstream tasks.

This figure illustrates how FuseMoE handles FlexiModal data, which is characterized by multiple modalities (vital signs, ECG, clinical notes, etc.), temporal irregularity, and missing data. FuseMoE first encodes each modality separately, uses multi-time attention to handle the irregular time series, and then employs a mixture-of-experts (MoE) fusion layer with a novel gating function to combine the information from all modalities, creating a final embedding for downstream tasks.
This figure illustrates the FuseMoE architecture and how it handles FlexiModal data, which is characterized by multiple modalities (vital signs, ECG, clinical notes, chest X-rays), irregular sampling, and missing data. FuseMoE leverages modality-specific encoders and a multi-time attention mechanism to manage irregular temporal dynamics and missingness. The core of the model is the MoE Fusion Layer, routing data to specialized experts (MLPs) based on a learned gating function, producing fused embeddings for downstream tasks.

This figure illustrates FuseMoE’s ability to handle FlexiModal data, which is characterized by diverse modalities, irregular sampling, and missingness. It shows the process of encoding different modalities using modality-specific encoders, handling temporal irregularities with a multi-time attention mechanism, and integrating them in the MoE fusion layer. The gating function routes the data to relevant experts for processing, producing fused embeddings for downstream tasks.
This figure illustrates the FuseMoE architecture and its ability to handle FlexiModal data (data with variable numbers of modalities, missing data, and irregular sampling). It shows how modality-specific encoders process different input types (vital signs, ECG, clinical notes, etc.), which are then integrated via a multi-time attention mechanism to account for irregular sampling patterns. Finally, a MoE fusion layer, guided by a novel gating function, combines the processed inputs into a fused embedding for downstream tasks.
This figure illustrates the FuseMoE architecture and how it handles FlexiModal data (data with multiple modalities, irregular sampling, and missing values). It shows how modality-specific encoders process different data types, a multi-time attention mechanism addresses temporal irregularities, and a Mixture-of-Experts (MoE) layer with a novel gating function fuses the information for prediction.
This figure illustrates FuseMoE’s architecture and how it handles FlexiModal data (data with multiple modalities, missing values, and irregular sampling). Modality-specific encoders process different data types, a multi-time attention mechanism addresses temporal irregularities, and a Mixture-of-Experts (MoE) fusion layer routes data to specialized experts based on input characteristics. The final embeddings are then used for prediction.
This figure illustrates the FuseMoE architecture and how it handles FlexiModal data, which is characterized by various modalities (vital signs, ECG, clinical notes, chest X-rays), temporal irregularity, and missing data. The architecture uses modality-specific encoders, followed by a multi-time attention mechanism and the core MoE fusion layer with a sparse gating mechanism to route inputs to the appropriate experts before producing fused embeddings.
This figure illustrates the FuseMoE architecture and its ability to handle FlexiModal data (data with varying numbers of modalities, missing data, and irregular sampling). It shows how modality-specific encoders process different data types, a multi-time attention mechanism addresses temporal irregularities, and a MoE fusion layer routes data to expert MLPs for weighted fusion and final embedding.

This figure illustrates the FuseMoE architecture and its ability to handle FlexiModal data, which is characterized by multiple modalities, temporal irregularity, and missing data. The architecture consists of modality-specific encoders, a multi-time attention mechanism, a MoE fusion layer, and a final prediction layer.
More on tables

This table compares FuseMoE against four benchmark methods across several characteristics: data type, handling of irregularity and missingness in data, number of modalities supported, theoretical analysis, and adaptability to FlexiModal data. It highlights FuseMoE’s unique advantages in handling complex, real-world multimodal data.

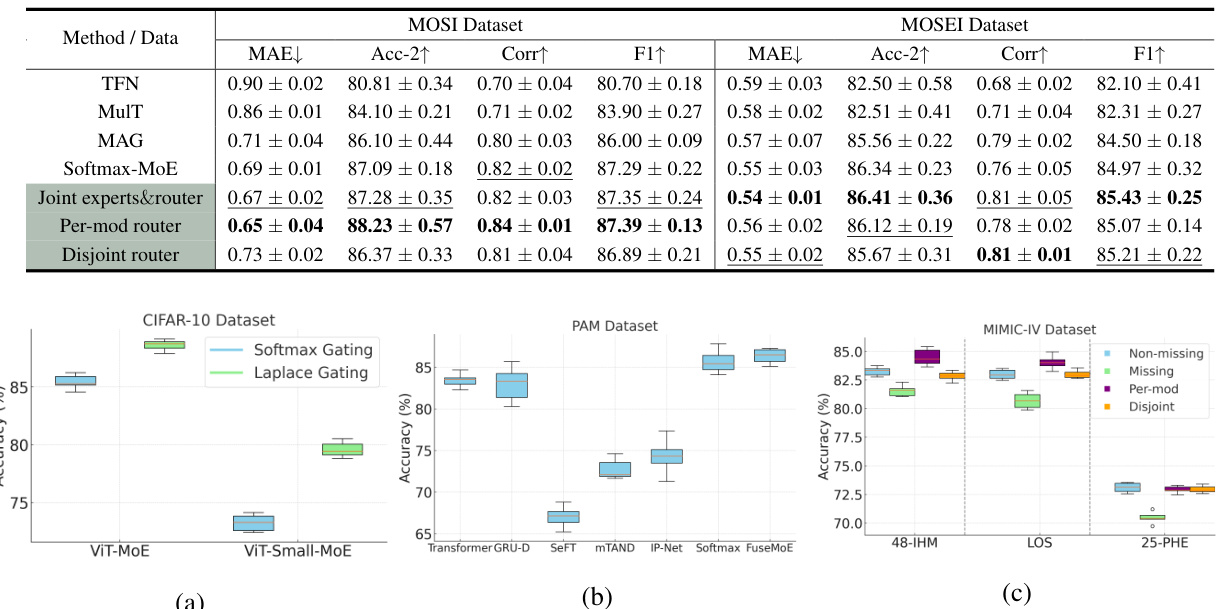
This table presents the results of the multimodal sentiment analysis experiments conducted on the CMU-MOSI and MOSEI datasets using several methods, including the proposed Mixture-of-Experts (MoE) approach. The table compares the performance of various methods across multiple metrics such as MAE (Mean Absolute Error), Accuracy, Correlation, and F1-score, highlighting the superior performance of the MoE approach. The results demonstrate that the MoE model offers better performance than existing methods when dealing with multimodal data in a sentiment analysis task.

This table presents the results of experiments comparing different methods on the CMU-MOSI and MOSEI datasets, focusing on the performance of MoE (Mixture-of-Experts). The table shows that MoE outperforms other methods in terms of accuracy, correlation, and F1-score. The results are averaged over 5 random experiments, and the best and second-best results are highlighted.
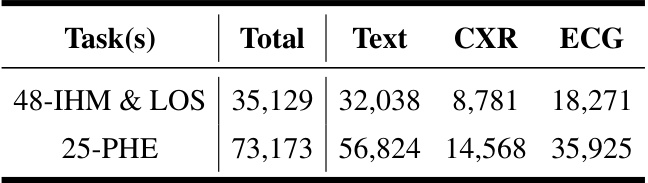
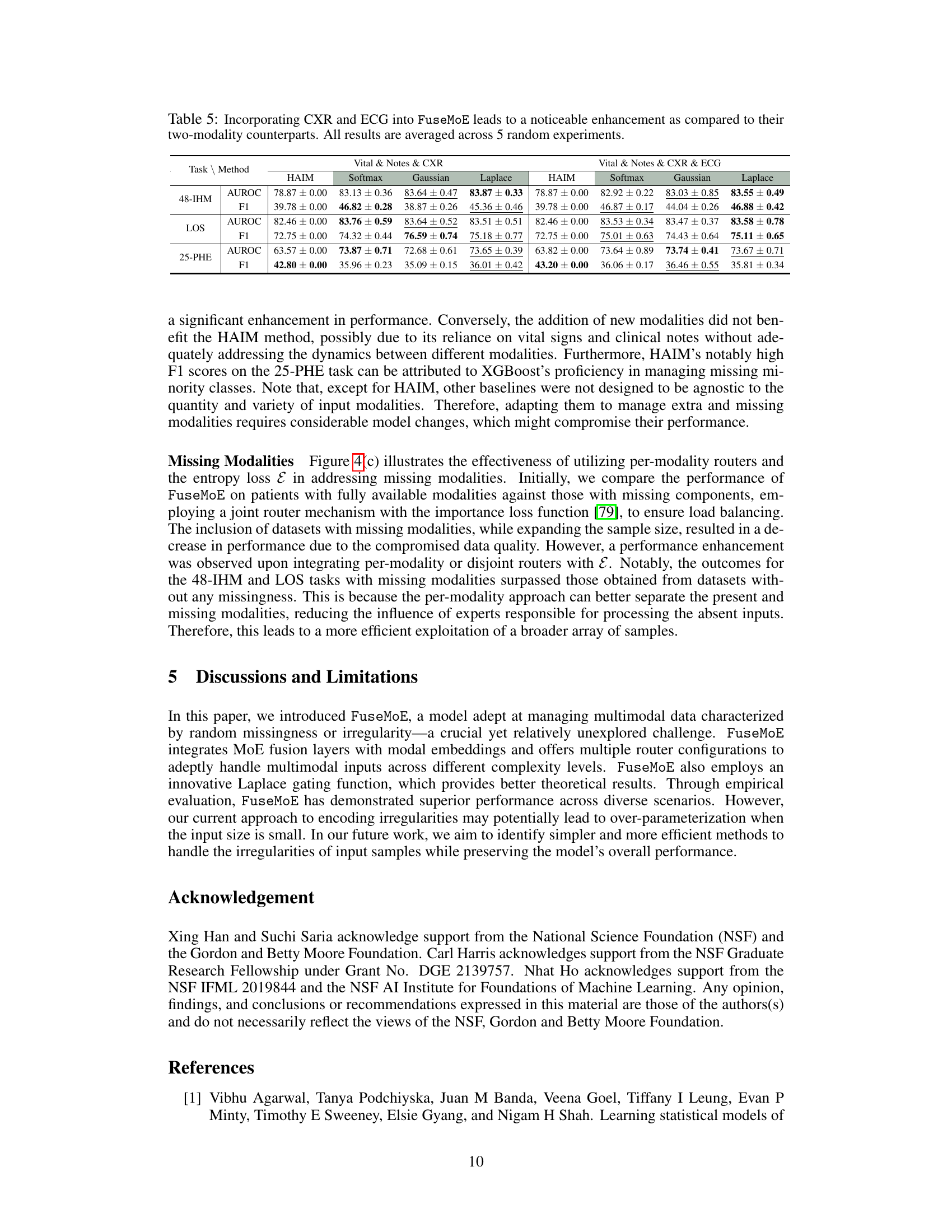
This table shows the number of ICU stays included in the study for three different tasks (48-IHM & LOS, 25-PHE). It also breaks down the total number of stays that had at least one observation for each modality (text, CXR, ECG). Note that missing modalities were considered in the total count, and this table helps show the prevalence of missing data in the different modalities.
This table presents a comparison of the performance of different methods on the CMU-MOSI and MOSEI datasets. The methods compared include various baselines (MulT, TFN, MAG) and different versions of the MoE model (Softmax-MoE, Joint experts&router, Per-mod router, Disjoint router). The metrics used for evaluation are MAE, Acc-2, Corr, and F1-score. The table shows that the MoE models, especially those with Laplace gating, consistently outperform the baselines across all metrics, highlighting the effectiveness of MoE in multimodal sentiment analysis.

This table compares the performance of different multimodal fusion methods on the CMU-MOSI and MOSEI datasets. The methods are evaluated based on several metrics, including MAE, Accuracy-2, Correlation, and F1-score. The table shows that the Mixture-of-Experts (MoE) approach outperforms other baseline methods across different metrics and datasets. The best results for each metric on each dataset are highlighted in bold font, with second best results underlined. This highlights the effectiveness of the MoE model, especially in handling multi-modal data.

This table presents the performance comparison of different methods on CMU-MOSI and MOSEI datasets. The metrics used include Mean Absolute Error (MAE), Accuracy-2 (Acc-2), Pearson Correlation (Corr), and F1-score. The table highlights the superior performance of the Mixture-of-Experts (MoE) model compared to baseline methods such as MulT, TFN, and MAG. Different MoE configurations (joint experts & router, per-modality router, disjoint router) are compared, showcasing the impact of architectural choices on performance.

This table presents a comparison of the performance of different methods on the CMU-MOSI and MOSEI datasets. The methods include several baselines and different versions of the MoE model, varying in their gating functions (Softmax, Laplace) and router designs. The performance metrics used include MAE, Acc-2 (accuracy), correlation (Corr), and F1-score. The best results for each metric are highlighted in bold, indicating that the MoE models generally outperformed the baselines.
Full paper#