Explicit Eigenvalue Regularization Improves Sharpness-Aware Minimization

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on generalization in deep learning because it offers a new theoretical understanding of Sharpness-Aware Minimization (SAM) and proposes Eigen-SAM, a more effective algorithm. Eigen-SAM directly tackles the limitations of SAM, opening avenues for improved model training and better generalization capabilities. The findings are particularly relevant to those exploring optimization algorithms, Hessian matrix analysis, and PAC-Bayes generalization bounds.

Visual Insights

#

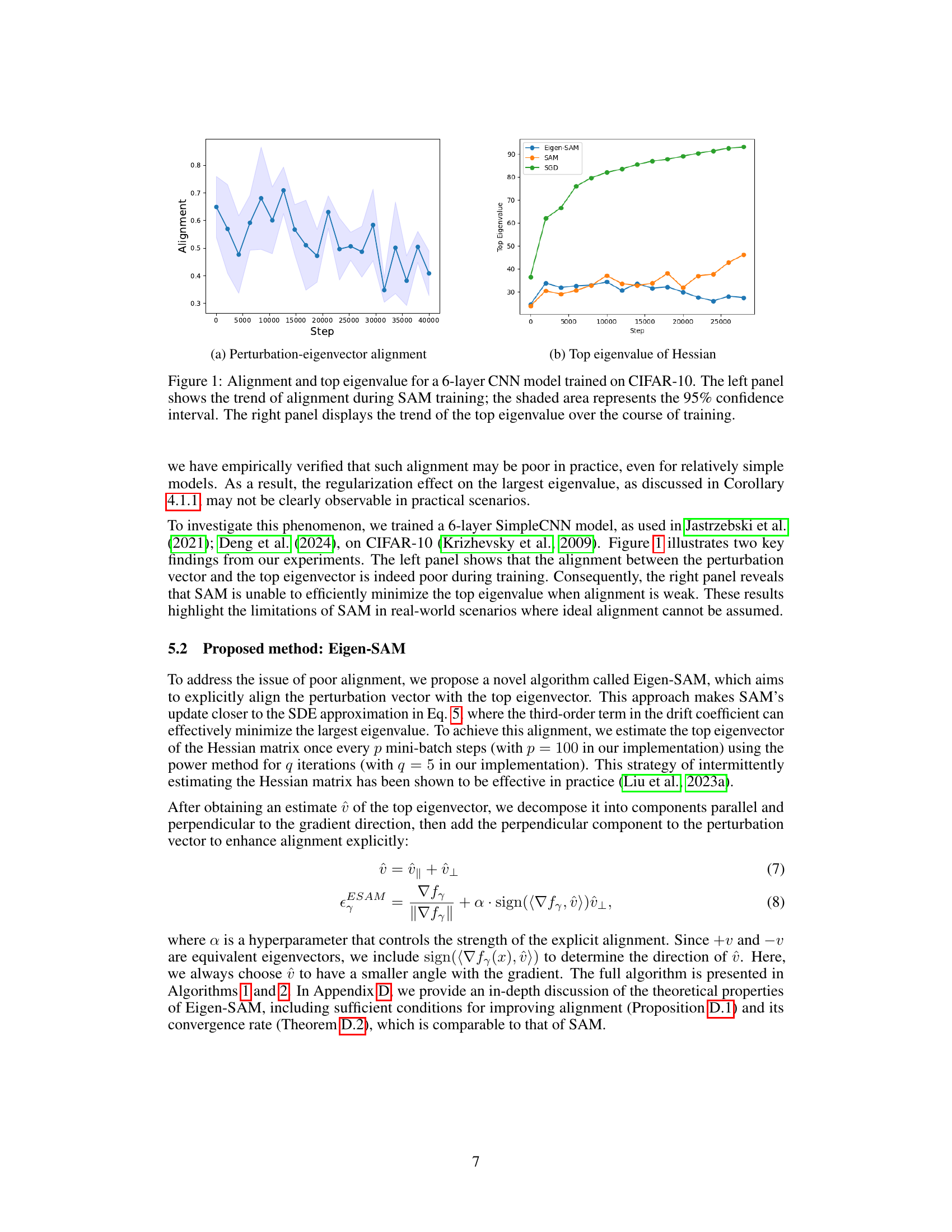
This figure consists of two sub-figures. The left sub-figure (a) shows the trend of perturbation-eigenvector alignment during the training process of SAM. The shaded area represents the 95% confidence interval. The right sub-figure (b) shows the trend of the top eigenvalue of the Hessian matrix during training for SAM, Eigen-SAM, and SGD. The figure demonstrates that the alignment between the perturbation vector and the top eigenvector of the Hessian is often poor during training, which limits the effectiveness of SAM in regularizing sharpness. Eigen-SAM shows a significantly lower top eigenvalue compared to SAM and SGD.

This table presents the test accuracy results achieved by different optimization methods (SGD, SAM, and Eigen-SAM) on four benchmark datasets: CIFAR-10, CIFAR-100, Fashion-MNIST, and SVHN. Three different network architectures (ResNet18, ResNet50, and WideResNet-28-10) were used to evaluate each method. The results are presented as mean ± standard deviation, indicating the performance variability. The table aims to demonstrate the improved generalization capability of Eigen-SAM compared to traditional SGD and SAM.

In-depth insights

#

SAM Dynamics

#

Analyzing SAM dynamics involves understanding how the Sharpness-Aware Minimization algorithm modifies the training process. SAM’s core mechanism is to perturb model parameters along the gradient’s direction before each gradient update, aiming to find flatter minima and improve generalization. The effectiveness hinges on how the perturbation interacts with the Hessian of the loss landscape. A key aspect is whether the perturbation vector aligns with the Hessian’s leading eigenvector. Ideal alignment leads to efficient sharpness reduction. However, this alignment might not hold in practice, limiting SAM’s performance. Higher-order analysis (beyond second-order approximations) is crucial to fully capture SAM’s implicit regularization. This involves considering the impact of third-order and possibly higher-order terms on the training trajectory. Such higher-order analysis is vital for a more complete understanding and potential improvements to SAM.

Eigen-SAM

#

Eigen-SAM, as a proposed algorithm, directly addresses the limitations of the standard Sharpness-Aware Minimization (SAM) method by explicitly promoting alignment between the perturbation vector and the top eigenvector of the Hessian. This crucial modification enhances SAM’s effectiveness in regularizing sharpness, a key factor impacting generalization performance in deep learning models. The core idea revolves around intermittently estimating the top eigenvector and incorporating its gradient-orthogonal component into the perturbation vector. This ensures the perturbation actively targets the direction of highest curvature, leading to a more focused and effective reduction of sharpness. Eigen-SAM’s theoretical foundation builds upon a novel third-order stochastic differential equation (SDE) analysis of SAM, revealing the complex interplay of second and third-order terms driving its dynamics, and the critical role of eigenvector alignment. Empirical evidence validates Eigen-SAM’s superiority, showcasing its consistent improvement over SAM and other related methods across various benchmark datasets and model architectures. Despite a slight increase in computational overhead due to eigenvector estimation, the significant gains in generalization accuracy demonstrate Eigen-SAM’s practical advantages and its potential for broader adoption in the field. Furthermore, Eigen-SAM offers a valuable contribution to our understanding of the implicit regularization mechanisms within SAM and provides a more robust approach for achieving improved generalization performance in deep learning.

Hessian Regularization

#

Hessian regularization techniques aim to improve the generalization performance of machine learning models by modifying the Hessian matrix of the loss function. The Hessian matrix captures the curvature of the loss landscape, and its properties are directly linked to the sharpness of minima. Sharp minima, characterized by high curvature, tend to generalize poorly, while flat minima often lead to better generalization. Hessian regularization methods work by either explicitly or implicitly altering the Hessian’s eigenvalues or eigenvectors. Explicit methods might directly modify the Hessian during optimization, for instance, by adding regularization terms that penalize large eigenvalues. Implicit methods, such as sharpness-aware minimization (SAM), indirectly influence the Hessian’s properties by focusing on the gradient and its relationship to the loss landscape. Understanding the interplay between gradient and Hessian is crucial for designing effective regularization strategies and enhancing the generalization capabilities of machine learning models. Research in this area explores the theoretical analysis of various methods, examining their effects on the loss landscape and ultimately on model generalization.

Alignment Effects

#

The concept of “Alignment Effects” in the context of a research paper likely refers to the impact of aligning specific vectors or parameters within a model or algorithm. This could manifest in various ways, such as the alignment of a perturbation vector with the top eigenvector of a Hessian matrix, as seen in sharpness-aware minimization techniques. Strong alignment often leads to improved generalization and efficiency by directly targeting the most impactful directions in the optimization landscape. Conversely, poor alignment might hinder performance and lead to suboptimal results. The paper probably explores the theoretical and empirical aspects of this alignment, potentially deriving bounds or establishing relationships between the degree of alignment and key metrics like generalization error or convergence speed. A significant part of the analysis may involve investigating the conditions under which optimal alignment is achieved or whether deliberate alignment strategies (e.g., an algorithm modification) can yield practical benefits beyond those achieved through implicit alignment alone. The significance of alignment effects is likely highlighted through experiments demonstrating the impact of alignment (or misalignment) on model performance under various conditions.

Future Work

#

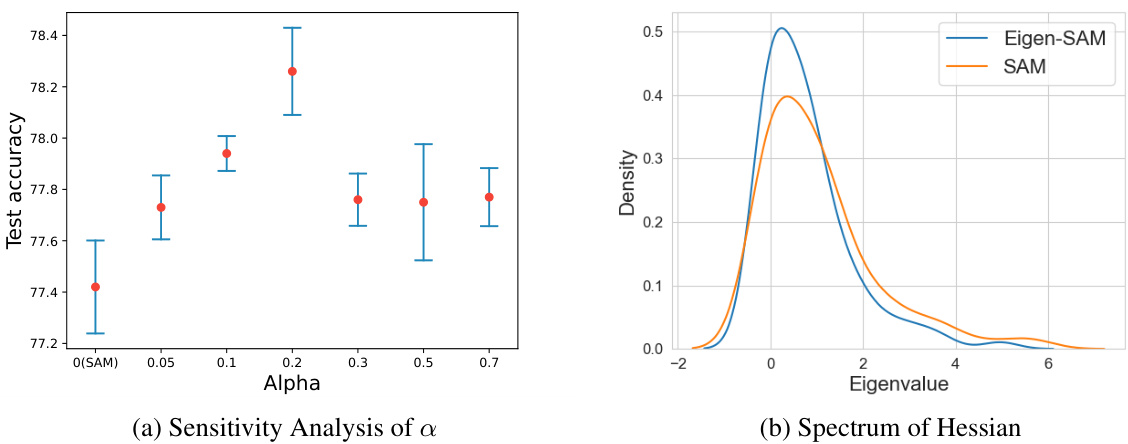
Future research directions stemming from this work could center on improving the efficiency of Eigen-SAM. The current method’s computational overhead, due to Hessian eigenvector estimation, could be reduced through the exploration of more efficient approximation techniques, such as stochastic Lanczos methods or tailored iterative procedures. Another avenue is extending the theoretical analysis beyond the current third-order SDE approximation. Investigating higher-order terms or alternative mathematical frameworks, like continuous-time optimization theory, may provide deeper insights into SAM’s implicit regularization effects. Furthermore, a crucial area for exploration would involve generalizing Eigen-SAM’s applicability to more complex tasks and broader model architectures, including exploring its interaction with various optimizers and regularization schemes beyond SGD. Finally, a comprehensive study of the impact of perturbation magnitude (p) and alignment parameter (a) on generalization performance across different network depths and datasets is needed, to provide more robust guidelines for hyperparameter tuning and ultimately achieve even greater improvements in generalization.

More visual insights

#

More on figures

This figure shows the results of training a 6-layer Convolutional Neural Network (CNN) on the CIFAR-10 dataset using three different optimization methods: Sharpness-Aware Minimization (SAM), Eigen-SAM (a proposed variant of SAM), and standard Stochastic Gradient Descent (SGD). The left panel shows the alignment between the perturbation vector used in SAM and the top eigenvector of the Hessian matrix during training. A high degree of alignment is desirable for effective sharpness reduction. The right panel shows the top eigenvalue of the Hessian matrix over the training process. A smaller top eigenvalue typically indicates better generalization. The figure demonstrates that while SAM shows some improvement over SGD, Eigen-SAM achieves better alignment and consequently reduces the top eigenvalue more effectively.

This figure compares the training dynamics of three different approaches: discrete SAM, a second-order stochastic differential equation (SDE), and the authors’ proposed third-order SDE. Six key metrics are plotted over training steps: training loss, test loss, test accuracy, parameter norm, gradient norm, and the top eigenvalue of the Hessian. The plots visually demonstrate the differences in how each method affects the loss landscape and key stability indicators during the training process.

This figure displays two sub-figures. The left sub-figure shows the trend of alignment between the perturbation vector and the top eigenvector during the training process of SAM algorithm on a 6-layer CNN model trained on CIFAR-10 dataset. The shaded area indicates the 95% confidence interval. The right sub-figure shows the trend of the top eigenvalue of the Hessian matrix over the training process. Both sub-figures show that the alignment between the perturbation vector and the top eigenvector is poor, and SAM does not effectively minimize the top eigenvalue.

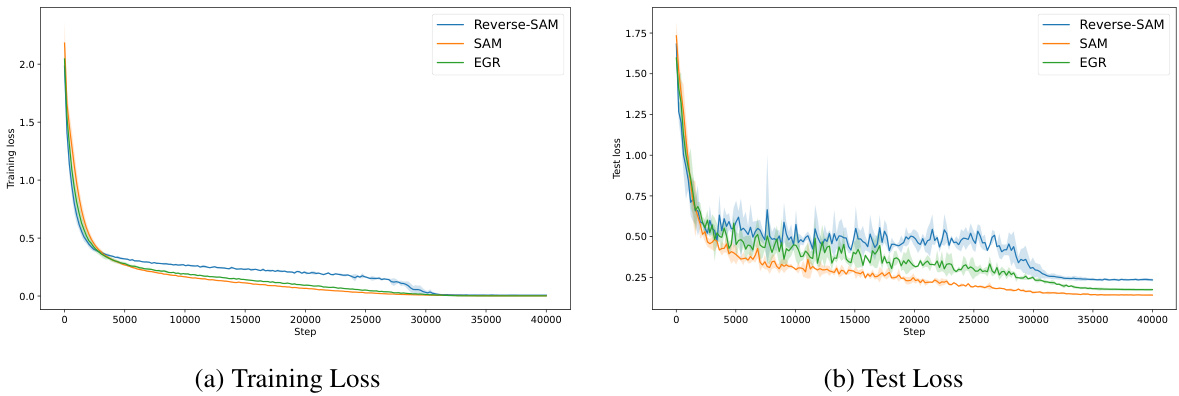
This figure compares the training and test loss curves for three different algorithms: SAM, Reverse-SAM, and EGR. The plots show the loss values over the course of training. Reverse-SAM uses the negative of the normalized gradient as the perturbation vector, while EGR explicitly regularizes the gradient norm. The goal is to demonstrate the limitations of existing theories in explaining SAM’s practical outcomes by showing that the performance of these alternative algorithms differs significantly from SAM. The figure provides empirical evidence highlighting the discrepancies between theoretical analysis and practical observations in the context of sharpness-aware minimization.

This figure shows the results of training a 6-layer CNN model on the CIFAR-10 dataset using three different optimization methods: SAM, Eigen-SAM, and SGD. The left panel shows the alignment between the perturbation vector and the top eigenvector of the Hessian matrix over training steps. The shaded area indicates the 95% confidence interval for the alignment. The right panel displays the top eigenvalue of the Hessian matrix over training steps. The plots reveal that SAM struggles to efficiently minimize the top eigenvalue because the perturbation vector and the top eigenvector of the Hessian are poorly aligned. Eigen-SAM, in contrast, is designed to address this alignment issue, leading to more efficient minimization of the top eigenvalue.

More on tables

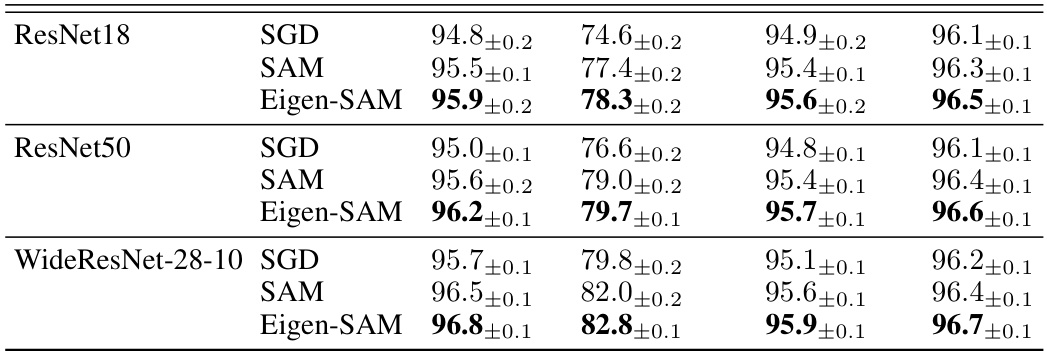
This table presents the test accuracy results achieved by three different optimization methods: SGD, SAM, and Eigen-SAM. The results are reported for four different image classification datasets: CIFAR-10, CIFAR-100, Fashion-MNIST, and SVHN. Three different network architectures were used: ResNet18, ResNet50, and WideResNet-28-10. The table shows that Eigen-SAM consistently outperforms both SGD and SAM across all datasets and architectures, demonstrating its effectiveness in improving generalization performance.

This table presents the test accuracy results for fine-tuning a Vision Transformer (ViT-B-16) model pre-trained on ImageNet-1K, specifically for the CIFAR-10 and CIFAR-100 datasets. Three optimization methods are compared: SGD (Stochastic Gradient Descent), SAM (Sharpness-Aware Minimization), and Eigen-SAM (the proposed method). The results show the test accuracy achieved by each method, along with the corresponding 95% confidence intervals, indicating the performance variability of each algorithm across different runs. The table highlights the performance improvement achieved by Eigen-SAM compared to both SGD and SAM, demonstrating its effectiveness in fine-tuning pre-trained models for improved generalization on image classification tasks.

This table presents the test accuracy results for different image classification models (ResNet18, ResNet50, WideResNet-28-10) trained on four benchmark datasets (CIFAR-10, CIFAR-100, Fashion-MNIST, SVHN) using three optimization methods: standard SGD, SAM (Sharpness-Aware Minimization), and Eigen-SAM (the proposed method). The results are presented as mean ± standard deviation, illustrating the performance comparison across various architectures and datasets.

This table presents the test accuracy results for different image classification datasets (CIFAR-10, CIFAR-100, Fashion-MNIST, and SVHN) using various models (ResNet18, ResNet50, and WideResNet-28-10) and optimization methods (SGD, SAM, and Eigen-SAM). The table shows the mean test accuracy and standard deviation for each combination, highlighting the performance improvement achieved by Eigen-SAM compared to standard SAM and SGD.

Full paper

#