↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many existing graph contrastive learning (GCL) methods struggle with the specificity, complexity, and incompleteness of their graph augmentation (GA) techniques. GAs designed for specific scenarios may not generalize well, and finding optimal augmentations can be computationally expensive. Existing learnable GAs are also limited by the finite selection of available options.
This paper addresses these challenges by proposing a novel unified GA module called UGA. UGA reinterprets GAs from a message-passing perspective, enabling the unification of node, edge, attribute, and subgraph augmentations. Based on UGA, the authors introduce GOUDA, a generalized GCL framework that incorporates widely-used contrastive losses and a novel independence loss. GOUDA achieves superior performance compared to existing GCLs, demonstrating its generality and efficiency across diverse datasets and tasks.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in graph contrastive learning because it introduces a unified and efficient graph augmentation module, addressing the limitations of existing methods. It enhances the generalizability and efficiency of graph contrastive learning models, opening avenues for broader applications and improved performance.
Visual Insights#

This figure illustrates the motivation behind unifying graph augmentations (GAs) in graph contrastive learning (GCL). It shows four types of augmentations (node, edge, attribute, and subgraph) applied to a sample graph from both spatial and message-passing perspectives. The spatial perspective highlights the global changes to the graph structure, while the message-passing perspective reveals the localized effect of these augmentations on node attributes. The key takeaway is that despite their apparent differences in the spatial domain, these augmentations all produce local attribute modifications when viewed from the message-passing perspective. This insight is crucial for developing a unified approach to GA in GCLs.
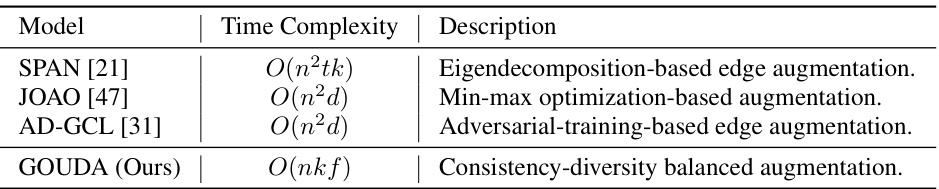
This table compares the time complexity of the augmentation phase for four different graph contrastive learning models: SPAN, JOAO, AD-GCL, and the proposed GOUDA. The time complexity is expressed in Big O notation as a function of the number of nodes (n), number of edges (m), dimension of attributes (f), and dimension of hidden layers (d). The table shows that GOUDA has a lower time complexity than the other three models, making it more efficient for large graphs.
In-depth insights#
Unified Graph Augmentation#
The concept of “Unified Graph Augmentation” proposes a significant advancement in graph contrastive learning. Instead of employing disparate augmentation strategies (node, edge, attribute, subgraph), a unified approach is suggested. This streamlines the augmentation process, potentially reducing computational complexity and improving efficiency. A key advantage lies in the generalizability of the unified method; models trained on a unified approach should transfer more readily to diverse graph tasks and structures compared to models trained with specialized augmentations. This unification could lead to more robust and versatile graph representation learning models that are less sensitive to the specifics of individual augmentation techniques and, hence, improve the overall model performance and its applicability to real-world scenarios. The core idea is to learn invariant representations, not dependent on the specific augmentation strategy. However, challenges remain. The design and implementation of such a unified module require careful consideration to ensure that it can effectively capture the essence of all other augmentation techniques without introducing new limitations or losing crucial information during the augmentation phase. The effectiveness of this unified method needs thorough empirical validation across various graph datasets and downstream tasks to solidify its true potential and impact.
Message-Passing Perspective#
The ‘Message-Passing Perspective’ offers a novel framework for understanding graph augmentations (GAs) in graph contrastive learning (GCL). Instead of viewing GAs as spatial manipulations (node dropping, edge removal, etc.), this perspective reinterprets them as local attribute modifications. This shift is crucial because it reveals the fundamental invariance GCL aims to learn: representations robust to local neighborhood perturbations. By framing GAs through the lens of message passing, the authors unify seemingly disparate techniques, laying the groundwork for a unified and generalized GA module, a significant contribution toward improving GCL’s generality and efficiency. This perspective’s power lies in its ability to bridge theoretical understanding and practical implementation, paving the way for more versatile and computationally efficient GCL models.
GOUDA Framework#
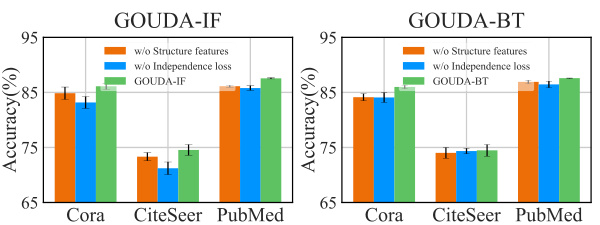
The GOUDA framework presents a novel approach to generalized contrastive learning on graphs by introducing a unified graph augmentation (UGA) module. UGA’s key innovation is its ability to reinterpret diverse graph augmentation methods from a message-passing perspective, unifying node, edge, attribute, and subgraph augmentations. This unification streamlines the augmentation process, reducing computational overhead and improving model generalization. GOUDA further enhances performance by incorporating a novel independence loss in addition to standard contrastive losses. This dual-loss function optimizes for both the consistency and diversity of augmentations, addressing limitations in existing approaches. The framework’s design promotes adaptability and efficiency, making it suitable for various graph tasks and scenarios. Evaluations demonstrate GOUDA’s superiority over existing GCLs, showcasing its potential for various real-world applications. The integration of UGA and the dual-loss function are key strengths leading to improved accuracy and efficiency. However, the paper notes some limitations, particularly regarding robustness to specific types of attacks on node attributes. Future work could address this and further explore the method’s applications.
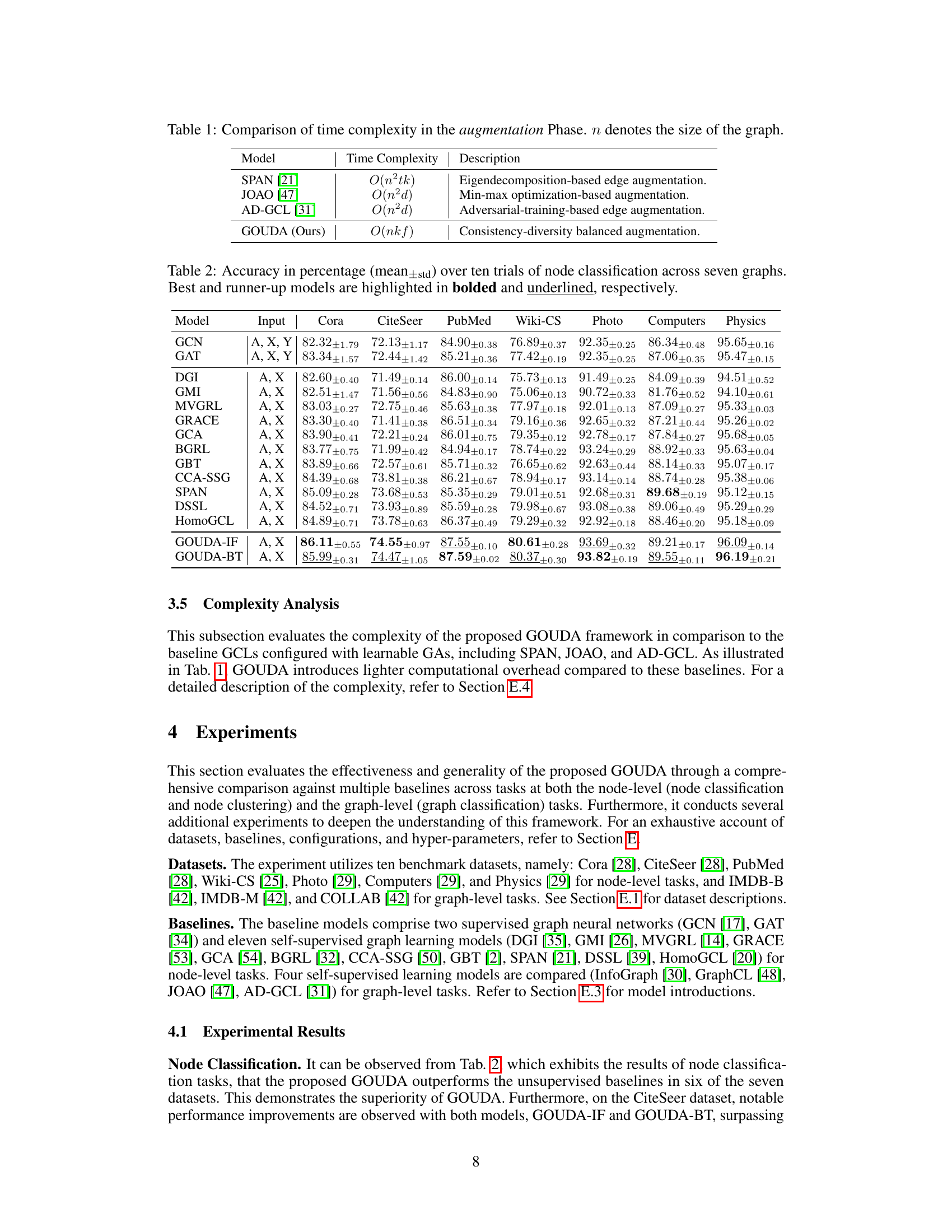
Experimental Results#
The ‘Experimental Results’ section of a research paper is crucial for demonstrating the validity and effectiveness of the proposed methods. A strong presentation will clearly articulate the metrics used, such as accuracy, precision, recall, F1-score, or AUC, depending on the task. Results should be presented across multiple datasets to showcase generalizability and robustness. Comparison with state-of-the-art baselines is essential to highlight the improvement achieved. Statistical significance testing (e.g., t-tests or ANOVA) should be applied to confirm that observed differences are not due to chance. Furthermore, it is important to discuss any unexpected or counter-intuitive results and offer potential explanations. Error bars or confidence intervals should be included to convey the uncertainty associated with the reported metrics. Finally, the discussion must go beyond a simple tabulation of numbers; it should delve into the results themselves, extracting insights and interpreting trends to contribute meaningfully to the broader research field.
Future Directions#
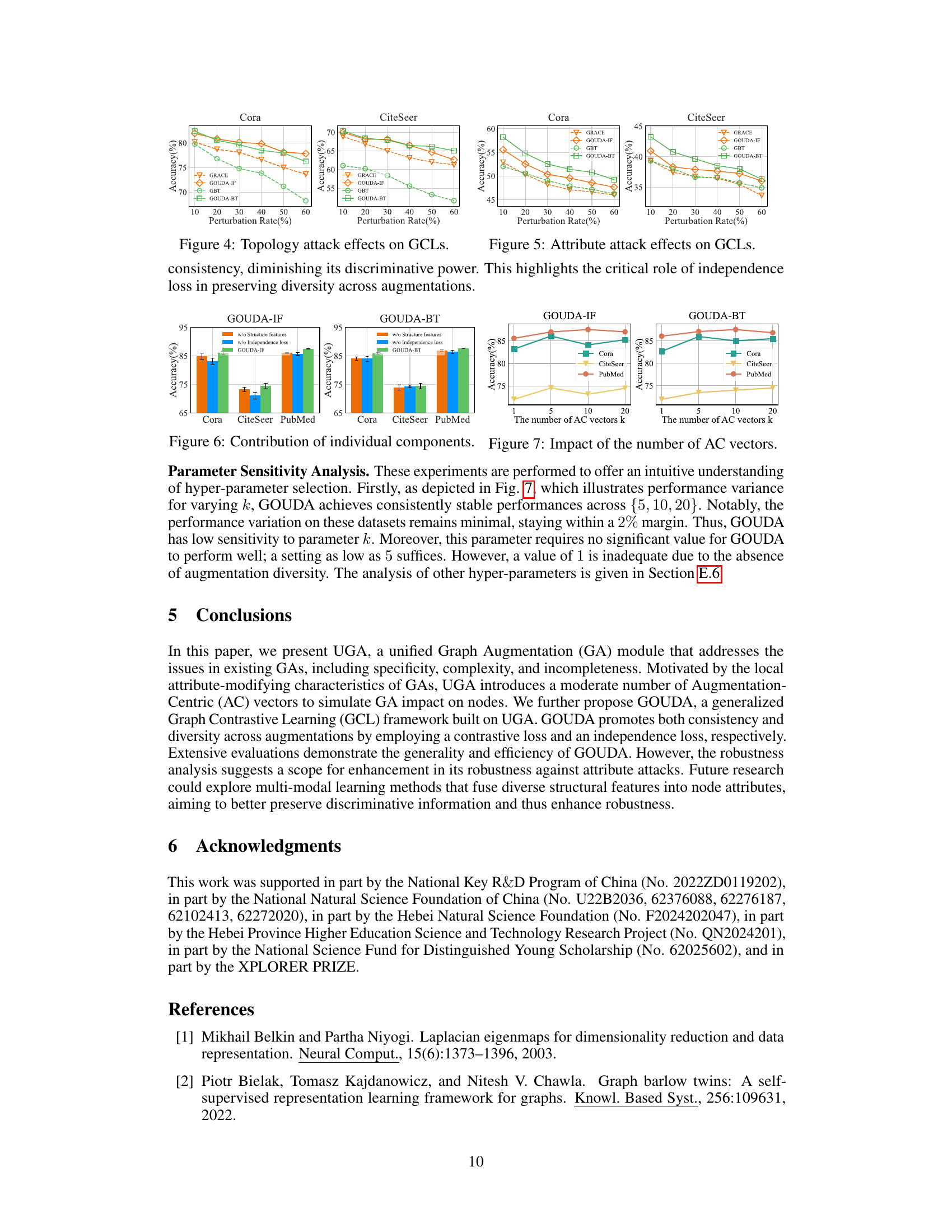
Future research could explore several promising avenues. Improving the robustness of GOUDA against attribute attacks is crucial, perhaps by incorporating more sophisticated augmentation strategies or exploring alternative loss functions. Investigating the effectiveness of UGA with other graph neural network architectures beyond GCNs and GINs could broaden its applicability. Developing more efficient implementations of UGA is also important, potentially through the use of more advanced approximation techniques. Finally, extending GOUDA to handle dynamic graphs and other types of graph data (e.g., hypergraphs, signed graphs) would significantly enhance its versatility and practical impact. Furthermore, exploring the potential benefits of combining UGA with other self-supervised learning methods could unlock additional performance gains.
More visual insights#
More on figures

This figure illustrates the proposed Unified Graph Augmentation (UGA) module and the Generalized Graph Contrastive Learning (GOUDA) framework. Panel (a) shows how UGA simulates the effect of various graph augmentations (node, edge, attribute, subgraph) by adding augmentation-centric (AC) vectors. Panel (b) shows the overall GOUDA architecture, highlighting its two-channel design with independent losses to ensure consistency and diversity across the augmentations.

This figure shows the architecture of the proposed Unified Graph Augmentation (UGA) module and the Generalized Graph Contrastive Learning (GOUDA) framework. (a) illustrates how UGA simulates various graph augmentations by aggregating Augmentation-Centric (AC) vectors that represent attribute variations within node neighborhoods. (b) depicts the GOUDA framework, highlighting its dual-channel architecture using UGA for augmentation and the inclusion of an independence loss to ensure diversity in augmentations.

This figure illustrates the proposed Unified Graph Augmentation module (UGA) and the generalized Graph Contrastive Unified Augmentations framework (GOUDA). Panel (a) shows how UGA simulates the effect of different graph augmentations (node, edge, attribute, and subgraph) by using augmentation-centric (AC) vectors to modify node attributes within their local neighborhood. Panel (b) shows the GOUDA framework, which uses two augmented views of the graph (created by UGA) and incorporates a contrastive loss to maximize mutual information between views, and an independence loss to ensure diversity between augmentations. This design aims for robustness and generalizability across different graph tasks.

This figure shows two parts: (a) illustrates how the proposed unified graph augmentation module (UGA) simulates the effect of different graph augmentations by aggregating augmentation-centric (AC) vectors. Part (b) depicts the overall generalized graph contrastive learning framework (GOUDA), highlighting the dual-channel architecture with UGA modules and the incorporation of an independence loss to maintain diversity across augmentations.
This figure illustrates the proposed Unified Graph Augmentation (UGA) module and the Generalized Graph Contrastive Learning (GOUDA) framework. Panel (a) shows how UGA uses augmentation-centric (AC) vectors to simulate the effect of different graph augmentations (node, edge, attribute, and subgraph), highlighting that these augmentations can be viewed as local attribute modifications. Panel (b) depicts the GOUDA framework, which uses UGA in a dual-channel architecture along with contrastive and independence losses to ensure both consistency and diversity in augmentations.

This figure illustrates the proposed unified graph augmentation module (UGA) and the generalized graph contrastive learning framework (GOUDA). Panel (a) shows how the UGA module uses augmentation-centric (AC) vectors to simulate the effects of various graph augmentations (node, edge, attribute, subgraph) by modifying node attributes. Panel (b) presents the GOUDA framework, which leverages two augmented graph views generated by UGA, employing both contrastive and independence loss functions to ensure the consistency and diversity of augmentations, respectively.

This figure illustrates the proposed unified graph augmentation module (UGA) and the generalized graph contrastive learning framework (GOUDA). Panel (a) shows how UGA simulates the effect of different graph augmentations by aggregating augmentation-centric (AC) vectors that represent attribute variations in node neighborhoods. Panel (b) shows the GOUDA framework, which uses two views of the graph augmented with UGA and incorporates both contrastive loss (to ensure consistency) and independence loss (to ensure diversity).

This figure shows two parts. The first part illustrates how the proposed Unified Graph Augmentation (UGA) module simulates the effect of different graph augmentations (node, edge, attribute, and subgraph augmentations) by aggregating Augmentation-Centric (AC) vectors. The second part illustrates the overall architecture of the Generalized Graph Contrastive Learning framework (GOUDA), highlighting the dual-channel architecture, the use of the UGA module to generate augmented graphs, and the incorporation of both contrastive loss and independence loss to ensure consistency and diversity in augmentation. The independence loss is specifically applied to the AC vectors.
More on tables
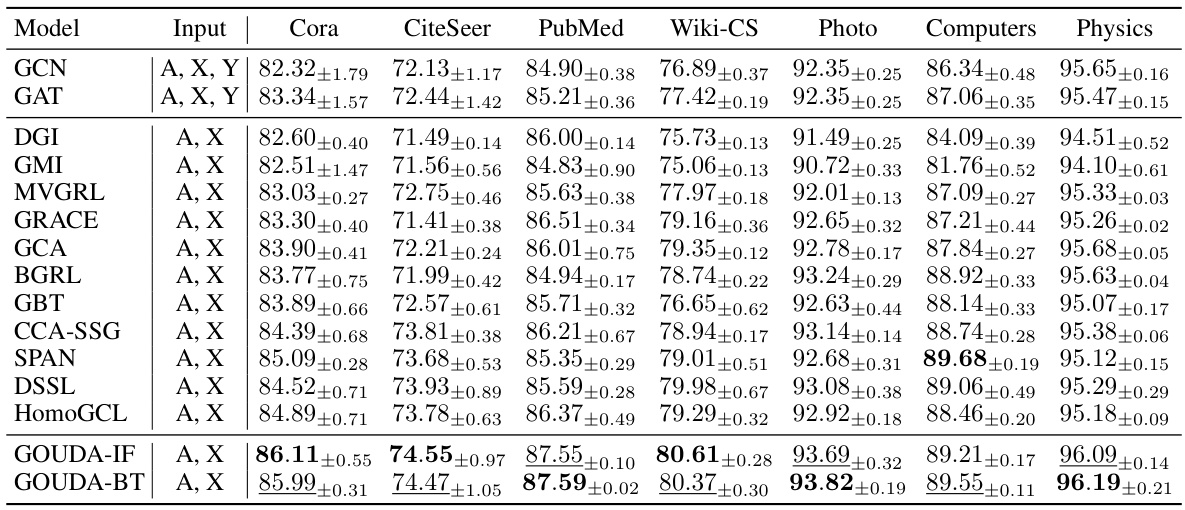
This table presents the accuracy achieved by various graph neural network models on seven benchmark datasets for node classification. The accuracy is calculated as the average of ten trials, and the standard deviation is reported. The best-performing model for each dataset is highlighted in bold, while the second-best performing model is underlined. The table allows for comparison of the performance of different models on different datasets and for identification of consistently strong performers.
This table presents the accuracy results of node classification experiments conducted on seven different graph datasets. Ten trials were performed for each dataset and the mean and standard deviation of the accuracy are reported. The best performing model and the second-best performing model for each dataset are highlighted. The results allow for comparison of the proposed GOUDA method with other state-of-the-art methods for node classification.

This table presents the results of graph classification experiments across three benchmark datasets: IMDB-B, IMDB-M, and COLLAB. The table compares the performance of the proposed GOUDA model (GOUDA-IF and GOUDA-BT) against several baseline models, including InfoGraph, GraphCL, JOAO, AD-GCL, and MVGRL. The accuracy (mean ± standard deviation) is reported for each model and dataset, providing a quantitative assessment of the proposed model’s performance relative to existing state-of-the-art methods. Higher accuracy indicates better performance.
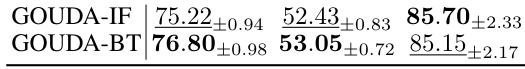
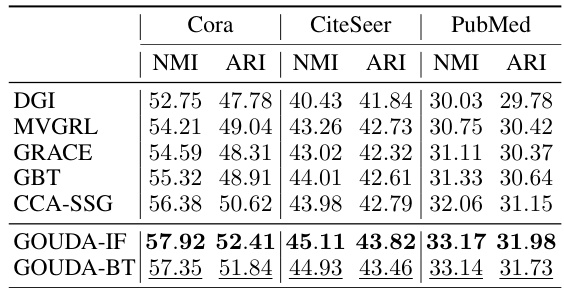
This table presents the results of node classification experiments conducted on seven different graph datasets. The accuracy (mean and standard deviation over 10 trials) is shown for various graph contrastive learning (GCL) models, including the proposed GOUDA model (GOUDA-IF and GOUDA-BT). The best-performing model for each dataset is bolded and underlined, highlighting the relative performance of GOUDA compared to existing GCL methods.
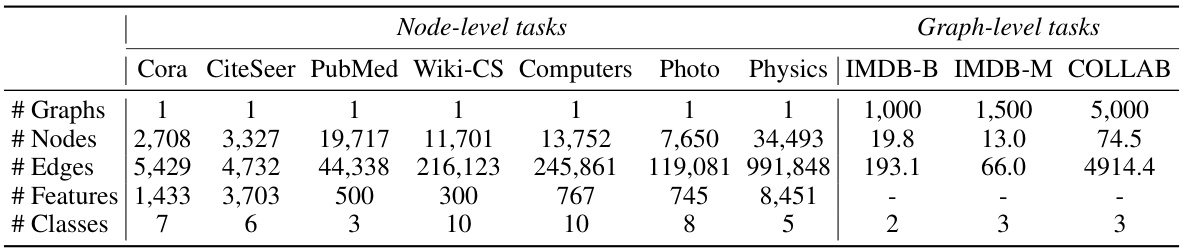
This table presents the characteristics of ten graph datasets used in the paper’s experiments. For each dataset, it lists the number of graphs, nodes, edges, features, and classes. The datasets are categorized into node-level tasks (Cora, CiteSeer, PubMed, Wiki-CS, Computers, Photo, Physics) and graph-level tasks (IMDB-B, IMDB-M, COLLAB). The information provided is essential for understanding the scale and complexity of the datasets used in the evaluation of the proposed GOUDA framework.

This table presents the results of node classification experiments conducted on seven different graph datasets. Multiple graph neural network (GNN) models, both supervised and self-supervised, were evaluated. The accuracy of each model is reported as the mean and standard deviation across ten trials. The best-performing model for each dataset is bolded and underlined, indicating which models achieved superior performance in node classification tasks.
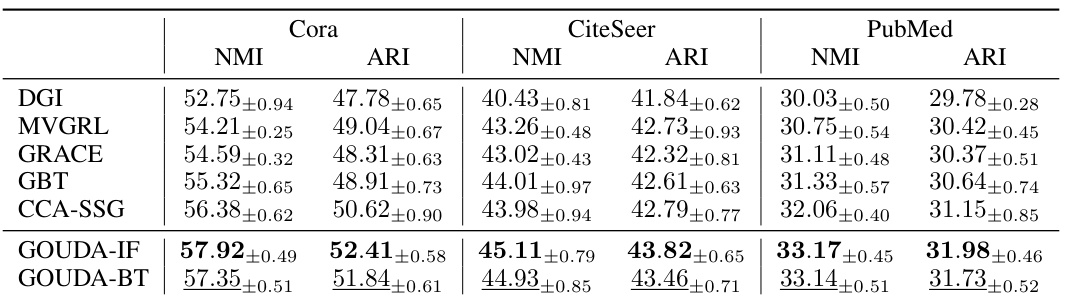
This table presents the results of node classification experiments conducted on seven different graph datasets. The accuracy of various models, including GCN, GAT, DGI, GMI, MVGRL, GRACE, GCA, BGRL, GBT, CCA-SSG, SPAN, DSSL, HomoGCL, and the proposed GOUDA, is reported, with the best and second-best results highlighted. The mean accuracy and standard deviation over ten trials are given for each model and dataset. The table offers a comprehensive comparison of the proposed GOUDA model with state-of-the-art models on a range of node classification tasks.

This table presents the results of node classification experiments conducted on seven different graph datasets. The accuracy of various graph contrastive learning (GCL) models and baseline methods (GCN, GAT, DGI, GMI, MVGRL, GRACE, GCA, BGRL, GBT, CCA-SSG, SPAN, DSSL, HomoGCL, GOUDA-IF, and GOUDA-BT) are reported. The best-performing model in each dataset is bolded, and the second-best performing model is underlined. The table provides a comparative analysis of the performance of different GCL models and highlights the superiority of the proposed GOUDA model.
Full paper#