↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Stochastic linear bandits optimize rewards by linearly weighting features, but existing approaches often assume known sparsity (number of relevant features). This limits their effectiveness in real-world situations. Moreover, existing algorithms often struggle with adversarially generated action sets, a more challenging scenario than stochastic ones.
This paper introduces SparseLinUCB, a novel algorithm addressing these issues. It cleverly uses a randomized model selection method across a hierarchy of confidence sets to achieve state-of-the-art sparse regret bounds even without knowing the sparsity or facing adversarial action sets. A variant, AdaLinUCB, further enhances empirical performance in stochastic linear bandits.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on sparse linear bandits, a vital area in online learning and decision-making. It presents novel algorithms that achieve state-of-the-art performance without relying on prior knowledge of sparsity or restrictive assumptions on action sets. This addresses a major limitation in existing methods and opens new avenues for improving efficiency and adapting to real-world scenarios characterized by unknown sparsity and adversarial actions.
Visual Insights#
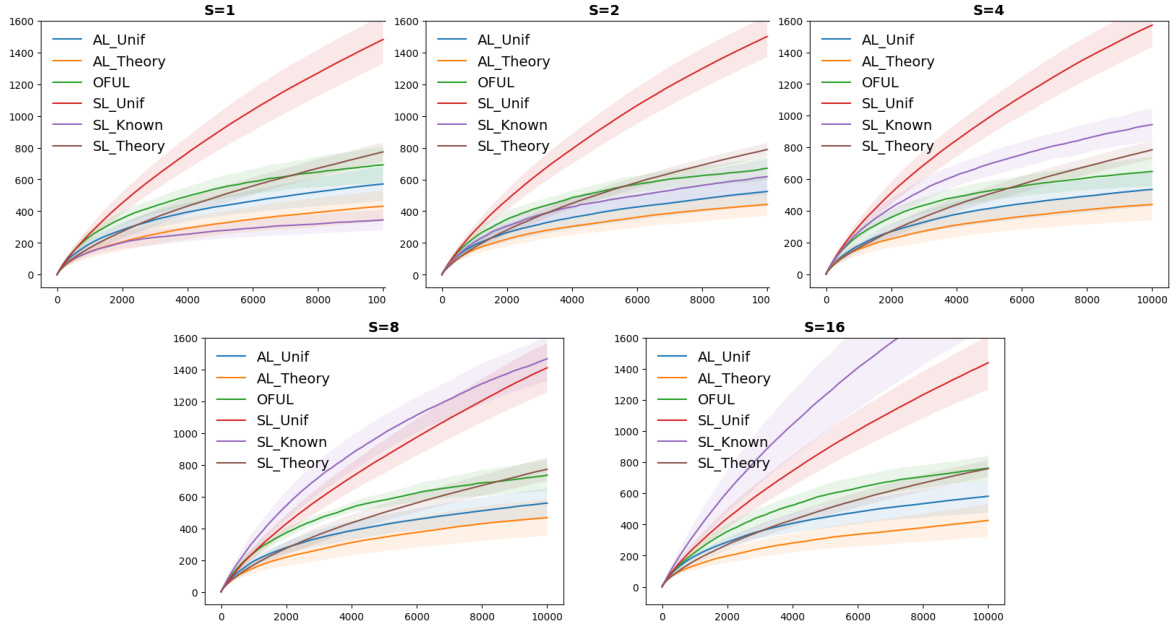
This figure shows the experimental results comparing the performance of AdaLinUCB and SparseLinUCB with OFUL under different sparsity levels (S = 1, 2, 4, 8, 16). Each plot displays cumulative regret against the time steps. The shaded area represents the one standard deviation bound across 20 repetitions for each algorithm. AdaLinUCB consistently outperforms OFUL and SparseLinUCB across all sparsity levels.
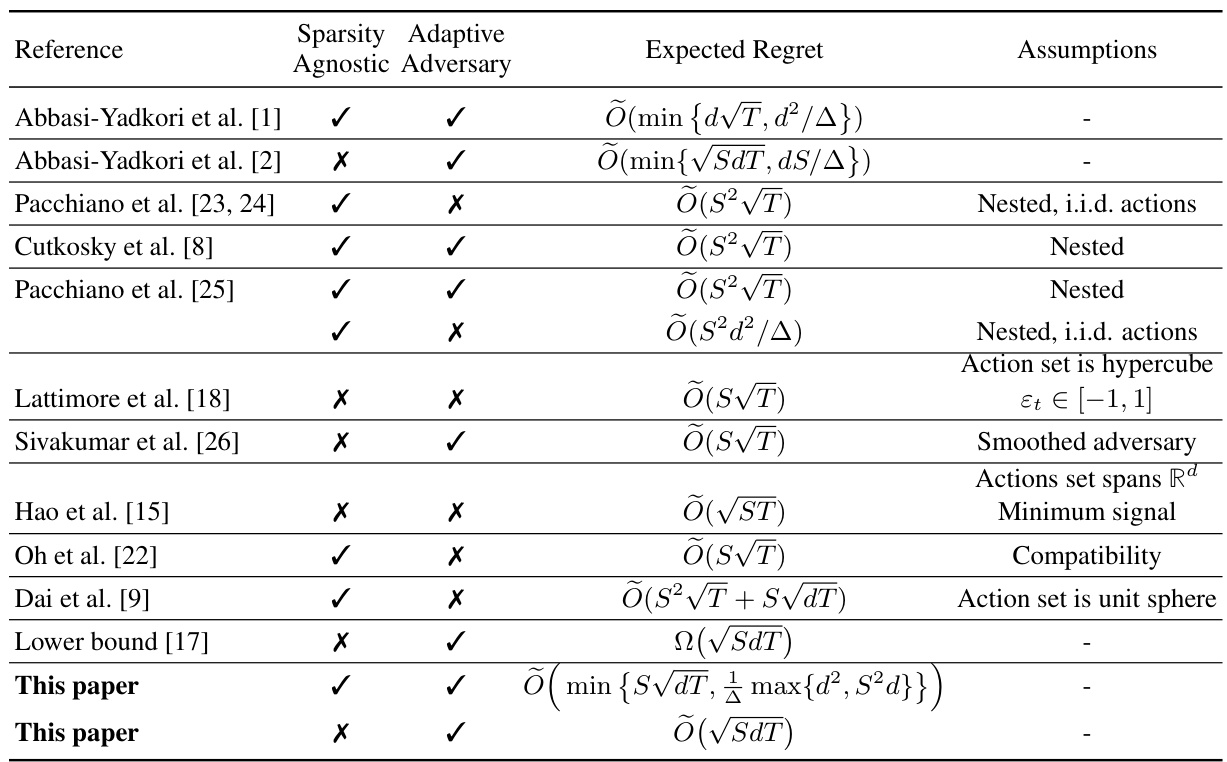
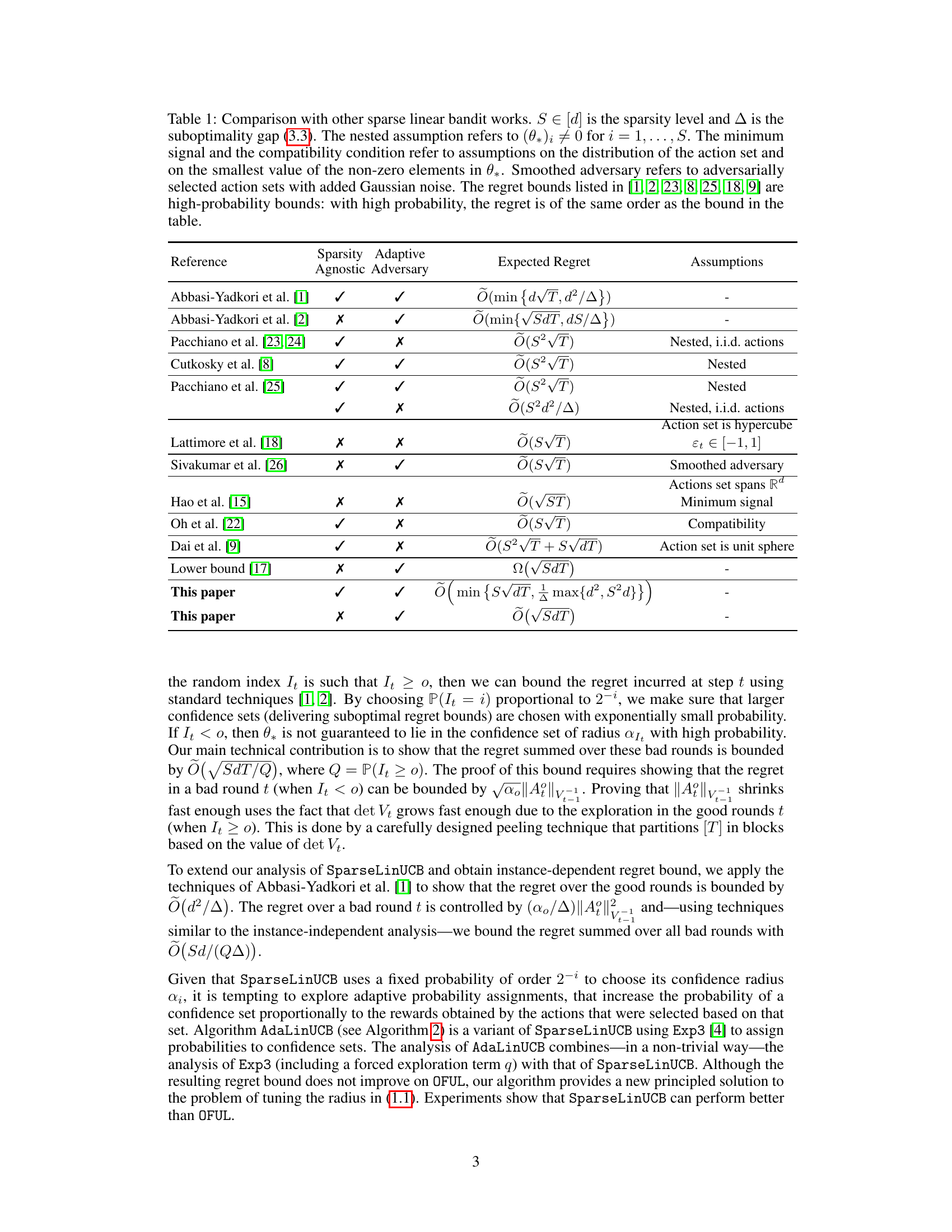
This table compares the proposed algorithm with existing sparse linear bandit algorithms. It shows the expected regret bounds achieved by each algorithm under different assumptions regarding the sparsity level, adaptive adversary, and action set properties. The table highlights the novelty of the proposed algorithm in achieving sparse regret bounds without requiring prior knowledge of sparsity or making strong assumptions on the action sets.
Full paper#