Hamiltonian Score Matching and Generative Flows

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it bridges Hamiltonian mechanics with generative modeling, opening exciting new avenues for research. It introduces novel score matching methods and generative models, potentially improving the quality and efficiency of generative AI applications. The findings also offer new insights into diffusion models and flow-based methods, impacting various machine learning fields.

Visual Insights

#

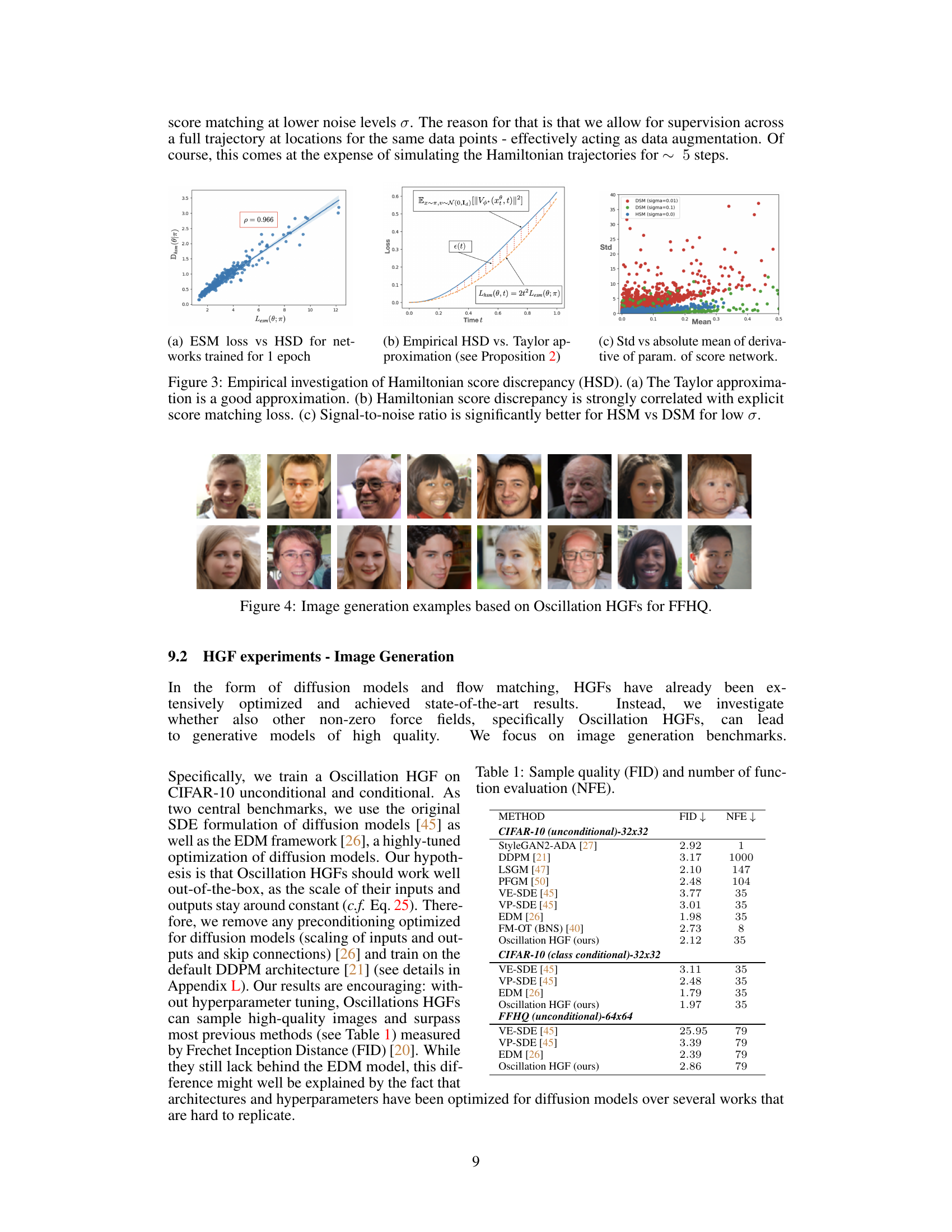
This figure shows the results of applying the Hamiltonian Score Matching (HSM) method to a Gaussian mixture dataset. Panel (a) displays the true density of the data distribution. Panel (b) shows the learned score function, which is a vector field representing the gradient of the log-density. As expected, the learned score function accurately captures the gradients of the true density. Panel (c) shows the learned velocity predictor, which ideally should be zero everywhere according to theory. The near-zero values in this panel demonstrate the effectiveness of the HSM method.

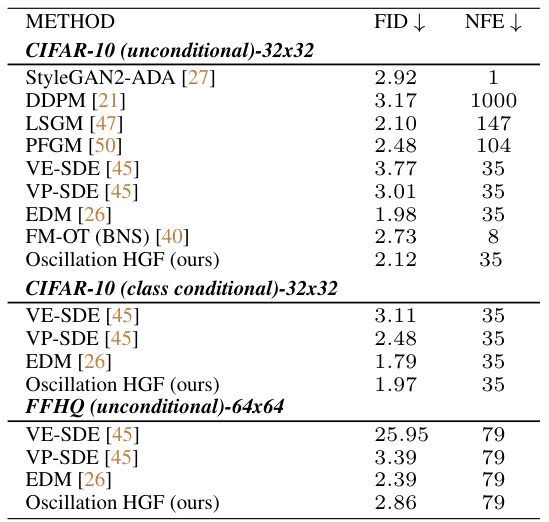
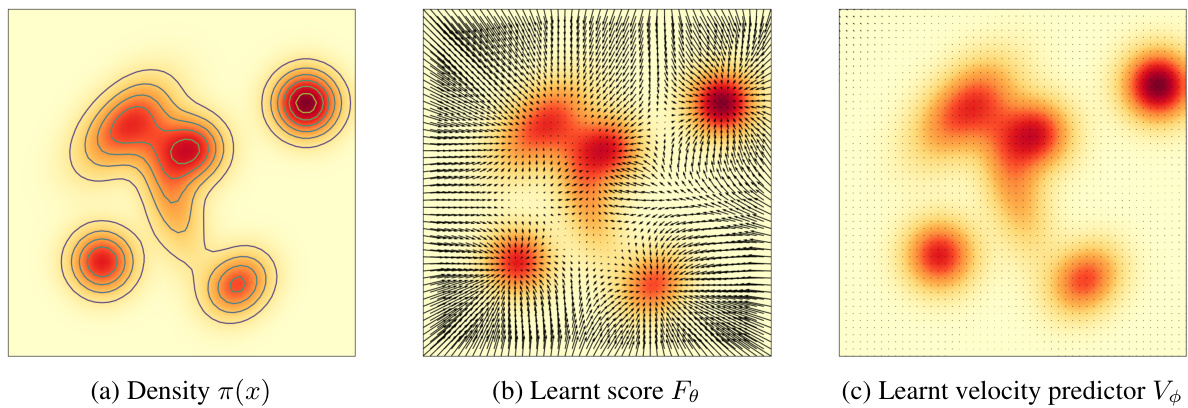
This table presents a comparison of the performance of various generative models on three image generation benchmarks: CIFAR-10 (unconditional), CIFAR-10 (class conditional), and FFHQ. The metrics used for comparison are the Fréchet Inception Distance (FID), a measure of sample quality, and the number of function evaluations (NFE), which reflects computational cost. The results show that the proposed Oscillation HGF model achieves competitive performance compared to state-of-the-art methods.

In-depth insights

#

HVP Score Matching

#

Hamiltonian Velocity Predictors (HVPs) represent a novel approach to score matching, leveraging the power of Hamiltonian dynamics. HVP score matching cleverly circumvents the limitations of traditional methods by directly estimating the velocity from the Hamiltonian ODE, without needing explicit knowledge of the score function. This avoids issues like high variance and computational cost associated with existing techniques. The core idea is to learn a velocity predictor network that, when integrated with a parameterized Hamiltonian ODE, accurately predicts the velocity given a location in data space. The proposed Hamiltonian Score Discrepancy (HSD) metric quantifies the difference between the learned velocity predictor and the true velocity, serving as an effective loss function during training. The use of HVPs is innovative and potentially more efficient, because it bypasses the explicit calculation of the score, leading to a more straightforward training process and potentially broader applicability to a wider range of generative modeling tasks. Ultimately, HVP Score Matching offers a significant advancement in score matching techniques, providing a fresh perspective and superior performance on complex datasets.

HGF Generative Flows

#

Hamiltonian Generative Flows (HGFs) represent a novel generative modeling framework that leverages Hamiltonian dynamics. HGFs unify existing methods like diffusion models and flow matching by parameterizing the Hamiltonian ODE’s force field and marginalizing out the velocity. This approach offers a flexible and expressive design space. A key contribution is the Hamiltonian Velocity Predictor (HVP), enabling efficient score function estimation and sample generation. The theoretical foundation highlights how a zero force field in HGFs recovers diffusion models, while specific force fields (e.g., harmonic oscillators in Oscillation HGFs) yield unique generative properties. This framework provides a new perspective for generative modeling and is particularly promising for integrating physical systems and dynamics into the generative process.

Oscillation HGFs

#

The proposed Oscillation HGFs represent a novel generative model stemming from the Hamiltonian Generative Flows (HGFs) framework. Instead of relying on zero force fields like diffusion models or employing learned force fields as in other HGF variants, Oscillation HGFs leverage a harmonic oscillator-inspired force field. This specific choice is motivated by its inherent scale-invariance, meaning the model’s behavior is consistent across different scales. The authors’ experiments reveal that this scale-invariance translates to improved performance, rivaling leading generative models without requiring extensive hyperparameter tuning. The simplicity and effectiveness of the Oscillation HGFs highlight the potential of deliberately designing force fields within the HGFs framework to achieve better generative modeling results. This approach also suggests a new avenue for future research: exploring other physically-inspired force fields to further enhance the performance and capabilities of generative models.

HSM Experimental

#

Hypothetical ‘HSM Experimental’ section would likely detail empirical evaluations of the Hamiltonian Score Matching (HSM) method. It would present results demonstrating HSM’s performance in score matching tasks, comparing it against existing methods like denoising score matching (DSM). Key aspects would include the datasets used (likely Gaussian mixtures initially, progressing to more complex datasets), metrics employed (e.g., Hamiltonian Score Discrepancy, explicit score matching loss), and an analysis of HSM’s variance characteristics. A core focus would be validating the theoretical claims made about HSM’s ability to provide accurate score estimations with lower variance, especially when compared to DSM at lower noise levels. The experiments might involve analyzing the impact of hyperparameters (e.g., training time, trajectory length) on HSM’s performance. Visualizations, such as plots showcasing the correlation between HSM loss and existing metrics, or comparisons of learned score fields with ground truth, would be crucial. The discussion would critically evaluate the advantages and limitations of HSM, potentially highlighting its suitability for specific applications and its computational costs.

Future Directions

#

Future research should explore more sophisticated force fields within the Hamiltonian Generative Flows (HGFs) framework, potentially incorporating knowledge from physics or other domains. Investigating alternative optimization strategies beyond the current min-max approach for Hamiltonian Score Matching (HSM) is crucial for improved efficiency and scalability. A particularly promising avenue is to explore denoising Hamiltonian score matching, leveraging the strengths of both HSM and denoising score matching. Additionally, adapting HGFs to manifold-valued data is key to expanding its applicability to scenarios such as molecular dynamics or other applications involving complex data structures. Finally, a deeper investigation into the theoretical underpinnings of HGFs, particularly exploring the connection between different classes of force fields and the resulting generative properties, would yield valuable insights for model design and interpretation.

More visual insights

#

More on figures

This figure compares three different types of Hamiltonian Generative Flows (HGFs) in a joint coordinate-velocity space. It shows how the distribution evolves over time from t=0 (blue) to t=T (red) using trajectories (black). The data distribution is a mixture of two Gaussians. It demonstrates the differences in how Diffusion models, Flow matching, and Oscillation HGFs change the distribution’s shape and location in phase space, highlighting the effect of different force fields on the distribution.

This figure empirically validates the Hamiltonian Score Discrepancy (HSD) proposed in the paper. Panel (a) shows a strong correlation between the HSD and the explicit score matching loss, confirming HSD’s effectiveness as a score matching metric. Panel (b) demonstrates the accuracy of the Taylor approximation used to connect HSD and the explicit score matching loss. Finally, panel (c) highlights the superior signal-to-noise ratio achieved by the HSM method (Hamiltonian Score Matching) compared to DSM (Denoising Score Matching) at lower noise levels, indicating HSM’s ability to generate more accurate score estimates.

This figure shows several example images generated by the Oscillation HGF model trained on the FFHQ dataset. The images demonstrate the model’s ability to generate high-quality, realistic-looking faces.

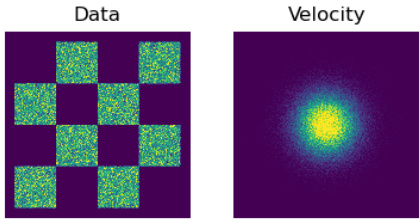
This figure shows the initial data and velocity distributions used for training Reflection HGFs. The data distribution is a checkerboard pattern, representing a mixture of data points in different regions. The velocity distribution is a central Gaussian, indicating that the initial velocities of the particles are randomly drawn from a normal distribution centered around zero. The ‘infinite force’ at the boundaries means particles bounce off the borders. This model can generate a uniform distribution without explicit ODE simulation, highlighting the flexibility of HGFs.

This figure compares the evolution of three different Hamiltonian Generative Flow (HGF) models in a joint coordinate-velocity space. The models are: diffusion models, flow matching, and oscillation HGFs. Each model starts from the same data distribution and is visualized using different colors and trajectories. The figure illustrates how the distribution evolves over time (from t=0 to t=T) in each model, highlighting the difference in their dynamics and convergence properties.

Full paper

#