↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Simulating rigid body dynamics is crucial for robotics and computer graphics, but existing methods struggle with the interplay between continuous motion and sudden changes caused by collisions. These methods also often ignore the complex, hierarchical structure of many physical systems. This leads to inaccurate and inefficient simulations.
This paper introduces EGODE, a new framework that addresses these issues. EGODE uses a coupled graph ODE to model continuous dynamics across hierarchical structures (mesh nodes and objects). It also incorporates an event module to detect and respond to collisions in real-time. Extensive experiments demonstrate that EGODE outperforms other state-of-the-art methods in accuracy and efficiency. This work is significant for its novel approach and significant improvements in rigid body dynamics modeling.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel framework for modeling rigid dynamics, a crucial aspect in various fields like robotics and computer graphics. Its innovative approach of combining graph ODEs and an event module addresses limitations of existing methods, improving the accuracy and efficiency of simulations. This opens up new avenues for developing more realistic and computationally efficient physics simulators, which is a significant trend in current research.
Visual Insights#

This figure displays a comparison of the prediction results of four different models (Ground Truth, EGODE, SGNN, EGNN) on the Physion dataset. Each model’s predictions are shown in a sequence of images representing the evolution of the physical system over time. The figure visually demonstrates the superior accuracy of EGODE in predicting the trajectories of the objects across diverse and complex scenarios, as compared to the other three models.
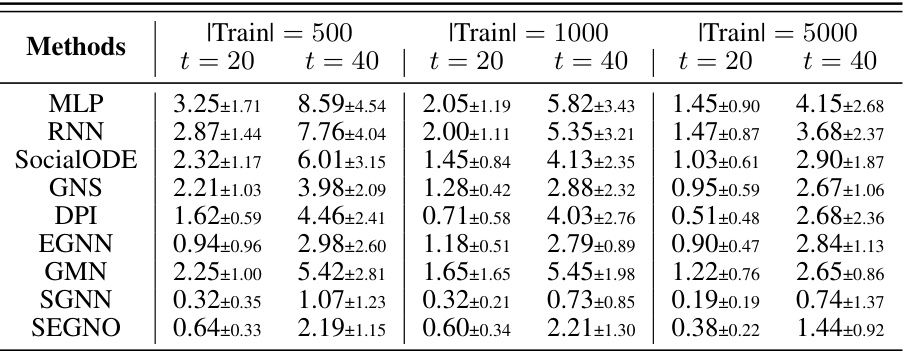
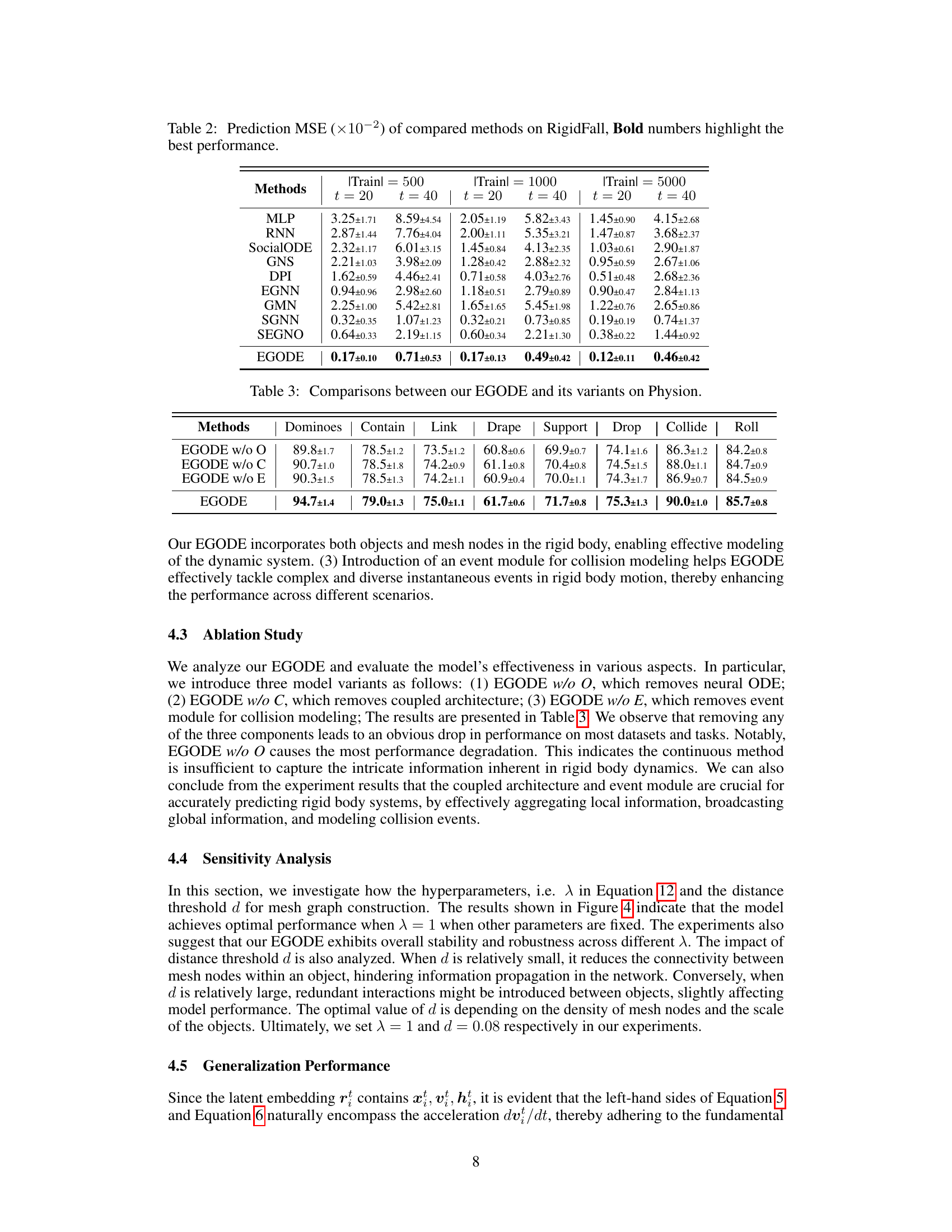
This table presents a comparison of the Mean Squared Error (MSE) achieved by various methods on the RigidFall dataset. The MSE is a measure of the difference between the predicted and actual values, indicating the accuracy of the model’s predictions. Different training set sizes (500, 1000, and 5000) are considered, and the MSE is reported for prediction horizons of 20 and 40 time steps. Bold numbers highlight the best performing method for each condition.
In-depth insights#
EGODE Framework#
The EGODE framework presents a novel approach to rigid body dynamics simulation by integrating graph neural ordinary differential equations (Graph ODEs) with an event-handling module. This dual approach addresses limitations of existing methods that struggle to effectively reconcile continuous dynamics with the instantaneous changes caused by collisions. The use of Graph ODEs enables the modeling of continuous evolution across hierarchical structures (mesh nodes and objects), while the event module specifically targets and handles collisions, improving accuracy. A key strength is the framework’s ability to jointly model both continuous and instantaneous changes, offering more realistic and accurate simulations. The hierarchical modeling, particularly the combined mesh node and object representations, allows for greater expressiveness and detail in representing complex systems. Further investigation is needed to fully assess its scalability and computational cost for extremely large systems, as well as the robustness and generalization capacity across a wider variety of scenarios beyond those presented in the paper. The source code availability enhances reproducibility and allows for community contributions and extensions, which will help drive its adoption and improve upon the model in the future.
Graph ODE Model#
A Graph ODE model leverages the strengths of both Graph Neural Networks (GNNs) and Neural Ordinary Differential Equations (NODEs) for modeling dynamic systems. GNNs excel at capturing relationships within complex, interconnected structures, represented as graphs, making them ideal for representing interactions between multiple objects. NODEs provide a framework for modeling continuous evolution, offering a more natural and accurate way to capture temporal changes compared to discrete time-step methods. By combining these, a Graph ODE model can efficiently and effectively simulate the continuous evolution of systems with complex interactions, handling both the continuous dynamics and any instantaneous changes resulting from events like collisions. This hybrid approach provides a powerful tool for various applications, including robotics, physics simulations, and other domains characterized by interconnected components exhibiting continuous change.
Collision Handling#
Effective collision handling is crucial for realistic rigid body dynamics simulation. A robust approach needs to accurately detect collisions in real-time, estimate the impact forces, and update the system’s state accordingly. This often involves sophisticated algorithms for handling complex shapes and multiple simultaneous collisions. The method should not just stop at detecting collisions but must also determine how the collision affects the objects’ velocities and angular momentum. Energy conservation and impulse calculations are key factors in maintaining physical accuracy. Different methods exist, each with trade-offs in computational cost and accuracy. Simple methods such as bounding box checks are computationally cheap but less precise, while sophisticated methods using complex geometry analysis may provide superior accuracy but demand greater processing power. Hierarchical structures, handling multiple objects, and integrating with ODE solvers are also important considerations. The choice of approach depends on factors like the complexity of the simulated environment, desired accuracy, and available computational resources.
Ablation Study#
An ablation study systematically evaluates the contribution of individual components within a machine learning model. In the context of a rigid body dynamics model, an ablation study would likely assess the impact of removing different modules (e.g., the coupled graph ODE, the event module). By removing one component at a time and measuring the resulting performance changes, researchers can pinpoint which parts are crucial for the model’s success and which are less important. This analysis helps understand the model’s strengths and weaknesses and informs future improvements by identifying areas for further development or simplification. The results from an ablation study often highlight the importance of particular components in capturing specific aspects of the dynamics, like continuous evolution versus instantaneous changes during collisions. The results could confirm that the coupled graph ODE accurately models the continuous behavior, and that the event module is essential for addressing instantaneous interactions and collisions. Ultimately, a thorough ablation study provides valuable insights into the model’s architecture and its effectiveness in solving complex physics problems.
Future of EGODE#
The future of EGODE hinges on addressing its current limitations and exploring new avenues of application. Extending EGODE to handle deformable objects and complex articulated systems is crucial for broader real-world applicability. This would involve incorporating more sophisticated physics models and potentially incorporating techniques from soft-body dynamics simulation. Improving the efficiency and scalability of the EGODE framework is essential, particularly when dealing with large-scale systems. This could entail exploring more efficient neural ODE solvers or architectural optimizations. Further research into handling uncertainty and noise in real-world data will be critical for robust performance in practical scenarios. Integrating uncertainty estimation and techniques like Bayesian methods would greatly enhance the robustness. Finally, exploring diverse applications beyond rigid body dynamics is a promising area. EGODE’s underlying graph-based framework lends itself well to other domains, including fluid dynamics, granular materials, and potentially even complex biological systems, offering significant potential for interdisciplinary research.
More visual insights#
More on figures
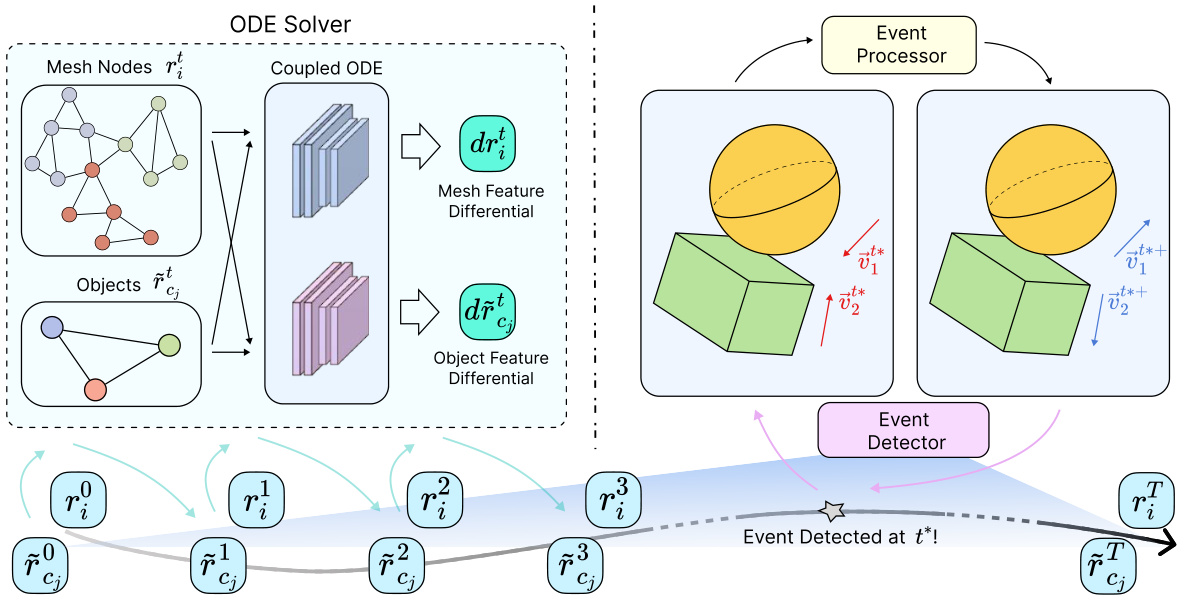
This figure provides a visual overview of the EGODE framework. It shows the coupled graph ODE framework, which models the continuous evolution of mesh nodes and objects using their features and interactions. A key component is the event module, which detects collisions and updates the system state accordingly. The figure illustrates how the framework handles both continuous dynamics and instantaneous changes caused by collisions.
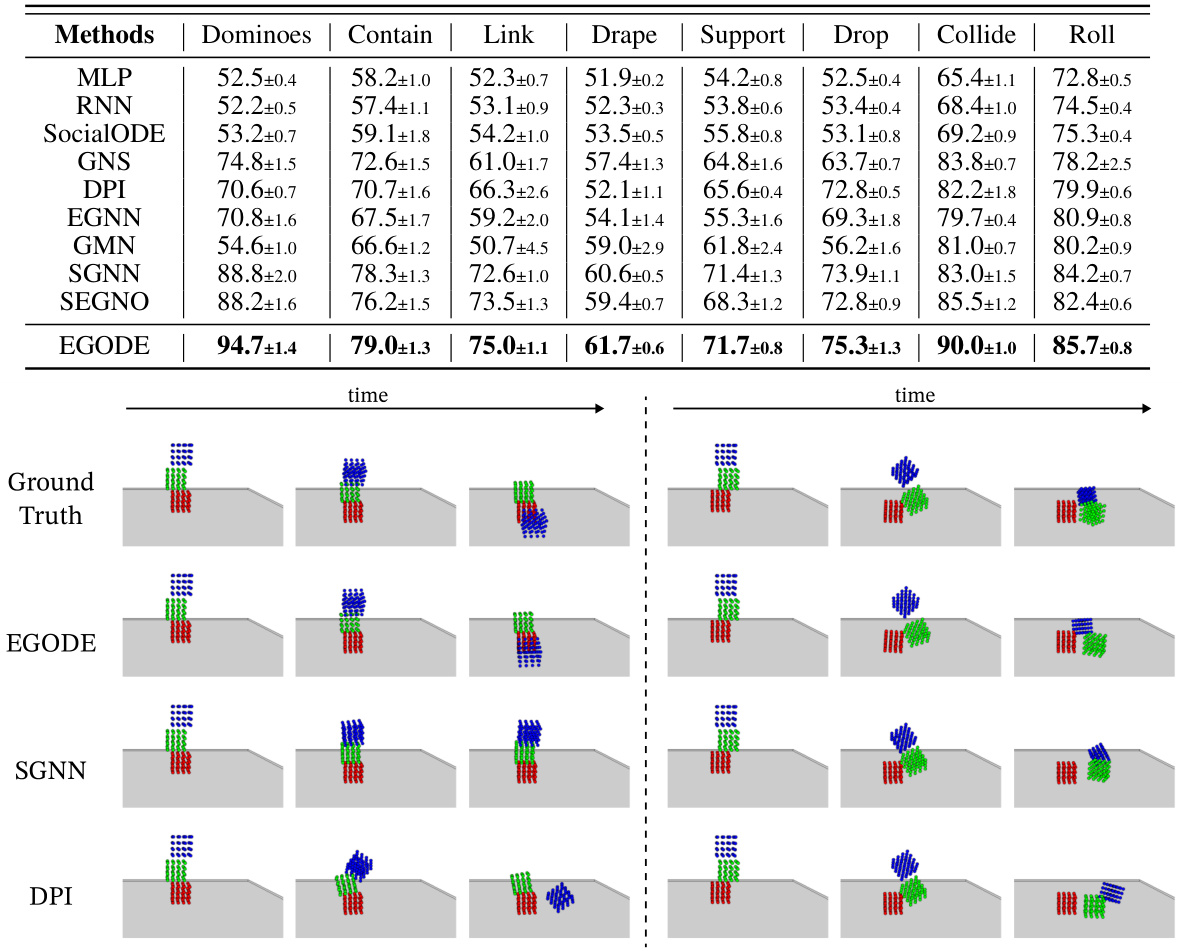
This figure shows a comparison of the ground truth and predictions generated by EGODE, SGNN, and DPI on the RigidFall dataset. The RigidFall dataset simulates collisions and interactions between three rigid cubes during falling under a varying gravitational acceleration. The figure visually demonstrates that EGODE produces significantly more accurate trajectory predictions than the other two methods (SGNN and DPI). The results showcase EGODE’s ability to generate accurate trajectories for rigid body dynamics, which is a key contribution of the paper.
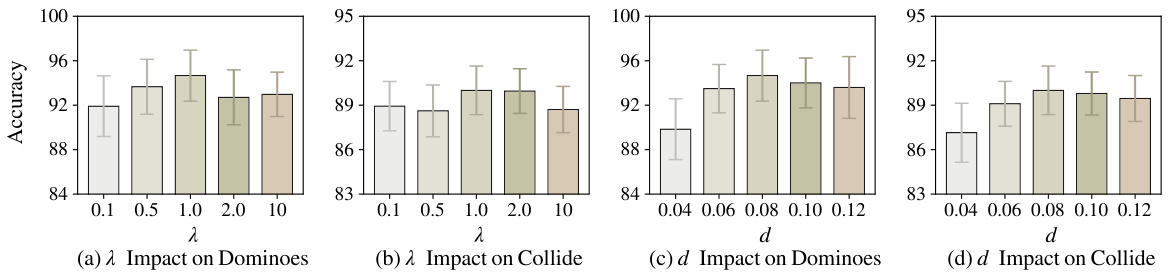
This figure shows the sensitivity analysis of the EGODE model’s performance on the Dominoes and Collide tasks from the Physion dataset with respect to two hyperparameters: λ (lambda) and d. The left two subfigures show the impact of λ on the accuracy of the model for both Dominoes and Collide tasks. The right two subfigures show the impact of d on the accuracy of the model for both Dominoes and Collide tasks. Each subfigure contains a bar chart showing the average accuracy and error bars representing the 80% confidence intervals. This analysis helps determine the optimal values for these hyperparameters to maximize the model’s performance.
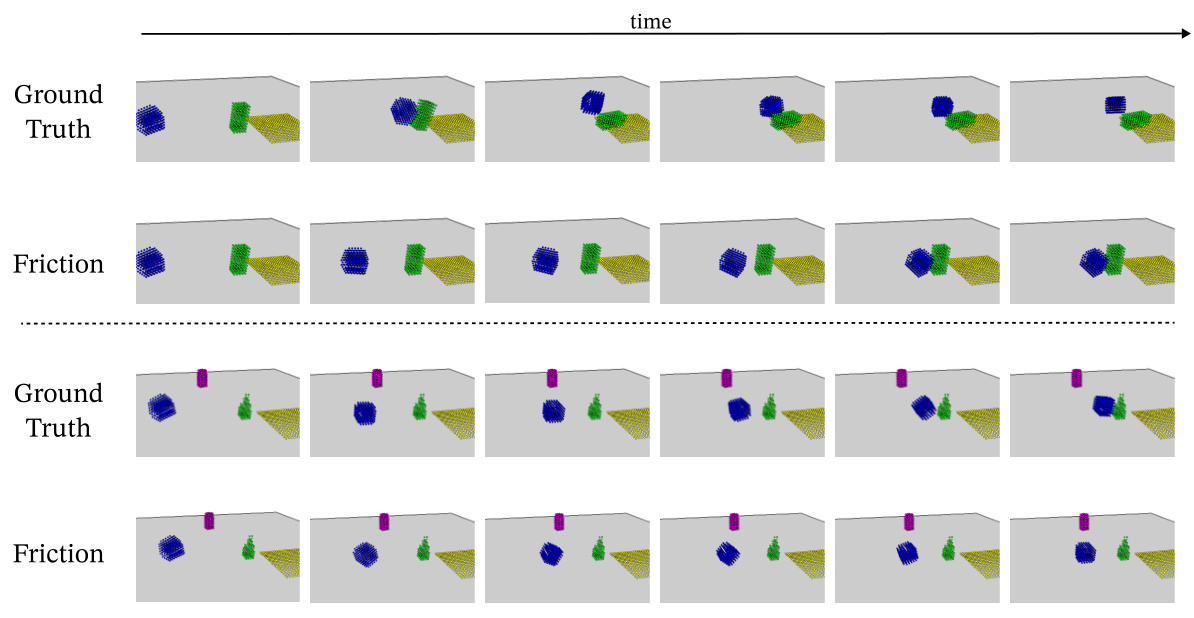
This figure compares the simulation results of EGODE with and without considering friction, against the ground truth. The top two rows show a scenario where three cubes fall and collide. The ground truth shows the expected motion. The EGODE simulation without friction shows a similar trajectory, while the simulation with friction demonstrates the effect of the added resistive force, resulting in a more realistic depiction of cube motion. The bottom two rows demonstrate a similar scenario. The difference highlights the ability of EGODE to accurately model the impact of external forces on the system’s dynamics.
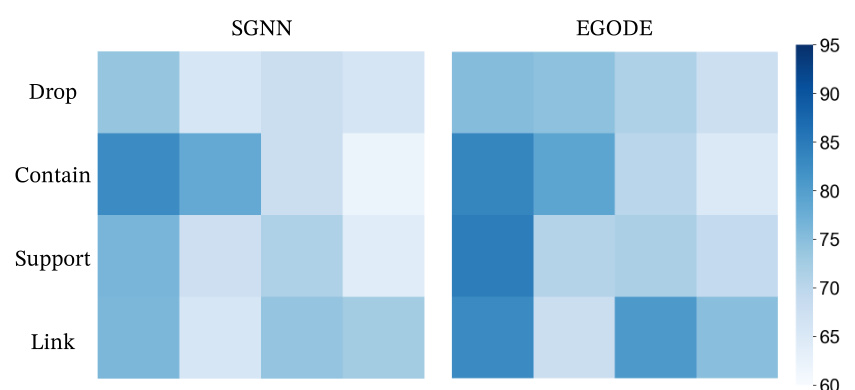
This figure displays a heatmap visualizing the generalization capabilities of two models, SGNN and EGODE, on different tasks of the Physion dataset. Each cell represents the accuracy of the model on a particular task (rows) trained on another task (columns). The color intensity represents the accuracy, with darker shades indicating higher accuracy. This helps demonstrate how well each model generalizes its learned knowledge from one task to another. The figure clearly shows EGODE’s superior generalization performance across various tasks compared to SGNN.

This figure displays a comparison of the results of three different methods (Ground Truth, EGODE, SGNN) for predicting the trajectories of objects in the Physion dataset. Each row represents a different scenario from the dataset, and the columns represent the different methods. The images show that the EGODE model produces predictions that are visually very similar to the ground truth, whereas the SGNN method produces predictions that are more noticeably different from the ground truth. The visualization demonstrates the superiority of the EGODE model in accurately predicting the trajectories of objects in complex physical simulations. The differences are particularly visible in the more challenging scenarios.
More on tables

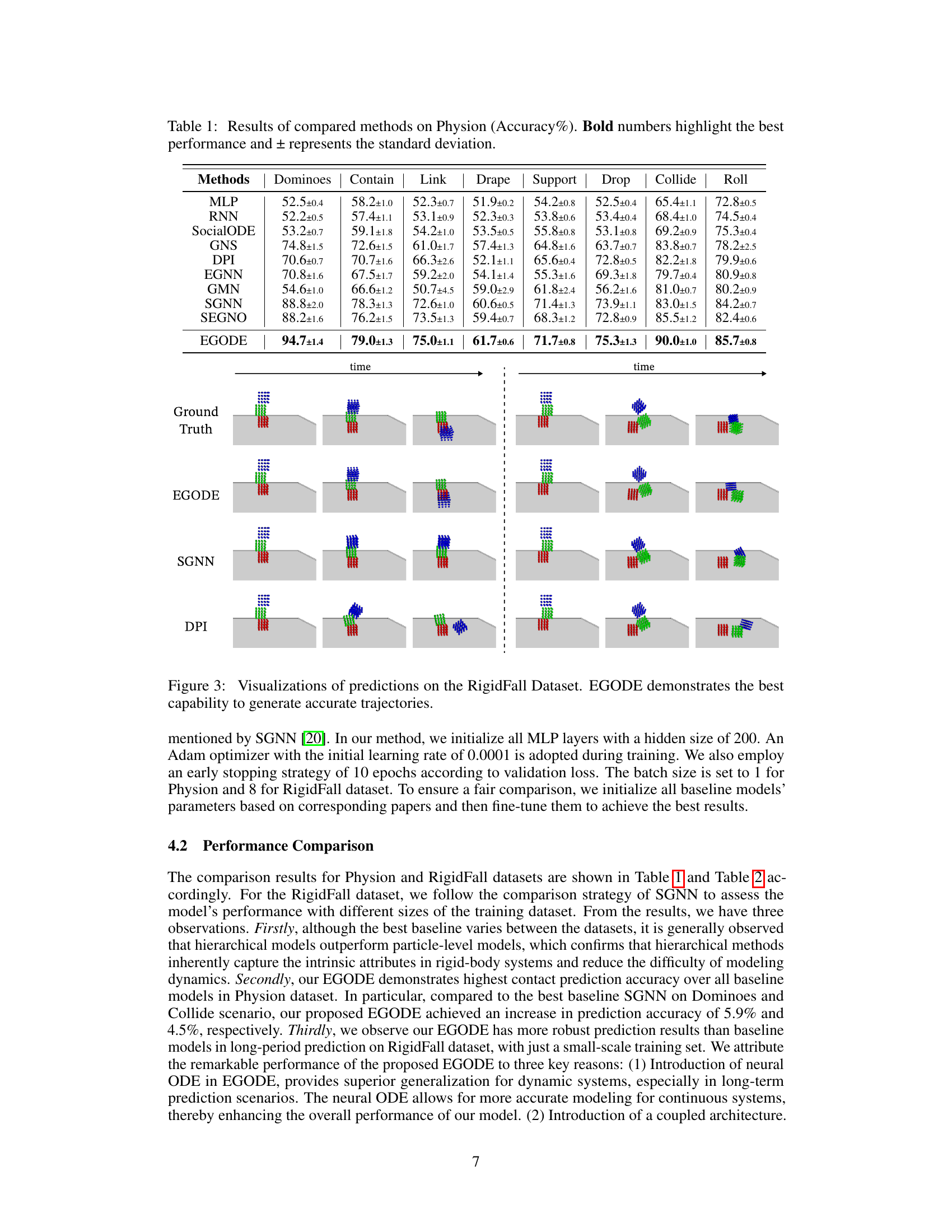
This table presents the accuracy results of different methods on the Physion dataset for various tasks (Dominoes, Contain, Link, Drape, Support, Drop, Collide, Roll). The accuracy is presented as a percentage, with the best performing method for each task shown in bold. The ± values indicate the standard deviation of the results, reflecting the variability in performance across different runs.

This table presents a comparison of the Mean Squared Error (MSE) achieved by different methods on the Physion dataset. The MSE is a measure of the difference between the predicted and actual values, so lower values indicate better performance. The methods compared include SGNN, SEGNO, and the authors’ proposed EGODE. The results are broken down by different scenarios within the Physion dataset: Dominoes, Collide, Roll, and Drape, showing the MSE for each method in each scenario. Bold numbers highlight the best-performing method for each scenario.
Full paper#