↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Adapting pre-trained vision-language models (VLMs) to new, unseen data (test-time adaptation) is crucial but challenging. Existing methods often adapt from a single modality (visual or textual) and fail to accumulate knowledge as more samples are processed. This limits their real-world applicability.
The proposed Dual Prototype Evolving (DPE) method tackles these issues using a novel multi-modal approach. It progressively evolves textual and visual prototypes, effectively accumulating task-specific knowledge. Learnable residuals align the prototypes, promoting consistent multi-modal representations and leading to superior performance. Extensive experiments demonstrate DPE’s consistent outperformance over state-of-the-art methods across 15 benchmark datasets with enhanced computational efficiency.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on vision-language models (VLMs) and test-time adaptation. It offers a novel approach to improve VLM generalization to unseen data, a significant challenge in real-world applications. The proposed method, Dual Prototype Evolving (DPE), is highly efficient and outperforms existing methods, opening avenues for further research on multi-modal adaptation and cumulative learning in VLMs.
Visual Insights#
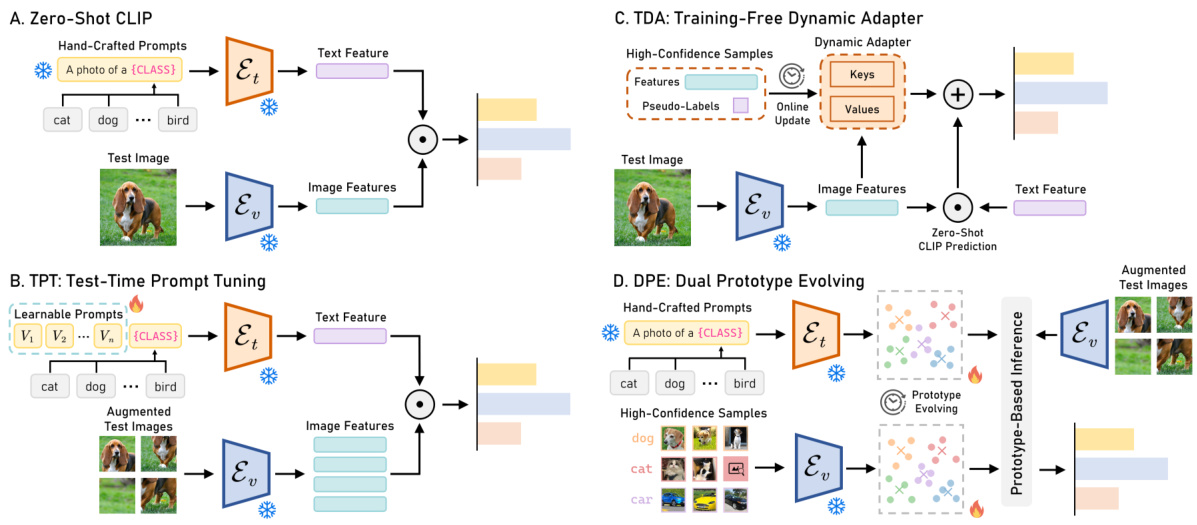
This figure compares four different methods for adapting vision-language models (VLMs) during test time. Zero-shot CLIP uses hand-crafted prompts, while TPT adapts prompts. TDA uses a dynamic adapter that incorporates high-confidence samples, and the proposed DPE method evolves prototypes from both textual and visual modalities to progressively improve multi-modal representations for target classes.
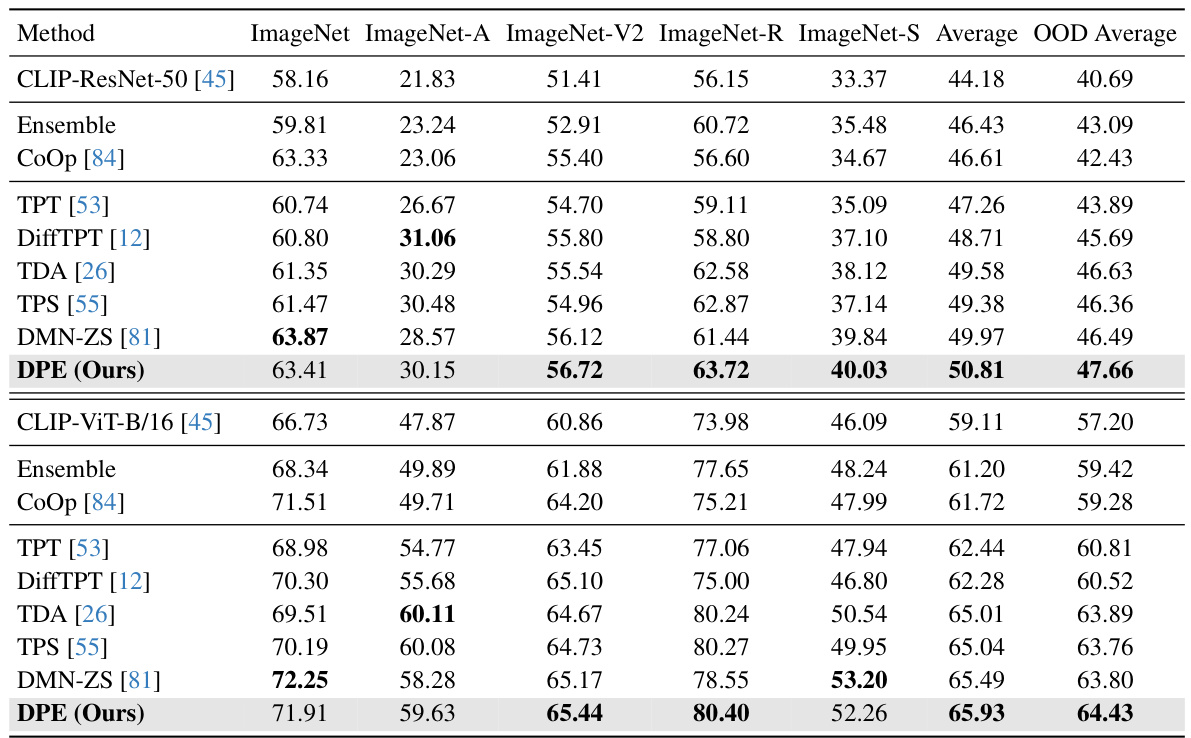
This table presents a comparison of the performance of different methods on robustness to natural distribution shifts. The methods are evaluated using two different visual backbones from CLIP (ResNet-50 and ViT-B/16), and the results are reported as top-1 accuracy. The table includes various baselines (Ensemble, CoOp, TPT, DiffTPT, TDA, TPS, DMN-ZS) and the proposed DPE method. The best performance for each dataset is highlighted in bold.
In-depth insights#
Dual Proto Evolves#
The concept of “Dual Proto Evolves” suggests a system that iteratively refines two sets of prototypes, likely representing different modalities (e.g., text and visual features) to improve the model’s performance. This approach is particularly relevant to vision-language models, where understanding both textual and visual information is crucial. The “dual” aspect highlights the simultaneous evolution of these two sets of prototypes, possibly using feedback from each other to ensure consistency. The “evolving” component implies an online learning process, adapting the prototypes progressively using unlabeled data encountered during the testing phase. This contrasts with traditional training methods that rely on a fixed dataset, making this approach more suitable for real-world scenarios where data distribution might shift after the model’s training. The core idea is to accumulate task-specific knowledge over time, leading to improved generalization and robustness. This iterative refinement makes the system adaptable to dynamic environments and less sensitive to initial biases.
Multimodal Adapts#
The concept of “Multimodal Adapts” in a research paper would likely explore how models can effectively integrate and leverage information from multiple modalities, such as text, images, and audio. A key aspect would be the adaptability of these models to varying contexts or tasks, demonstrating robustness against distribution shifts. The paper might investigate techniques for efficiently fusing multimodal data, potentially involving attention mechanisms or other sophisticated architectures that allow the model to dynamically weigh different modalities based on their relative importance to a given task. Addressing the challenges of data scarcity and computational cost would be crucial. The research might compare different multimodal adaptation strategies, analyzing their performance across diverse datasets and under various conditions. The core discussion will probably revolve around how these adaptations enhance the model’s generalizability and performance in complex, real-world scenarios, providing practical implications beyond controlled settings. A focus on explainability and transparency will likely enhance the overall value of such research.
Test-Time VLM#
Test-time adaptation for Vision-Language Models (VLMs) presents a unique challenge and opportunity. Pre-trained VLMs excel at zero-shot tasks, but often struggle with real-world scenarios involving distribution shifts between training and test data. Test-time VLM adaptation seeks to leverage unlabeled test data to directly improve model performance without retraining or accessing original training data, making it crucial for practical deployment. This approach is particularly valuable given the cost and complexity of retraining massive VLMs for specific tasks. Key techniques, such as prompt tuning and prototype-based methods, aim to fine-tune aspects of the VLM during inference, capturing task-specific information from the test set and adapting model behavior to unseen data. Dual modality adaptation, using both visual and textual features, is an important area of research, leading to more robust and accurate models. The major challenges and trade-offs lie in computational efficiency and generalization capability of the adaptation methods, requiring careful consideration of both the adaptation method and the VLM architecture itself.
Benchmark Results#
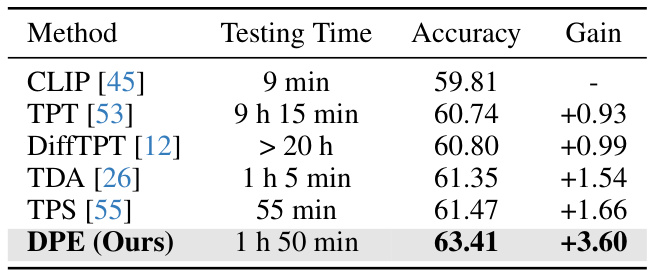
A dedicated ‘Benchmark Results’ section in a research paper would ideally present a comprehensive evaluation of the proposed method against state-of-the-art techniques. This would involve selecting relevant and established benchmarks, clearly defining evaluation metrics, and presenting results in a clear and easy-to-understand manner. Quantitative comparisons are crucial, showing performance gains or improvements over existing methods. A strong benchmark section would also include error bars or confidence intervals to demonstrate the statistical significance of the findings. Further enhancing its value would be ablation studies, systematically analyzing the effect of individual components or hyperparameters of the proposed method. Finally, a thoughtful discussion of the results, explaining any unexpected outcomes or limitations, would help establish the overall impact and significance of the contribution.
Future Directions#
Future research could explore more sophisticated prototype evolution strategies beyond simple averaging, potentially incorporating techniques from online learning or reinforcement learning. Investigating the impact of different prototype initialization methods on model performance is also warranted. A key area for future work is extending DPE to other VLM architectures and tasks beyond image classification. Furthermore, exploring the theoretical underpinnings of DPE’s success, perhaps via connections to established theoretical frameworks of test-time adaptation, would be beneficial. Finally, robustness evaluations on more diverse and challenging datasets, including those with complex noise patterns or significant domain shifts, are needed to solidify its practical applicability.
More visual insights#
More on figures
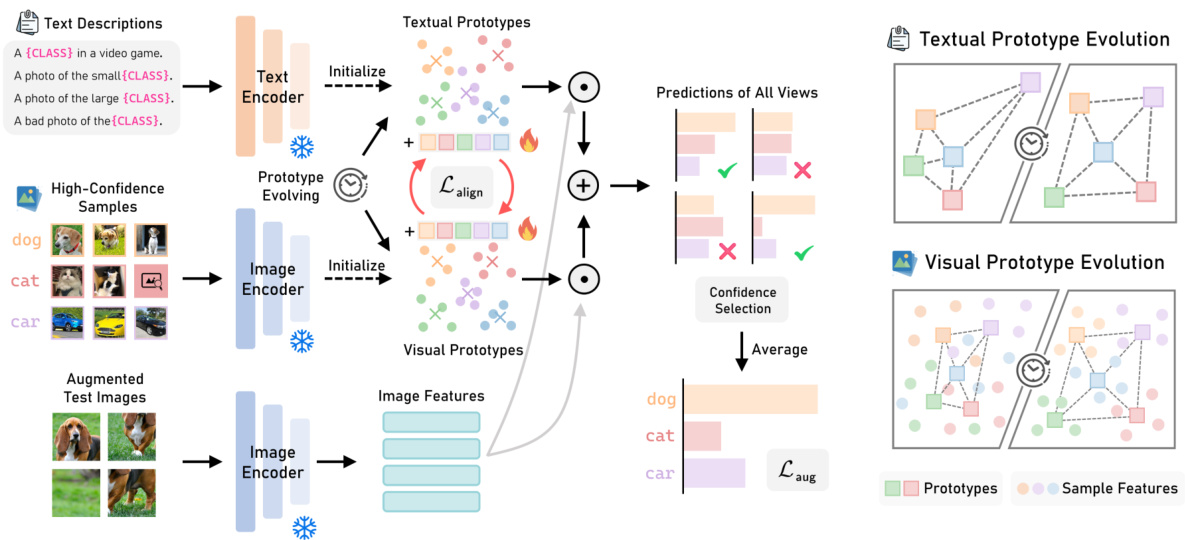
This figure illustrates the Dual Prototype Evolving (DPE) method. It shows how textual and visual prototypes are initialized, updated iteratively using high-confidence samples and learnable residuals, and used for prototype-based inference with CLIP. The alignment loss (Lalign) and self-entropy loss (Laug) are also shown, highlighting how the method ensures consistent multi-modal representations and minimizes self-entropy during the optimization process. Separate diagrams illustrate the evolution of both textual and visual prototypes over time.
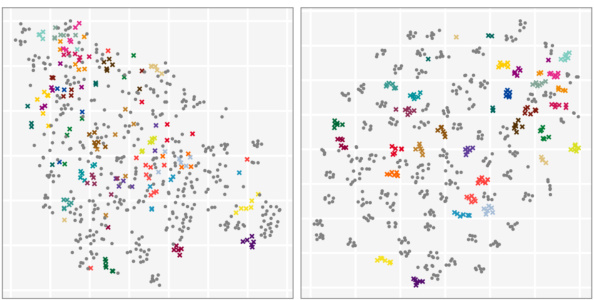
This figure shows t-SNE visualizations of image features stored in priority queues for different numbers of samples. The left panel shows the state after processing 1500 samples, and the right after 15000. The goal is to show that as more samples are added, the features for each class cluster closer together in the embedding space, resulting in better prototypes for classification. Different colors represent different classes. Gray points represent features that were not selected for the prototypes.
This figure illustrates the Dual Prototype Evolving (DPE) method. It shows how textual and visual prototypes are initialized, updated iteratively using high-confidence samples, and refined using learnable residuals. The process aims to create accurate multi-modal representations for better classification.
More on tables
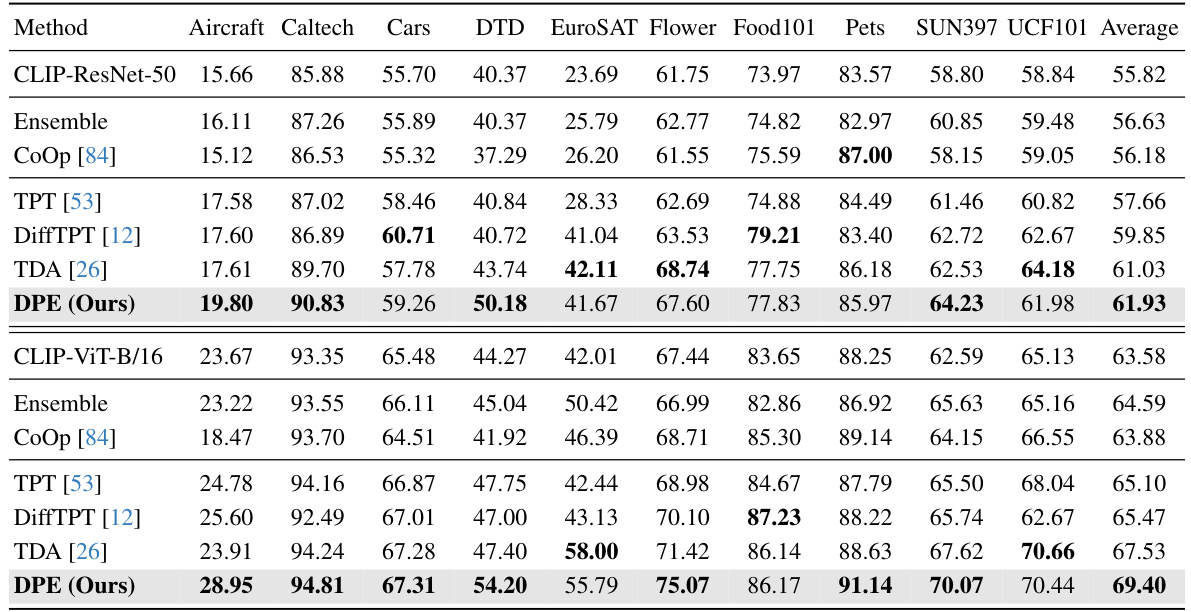
This table compares the performance of different methods on robustness to natural distribution shifts using two different visual backbones (ResNet-50 and ViT-B/16) for the CLIP model. It shows top-1 accuracy results across several ImageNet variations (ImageNet-A, ImageNet-V2, ImageNet-R, ImageNet-S) designed to test out-of-distribution generalization. The average accuracy across these variations and the average out-of-distribution accuracy are also given. The best performance for each backbone is highlighted in bold.
This table presents a comparison of the performance of several methods on the task of adapting vision-language models (VLMs) to handle out-of-distribution data. The methods are evaluated on several benchmark datasets (ImageNet, ImageNet-A, ImageNet-V2, ImageNet-R, ImageNet-S) that represent different types of distribution shifts. The accuracy is reported using two different visual backbones for the CLIP model (ResNet-50 and ViT-B/16).

This table presents a comparison of the proposed Dual Prototype Evolving (DPE) method with other state-of-the-art methods on robustness to natural distribution shifts. The performance is evaluated using two different visual backbones from CLIP (ResNet-50 and ViT-B/16), and the top-1 accuracy is reported for each method across five different ImageNet datasets (ImageNet, ImageNet-A, ImageNet-V2, ImageNet-R, and ImageNet-S) and an out-of-distribution (OOD) average. The best-performing method for each dataset and average is highlighted in bold.

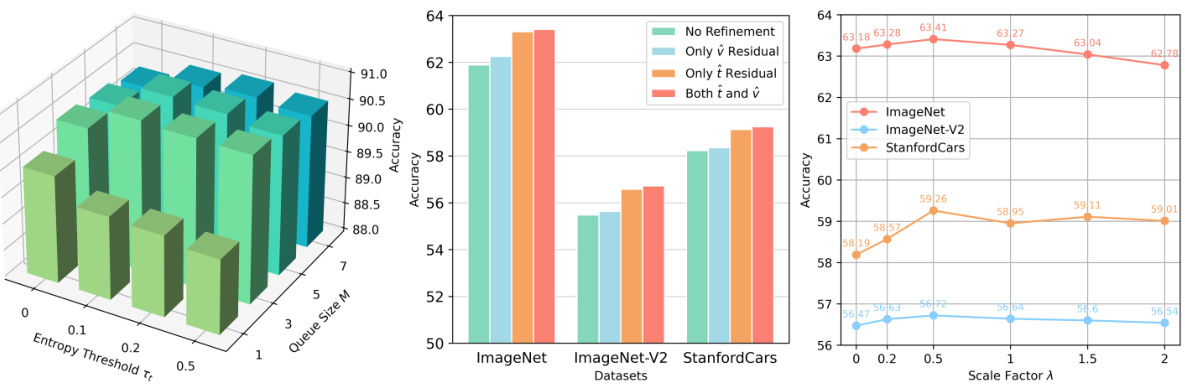
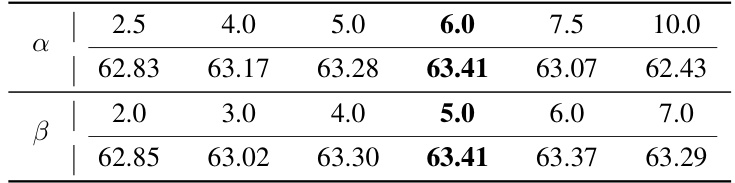
This table presents an ablation study on the impact of varying the number of update steps in the prototype residual learning component of the proposed DPE method. The experiment is conducted on the ImageNet dataset. The table shows that a single update step provides the best performance, with marginal improvements seen when increasing to two steps but a decrease in performance with more than two steps.
This table presents a comparison of the performance of different methods on robustness to natural distribution shifts. It shows top-1 accuracy results for various methods using two different visual backbones (ResNet-50 and ViT-B/16) in CLIP. The methods compared include baseline CLIP, ensemble methods, prompt learning methods, adapter methods, and the proposed DPE method. The results are presented for different ImageNet datasets, including ImageNet-A, ImageNet-V2, ImageNet-R, and ImageNet-S, which represent various out-of-distribution scenarios. The best-performing method for each scenario is highlighted in bold.

This table compares the performance of different methods on ImageNet and its out-of-distribution variants (ImageNet-A, ImageNet-V2, ImageNet-R, ImageNet-S). It shows the top-1 accuracy for each method using two different backbones (ResNet-50 and ViT-B/16) of the CLIP model. The table highlights the best-performing method for each dataset and backbone combination. It helps to understand the robustness of different approaches to distribution shifts.

This table presents a comparison of the performance of different methods on robustness to natural distribution shifts using the larger-scale ViT-L/14 visual backbone of OpenCLIP. The methods compared include TDA and the authors’ proposed DPE method. The table shows the top-1 accuracy for each method across five ImageNet datasets (ImageNet, ImageNet-A, ImageNet-V2, ImageNet-R, ImageNet-S), along with the average accuracy across these datasets and a separate average OOD (out-of-distribution) accuracy. The best performance for each dataset is highlighted in bold.

This table presents a comparison of different methods on their robustness to natural distribution shifts. The top-1 accuracy is shown for ResNet-50 and ViT-B/16 backbones of CLIP. Results are also included for methods using prompts learned by CoOp (a train-time adaptation method) to show the impact of training data. The best-performing method for each setting is highlighted in bold.

This table presents an ablation study evaluating the individual contribution of each component of the Dual Prototype Evolving (DPE) method. It shows the top-1 accuracy on ImageNet when using different combinations of visual prototype evolution (VPE), textual prototype evolution (TPE), and prototype residual learning (PRL). The results demonstrate the significant impact of VPE, while also highlighting the positive contributions of TPE and PRL.

This table shows the ablation study of the two loss functions used in the Dual Prototype Evolving (DPE) method. It compares the ImageNet top-1 accuracy using only the self-entropy loss, only the alignment loss, and both losses combined. The results demonstrate the contribution of each loss to the overall performance.
This table presents a comparison of the performance of different methods on the task of robustness to natural distribution shifts. The methods are evaluated using two different backbones (ResNet-50 and ViT-B/16) from the CLIP model. The results, shown as top-1 accuracy percentages, demonstrate how well each method generalizes to out-of-distribution data. The best-performing method for each dataset is highlighted in bold.
This table compares the performance of the proposed Dual Prototype Evolving (DPE) method with other state-of-the-art methods on robustness to natural distribution shifts. The comparison uses two different backbones for the CLIP model (ResNet-50 and ViT-B/16), and evaluates performance on several ImageNet variants (ImageNet-A, ImageNet-V2, ImageNet-R, and ImageNet-S), as well as an out-of-distribution (OOD) average. The best performing method for each setting is highlighted in bold. The table demonstrates DPE’s improved accuracy compared to other methods.
Full paper#