↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world decision-making problems involve hidden information, making them challenging to model using standard reinforcement learning (RL) techniques. These scenarios are often modeled as latent Markov decision processes (LMDPs), but solving LMDPs efficiently has been a significant hurdle. Existing algorithms either require strong assumptions or suffer from the ‘curse of horizon’, meaning their performance degrades drastically as the time horizon increases. This research addresses these challenges.
This research introduces a novel algorithm that solves the exploration problem in LMDPs without any extra assumptions or distributional requirements. It does so by establishing a new theoretical connection between off-policy evaluation and exploration in LMDPs. Specifically, they introduce a new coverage coefficient to analyze the performance of their algorithm, demonstrating its efficiency and near-optimality. This approach offers a fresh perspective that goes beyond the limitations of traditional methods, and the result is a sample-efficient algorithm with provably near-optimal guarantees.
Key Takeaways#
Why does it matter?#
This paper is crucial because it solves a long-standing problem in reinforcement learning, specifically addressing the challenge of efficient exploration in latent Markov decision processes (LMDPs). The results break the “curse of horizon”, opening new avenues for tackling complex real-world problems with hidden information, and provides valuable new theoretical tools applicable to other partially observed environments.
Visual Insights#
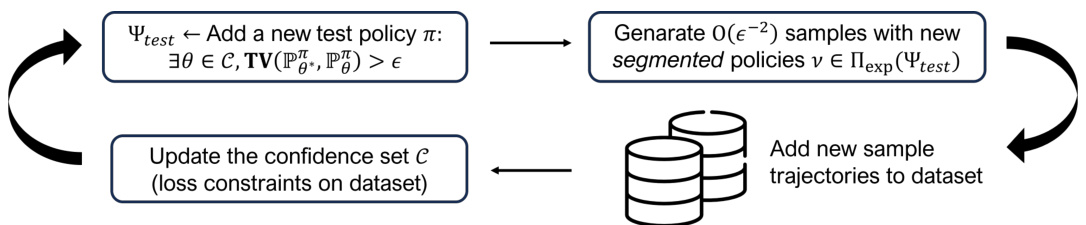
This figure shows a high-level overview of the LMDP-OMLE algorithm. The algorithm iteratively refines a confidence set of models. In the online phase, it finds a new test policy that reveals disagreement among the models in the confidence set. It then constructs an exploration policy using the new concept of segmented policies, executing multiple policies sequentially, potentially incorporating random actions at specific checkpoints. In the offline phase, the algorithm updates the confidence set by incorporating new data generated during the online exploration phase.

This table illustrates a counter-example where single latent-state coverability is insufficient for off-policy evaluation guarantees in LMDPs. It shows four possible initial histories (combinations of action a1 and reward r1) that could result from one of three possible latent contexts (m). For each history, the table shows the expected reward (E[r2]) for actions a2=1 and a2=2 at the next time step. The table demonstrates that even when all state-action pairs are covered under all contexts, it is still impossible to estimate the expected reward E[r2] from some histories, thus highlighting the necessity of using multi-step coverability in the analysis.
Full paper#



















