↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Large language models (LLMs) are powerful but computationally expensive, hindering real-world applications. Existing compression methods often lead to suboptimal performance due to uniform pruning and ignoring the varying importance of features across different layers.
This paper introduces Adaptive Layer Sparsity (ALS), a novel method that addresses these limitations. ALS leverages information orthogonality to evaluate layer importance, then uses a linear optimization algorithm for adaptive sparse allocation. Experiments on various LLMs (LLaMA, OPT) across multiple benchmarks demonstrate ALS’s effectiveness, surpassing state-of-the-art methods in performance, even at high sparsity levels. ALS provides a more efficient and effective LLM compression strategy.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel and effective method for compressing large language models (LLMs) without sacrificing performance. This addresses a critical challenge in deploying LLMs in real-world applications, where resource constraints are a major concern. The method’s superiority over existing approaches, demonstrated through extensive experiments, makes it a significant contribution to the field. It opens new avenues for research into efficient LLM optimization and resource management, paving the way for wider accessibility and adoption of LLMs.
Visual Insights#
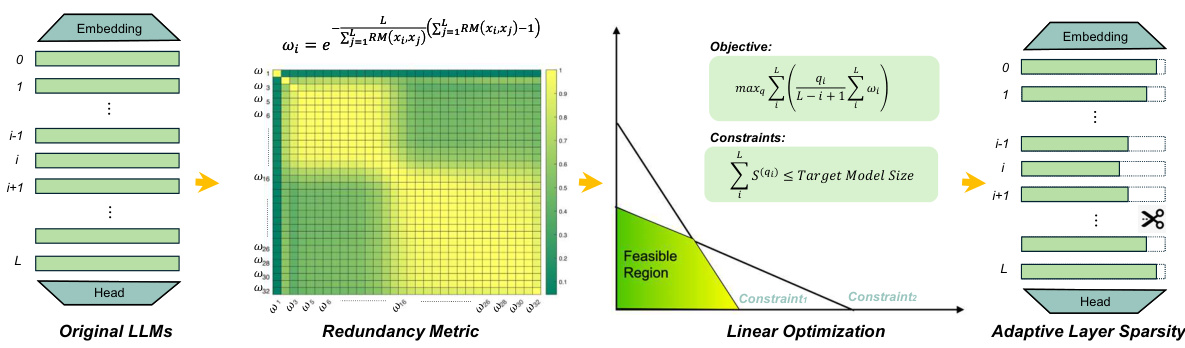
This figure illustrates the Adaptive Layer Sparsity (ALS) framework. First, a redundancy metric is calculated between each layer and all other layers of the Large Language Model (LLM). This metric quantifies the redundancy or importance of each layer. Then, a linear programming problem is formulated and solved. The objective function maximizes the overall sparsity of the model, subject to constraints on the total model size. The solution to this optimization problem determines the optimal sparsity ratio for each layer, which is then applied to selectively prune less important features, resulting in an adaptively sparse model.

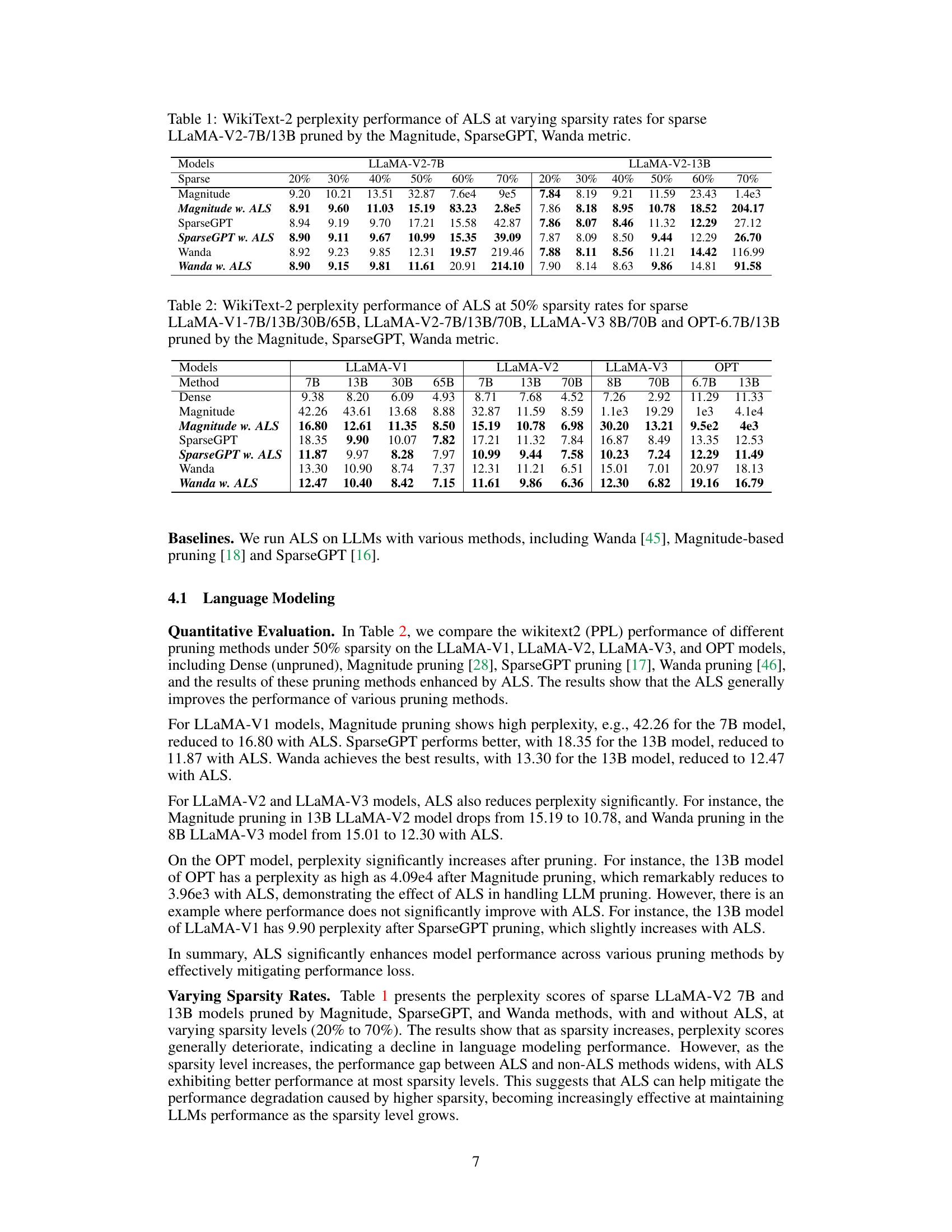
This table presents the WikiText-2 perplexity scores achieved by applying Adaptive Layer Sparsity (ALS) to various LLaMA-V2 models (7B and 13B parameters) that were initially pruned using three different methods (Magnitude, SparseGPT, and Wanda). It demonstrates how ALS improves the perplexity (a measure of language model performance) at different sparsity levels (20% to 70%) across these different pruning baselines.
In-depth insights#
Adaptive Sparsity#
Adaptive sparsity, in the context of large language models (LLMs), presents a powerful paradigm shift from traditional uniform pruning methods. Instead of indiscriminately removing weights or neurons across all layers, adaptive sparsity intelligently analyzes the significance of each layer and allocates sparsity ratios accordingly. This nuanced approach leverages techniques like correlation assessment to identify layers or components with high redundancy or low information gain, selectively pruning them for greater efficiency. The key advantage lies in maintaining model performance while achieving significant compression. By focusing on less critical parts of the model, adaptive sparsity avoids the suboptimal performance often associated with uniform pruning strategies. The superior performance compared to prior methods highlights the value of this targeted, intelligent compression. The development of effective methods for determining the significance of different layers is critical to the success of adaptive sparsity. Advanced techniques, such as analyzing mutual information and information orthogonality, may play an integral role in future advancements. This approach offers a promising avenue towards making LLMs more accessible and efficient.
Correlation Metric#
A correlation metric in the context of a research paper on large language model (LLM) optimization likely quantifies the statistical dependence between different layers of the model. High correlation suggests redundancy, implying that certain layers might be pruned without significant performance loss. Conversely, low correlation indicates complementary information, suggesting that preserving all such layers is crucial for optimal performance. The choice of metric depends on the specific properties being investigated; mutual information, for instance, measures the shared uncertainty between layers, while other metrics might focus on linear or non-linear relationships. The effectiveness of the metric is crucial for the success of any layer-wise sparsity optimization technique, as it guides the selective pruning or compression of model layers. The accuracy of the correlation metric directly impacts the efficiency and performance gains achieved by the proposed LLM optimization.
Linear Optimization#
The heading ‘Linear Optimization’ suggests a crucial methodological step in the paper. It likely describes how the authors formulate the problem of achieving adaptive layer sparsity as a linear programming problem. This approach is significant because linear programming offers efficient algorithms for finding optimal solutions, even within complex, high-dimensional spaces. The authors’ choice to model the sparsity allocation problem in this way likely stems from a desire to find a globally optimal solution instead of resorting to heuristic or greedy methods that may get stuck in local optima. By framing the sparsity allocation as a linear program, they can leverage the power of well-established optimization techniques. The constraints of this linear program likely involve limiting the total number of parameters after pruning to meet a target model size, thus balancing efficiency with accuracy. The objective function would likely involve maximizing the independence between the layers, as measured by the Redundancy Metric developed earlier in the paper. The successful application of linear programming to this problem could provide a significant contribution, demonstrating the effectiveness and scalability of this approach to model compression for large language models.
LLM Efficiency#
Large Language Models (LLMs) are revolutionizing various fields, but their enormous size poses significant challenges for real-world applications. LLM efficiency is paramount, demanding innovative approaches to reduce computational costs and memory footprint without sacrificing performance. This involves exploring various compression techniques such as pruning, quantization, and knowledge distillation. However, uniform approaches often prove suboptimal due to the varying importance of features across different layers. Adaptive methods, which consider the unique characteristics of each layer, are crucial for effective compression. The optimal balance between compression and performance is a complex optimization problem requiring careful consideration of factors like sparsity levels, redundancy metrics, and fine-tuning strategies. Future research should explore theoretical foundations to guide the development of more effective and robust LLM efficiency techniques, thereby enabling wider deployment and utilization of these powerful models.
Future Research#
Future research directions stemming from this Adaptive Layer Sparsity (ALS) method could explore several promising avenues. Firstly, a deeper investigation into the theoretical underpinnings of ALS is warranted. While the method demonstrates strong empirical results, a more robust theoretical framework justifying its effectiveness and explaining why it surpasses other approaches would significantly strengthen its impact. Secondly, the exploration of different sparsity allocation strategies beyond the linear optimization currently employed in ALS would be beneficial. Investigating non-linear methods or incorporating additional factors like layer depth or computational cost into the optimization process could further enhance performance and efficiency. Thirdly, the scalability of ALS to even larger language models (LLMs) should be tested rigorously. Currently, the computational cost of ALS is reasonable, however, ensuring its efficiency for models with hundreds of billions of parameters remains a crucial challenge. Finally, researchers could explore the integration of ALS with other LLM compression techniques. Combining ALS with quantization or knowledge distillation methods could result in synergistic benefits, achieving further gains in model size reduction without compromising accuracy. Addressing these future directions would contribute towards a more comprehensive understanding and broader adoption of adaptive sparsity methods for LLMs.
More visual insights#
More on figures

This figure presents three subplots visualizing the impact of different factors on the performance of the language model. (a) shows how perplexity decreases slightly as the amount of calibration data increases; (b) illustrates the model’s stable performance when pruning bounds are between 30% and 70%; and (c) demonstrates that higher redundancy metrics correlate with lower performance.
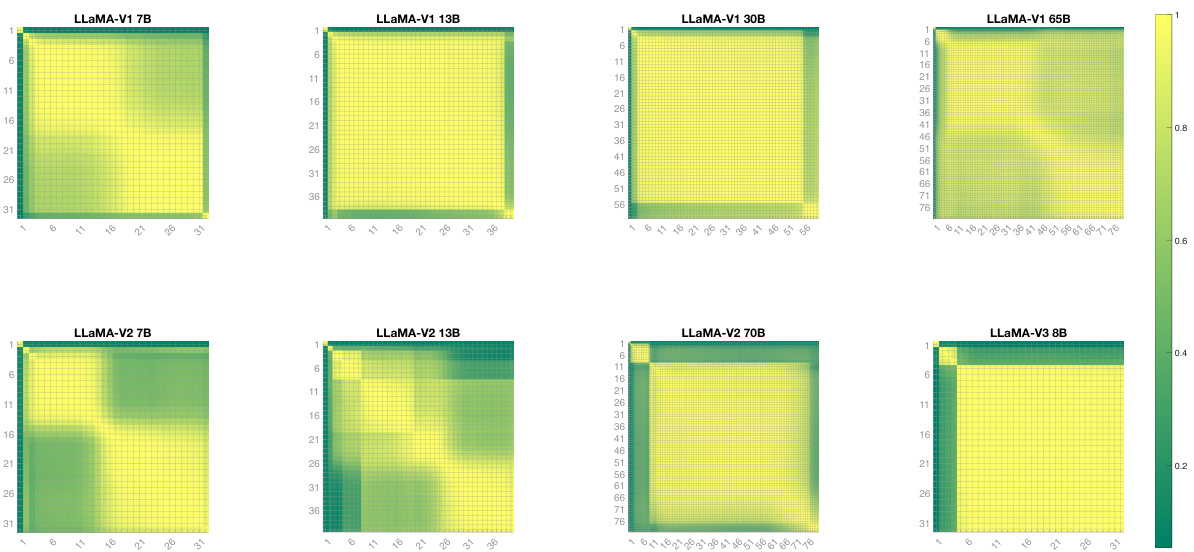
This figure visualizes the correlation matrices obtained by solving the problem under different experimental settings. It shows the heatmaps of the Redundancy Metric (RM) for various LLMs (LLaMA-V1 7B, 13B, 30B, 65B; LLaMA-V2 7B, 13B, 70B; LLaMA-V3 8B) at different sparsity levels (50% for the first set of models, and various levels for the second set of models). The color intensity represents the redundancy between layers, with darker colors indicating higher redundancy.

This figure visualizes the correlation matrices obtained by solving the redundancy problem using the proposed method for different LLMs at various sparsity levels. Specifically, it showcases heatmaps representing the Redundancy Metric (RM) for different models, illustrating the correlation between layers. The color intensity in the heatmaps indicates the level of redundancy, with darker shades representing higher redundancy and lighter shades representing lower redundancy.

This figure visualizes the correlation matrices obtained by solving the linear programming problem in the ALS method, showing the redundancy among layers in different LLMs at various sparsity levels (50% for LLaMA-V1/V2/V3 and various levels for LLaMA-V2 7B/13B). The heatmaps represent the Redundancy Metric (RM), with darker colors indicating higher redundancy between layers. The figure aims to illustrate how the proposed ALS method effectively allocates sparsity ratios across different layers based on their redundancy, achieving fine-grained optimization of LLMs.

This figure visualizes the sparsity ratio allocation across different layers of LLAMA-V2 7B and 13B models at various sparsity levels (30%, 40%, 50%, 60%, 70%). Each sub-figure represents a specific model and sparsity level, showing the allocated sparsity ratio for each layer (Q, K, V, O, gate, up, down) using a color gradient. The color intensity represents the sparsity ratio, with darker shades indicating higher sparsity.
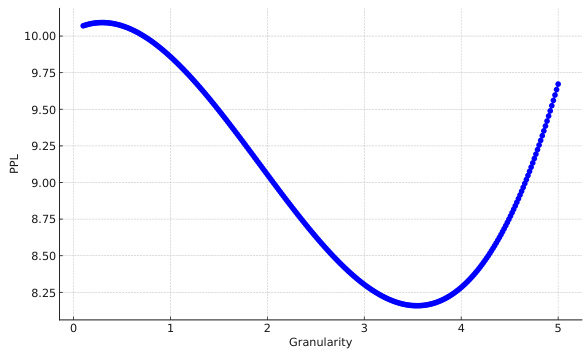
The figure shows the result of an experiment on the impact of granularity on perplexity (PPL) in the LLAMA-V2 7B model. Initially, PPL remains relatively constant for granularities of 0.1 and 0.5. It then decreases to 9.86 at a granularity of 1 and further to 9.67 at a granularity of 5. Beyond this point, the smoothed curve shows a subsequent rise in PPL, indicating that excessively high granularity may negatively impact model performance. This illustrates a necessary balance in optimizing granularity to minimize PPL and enhance model accuracy and efficiency.

This figure compares two different decreasing functions used in the paper’s Adaptive Layer Sparsity (ALS) method. The x-axis represents the sum of redundancy metrics between a layer and other layers. The y-axis represents the importance factor (wi) calculated by each function. The original expression shows a steeper decline, suggesting a more aggressive reduction in importance as redundancy increases. The modified expression exhibits a gentler decrease, which might offer a more balanced adjustment to sparsity ratios across layers. This choice of functions impacts the distribution of sparsity across the layers of the language model and is a crucial element of the ALS algorithm.

This figure compares two different decreasing functions used in the Adaptive Layer Sparsity (ALS) method for allocating sparsity ratios across layers. The original expression, ωi = exp(−(∑j≠iRM(xi,xj)−1)), is compared against a modified expression. The x-axis represents the sum of redundancy metrics (RM) between a given layer and other layers, while the y-axis represents the resulting importance weight (ωi) for that layer. The plot shows how the different functions transform the redundancy values into importance weights, highlighting the impact of the function choice on the sparsity allocation.
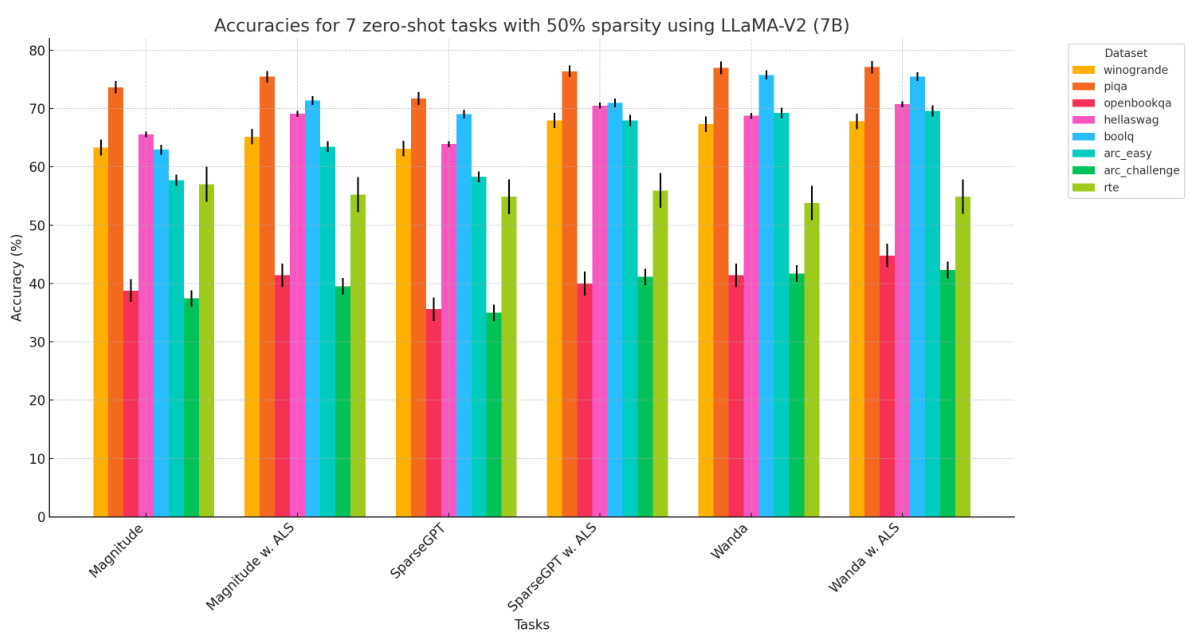
This figure shows the error bars for the accuracy of seven zero-shot tasks using the LLaMA-V2 7B model with 50% sparsity. The error bars represent the standard deviation of multiple runs of the experiments, providing a measure of the variability in the results. The tasks are winogrande, piqa, openbookqa, hellaswag, boolq, arc-easy, arc-challenge, and rte. The different colored bars represent the different pruning methods: Magnitude, Magnitude with ALS, SparseGPT, SparseGPT with ALS, Wanda, and Wanda with ALS.

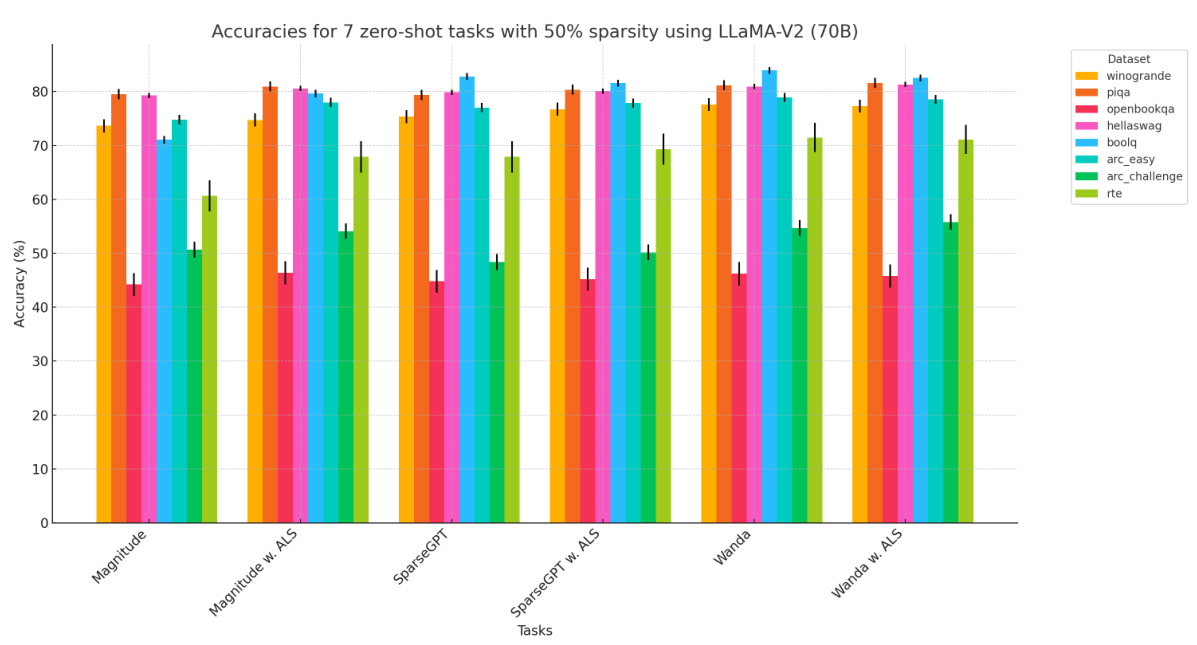
This figure presents the results of three experiments evaluating different aspects of the proposed Adaptive Layer Sparsity (ALS) method. (a) shows that increasing the amount of calibration data leads to a small decrease in perplexity (PPL), demonstrating the robustness of ALS. (b) shows that model performance is stable when the pruning bounds are set between 30% and 70%, which is a practical range for efficient pruning. (c) demonstrates a negative correlation between model redundancy and PPL, suggesting that minimizing redundancy is essential for improving the model’s performance.
This figure presents the results of three experiments analyzing the impact of different factors on the performance of the proposed Adaptive Layer Sparsity (ALS) method. (a) shows the relationship between the amount of calibration data used and the perplexity (PPL) score, indicating a slight improvement with increased data but a limited effect. (b) demonstrates the relative stability of model performance across a range of pruning bounds (30% to 70%), suggesting the robustness of the method. (c) illustrates a negative correlation between model redundancy (measured using the Redundancy Metric or RM) and model performance (PPL), highlighting that minimizing redundancy leads to improved performance.
More on tables
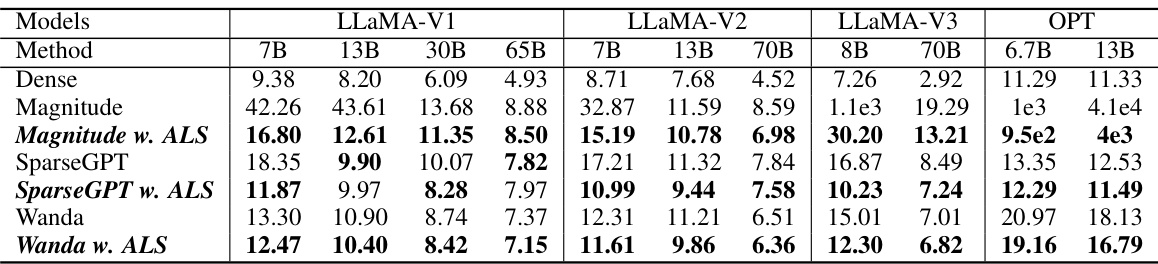
This table presents the WikiText-2 perplexity scores achieved by different sparse language models (LLaMA-V1, LLaMA-V2, LLaMA-V3, and OPT) at a 50% sparsity rate. The models were pruned using three different methods: Magnitude, SparseGPT, and Wanda. The table shows the perplexity of each model before and after applying the Adaptive Layer Sparsity (ALS) method, illustrating the impact of ALS on model performance.

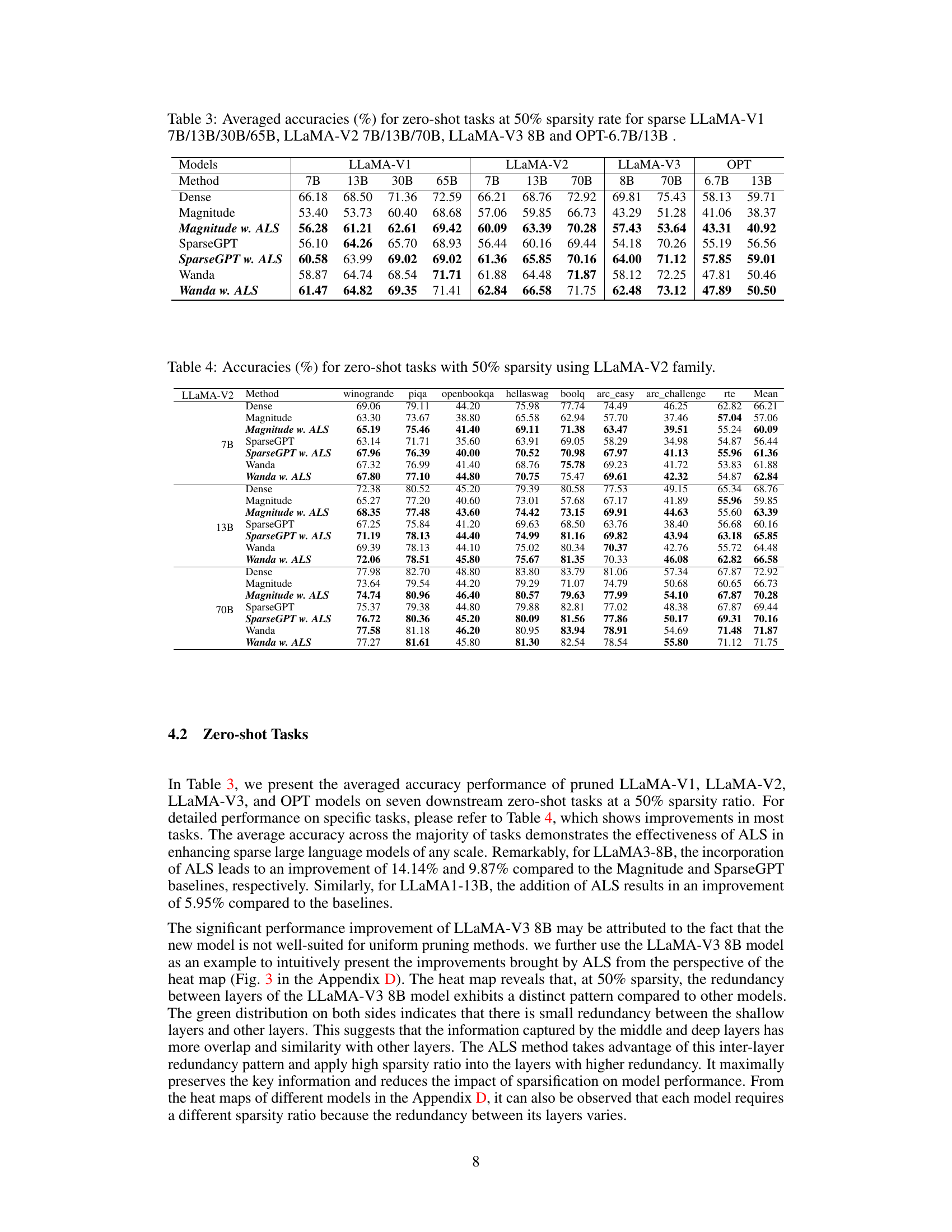
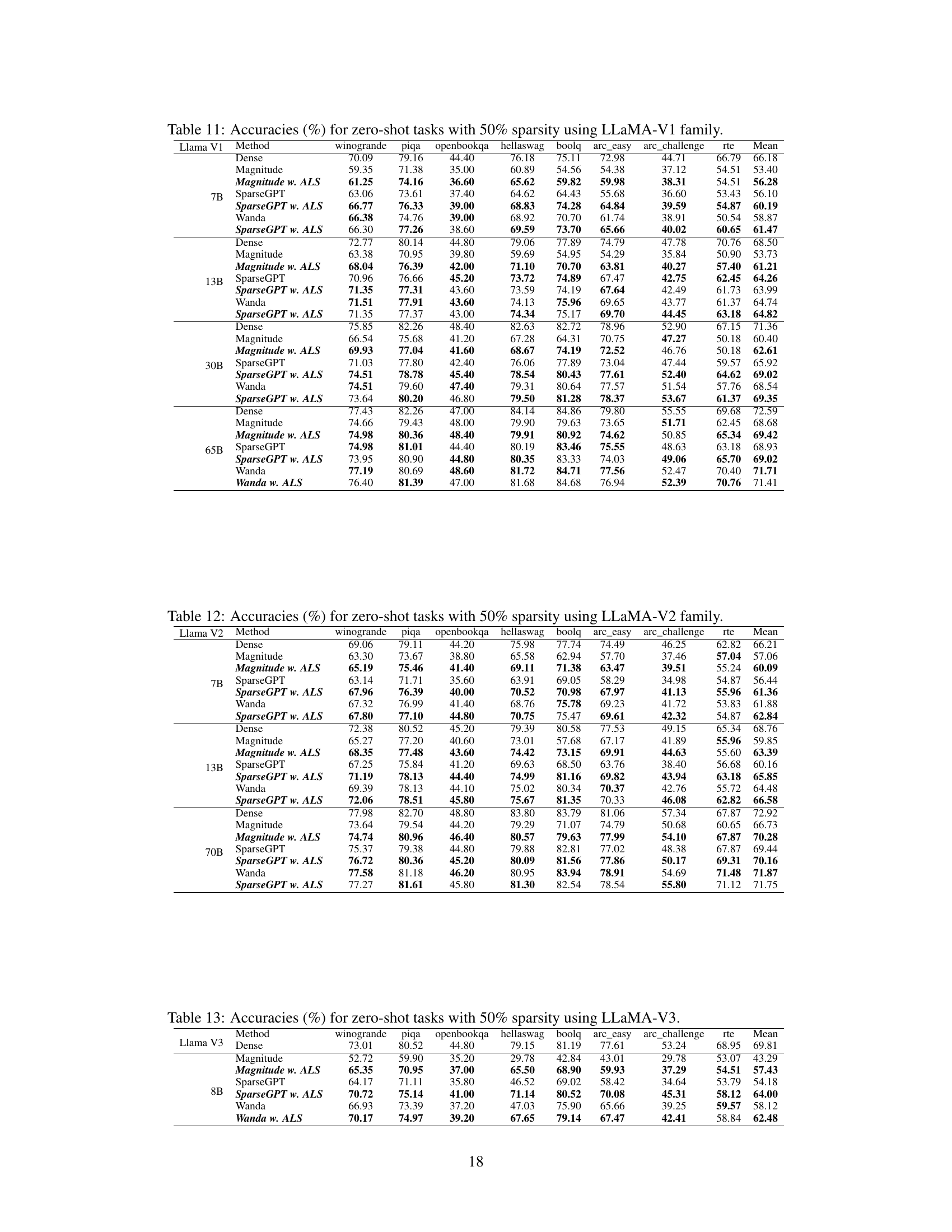
This table presents the average accuracy across seven zero-shot tasks for various LLMs (LLaMA-V1, LLaMA-V2, LLaMA-V3, and OPT) at a 50% sparsity rate. The results are compared across different pruning methods (Dense, Magnitude, Magnitude w. ALS, SparseGPT, SparseGPT w. ALS, Wanda, and Wanda w. ALS). The table shows the impact of the ALS method on the accuracy of sparse LLMs.

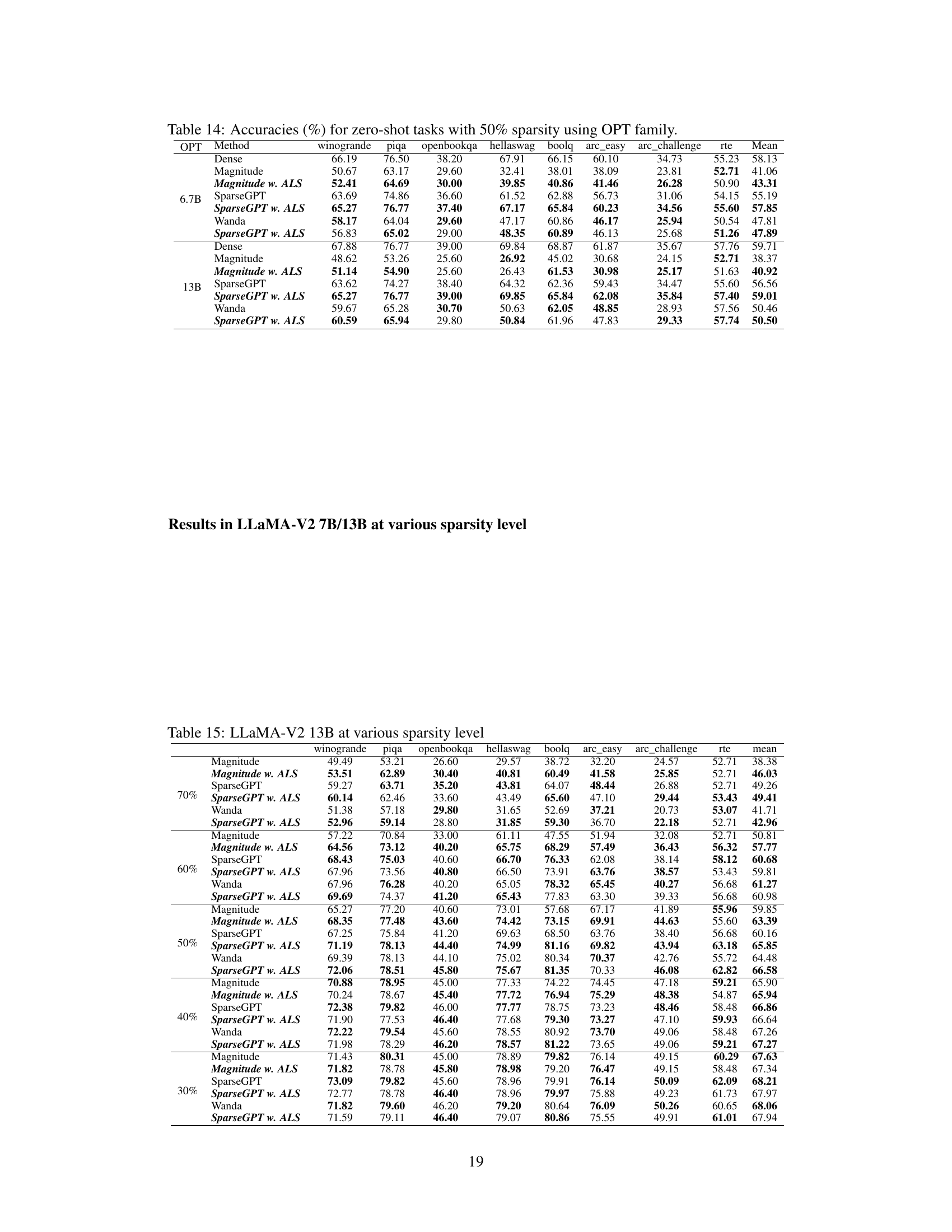
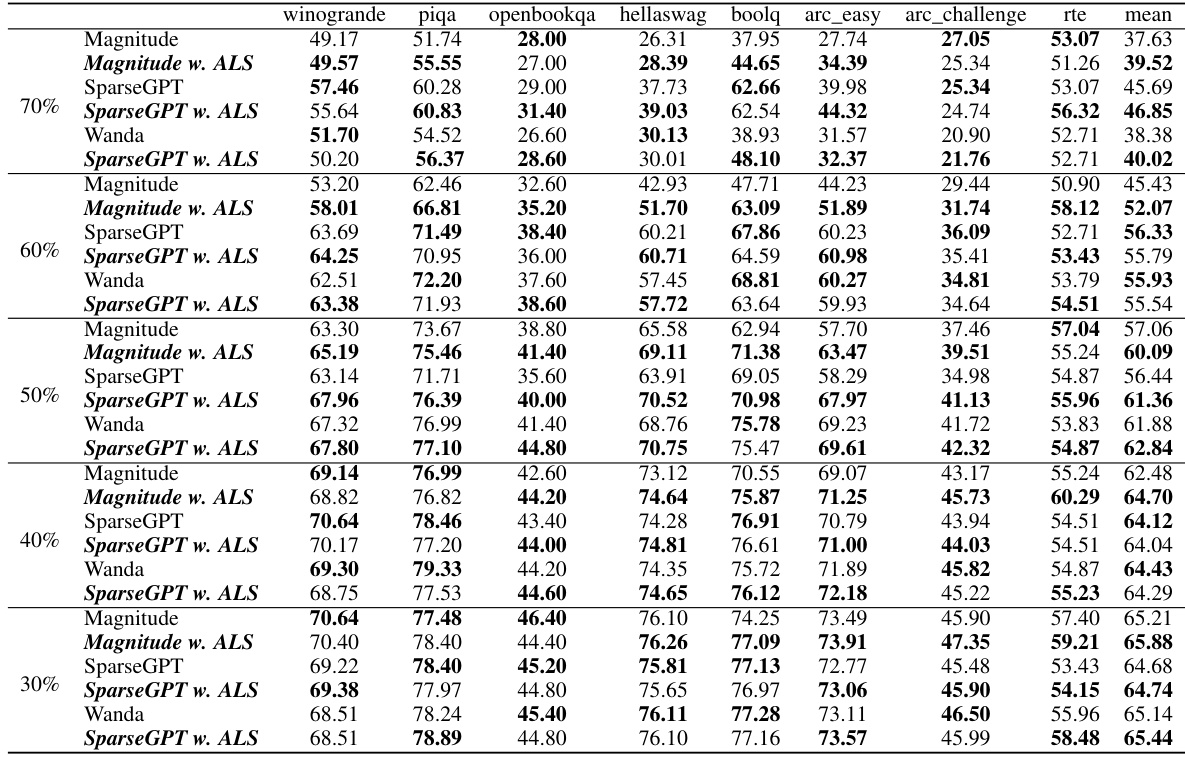
This table presents the average accuracy across seven zero-shot tasks for various large language models (LLMs) at 50% sparsity. It compares the performance of different pruning methods (Magnitude, SparseGPT, Wanda) with and without the Adaptive Layer Sparsity (ALS) approach. The results show the impact of ALS on the performance of different LLMs under the condition of high sparsity.

This table presents the WikiText-2 perplexity results for various large language models (LLMs) after applying adaptive layer sparsity (ALS) at a 50% sparsity rate. It compares the performance of ALS against three baseline pruning methods (Magnitude, SparseGPT, and Wanda) across different LLM sizes and architectures, showcasing the impact of ALS on perplexity scores.
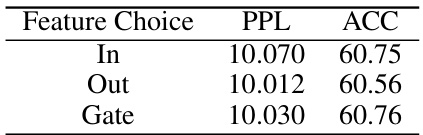
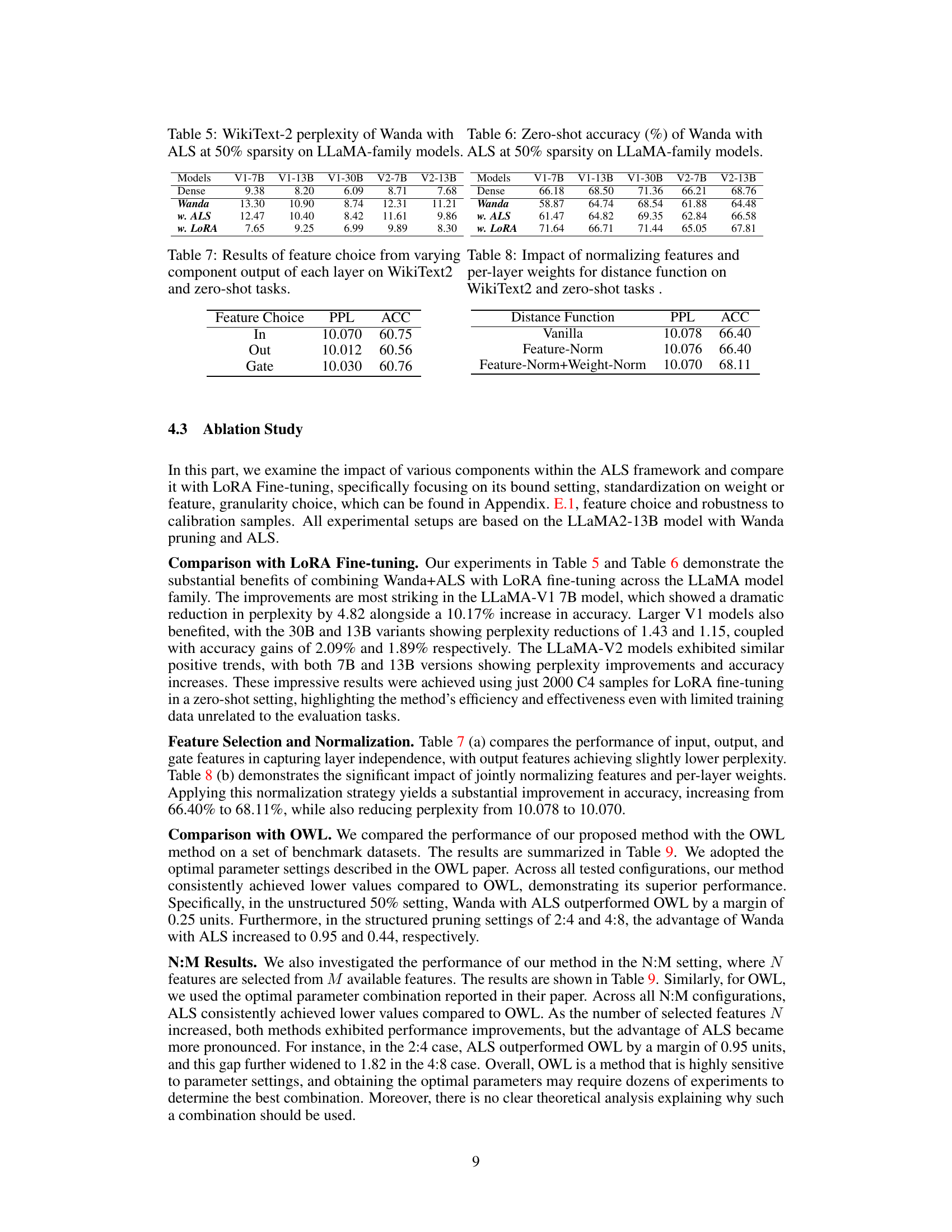
This table presents the results of an ablation study that investigates the impact of different feature choices (input, output, gate) on the performance of the model in terms of perplexity (PPL) on the WikiText-2 dataset and accuracy (ACC) on zero-shot tasks. It shows how the choice of features affects the model’s ability to learn representations and generalize to new tasks.

This table presents the results of an ablation study on the impact of feature and weight normalization on the performance of the proposed method. It compares the WikiText-2 perplexity (PPL) and average accuracy (ACC) across three different settings: using no normalization (Vanilla), normalizing only features (Feature-Norm), and normalizing both features and weights (Feature-Norm+Weight-Norm). The results show that applying feature and weight normalization leads to improvements in accuracy, while perplexity remains relatively stable.

This table presents the WikiText-2 perplexity scores achieved by the Wanda model with and without ALS (Adaptive Layer Sparsity) and OWL (Outlier Weighed Layerwise Sparsity) at different sparsity levels (50%, 2:4, 4:8). It demonstrates the comparative performance of these different sparsity allocation methods on a specific LLM model and benchmark dataset, highlighting the effectiveness of ALS.
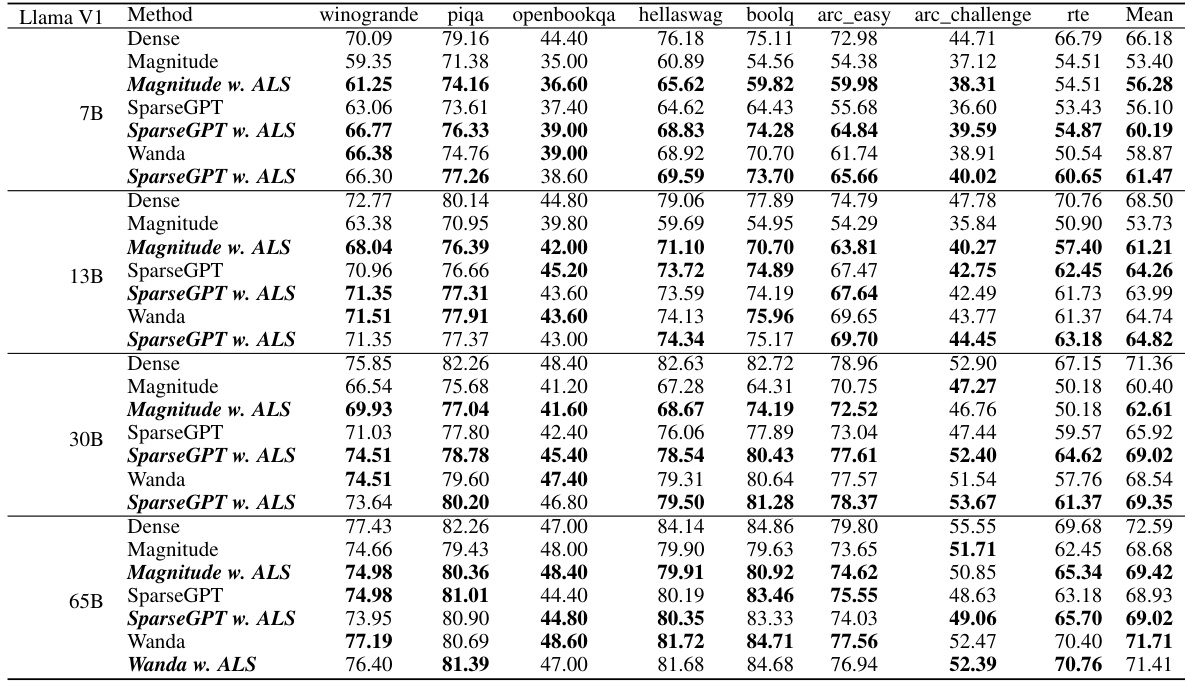
This table presents the average accuracy across seven zero-shot tasks for various large language models (LLMs) at 50% sparsity. The models include different versions of LLaMA and OPT, each pruned using different methods (Magnitude, SparseGPT, Wanda) with and without the Adaptive Layer Sparsity (ALS) method. The table allows for comparison of the performance impact of ALS across different LLMs and pruning techniques.

This table presents the average accuracy across seven zero-shot tasks for various large language models (LLMs) at 50% sparsity. The results compare the performance of different pruning methods (Magnitude, SparseGPT, Wanda) both with and without the Adaptive Layer Sparsity (ALS) technique. This allows for a direct comparison of the effectiveness of ALS in improving the performance of sparse LLMs.

This table presents the average accuracy across seven zero-shot tasks for various LLMs (LLaMA-V1, LLaMA-V2, LLaMA-V3, and OPT) at a 50% sparsity level. It compares the performance of different pruning methods (Dense, Magnitude, Magnitude w. ALS, SparseGPT, SparseGPT w. ALS, Wanda, and Wanda w. ALS). The results show the impact of the Adaptive Layer Sparsity (ALS) method on improving the accuracy of sparse LLMs.
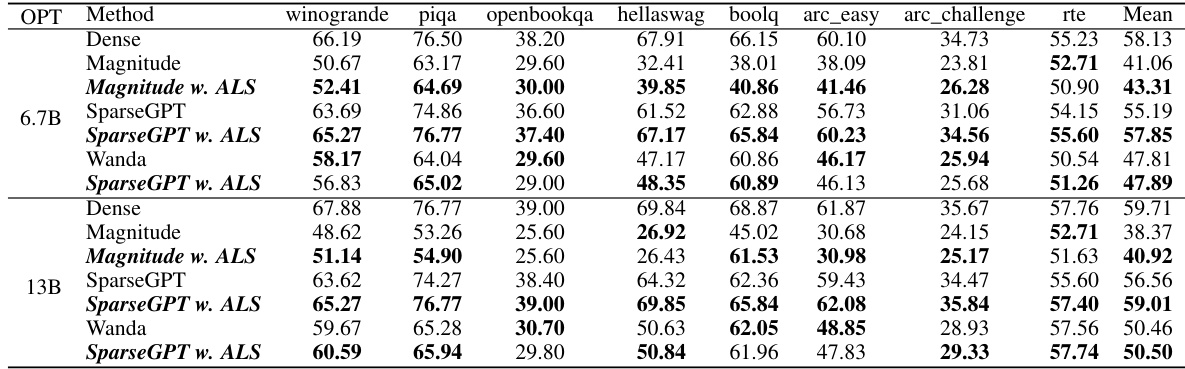
This table presents the WikiText-2 perplexity results for several large language models (LLMs) at a 50% sparsity rate. Different pruning methods (Magnitude, SparseGPT, Wanda) were used, and the results both with and without the Adaptive Layer Sparsity (ALS) method are shown. This allows for a comparison of the effectiveness of ALS across different LLMs and base pruning techniques.
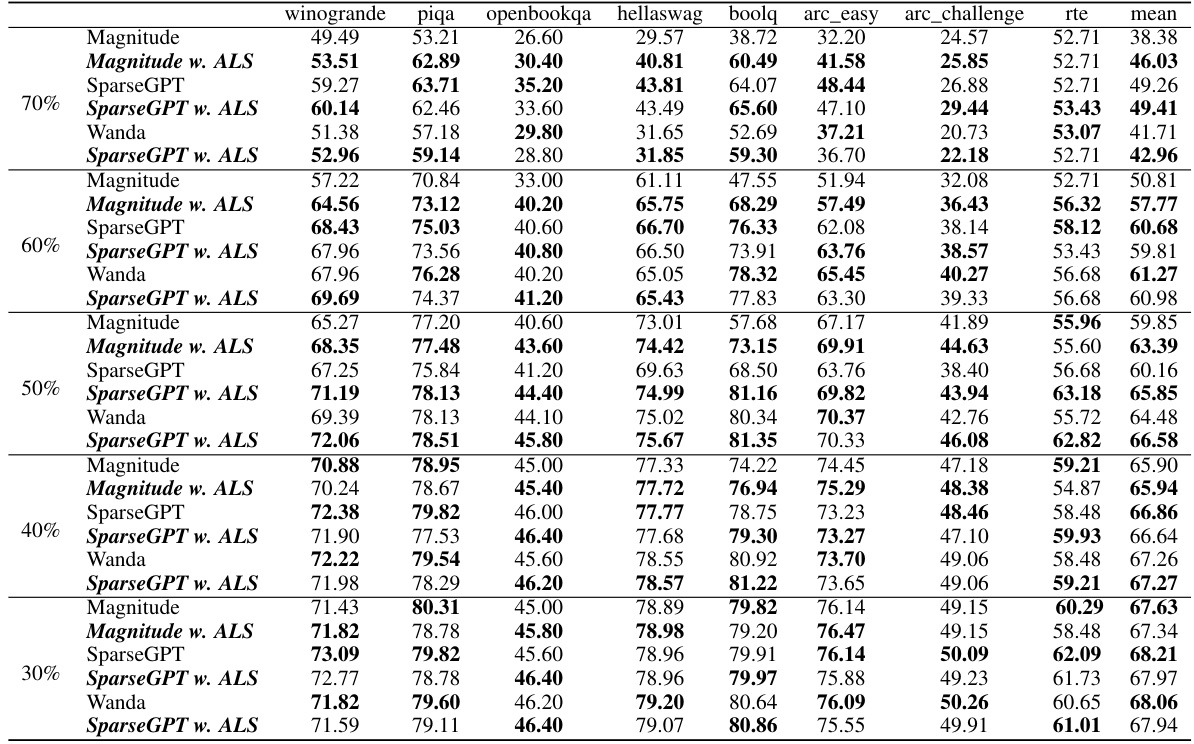
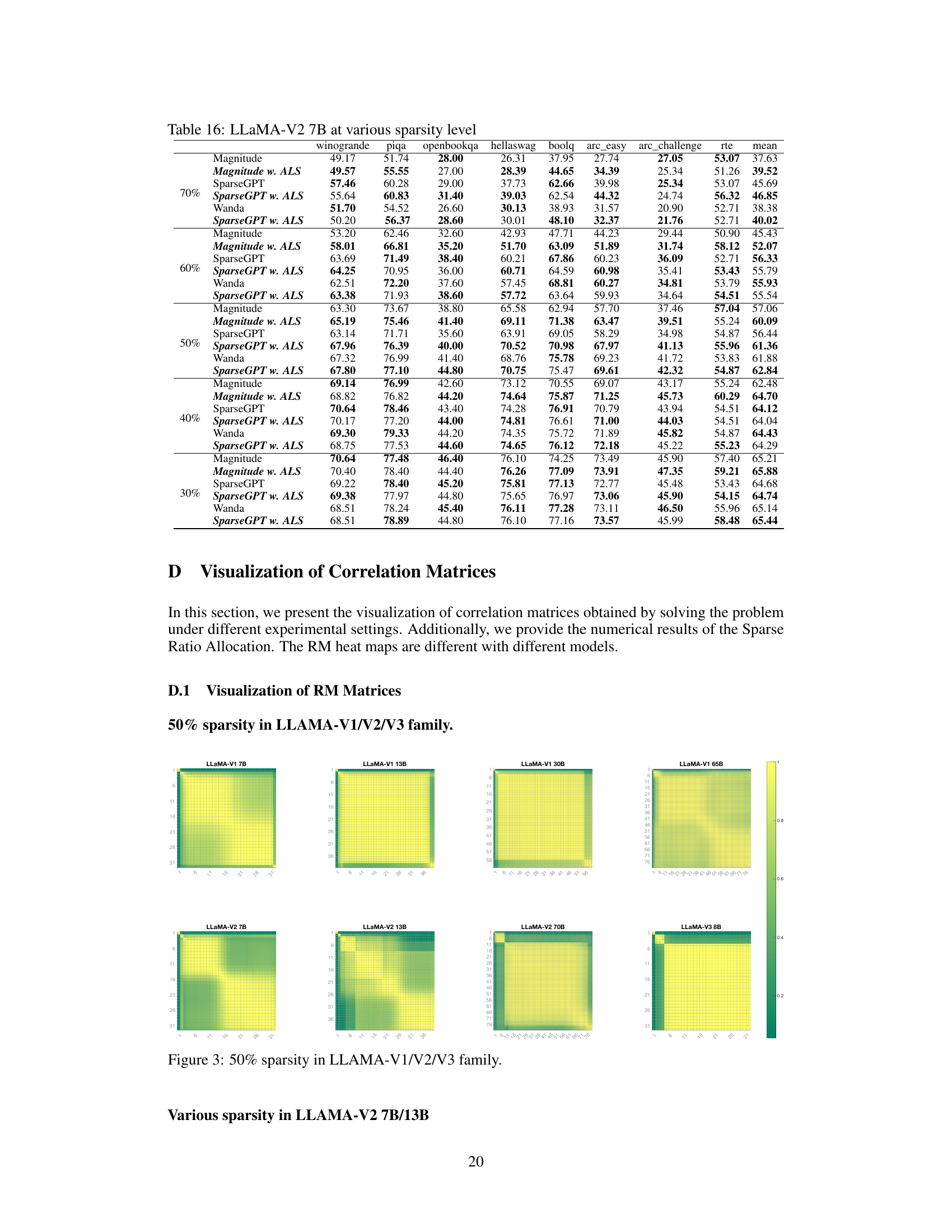
This table presents the WikiText-2 perplexity results for the LLaMA-V2 7B and 13B models at various sparsity levels (20% to 70%). It compares the performance of ALS against three baseline methods (Magnitude, SparseGPT, and Wanda) both with and without the ALS method applied. The table shows how the perplexity changes across different sparsity levels and methods, demonstrating ALS’s effectiveness in maintaining performance even with high sparsity.
This table presents the WikiText-2 perplexity scores achieved by applying Adaptive Layer Sparsity (ALS) to the LLaMA-V2 7B and 13B models which were previously pruned using three different methods: Magnitude, SparseGPT, and Wanda. The table shows the perplexity at varying sparsity levels (20%, 30%, 40%, 50%, 60%, 70%). For each sparsity level and pruning method, the table presents the perplexity before and after applying ALS, demonstrating the effectiveness of ALS in improving the performance of sparse LLMs.

This table presents the WikiText-2 perplexity scores achieved by the Adaptive Layer Sparsity (ALS) method at different sparsity levels (20% to 70%) when applied to the LLaMA-V2 7B and 13B models. For comparison, the perplexity results using three other methods (Magnitude, SparseGPT, and Wanda) are also shown, both with and without ALS. The table highlights the effectiveness of ALS in maintaining low perplexity even at high sparsity levels.
Full paper#