↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Over-parameterized neural networks trained with gradient descent often exhibit excellent generalization. However, understanding gradient descent’s implicit bias towards adversarial robustness remains a challenge. Existing research often overlooks the architectural aspects, focusing primarily on two-layer models. This limits the generalizability of findings to more complex deep learning architectures.
This paper addresses this gap by exploring whether neural network layers collaborate to enhance adversarial robustness during training. The researchers introduce ‘co-correlation’ to quantify inter-layer collaboration, demonstrating a monotonically increasing trend, implying a decreasing trend in robustness during gradient descent. They also observe differing behaviours between narrow and wide networks. Extensive experiments validate their findings, providing a more nuanced understanding of the implicit bias and its influence on model robustness.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on adversarial robustness and generalization in neural networks. It provides a novel theoretical framework for understanding the implicit bias of gradient descent, offering insights into the complex interplay between layers and their impact on model performance. The findings challenge existing assumptions and open avenues for improving adversarial robustness in deep learning models. This research is highly relevant to current trends in AI safety and trustworthiness, contributing significantly to the development of more reliable and secure machine learning systems.
Visual Insights#
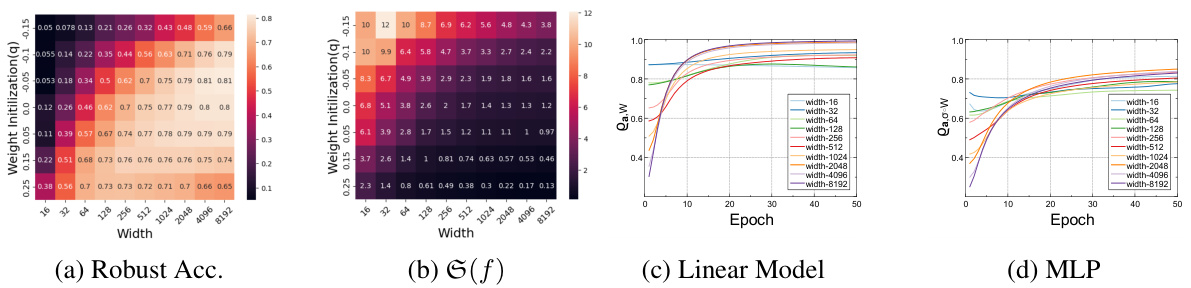
This figure displays the relationship between Dirichlet energy, robust accuracy, and co-correlation dynamics for various MLPs. Panel (a) shows that lower Dirichlet energy correlates with higher robust accuracy. Panel (b) shows Dirichlet energy values for different MLPs. Panels (c) and (d) show the dynamic changes in co-correlation over epochs for linear models and MLPs respectively, demonstrating a general trend of increasing co-correlation during gradient descent. The weight initialization parameter ‘q’ is set to 0.25, as defined in Assumption 5.1 of the paper.
In-depth insights#
Implicit Bias Dynamics#
Analyzing implicit bias dynamics in the context of deep learning reveals crucial insights into model behavior. Gradient descent’s implicit bias, often favoring solutions with good generalization, interacts complexly with the architecture and optimization process. This interaction shapes the model’s susceptibility to adversarial attacks, highlighting the trade-off between generalization and robustness. Understanding how these dynamics evolve during training, possibly through metrics like co-correlation between layers, could allow for better control over model properties, leading to the development of more robust and reliable AI systems. Further research should investigate diverse network architectures to determine the extent to which these dynamics are universal or architecture-specific. Weight initialization strategies may further influence these dynamics, providing another avenue for exploration in shaping implicit bias. The interplay between these factors underscores the need for a deeper understanding to improve the reliability of machine learning.
Layer Collaboration#
The concept of ‘Layer Collaboration’ in the context of deep learning, as explored in the research paper, centers on how individual layers of a neural network interact and influence each other’s behavior, particularly concerning adversarial robustness. The paper introduces the novel metric ‘co-correlation’ to quantify this interaction. High co-correlation indicates strong alignment in feature selection between layers, suggesting a potential trade-off: while improving generalization, it might hinder adversarial robustness. The dynamic analysis reveals a monotonically increasing trend in co-correlation during training, implying a decreasing trend in robustness. Furthermore, the study reveals interesting differences in the behavior of narrow versus wide neural networks, with wider networks exhibiting more robustness and less susceptibility to the negative effects of high co-correlation.
Dirichlet Energy Metric#
The concept of using Dirichlet energy as a metric for adversarial robustness in neural networks is novel and promising. It offers a theoretical framework for understanding the relationship between the variability of a network’s output and its vulnerability to adversarial attacks. By linking Dirichlet energy to the Jacobian matrix of the network mapping, the authors provide a way to quantify adversarial risk and potentially identify the contributions of individual layers to overall robustness. A key strength lies in its extension beyond Lipschitz continuity, offering a more nuanced and potentially more effective measure. However, further investigation is needed to fully explore its practical implications. The computational cost of calculating Dirichlet energy for large networks could be significant. Furthermore, the relationship between Dirichlet energy and adversarial robustness needs thorough empirical validation across diverse architectures and datasets. Despite these challenges, the Dirichlet energy metric presents a valuable theoretical contribution, potentially leading to more principled defenses against adversarial examples.
Network Width Effects#
The study reveals that network width significantly impacts the dynamics of co-correlation and adversarial robustness during gradient descent. Narrow networks exhibit a strong tendency towards increased co-correlation between layers, which conversely weakens adversarial robustness. This effect is primarily attributed to the interplay between the weight initialization and the optimization process. Wider networks, on the other hand, exhibit more resistance to this co-correlation increase, maintaining better adversarial robustness, even with increased training epochs. Weight initialization plays a critical role, particularly in narrow networks, showing that specific initializations can either amplify or mitigate the negative consequences of high co-correlation. This finding challenges the common assumption that wider networks are inherently more robust, revealing the crucial interplay between architecture and optimization strategies in determining a network’s overall robustness.
Future Research#
Future research directions stemming from this work could explore extending the theoretical analysis to deeper, more complex network architectures, moving beyond the two-layer MLPs examined here. Investigating the interaction between layers in convolutional neural networks (CNNs) and recurrent neural networks (RNNs) would be particularly valuable given their prevalence in modern AI. Another crucial area is robustness to different types of adversarial attacks, going beyond the L2 norm attacks used in this study to encompass other adversarial perturbation methods. It would be valuable to explore how the interplay between collaboration and adversarial robustness changes with different activation functions and training algorithms. Finally, empirical investigations of how network width affects generalization performance and adversarial robustness in the context of cross-layer collaboration would yield valuable insights and help refine the theoretical findings presented here.
More visual insights#
More on figures

This figure shows the dynamics of co-correlation for ResNet50 and WRN50 networks trained on CIFAR10. Different partitioning strategies are used (A1-A2 and B1-B2, illustrated in 2a), separating the head and tail parts of the networks, to analyze the impact of different network sections on the co-correlation. The plots (2b and 2c) display the co-correlation change over training epochs for each partition strategy, highlighting the differences in the dynamics between the two network architectures.

This figure shows how the co-correlation changes over epochs for MLP networks with different widths (32, 512, 2048, and 8192) and various weight initializations (q = -0.15, -0.1, -0.05, 0, 0.05, 0.1, 0.15, 0.25). Each subplot represents a different network width. The x-axis represents the number of epochs during training, and the y-axis shows the value of the co-correlation. The different colored lines within each subplot represent the various weight initializations. This figure illustrates the impact of network width and weight initialization on the dynamics of co-correlation during gradient descent.
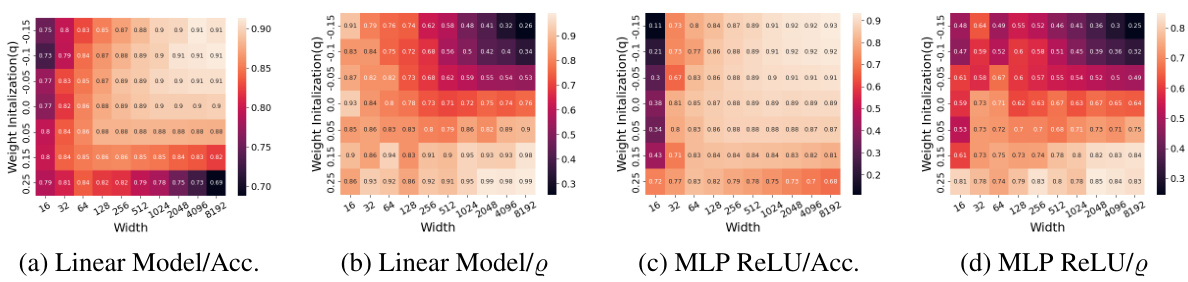
This figure displays the accuracy and co-correlation for both linear and MLP models as heatmaps. Each cell in the heatmap represents a trained network. The heatmaps visualize the relationship between accuracy, co-correlation, network width, and weight initialization (q) for both linear models and MLPs with ReLU activation function. It shows how these factors influence the performance and robustness of the models.
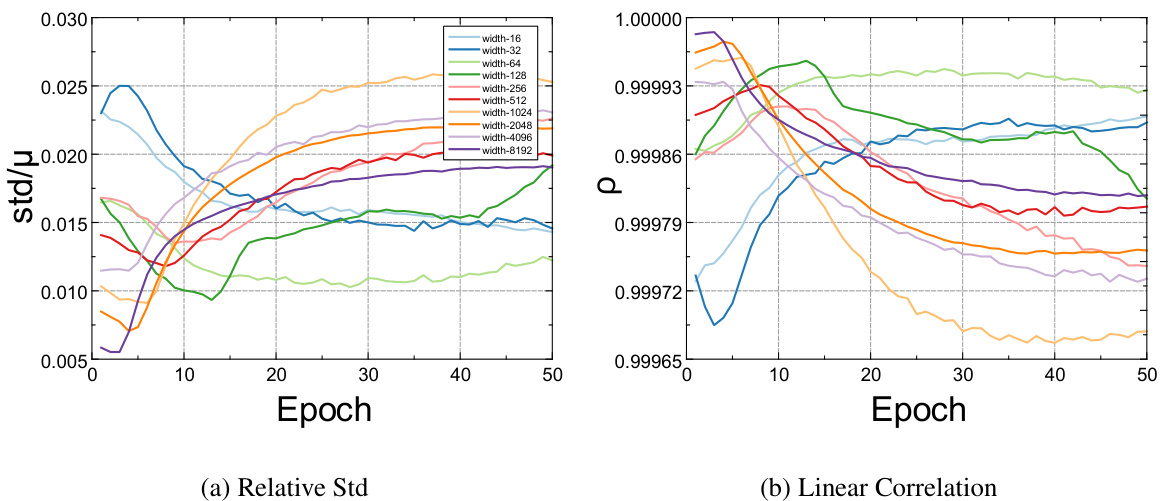
Figure 5 presents two sub-figures. The left sub-figure (a) shows the relative standard deviation of the L2-norm of the Jacobian over its mean for various MLPs with different widths. The right sub-figure (b) displays the linear correlation between the L2-norms of Jacobians for adjacent layers of these MLPs. Both sub-figures illustrate the dynamics across 50 training epochs, with the initialization parameter q set to 0.25 for all MLPs. The plots provide insights into the stability and correlation of feature selection across layers during training.
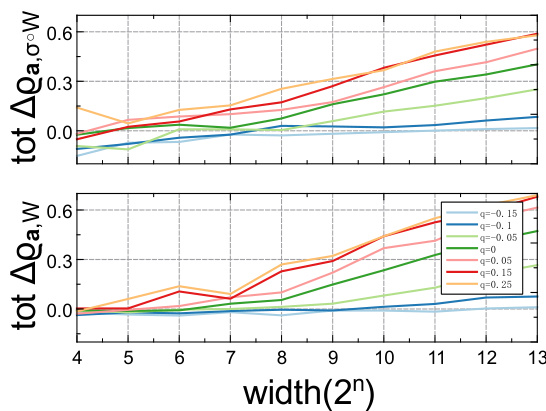
This figure shows how co-correlation accumulates during training in neural networks with different widths and weight initializations. The x-axis represents the width (2n), while different colored lines represent different weight initialization settings (q). The top plot shows results for a ReLU model, while the bottom plot shows results for a linear model. The figure demonstrates the relationship between network width, weight initialization, and the accumulation of co-correlation.
Full paper#



















