↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Existing methods for domain-specific continual pre-training (D-CPT) in large language models (LLMs) rely on laborious, computationally expensive grid-searching for optimal data mixture ratios. This paper addresses this limitation. The research highlights the challenges of selecting optimal mixture ratios between general and domain-specific corpora in D-CPT for LLMs. These ratios significantly impact the model’s performance and existing methods are inefficient and costly.
To overcome these challenges, the authors propose the D-CPT Law, a novel scaling law inspired by previous Scaling Laws. The D-CPT Law accurately predicts performance using small-scale training, significantly reducing computational costs. It also introduces the Cross-Domain D-CPT Law, allowing efficient prediction for new domains with minimal training. The effectiveness and generalizability of both laws are demonstrated across various downstream tasks, showcasing their utility in optimizing LLM training and resource allocation.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with large language models (LLMs) and continual pre-training (CPT). It introduces a novel Scaling Law, the D-CPT Law, which enables efficient prediction of optimal training parameters, significantly reducing computational costs. Further, the Cross-Domain D-CPT Law extends this efficiency to new domains, opening avenues for faster, more cost-effective LLM adaptation and domain-specific model development.
Visual Insights#

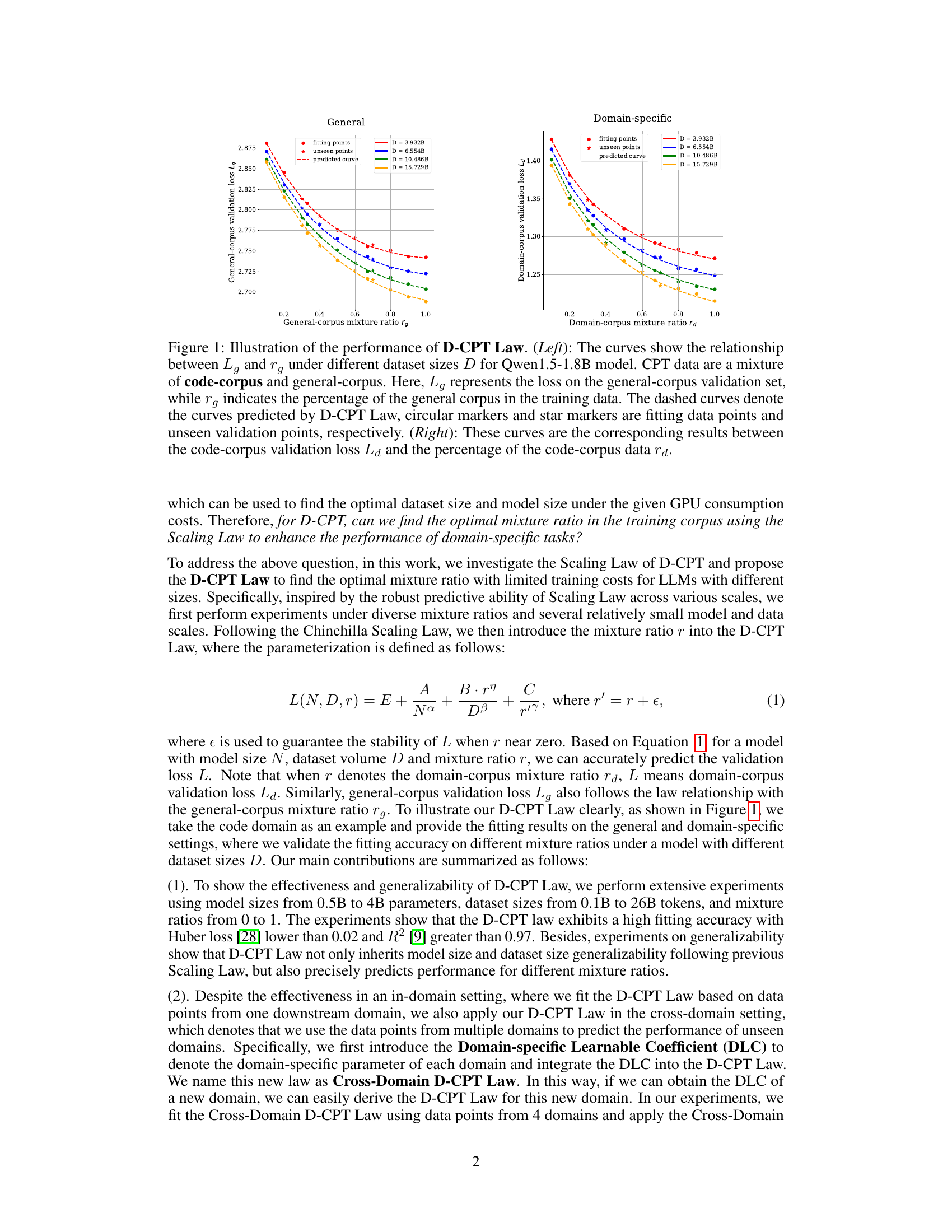
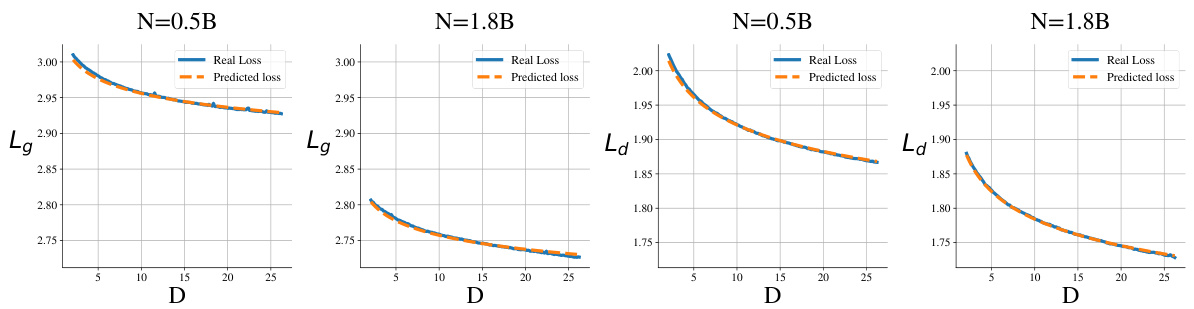
This figure shows the performance of the D-CPT Law. The left panel shows the relationship between the general corpus validation loss (Lg) and the general corpus mixture ratio (rg) for different dataset sizes. The right panel shows the same relationship but for the domain-specific corpus validation loss (Ld) and domain-specific corpus mixture ratio (rd). The dashed lines represent the predicted values from the D-CPT Law, showing its ability to accurately predict performance for unseen mixture ratios. Circular markers are fitting points, while star markers are unseen validation points.

This table presents the performance comparison of five different parameterizations of the D-CPT Law across six domains (general and five domain-specific ones). The performance is measured using Huber loss (lower is better) and R-squared (higher is better) for both the general and domain-specific datasets. The number of fitting parameters for each parameterization is also listed. Appendix J contains more detailed results for each domain.
In-depth insights#
D-CPT Law Unveiled#
The hypothetical ‘D-CPT Law Unveiled’ section likely presents a novel scaling law for domain-specific continual pre-training (D-CPT) in large language models (LLMs). This law would quantify the relationship between model performance, dataset size, model size, and the mixture ratio of general and domain-specific data used during training. The core contribution would be a mathematical formula enabling researchers to predict optimal mixture ratios for D-CPT, eliminating the need for expensive and time-consuming grid searches. Furthermore, an extension to a ‘Cross-Domain D-CPT Law’ is likely proposed, allowing for efficient performance prediction in new domains using limited training data, potentially by introducing a domain-specific learnable coefficient. The research is significant as it streamlines D-CPT, reducing resource consumption and enhancing the efficiency of LLM adaptation to specialized domains. Experimental validation across multiple datasets and model sizes would be crucial for demonstrating the law’s generalizability and robustness.
Cross-Domain Scaling#
Cross-domain scaling in large language models (LLMs) addresses the challenge of transferring knowledge learned in one domain to improve performance in another, related domain. This is crucial because training LLMs from scratch for every new domain is computationally expensive and data-intensive. Effective cross-domain scaling methods leverage pre-trained models, which have already learned general linguistic representations, and adapt them to the target domain using less data and computation. This is often achieved through techniques like transfer learning, domain adaptation, or multi-task learning. A key consideration is the relatedness between source and target domains: the more similar they are, the easier the transfer. Measuring the effectiveness of cross-domain scaling involves comparing performance on the target domain after transfer to the performance achieved by training a model specifically for that domain. Successful cross-domain scaling not only reduces computational costs but also improves generalization capabilities of LLMs by allowing them to leverage knowledge acquired in one domain to enhance performance in other, related domains.
Mixture Ratio’s Role#
The optimal mixture ratio between general and domain-specific corpora in continual pre-training is crucial for large language models (LLMs). A balanced ratio is key to preventing catastrophic forgetting, where the model loses previously acquired knowledge, while simultaneously improving performance on the target domain. Finding this optimum often involves laborious grid searches, consuming significant computational resources. This paper proposes a scaling law approach—the D-CPT Law—to predict optimal ratios for diverse model and dataset sizes, drastically reducing the computational burden. The D-CPT Law leverages a mathematical formulation to predict performance across various ratios, enabling efficient exploration and selection of the most effective mixture without extensive training. Moreover, an extension—the Cross-Domain D-CPT Law—allows for prediction in new domains using a small amount of data, further enhancing efficiency and generalizability. The method’s effectiveness is demonstrated across multiple domains, highlighting its potential for efficient and effective continual pre-training of LLMs.
D-CPT Law’s Limits#
The D-CPT Law, while innovative in predicting optimal training parameters for domain-specific continual pre-training, faces limitations. Its reliance on small-scale initial experiments to extrapolate to large-scale training is a major constraint. The accuracy of predictions hinges heavily on the representativeness of these initial experiments, and the generalizability across different model architectures and domain types needs further validation. The computational costs, although reduced, remain significant, limiting broader accessibility. Furthermore, the law’s performance is highly sensitive to parameter initialization, requiring robust optimization strategies. The impact of data characteristics, beyond size, on the accuracy of the predictions requires deeper investigation. The introduction of the Cross-Domain D-CPT Law attempts to mitigate some limitations but introduces additional complexities in parameter estimation and potentially reduces accuracy. Lastly, the applicability to multilingual settings has not been fully explored and requires further research. Addressing these limitations is crucial to the widespread adoption and impact of the D-CPT Law.
Future Research#
Future research directions stemming from this D-CPT Law study could explore its application to a wider array of domains and LLMs. Extending the model’s multilingual capabilities is crucial, given the current limitations. Investigating alternative fitting algorithms and methods to reduce reliance on initial parameterizations would enhance robustness. Further research into improving the efficiency of Scaling Law, thereby reducing computational costs, is also highly desirable. A particularly promising area lies in refining the identification of the inflection point (ri) in the relationship between the mixture ratio and dataset size, as this would significantly enhance predictive accuracy for small mixture ratios. Finally, exploring the interplay between the D-CPT Law and other scaling laws, such as those for compute, could provide a more holistic understanding of large language model training dynamics.
More visual insights#
More on figures
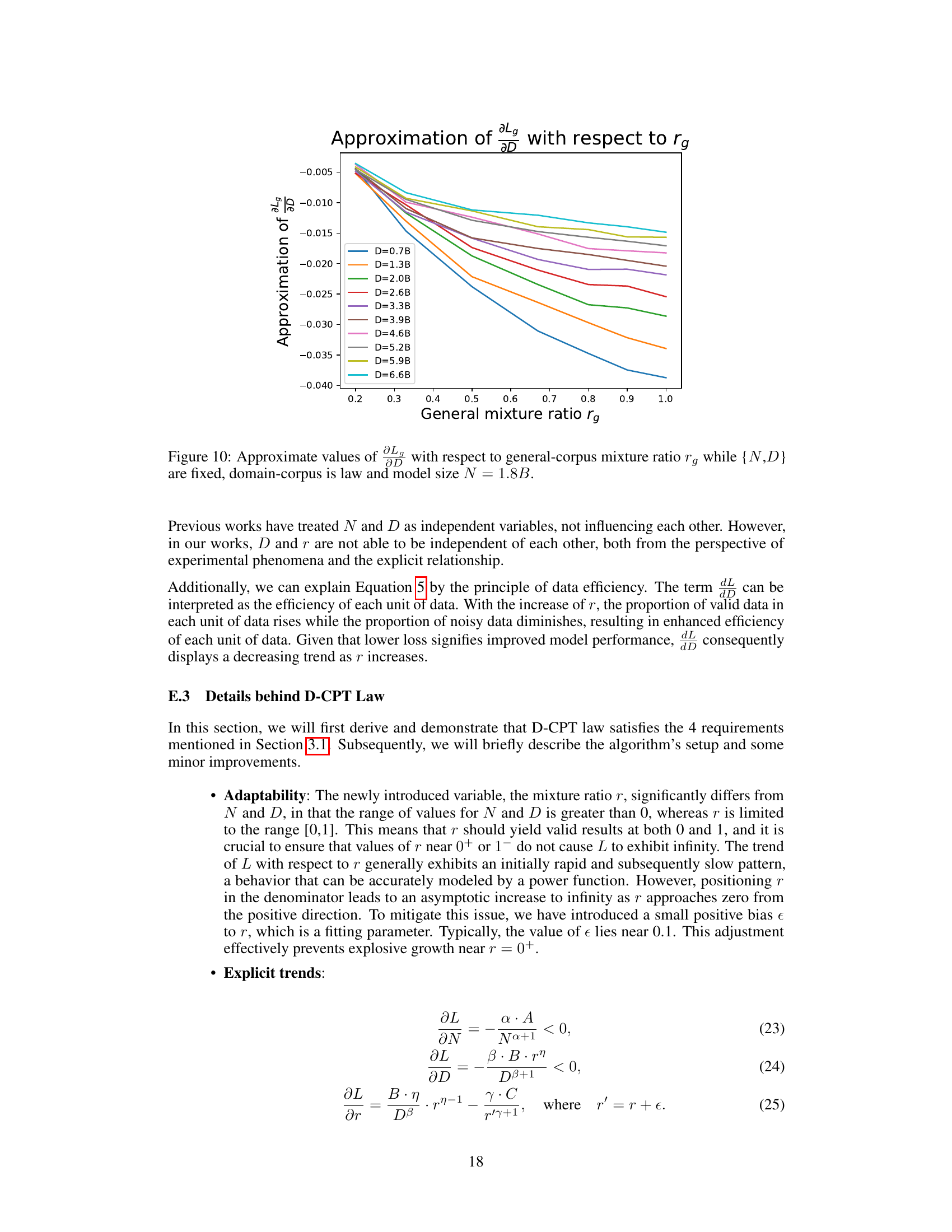
This figure illustrates the workflow of the proposed D-CPT Law and Cross-Domain D-CPT Law. The upper part shows the in-domain setting where data from multiple domains are used to train a small-scale model and fit the D-CPT law. This allows prediction of model performance at larger scales. The lower part depicts the cross-domain setting. The domain-specific learnable coefficient (DLC) is calculated for an unseen domain (e.g., Physics), integrated into the cross-domain D-CPT law, and then used to predict the performance in that domain. Three applications are highlighted: optimal mixture ratio for balancing general and domain-specific abilities, optimal mixture for limited domain data, and resource allocation.
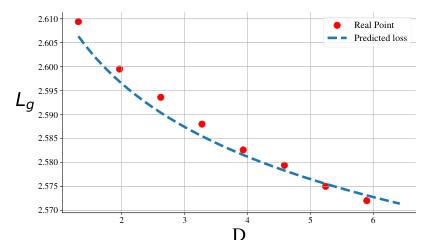
This figure demonstrates the effectiveness of the proposed D-CPT Law in predicting the performance of continual pre-training models with different dataset sizes, model sizes, and mixture ratios of general and domain-specific corpora. The left panel shows the relationship between general corpus validation loss and the proportion of general corpus in training data, while the right panel shows the same relationship for the domain-specific corpus.
This figure demonstrates the effectiveness of the D-CPT Law in predicting the performance of continual pre-training with varying mixture ratios of general and domain-specific corpora. The left panel shows the relationship between the general corpus validation loss and the percentage of general corpus in the training data for different dataset sizes, while the right panel shows the same for domain-specific corpus validation loss. The dashed lines represent predictions from the D-CPT Law, showing its accuracy in capturing the relationship between the loss and mixture ratio across various model sizes and dataset sizes.
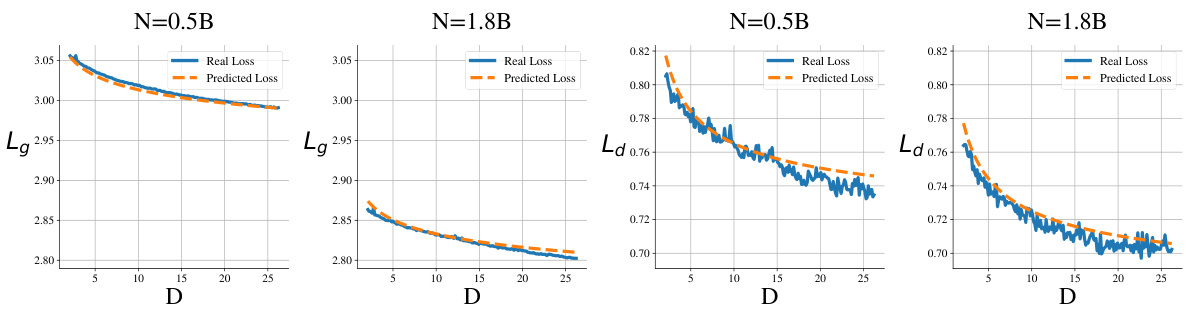
The figure illustrates the performance of the proposed D-CPT Law. The left panel shows the relationship between the general-corpus validation loss (Lg) and the general-corpus mixture ratio (rg) under various dataset sizes. The right panel shows the analogous relationship between code-corpus validation loss (La) and the code-corpus mixture ratio (rd). Dashed lines represent the predictions made by the D-CPT Law, while markers represent actual training data and unseen validation data.

This figure shows the performance of the proposed D-CPT Law in predicting the validation loss (Lg and La) on general and domain-specific corpora, respectively, under different dataset sizes (D) and mixture ratios (rg and rd) using the Qwen1.5-1.8B model. The left panel shows the relationship between the general corpus validation loss and the percentage of general corpus in the training data. The right panel shows the relationship between the domain-specific corpus validation loss and the percentage of domain-specific corpus in the training data. Dashed lines represent predictions from the D-CPT Law, while circular and star markers represent fitting and unseen validation data, respectively.

This figure demonstrates the effectiveness of the D-CPT Law in predicting the performance of continual pre-training (CPT) on large language models (LLMs). The left panel shows the relationship between general-corpus validation loss (Lg) and the proportion of general-corpus data (rg) for various dataset sizes. The right panel shows a similar relationship between code-corpus validation loss (La) and the proportion of code-corpus data (ra). Dashed lines represent the D-CPT Law predictions, while markers show the actual training results. The close fit between predicted and actual values demonstrates the accuracy of the D-CPT Law.
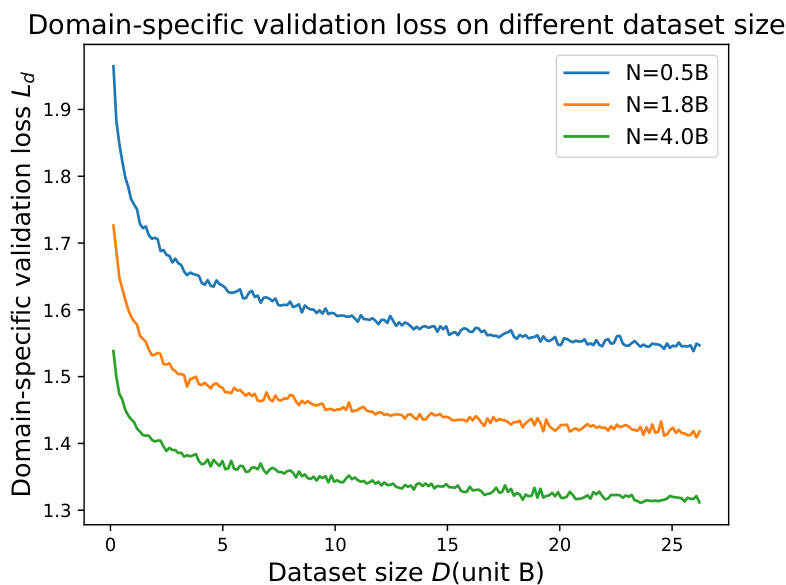
The figure demonstrates the performance of the proposed D-CPT Law for predicting the optimal mixture ratio in continual pre-training of large language models. The left panel shows the relationship between the general corpus validation loss (Lg) and the general corpus mixture ratio (rg) for different dataset sizes, while the right panel shows the corresponding relationship for the domain-specific corpus. The dashed lines represent the predictions of the D-CPT Law, which accurately predicts performance with small-scale training costs.
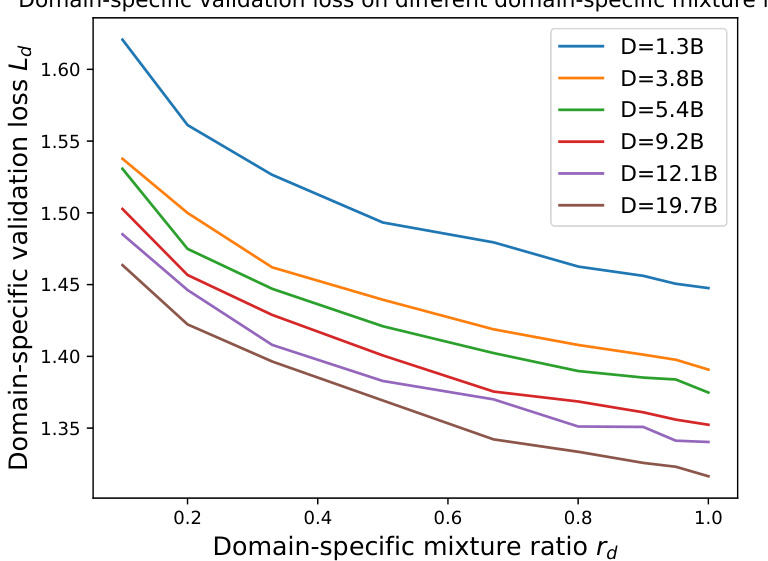
This figure shows the performance of the proposed Domain-specific Continual Pre-Training Scaling Law (D-CPT Law). The left panel shows the relationship between the general corpus validation loss (Lg) and the general corpus mixture ratio (rg) for different dataset sizes. The right panel shows the same relationship but for the domain-specific corpus validation loss (La) and the domain-specific corpus mixture ratio (rd). Dashed lines represent the predictions of the D-CPT Law, demonstrating its accuracy in predicting model performance under various dataset sizes and mixture ratios.

This figure shows the performance of the proposed Domain-specific Continual Pre-Training Scaling Law (D-CPT Law). The left panel shows the relationship between the general corpus validation loss (Lg) and the general corpus mixture ratio (rg) for different dataset sizes. The right panel shows a similar relationship but for the domain-specific corpus validation loss (La) and the domain-specific corpus mixture ratio (rd). Dashed lines represent predictions from the D-CPT Law, while markers show actual training and validation results.

This figure demonstrates the performance of the proposed Domain-specific Continual Pre-training Scaling Law (D-CPT Law). The left panel shows the relationship between the general corpus validation loss (Lg) and the percentage of general corpus in the training data (rg) for different dataset sizes. The right panel shows the corresponding relationship between the domain-specific corpus validation loss (La) and the percentage of domain-specific corpus in the training data (rd). Dashed lines represent the D-CPT Law predictions, while markers show the actual training data.

This figure demonstrates the effectiveness of the D-CPT Law in predicting the performance of continual pre-training on large language models. The left panel shows the relationship between the general corpus validation loss (Lg) and the general corpus mixture ratio (rg) for various dataset sizes. The right panel shows the same relationship between code corpus validation loss (La) and the code corpus mixture ratio (ra). The dashed lines are predictions from the D-CPT Law, which closely match the observed data points.
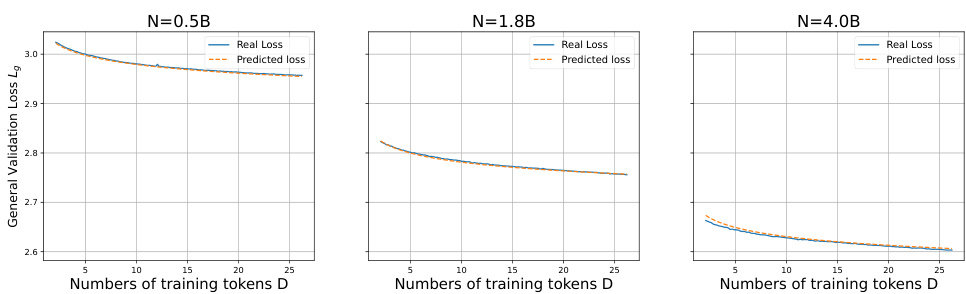
This figure shows the performance of the proposed D-CPT Law by plotting the general-corpus validation loss (Lg) against the general-corpus mixture ratio (rg) and the domain-specific validation loss (La) against the domain-corpus mixture ratio (rd) for different model sizes. The dashed lines represent the predicted values by the D-CPT Law, while the markers represent the actual experimental results. This visualization demonstrates how well the D-CPT Law can predict the performance for various model and data scales.

This figure shows the performance of the D-CPT Law in predicting the optimal mixture ratio for continual pre-training. The left panel shows the relationship between the general corpus validation loss (Lg) and the percentage of general corpus in the training data (rg) for different dataset sizes. The right panel shows the corresponding relationship between the domain-specific (code) corpus validation loss (La) and the percentage of domain-specific corpus (rd). The dashed lines represent the predictions from the D-CPT Law, demonstrating its accuracy in predicting performance across various conditions.
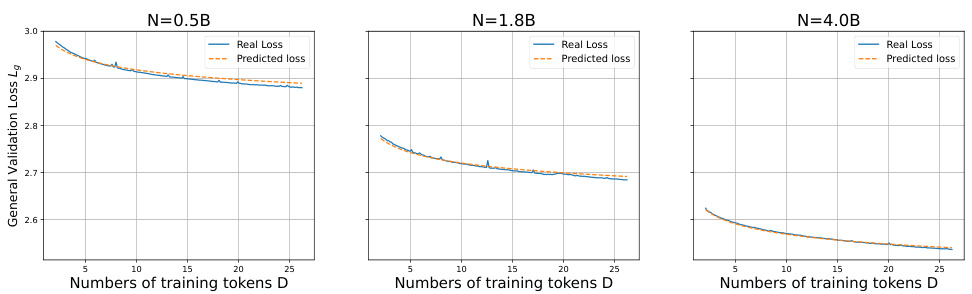
This figure shows the performance of the proposed D-CPT Law in predicting the validation loss (Lg and La) on general and code-specific corpora, respectively, for different model sizes, dataset sizes, and mixture ratios of the training data. The left panel illustrates the relationship between the general-corpus validation loss and the percentage of general corpus in the training data, and the right panel shows a similar relationship for the code-corpus validation loss. The dashed lines represent the predictions of the D-CPT Law, and the markers show the actual data points (fitting and unseen). The results demonstrate that the D-CPT Law accurately predicts the performance under various conditions.

This figure shows the performance of the D-CPT Law in predicting the optimal mixture ratio for continual pre-training of large language models. The left panel shows the relationship between the general corpus validation loss (Lg) and the proportion of general corpus in the training data (rg) for different dataset sizes. The right panel shows the corresponding relationship between the domain-specific corpus validation loss (La) and the proportion of domain-specific corpus (rd). The dashed lines represent the D-CPT Law’s predictions, while the markers show the actual training results. The figure demonstrates the D-CPT Law’s ability to accurately predict performance across different mixture ratios and dataset sizes.

The figure illustrates the performance of the proposed Domain-specific Continual Pre-Training Scaling Law (D-CPT Law). The left panel shows the relationship between the general corpus validation loss (Lg) and the proportion of general corpus data (rg) in the training data, for different dataset sizes. The right panel shows the corresponding relationship for the code-specific validation loss (La) and the proportion of code corpus data (rd). Dashed lines represent the predictions made by the D-CPT Law, demonstrating its accuracy in predicting performance based on small-scale experiments.
More on tables

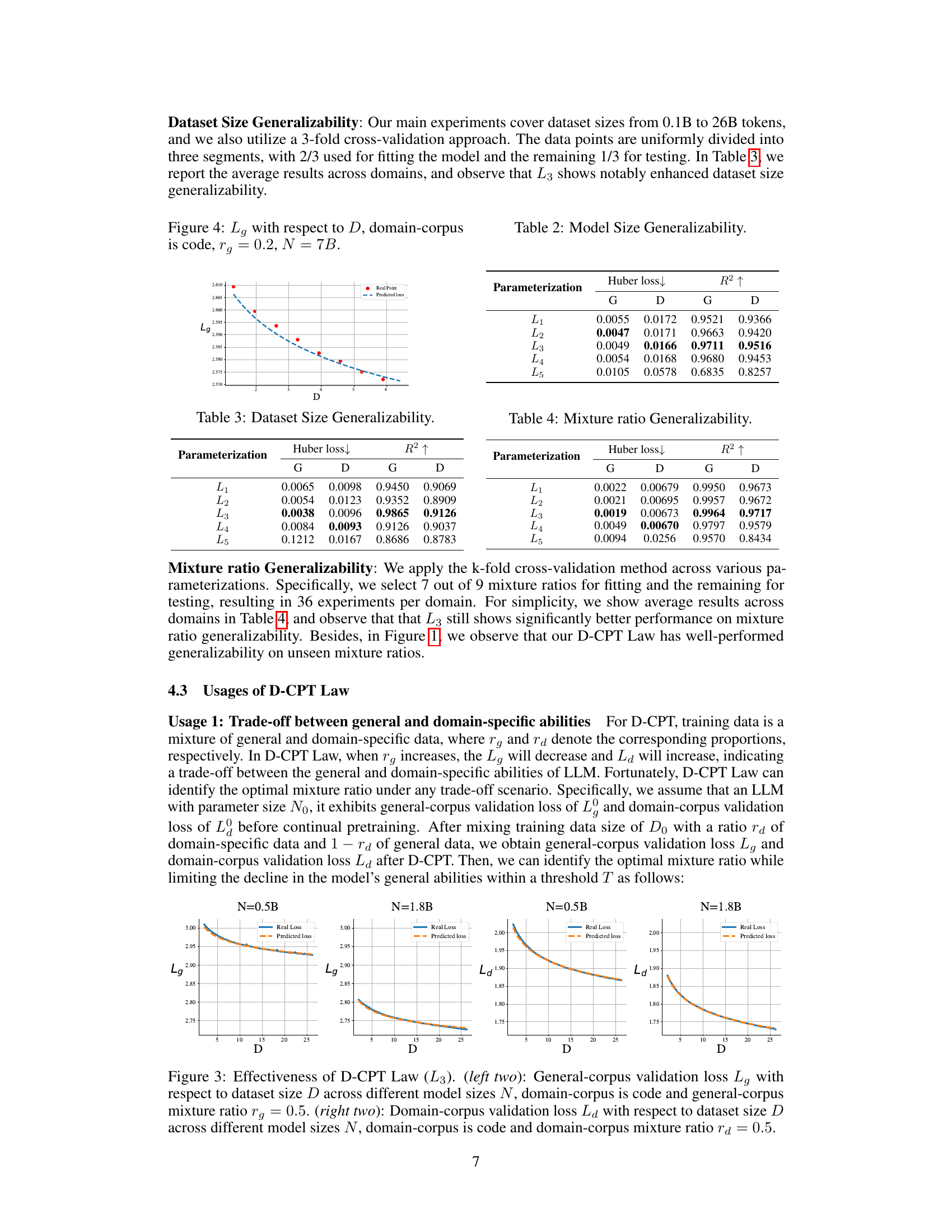
This table presents the results of a 3-fold cross-validation experiment to evaluate the model size generalizability of the D-CPT Law. It shows the Huber loss and R-squared values for the general and domain-specific corpora across different model sizes (0.5B, 1.8B, and 4B parameters) and across different parameterizations of the D-CPT Law (L1-L5). Lower Huber loss and higher R-squared values indicate better generalizability.

This table presents the Huber loss and R-squared values for five different parameterizations of the D-CPT Law across six domains (general and five downstream domains). Lower Huber loss and higher R-squared indicate better model performance. The table shows the average performance across all domains, with more detailed results available in Appendix J.
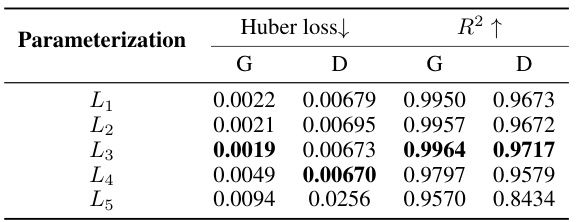
This table presents the results of mixture ratio generalizability experiments. It compares five different parameterizations (L1-L5) of the D-CPT Law across six domains (general and five downstream domains). For each parameterization and domain, it shows the Huber loss and R-squared values, indicating the quality of the model’s fit to the experimental data points at different mixture ratios. Lower Huber loss and higher R-squared values signify better model performance and generalizability.

This table shows the real general-corpus validation loss (Lg) and domain-corpus validation loss (Ld) for different domain-corpus mixture ratios (rd). The highlighted row indicates the optimal mixture ratio (rd = 0.924) that minimizes the domain-specific loss while keeping the general loss within an acceptable threshold (3% increase from the initial general loss). This demonstrates the effectiveness of the D-CPT Law in identifying the optimal ratio for a desired trade-off between general and domain-specific performance.

This table shows the real domain-corpus validation loss (Ld) for different values of the domain-corpus mixture ratio (rd) when the domain-specific dataset size (Da) is fixed at 5B. It demonstrates the relationship between the mixture ratio and the loss, highlighting the optimal mixture ratio that minimizes the loss.
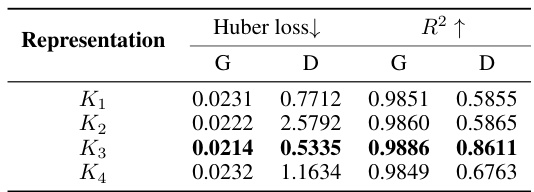
This table shows the performance of four different representations of the Domain-Specific Learnable Coefficient (DLC) in a cross-domain setting. The goal is to determine which representation best predicts the performance of unseen domains using data from only a subset of domains. The table reports Huber loss and R-squared values for both general and domain-specific settings, indicating the accuracy of the prediction. Lower Huber loss and higher R-squared values suggest better performance.
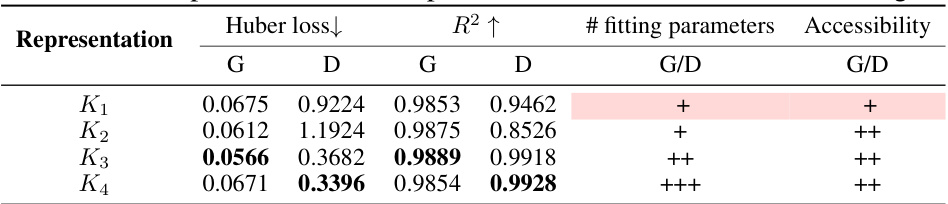
This table presents the performance of four different representations (K1, K2, K3, K4) of the Domain-Specific Learnable Coefficient (DLC) in terms of Huber loss and R-squared values. Lower Huber loss and higher R-squared values indicate better model performance. The table also shows the number of fitting parameters and the accessibility of each representation. The results are used to determine which representation of K is the most suitable for the Cross-Domain D-CPT Law.

This table presents the Huber loss and R-squared values for five different parameterizations of the D-CPT law across six domains (general and five downstream domains). Lower Huber loss and higher R-squared indicate better model performance. The table summarizes the results, with full details in Appendix J.
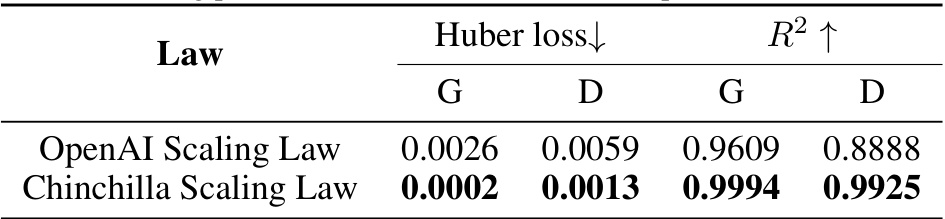
This table compares the fitting performance of two scaling laws, OpenAI Scaling Law and Chinchilla Scaling Law, on a code corpus dataset using a 1:1 mixture ratio. The comparison is based on Huber loss (lower is better) and R-squared (higher is better) values for both general and domain-specific data. The results show that the Chinchilla Scaling Law exhibits significantly better fitting performance than the OpenAI Scaling Law in this specific experimental setup.
This table presents a comparison of five different parameterizations of the D-CPT Law, denoted as L1 through L5. The comparison is based on two key metrics: Huber loss (lower is better) and R-squared (higher is better). The results are shown separately for general domains (G) and downstream domains (D), which represent performance on general language tasks and domain-specific tasks, respectively. The table highlights the best-performing parameterization (L3) based on the lowest Huber loss and the highest R-squared values across both general and downstream domains. The full details for each domain are available in Appendix J.

This table presents the results of five different parameterizations of the D-CPT Law across six downstream domains (Code, Math, Law, Chemistry, Music, Medical). The performance is evaluated using Huber loss and R-squared (R2). ‘G’ represents the general domain, and ‘D’ represents the downstream domains. Lower Huber loss and higher R2 indicate better performance. The table shows the average performance across all six domains, with details for each domain provided in Appendix J. This table is crucial in the paper because it helps to justify the choice of the best parameterization (L3) for the D-CPT Law.
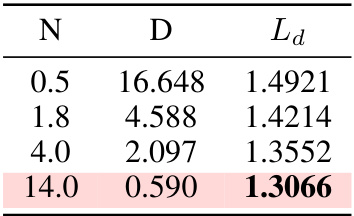
This table presents the results of an experiment where the compute budget was fixed, and the domain-corpus validation loss (Ld) was measured for different model sizes (N) and dataset sizes (D). The results show how the loss changes as the model and dataset sizes are varied while maintaining a constant compute budget. The highlighted row indicates the optimal setting found through the experiment.
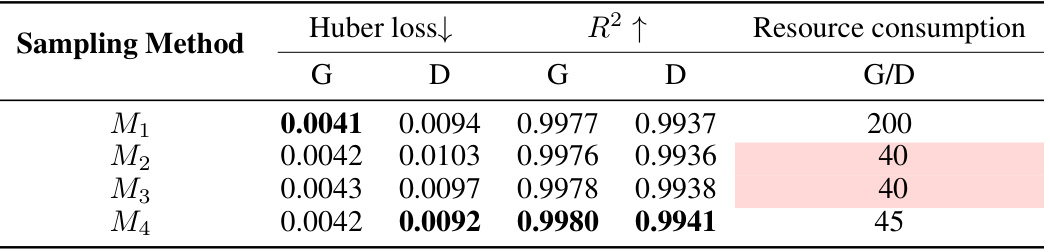
This table compares the performance of four different sampling methods for collecting data points to fit the D-CPT Law. The methods vary in density (dense, sparse, sectional) and use an exponential decay function. The table shows Huber loss, R-squared, and resource consumption (evaluation and storage) for each method, across the general and domain-specific data. Method M4, using an exponential decay function, seems to provide the best balance between accuracy and resource consumption.

This table presents the Huber loss and R-squared values for five different parameterizations of the D-CPT Law across six domains (General, Code, Math, Law, Music, Chemistry, Medical). Lower Huber loss and higher R-squared indicate better fitting performance. The table helps in selecting the best parameterization for the D-CPT Law by comparing their performance across different domains.

This table compares the performance of five different parameterizations of the D-CPT Law across six downstream domains (Code, Math, Law, Music, Chemistry, and Medical). The ‘G’ column represents the performance on the general corpus and the ‘D’ column shows the performance on the domain-specific corpus. It uses Huber loss (lower is better) and R-squared (higher is better) as evaluation metrics. The table highlights the trade-off between fitting performance and the number of parameters used in the models. Appendix J provides more detailed results for each domain.

This table presents the Huber loss, a robust loss function, for five different parameterizations of the D-CPT Law across six domains (Code, Math, Law, Music, Chemistry, Medical). Each value represents the average Huber loss calculated using 3-fold cross-validation, offering a more robust estimate of performance than a single run.

This table presents the average Huber loss and R-squared values across six domains (Code, Math, Law, Music, Chemistry, and Medical) for five different parameterizations (L1-L5) of the D-CPT Law. Lower Huber loss and higher R-squared values indicate better model performance. The ‘G’ and ‘D’ columns represent general and domain-specific metrics, respectively. Appendix J contains detailed results for each domain.

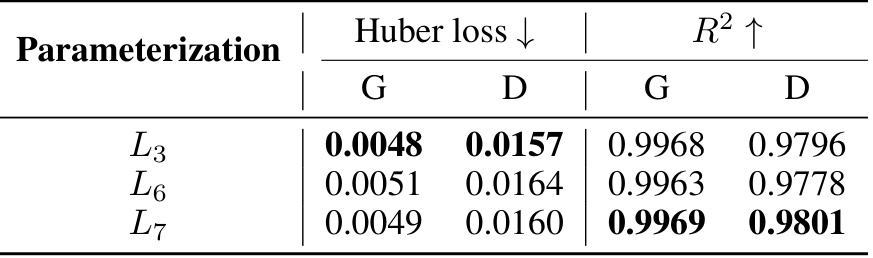
This table compares the performance of three different parameterizations (L3, L6, and L7) of the D-CPT Law across six downstream domains. For each parameterization and domain, it shows the Huber loss and R-squared values for both general and domain-specific validation sets. Lower Huber loss and higher R-squared indicate better performance.

This table compares the performance of three different parameterizations (L3, L6, and L7) of the D-CPT Law across six downstream domains (Code, Math, Law, Music, Chemistry, and Medical). For each parameterization and domain, it shows the Huber loss and R-squared values for both general and domain-specific corpora. Lower Huber loss and higher R-squared indicate better fitting performance.

This table presents a comparison of the performance (Huber loss and R-squared) of three different parameterizations (L3, L6, and L7) of the D-CPT Law across six downstream domains (Code, Math, Law, Music, Chemistry, and Medical). ‘G’ represents the general domain and ‘D’ represents the domain-specific results for each parameterization. The table helps to evaluate which parameterization is most effective by comparing their Huber loss and R-squared values across both general and domain-specific datasets.

This table presents the Huber loss and R-squared values for five different parameterizations of the D-CPT Law across six domains (general and five specific domains). Lower Huber loss and higher R-squared indicate better fitting performance. The table allows comparison of different parameterizations to determine which best fits the D-CPT Law model and provides a summary of performance across various domains. Details for each domain are available in Appendix J.
Full paper#