TL;DR#
Many real-world tasks involve reaching a goal while avoiding unsafe states and minimizing costs. Existing reinforcement learning methods struggle with this ‘minimum-cost reach-avoid’ problem because combining these objectives is challenging. They often use weighted sums of objectives, resulting in suboptimal solutions. This paper tackles the minimum-cost reach-avoid problem by using a novel technique based on Hamilton-Jacobi reachability.
The paper introduces a new algorithm called RC-PPO that addresses the limitations of existing methods. RC-PPO converts the reach-avoid problem into a reachability problem on an augmented system. It uses a two-step process: first learning a policy and value function conditioned on a cost upper bound, and then fine-tuning to find the optimal cost. Experiments show RC-PPO significantly reduces costs compared to existing approaches across various benchmark tasks while maintaining similar success rates. This demonstrates the effectiveness of the proposed method for solving challenging constrained optimization problems.
Key Takeaways#
Why does it matter?#
This paper is important because it presents RC-PPO, a novel reinforcement learning algorithm that efficiently solves the minimum-cost reach-avoid problem, a crucial challenge in many real-world applications. It offers significant cost reduction while maintaining comparable performance to existing methods, opening new avenues for research in constrained optimization and safe reinforcement learning. The detailed analysis and readily available codebase further enhance its value to the research community.
Visual Insights#

🔼 This figure summarizes the two phases of the RC-PPO algorithm. Phase one transforms the original system into an augmented system using RL to optimize the value function and learn a stochastic policy. Phase two fine-tunes the value function on a deterministic policy, calculates the optimal upper bound, and then produces the optimal deterministic policy.
read the caption
Figure 1: Summary of the RC-PPO algorithm. In phase one, the original dynamic system is transformed into the augmented dynamic system defined in (7). Then RL is used to optimize value function V and learn a stochastic policy π. In phase two, we fine-tune V on a deterministic version of π and compute the optimal upper-bound z* to obtain the optimal deterministic policy π*.
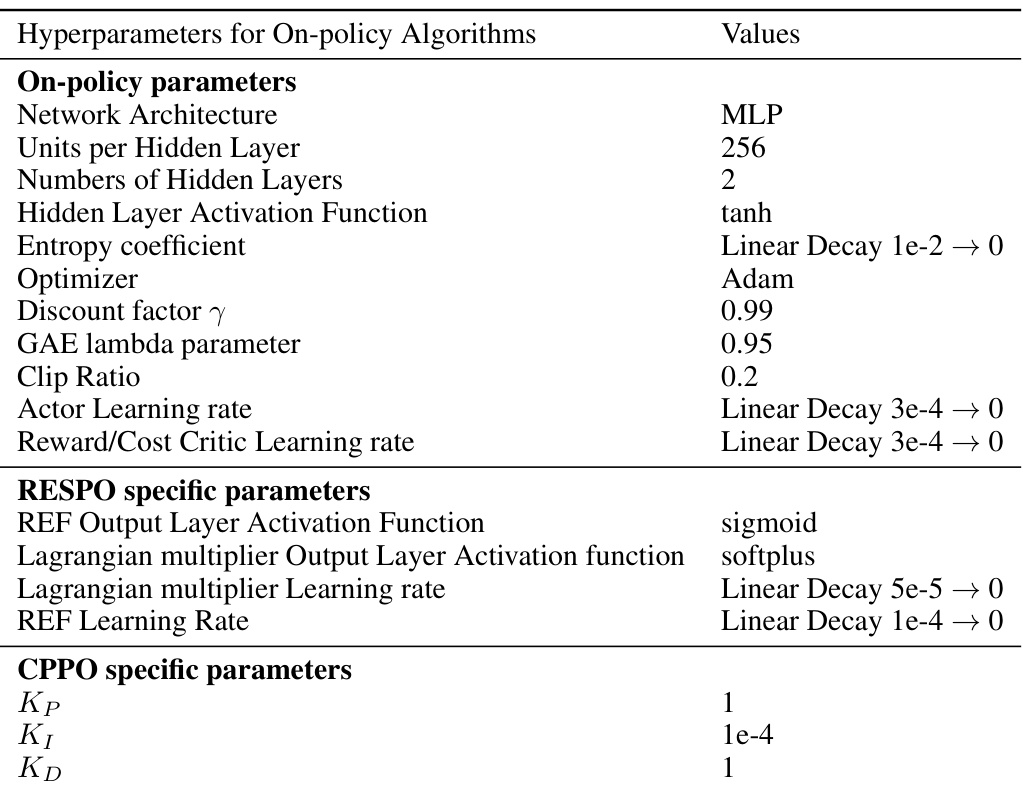
🔼 This table lists the hyperparameter settings used for the on-policy reinforcement learning algorithms in the paper. It includes parameters for the network architecture, optimization, and algorithm-specific settings such as the GAE lambda parameter and clip ratio for PPO, and the Lagrangian multiplier learning rate for RESPO.
read the caption
Table 1: Hyperparameter Settings for On-policy Algorithms
In-depth insights#
Reach-Avoid Problem#
The reach-avoid problem is a fundamental control problem focusing on steering a system to a desired goal region (reach) while simultaneously avoiding unsafe regions (avoid). This often involves navigating complex dynamics, which makes it challenging to solve. Optimal solutions typically require sophisticated techniques like Hamilton-Jacobi reachability analysis, but these methods can be computationally expensive and may not scale well for high-dimensional systems. The introduction of a cumulative cost adds another layer of complexity, transforming it into a minimum-cost reach-avoid problem. This variation necessitates finding not just any safe trajectory to the goal but the most efficient one, further increasing the computational burden. Reinforcement learning (RL) offers a potential approach, but the problem’s structure is not inherently compatible with standard RL algorithms. The paper explores this challenge, proposing a novel method to address the minimum-cost reach-avoid problem through clever problem reformulation and a specialized RL algorithm. The key innovation lies in transforming the constrained optimization into an equivalent unconstrained problem in a higher-dimensional space, making the use of RL methods more tractable.
RC-PPO Algorithm#
The RC-PPO algorithm presents a novel approach to solving minimum-cost reach-avoid problems by cleverly combining reinforcement learning with reachability analysis. Instead of directly optimizing a weighted sum of reach and cost, it transforms the problem into a reachability problem on an augmented state space. This augmented space cleverly encodes both the reach-avoid constraints and the cumulative cost, enabling the algorithm to find policies that minimize cost while satisfying constraints. A two-phase RL framework is used, first learning a stochastic policy and value function conditioned on a cost upper bound using PPO, then refining this solution to find the optimal cost bound. This approach avoids the suboptimality issues associated with combining objectives using a weighted sum, offering a path to finding truly optimal solutions. Empirical results demonstrate that RC-PPO achieves significantly lower cumulative costs compared to existing methods on various benchmark tasks, all while maintaining comparable reach rates. This highlights the effectiveness of the augmented state approach and the two-phase training strategy in addressing the complexities of constrained reinforcement learning.
Empirical Results#
The Empirical Results section of a research paper is crucial for validating the claims made in the introduction and methods. A strong Empirical Results section will present data in a clear, concise and compelling manner. Visualizations such as graphs and tables are essential for effectively communicating complex data. It should meticulously describe the experimental setup, including datasets, metrics, and statistical significance testing, to ensure reproducibility. The discussion should clearly explain whether the results support the hypotheses and discuss any unexpected findings. It’s important to compare the performance of the proposed method with existing baselines to demonstrate its advantages. Quantifiable improvements, even small ones when statistically significant, are key. Additionally, acknowledging limitations and potential biases inherent in the data or methodology helps to strengthen the overall credibility and impact of the study.
Limitations#
The research paper’s limitations section would critically analyze the shortcomings and constraints of the proposed RC-PPO algorithm. Deterministic dynamics are a major limitation, as the algorithm’s theoretical foundation relies on this assumption, which may not accurately reflect real-world scenarios with stochasticity and noise. The use of augmented dynamics, while simplifying the problem, could lead to suboptimal solutions if the augmented state space does not capture all relevant aspects of the original problem. Further limitations likely include considerations of computational cost and scalability, particularly the cost of online root-finding to determine the optimal cost upper bound for each state. Generalization to other environments and tasks beyond those explicitly tested should be investigated. Finally, the discussion should mention the reliance on specific hyperparameters and the sensitivity of performance to their selection, highlighting the need for robust tuning methods.
Future Work#
The paper’s ‘Future Work’ section would ideally delve into several key areas. Extending RC-PPO to handle stochastic dynamics is crucial for real-world applicability, as deterministic models rarely capture the complexity of real systems. Addressing the limitations of the augmented state representation, which can lead to suboptimal policies in specific scenarios, is essential. Investigating the convergence properties of the two-phase approach more rigorously would bolster the theoretical foundation of the method. Developing better methods for the cost upper-bound estimation in phase 2 would enhance the efficiency and effectiveness of the algorithm. Finally, exploring the algorithm’s scalability and robustness under more complex settings with a higher-dimensional state space is needed to confirm its effectiveness in a broader range of real-world tasks.
More visual insights#
More on figures

🔼 This figure shows six different benchmark tasks used to evaluate the performance of the proposed RC-PPO algorithm. Each task involves reaching a green goal region while avoiding a red unsafe region. The tasks vary in complexity and dynamics, representing a diverse set of challenges for minimum-cost reach-avoid problems.
read the caption
Figure 2: Illustrations of the benchmark tasks. In each picture, red denotes the unsafe region to be avoided, while green denotes the goal region to be reached.
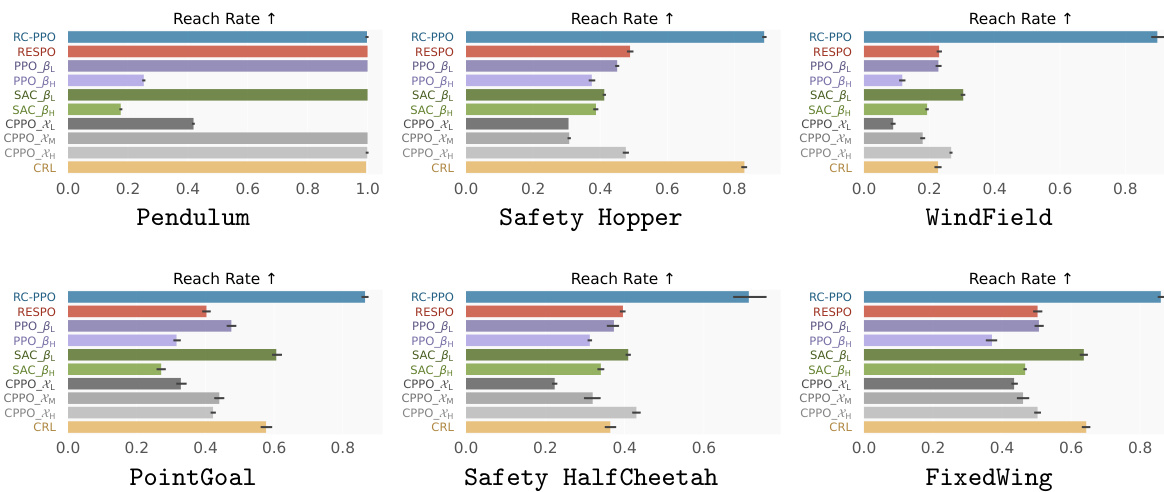
🔼 This figure displays the reach rates achieved by RC-PPO and several baseline reinforcement learning algorithms across six different benchmark tasks under a sparse reward setting. The results clearly show that RC-PPO consistently outperforms all other algorithms, achieving the highest reach rate in every task. Error bars indicate the standard error of the mean, providing a measure of the uncertainty associated with the reach rate measurements.
read the caption
Figure 3: Reach rates under the sparse reward setting. RC-PPO consistently achieves the highest reach rates in all benchmark tasks. Error bars denote the standard error.

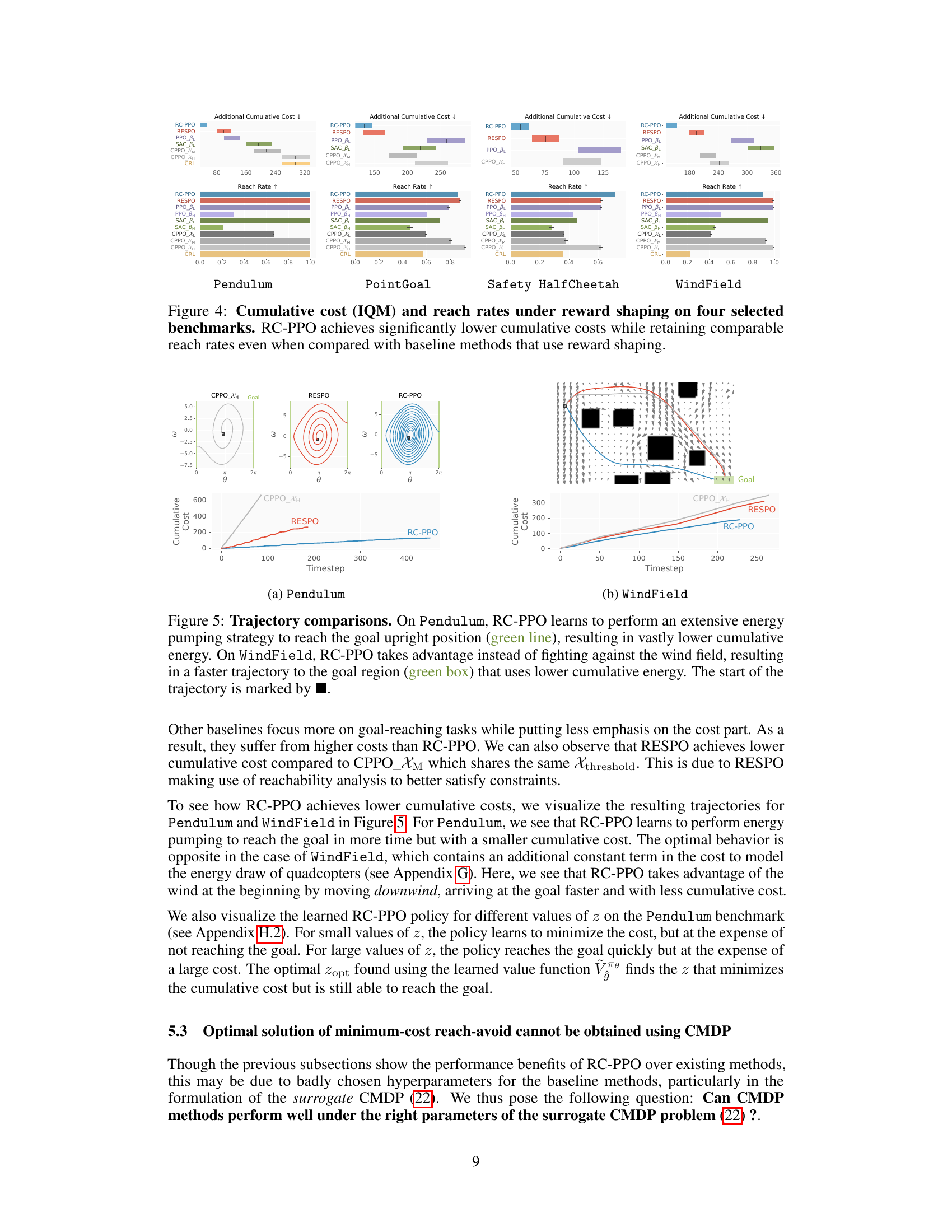
🔼 This figure compares the performance of different reinforcement learning algorithms on two tasks, FixedWing and Safety Hopper, in terms of both cumulative cost and reach rate. RC-PPO consistently achieves significantly lower cumulative costs while maintaining comparable reach rates to other methods, demonstrating its efficiency and effectiveness in solving minimum-cost reach-avoid problems.
read the caption
Figure 7: Cumulative cost and reach rates of the final converged policies.

🔼 This figure compares the trajectories of RC-PPO and other baselines on the Pendulum and WindField environments. In Pendulum, RC-PPO uses energy pumping to reach the goal more slowly but with lower cumulative cost. In WindField, RC-PPO leverages the wind to reach the goal faster and with less energy consumption.
read the caption
Figure 5: Trajectory comparisons. On Pendulum, RC-PPO learns to perform an extensive energy pumping strategy to reach the goal upright position (green line), resulting in vastly lower cumulative energy. On WindField, RC-PPO takes advantage instead of fighting against the wind field, resulting in a faster trajectory to the goal region (green box) that uses lower cumulative energy. The start of the trajectory is marked by

🔼 This figure shows the Pareto front achieved by varying the reward function coefficients of the surrogate CMDP problem solved using PPO. The Pareto front represents the tradeoff between reach rate and additional cumulative cost. RC-PPO’s performance is plotted as a single point, demonstrating that it outperforms all points on the Pareto front, achieving both a high reach rate and a low cumulative cost.
read the caption
Figure 6: Pareto front of PPO across different reward coefficients. RC-PPO outperforms the entire Pareto front of what can be achieved by varying the reward function coefficients of the surrogate CMDP problem when solved using PPO.
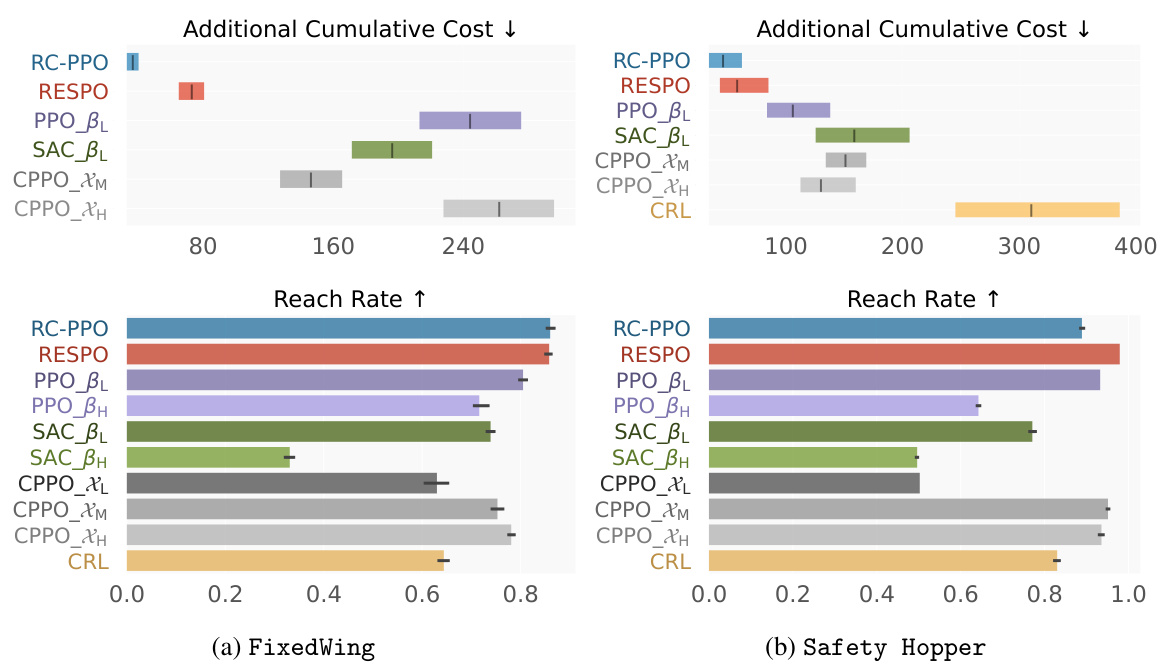
🔼 This figure compares the performance of different reinforcement learning algorithms on two benchmark tasks, FixedWing and Safety Hopper. The left half of the figure shows the cumulative cost, while the right half shows the reach rate. RC-PPO consistently outperforms other algorithms across both metrics. The chart presents a visual comparison of the algorithm performances, highlighting the superiority of RC-PPO in minimizing cumulative cost while maintaining a high reach rate.
read the caption
Figure 7: Cumulative cost and reach rates of the final converged policies.
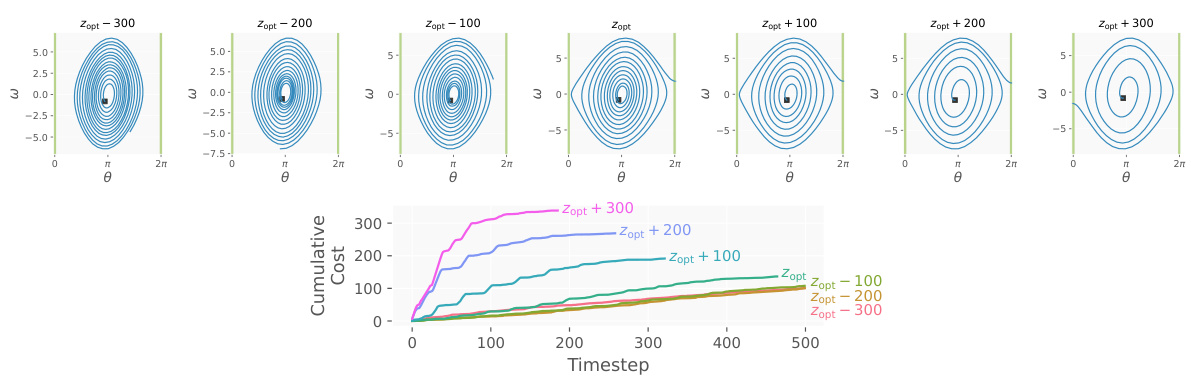
🔼 This figure visualizes the learned RC-PPO policy for different cost upper bounds (z) on the Pendulum environment. It shows how the policy changes depending on the value of z. For low z values, the policy prioritizes cost minimization, even at the cost of not reaching the goal. For high z values, the policy prioritizes reaching the goal, even if it leads to higher costs. The optimal z (zopt), found through root-finding, balances these two objectives, achieving the lowest cumulative cost while still reaching the goal. The visualizations are contour plots showing the learned policy and line graphs showing the cumulative cost over time for various z values.
read the caption
Figure 8: Learned RC-PPO policy for different z on Pendulum. For a smaller cost lower-bound z, cost minimization is prioritized at the expense of not reaching the goal. For a larger cost lower-bound z, the goal is reached using a large cumulative cost. Performing rootfinding to solve for the optimal zopt automatically finds the policy that minimizes cumulative costs while still reaching the goal.
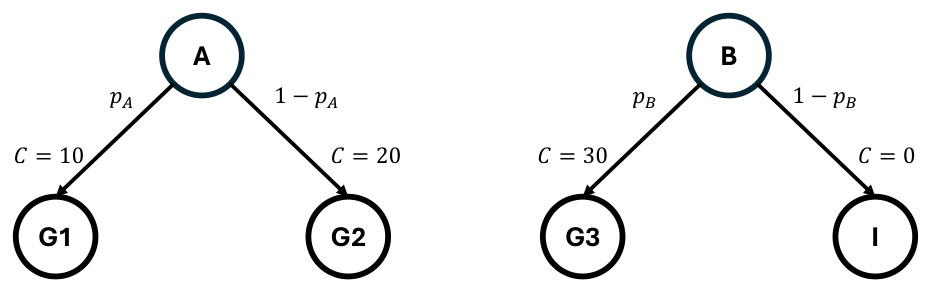
🔼 This figure presents a minimum-cost reach-avoid problem to show the limitations of CMDP-based methods. It’s a graph showing two initial states (A and B), each with two possible actions leading to different goal states (G1, G2, G3) with associated costs (C) or an absorbing state (I). The probabilities of choosing each action are denoted by pA and pB. The example demonstrates that optimizing a weighted combination of reward and cost, or using a threshold on the cost, can lead to suboptimal solutions for the original minimum-cost reach-avoid problem. The optimal solution requires considering both reaching the goal and minimizing the cost simultaneously, a challenge not directly addressed by CMDP formulations.
read the caption
Figure 9: Minimum-cost reach-avoid example to illustrate the limitation of CMDP-based formulation.
More on tables
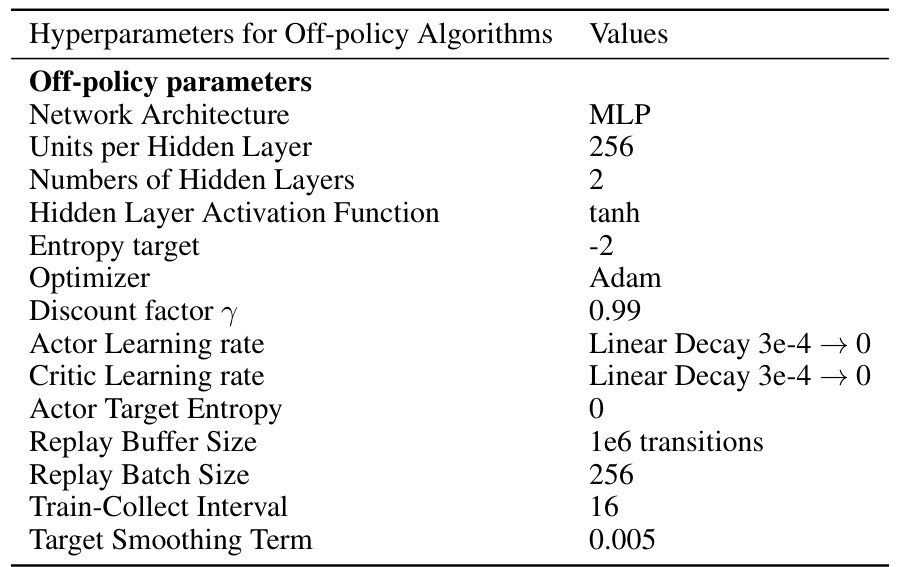
🔼 This table lists the hyperparameters used for the off-policy reinforcement learning algorithms in the paper’s experiments. It includes settings for network architecture, hidden layers, activation functions, optimizer, discount factor, learning rates, entropy target, replay buffer and batch size, training interval, and target smoothing term.
read the caption
Table 2: Hyperparameter Settings for Off-policy Algorithms

🔼 This table presents the reach rate of different reinforcement learning algorithms under varying levels of noise added to the output control. The algorithms compared include RC-PPO, RESPO, PPO with different hyperparameters (βL and βH), SAC with different hyperparameters (βL and βH), CPPO with different thresholds (XL, XM, and XH), and CRL. The noise levels are categorized as ‘Small Noise’ and ‘Large Noise.’ The table shows the robustness of each algorithm to noise in achieving the goal.
read the caption
Table 3: Reach rate of final converged policies with different levels of noise to the output control

🔼 This table shows the additional cumulative cost of different reinforcement learning algorithms when different levels of noise are added to the output control. The algorithms are compared across three noise levels: No noise, small noise, and large noise.
read the caption
Table 4: Additional cumulative cost of final converged policies with different levels of noise to the output control
Full paper#