Multi-Label Open Set Recognition

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it addresses a critical gap in multi-label learning by tackling the open-set scenario. The proposed SLAN approach offers a novel solution to a real-world problem, improving the robustness of multi-label models in dynamic environments and providing a foundation for future research in open-set multi-label recognition. This is relevant to various applications where unknown labels may emerge, such as image annotation and text categorization.

Visual Insights

#

This figure shows an example image and its associated labels to illustrate the concept of multi-label open set recognition (MLOSR). Some labels are known from the training data, while others are unknown and only appear during the testing phase. This highlights the challenge of MLOSR, where the model needs to identify both known and unknown labels.

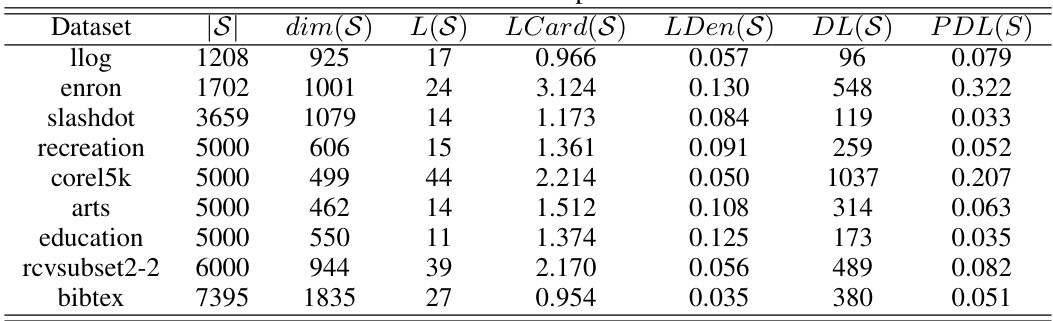
This table presents the characteristics of eight benchmark multi-label datasets used in the experiments. For each dataset, it provides the number of instances (|S|), the number of features (dim(S)), the number of class labels (L(S)), label cardinality (LCard(S)), label density (LDen(S)), the number of distinct label sets (DL(S)), and the proportion of distinct label sets (PDL(S)). These characteristics help to understand the nature of each dataset and its suitability for evaluating multi-label learning models.

In-depth insights

#

MLOSR Framework

#

The proposed MLOSR (Multi-Label Open Set Recognition) framework tackles a crucial problem in multi-label learning: handling unknown labels during testing. It’s a significant advancement because traditional multi-label methods assume all labels are known beforehand. The core of the framework likely involves a novel approach to differentiate between known and unknown labels by leveraging sub-labeling information and structural information from the feature space. This is achieved by enriching sub-label information using structural relationships among training instances, allowing the model to discern patterns indicating the presence of unseen labels. The framework likely employs an algorithm that combines open-set recognition with a multi-label classifier, using alternating optimization or similar techniques to update these two models simultaneously. A key challenge addressed is disentangling known and unknown labels, often co-occurring in real-world data, which is a significant hurdle for existing methods. The success of this framework hinges on effectively extracting and utilizing subtle, informative patterns from the data to accurately identify instances with unseen labels in a multi-label context.

SLAN Algorithm

#

The SLAN algorithm, designed for Multi-label Open Set Recognition (MLOSR), is a novel approach that cleverly addresses the challenges of classifying instances with both known and unknown labels. Its core innovation lies in enriching sub-labeling information using structural relationships in the feature space. This is achieved by leveraging sparse reconstruction techniques to capture the underlying manifold structure, effectively differentiating sub-labeling information from holistic supervision. This allows the algorithm to robustly identify unknown labels which frequently co-occur with known ones. The algorithm then uses this enriched information to improve the performance of a unified multi-label classifier and an open set recognizer. A key strength of SLAN is its use of alternating optimization, enabling it to simultaneously learn from both the sub-labeling and holistic label information, resulting in improved accuracy and more robust handling of open set conditions in multi-label settings. This makes SLAN a significant advancement for MLOSR problems, where traditional methods often struggle.

Structural Info

#

The heading ‘Structural Info’ likely refers to a section detailing how the authors leverage structural information within the data’s feature space to improve multi-label open set recognition (MLOSR). This likely involves techniques that go beyond simple feature extraction and consider relationships between features. A common method would be manifold learning, which assumes data points lying close together in feature space are semantically similar. The authors might use techniques like sparse reconstruction to model these relationships, effectively creating a graph where nodes represent data points and edges denote relationships. This graph structure captures latent relationships, enriching the representation and aiding in the classification of known and unknown labels. Sub-label information is likely integrated with this structural information, meaning the relationships in the feature space are used to inform how the system understands and predicts individual labels as well as the set of labels assigned to an instance. The key is that the structural approach is designed to improve the differentiation between instances with known labels only and those also containing unknown labels. This is crucial in open-set scenarios as it addresses ambiguity caused by overlapping features of known and unknown classes.

Open Set Risk

#

In the context of multi-label learning, open set risk quantifies the uncertainty associated with encountering unknown labels during testing. Traditional multi-label learning assumes a closed set where training and testing labels are identical. However, real-world applications often present open-set scenarios, introducing unforeseen labels. This necessitates methods that not only predict known labels but also identify and handle those unknown. A model with low open set risk is crucial as it minimizes misclassifications of novel labels as known ones, thus enhancing robustness and generalization capability. Quantifying open set risk effectively involves differentiating between genuine unknowns and known labels co-occurring unexpectedly. This requires sophisticated techniques beyond standard classification accuracy, potentially involving anomaly detection or uncertainty estimation to properly manage the open set challenge.

Future Works

#

Future research directions stemming from this multi-label open set recognition (MLOSR) work could explore several avenues. Extending the approach to handle extremely large-scale datasets (extreme multi-label learning) is crucial for real-world applicability. The current method’s reliance on feature space structural information might be less effective with high-dimensional data, therefore, investigating more robust feature representation learning techniques is important. Furthermore, developing deep learning-based MLOSR models could improve performance and scalability. Finally, a more comprehensive set of evaluation metrics tailored to the unique challenges of open set multi-label prediction needs to be developed and standardized for future comparative analyses.

More visual insights

#

More on tables

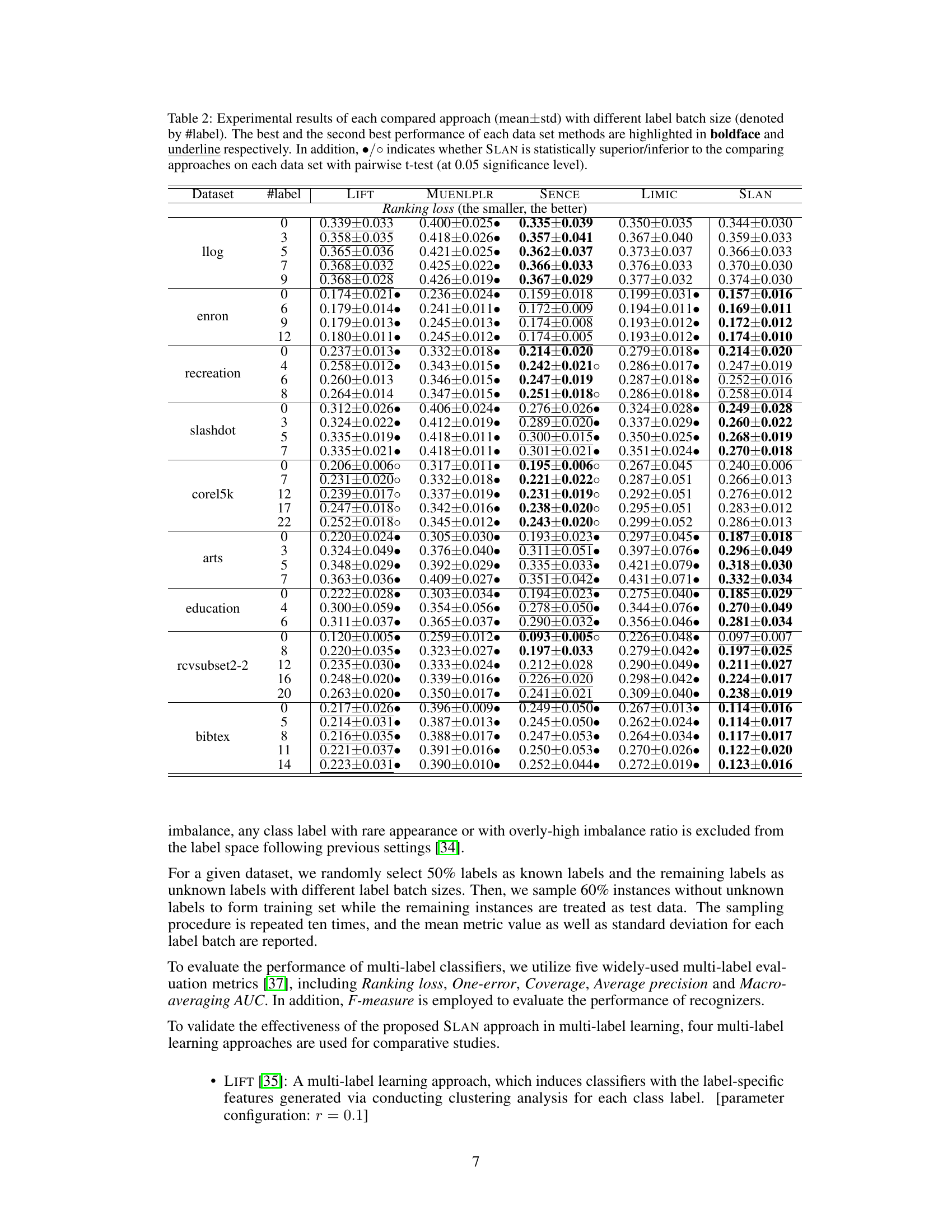
This table shows the experimental results comparing SLAN with other methods using different label batch sizes. The table presents ranking loss for multiple datasets across various numbers of labels. Statistical significance (p<0.05) is indicated to show whether SLAN outperforms other methods.

This table presents the experimental results comparing SLAN’s performance against other methods across various datasets. Different label batch sizes were used. The table shows the mean and standard deviation of the ranking loss for each method and dataset. Statistical significance is indicated using a pairwise t-test at the 0.05 level.

This table presents the experimental results comparing the performance of SLAN against other methods on several multi-label datasets. The results are shown in terms of ranking loss, using different batch sizes of labels. Statistical significance (p<0.05) is indicated with symbols to show whether SLAN outperforms other methods.

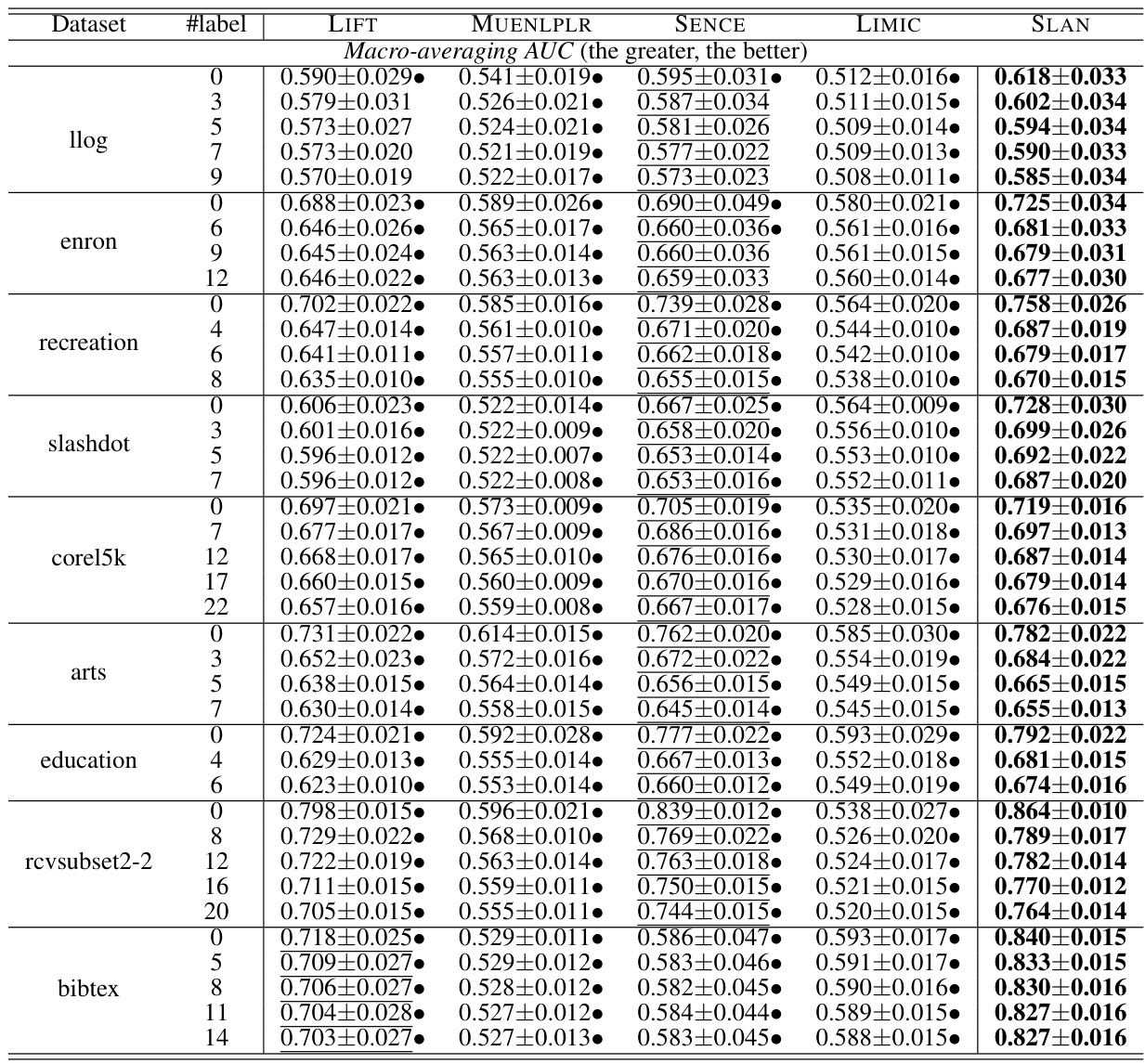
This table presents the Macro-averaging AUC scores achieved by different multi-label learning approaches (LIFT, MUENLPLR, SENCE, LIMIC, and SLAN) across various datasets under different experimental conditions. Each dataset is tested with varying numbers of labels considered as known (indicated by #label), allowing for comparison of performance in open-set scenarios. The best and second-best results for each dataset and method are highlighted, along with statistical significance testing to show if SLAN outperforms others.

This table presents the results of pairwise t-tests comparing the performance of the proposed SLAN approach against four other multi-label learning methods (LIFT, MUENLPLR, SENCE, LIMIC) across five different evaluation metrics (Ranking loss, One-error, Coverage, Average precision, Macro-averaging AUC). For each metric, the table shows the number of times SLAN performed better, tied, or worse than each of the other methods. This provides a statistical assessment of the relative performance of SLAN.

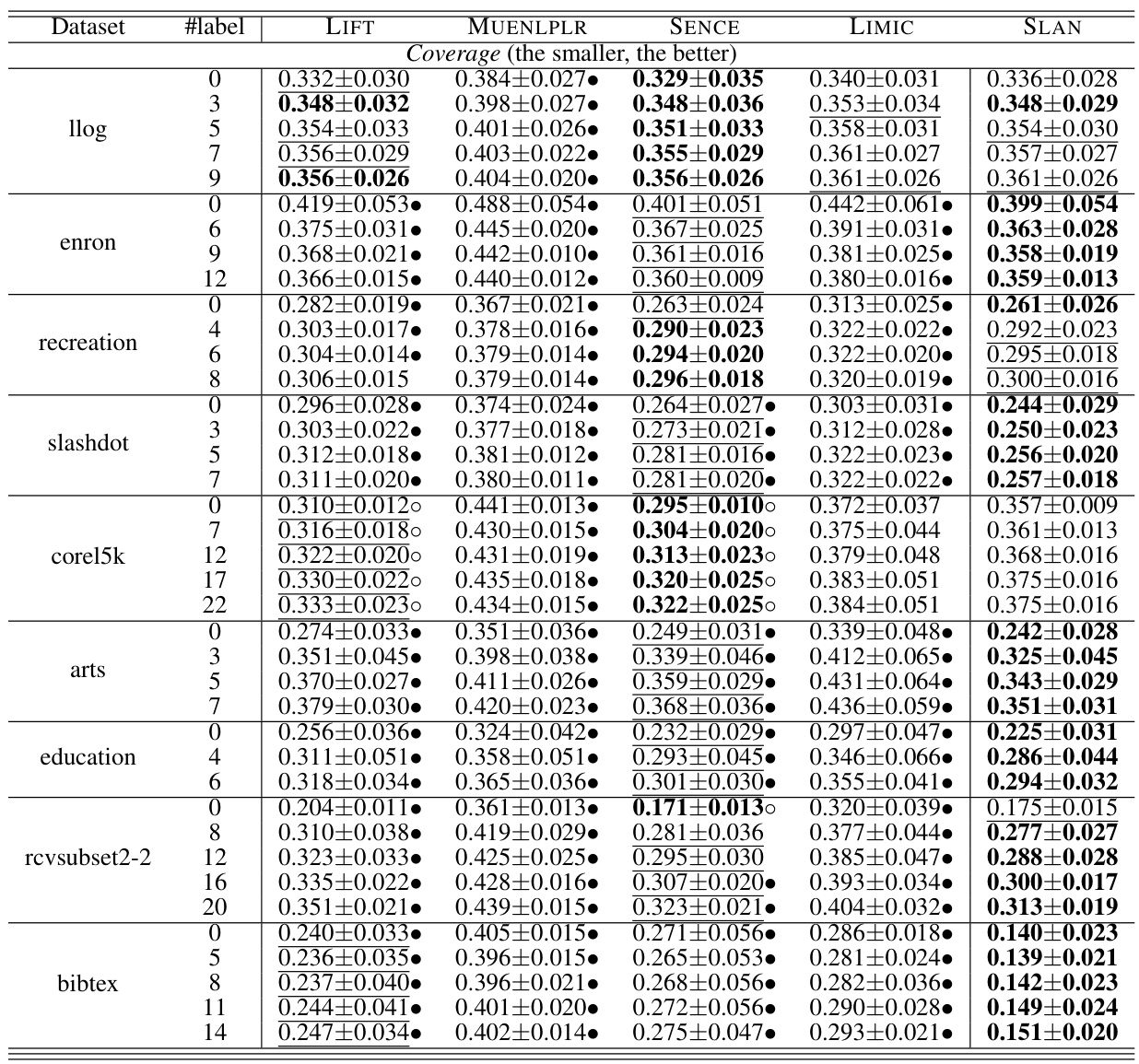
This table presents the results of five multi-label classification approaches (LIFT, MUENLPLR, SENCE, LIMIC, and SLAN) evaluated using the Coverage metric. The experiment is repeated with different batch sizes of labels. The best and second-best results for each dataset and label batch are highlighted. Statistical significance testing (pairwise t-test) compares SLAN against the other methods.

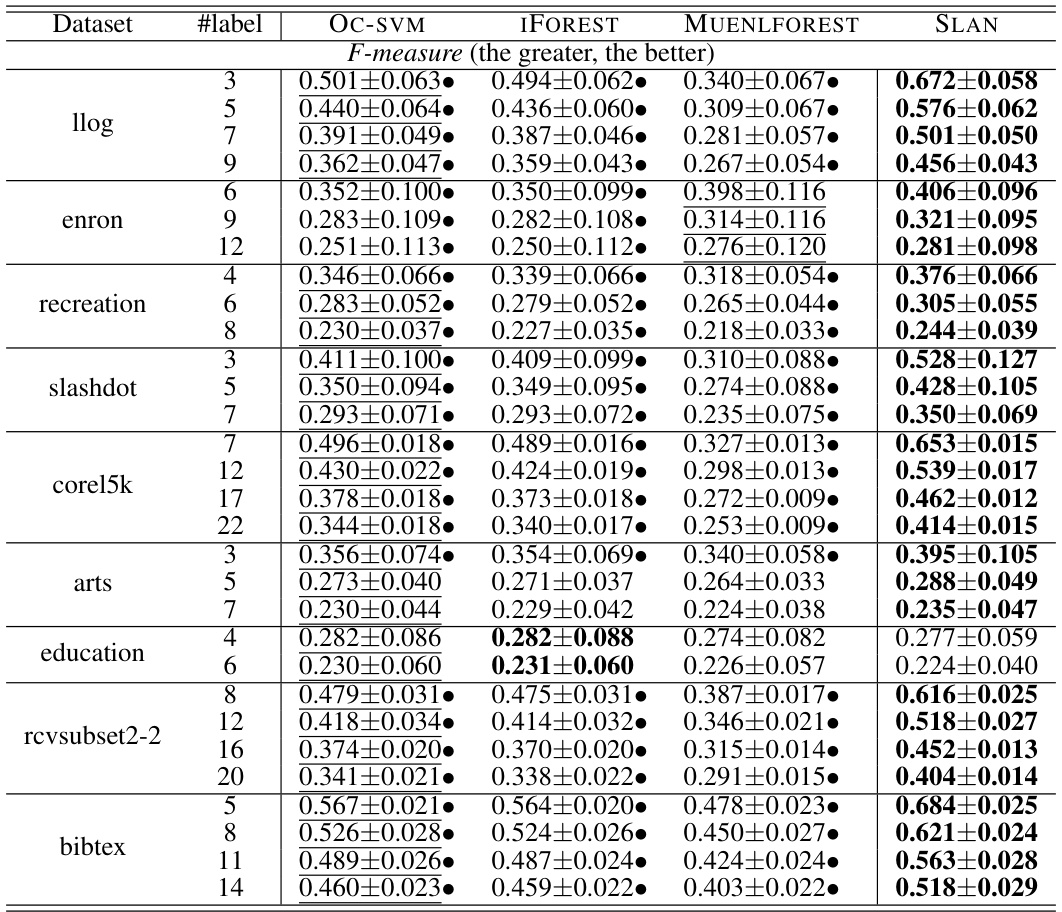
This table presents the results of pairwise t-tests comparing the performance of SLAN against three other anomaly detection methods (OC-SVM, IFOREST, and MUENLFOREST) across multiple datasets. The numbers represent the counts of wins, ties, and losses for SLAN in terms of the F-measure metric. A win indicates that SLAN’s performance is statistically significantly better than the compared method; a tie indicates no significant difference; and a loss means the compared method performed significantly better.

This table presents the experimental results comparing SLAN with four other multi-label learning approaches across multiple datasets. The results are shown using different label batch sizes, highlighting the best and second-best performing methods. Statistical significance is also indicated via a pairwise t-test.

Full paper

#