Even Sparser Graph Transformers

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with large-scale graph data and graph neural networks. It directly addresses the memory limitations of existing Graph Transformers, a significant bottleneck in many applications. By introducing Spexphormer, the research offers a practical and effective solution, potentially accelerating progress in areas like social network analysis, knowledge graphs, and drug discovery.

Visual Insights

#

This figure illustrates the two-stage training process of the Spexphormer model. The first stage trains a small-width network (Attention Score Estimator Network) to estimate pairwise attention scores. This network uses a combination of graph edges, self-loops, and expander graph edges for its attention mechanism. The attention scores are then used to create a sparse attention graph for a second, larger network. This sparse graph is used to train the final, wider network. The figure highlights the differences in the attention mechanism between the two networks, particularly the normalization of V in the first network.

This table presents the ablation study results for Spexphormer on four datasets: two homophilic (Photo and Computer) and two heterophilic (Minesweeper and Tolokers). The metrics used are accuracy for the homophilic datasets and ROC-AUC for the heterophilic datasets. The table compares the performance of the full Spexphormer model against several variants: Spexphormer-uniform (using uniform sampling instead of attention-based sampling), Spexphormer-max (selecting only the top-k edges instead of sampling), Spexphormer without temperature annealing, and Spexphormer without layer normalization. The ‘Initial Network’ row shows the performance of the small, initial network used for attention score estimation. The results demonstrate the impact of different design choices in the Spexphormer architecture.

In-depth insights

#

Sparse Transformers

#

Sparse Transformer models aim to address the computational limitations of traditional Transformers, particularly their quadratic complexity with respect to sequence length. This is achieved by selectively attending to only a subset of input tokens, rather than all possible pairwise combinations. Various techniques exist for sparsifying attention, including using locality-sensitive hashing, random sampling, or learned attention mechanisms that prioritize relevant tokens. The benefits of sparsity include reduced memory and computational requirements, enabling the processing of longer sequences or larger datasets. However, sparse Transformers require careful design to avoid performance degradation, as overly aggressive sparsification can lead to information loss and hinder the model’s ability to capture long-range dependencies. A key challenge is to strike a balance between computational efficiency and model accuracy. The choice of sparsification strategy significantly influences the trade-off between these two objectives. Furthermore, research continues to explore innovative sparsification techniques and efficient implementations to maximize the advantages of sparse Transformers in various applications.

Two-Stage Training

#

The proposed two-stage training approach offers a compelling strategy for improving the efficiency and scalability of graph transformers. The first stage involves training a narrow network to learn initial attention weights. This initial model, due to its smaller size, can be trained on a CPU, overcoming GPU memory limitations. The second stage utilizes the learned attention weights from the narrow network to sparsify the graph before training a wider, more powerful network. This sparsity drastically reduces computational complexity without sacrificing accuracy. This approach elegantly addresses the quadratic complexity challenge commonly associated with graph neural networks and allows for scaling to larger graphs that are typically intractable for traditional methods. The two-stage method combines the advantages of both small and large networks in a novel way, providing a significant advancement in the field of efficient graph neural network training. The initial stage is used to identify critical edges in the graph, enabling the second stage to focus on these crucial connections, thereby efficiently improving learning performance while minimizing computational cost. The effectiveness of this approach is empirically validated, demonstrating that this training strategy provides significant efficiency gains for large-scale applications while maintaining excellent performance.

Attention Score Est.

#

The heading ‘Attention Score Est.’ likely refers to a crucial section detailing a method for estimating attention scores in a graph neural network. This is a significant aspect, as attention mechanisms are computationally expensive, especially in large graphs. The core idea is likely to approximate attention scores using a smaller, faster network to create a sparse graph. This two-stage process starts with training a low-width network to identify important connections, then training a wider model only on this sparse graph. This approach is particularly valuable for scaling graph transformers, enabling them to handle much larger datasets than traditional methods. Theoretical analysis within this section might justify the efficacy of this estimation procedure, providing insights into how well attention scores from a smaller network reflect those of a larger network, under specific conditions. The success of ‘Attention Score Est.’ directly impacts the model’s efficiency and scalability, making it a key component of the research.

Scalability Analysis

#

A thorough scalability analysis of a graph transformer model would involve examining its computational and memory complexities as the size of the input graph grows. Key aspects to consider include the runtime scaling of attention mechanisms (e.g., quadratic complexity for dense attention), the impact of graph sparsification techniques on both accuracy and efficiency, and the effectiveness of any employed batching or sampling strategies. The analysis should also quantify the memory footprint of the model, including the storage requirements for node and edge features, intermediate activations, and model parameters. Empirical results demonstrating scalability on various graph sizes and datasets would be crucial. Furthermore, a strong analysis should compare the proposed approach’s scalability to existing graph neural network (GNN) methods, providing a quantitative evaluation of performance gains or trade-offs. Finally, any theoretical guarantees on the model’s scalability should be included, along with a discussion of the limitations and potential bottlenecks under different graph properties and model configurations. This multifaceted approach helps determine the model’s suitability for large-scale graph tasks and identifies directions for future improvements.

Future Directions

#

Future research could explore several promising avenues. Improving the efficiency of the attention score estimator network is crucial; reducing its computational cost would allow scaling to even larger graphs. Developing more sophisticated sparsification techniques that better capture the essence of the full attention mechanism is another key area. Theoretical investigations into the relationship between network width and attention score consistency could yield deeper insights, leading to more robust and efficient model architectures. Exploring alternative sampling methods might improve efficiency and scalability. Finally, the application of Spexphormer to diverse graph datasets and tasks, and the extension to dynamic graphs will be valuable to test the limits and uncover further implications.

More visual insights

#

More on figures

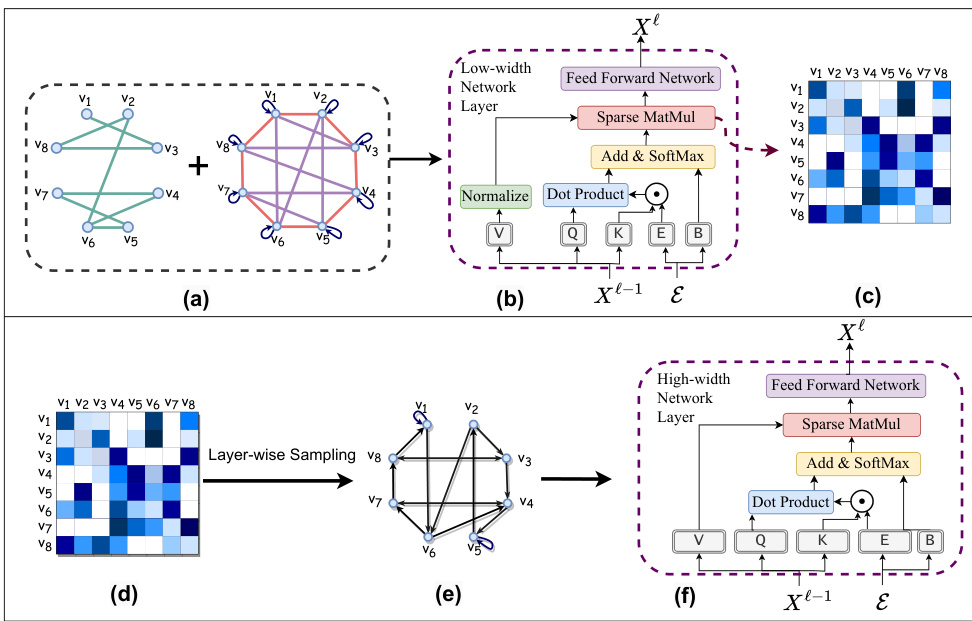
This figure illustrates the two-phase training process of the Spexphormer model. The first phase uses a low-width network with a specific attention mechanism (combining graph edges, expander graphs, and self-loops) to estimate pairwise attention scores. These scores are then used in a second phase to create a sparse attention graph for training a higher-width network. The figure visually depicts each step of the process, showing the attention mechanisms, the sparsification process, and the final sparse graph used for training.

This figure presents the results of an experiment to evaluate how well smaller networks can estimate attention scores of larger networks. The energy distance, a measure of the dissimilarity between two probability distributions, was calculated between the attention score distributions of networks with different widths (4, 8, 16, 32, 64) and a reference network with width 64. Two baseline distributions, uniform and random, were also compared. The results, shown separately for Actor and Photo datasets with and without expander graphs, indicate that smaller networks yield reasonably accurate estimates of attention scores.

This figure illustrates the two-phase training process of the Spexphormer model. The first phase uses a small-width network (Attention Score Estimator Network) with a sparse attention mechanism to estimate pairwise attention score patterns. This network combines graph edges, self-loops, and expander graph edges to learn which neighbor nodes are most informative for each node. The learned attention scores are then used to sparsify the graph for the second phase, creating a sparse graph used to train a larger network (High-width Network). The final network, trained on this sparser graph, achieves better efficiency than the original Exphormer network.

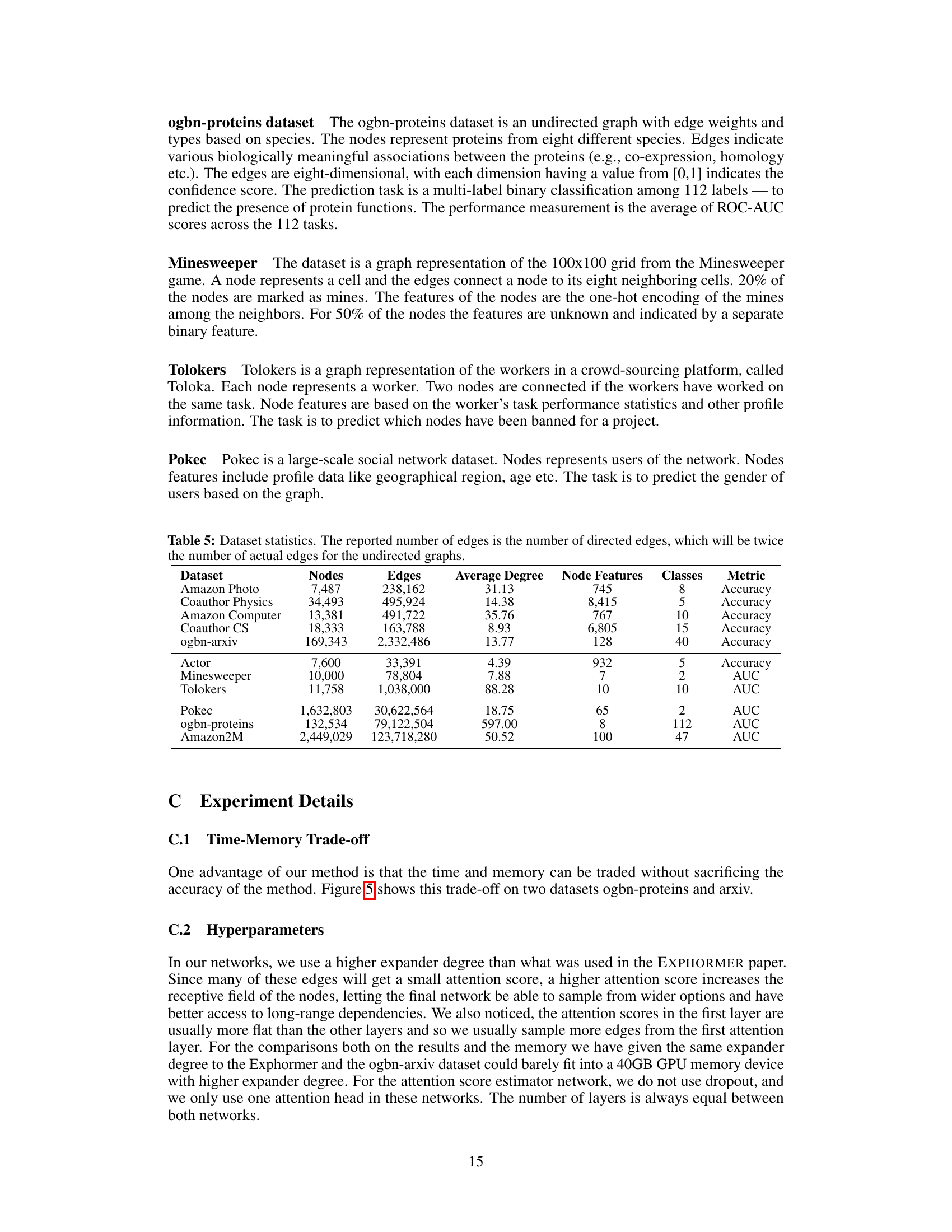
This figure shows the relationship between memory usage, time per epoch, and batch size for training the model on two large graph datasets: ogbn-proteins and ogbn-arxiv. The plots demonstrate a trade-off: increasing the batch size reduces the time per epoch but increases memory consumption. Importantly, the test accuracy/AUC remains relatively consistent across different batch sizes, highlighting the flexibility of the proposed approach to balance computational resources and performance.

More on tables

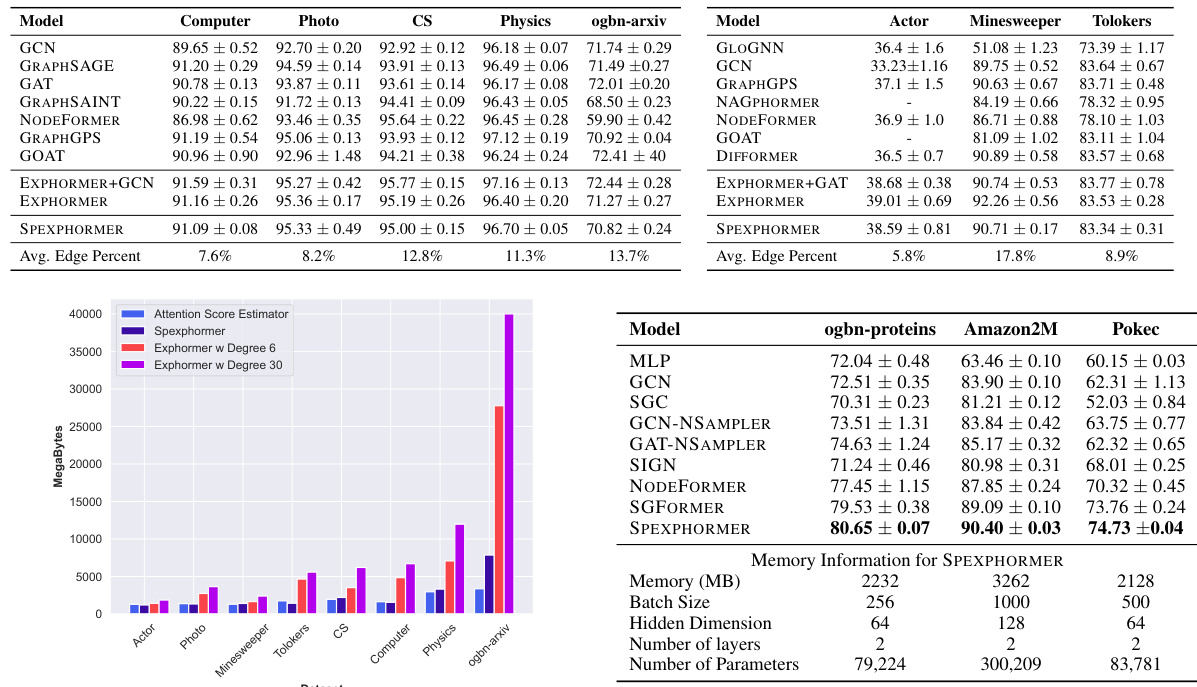
This table compares the performance of Spexphormer against other Graph Neural Networks (GNNs) on eight datasets. Five datasets exhibit homophily (similar nodes tend to cluster together), while three datasets show heterophily (nodes with dissimilar features tend to be close). The metrics used are ROC-AUC (for Minesweeper and Tolokers) and accuracy (for the others). The table also shows the average edge ratio, which represents the sparsity of the Spexphormer’s attention mechanism relative to the original graph.

This table presents the statistics of eleven graph datasets used in the paper’s experiments. For each dataset, it provides the number of nodes, number of edges, average node degree, number of node features, number of classes, and the evaluation metric used (Accuracy or AUC). The table helps to understand the scale and characteristics of the datasets, which are crucial for interpreting the experimental results. The note clarifies that edge counts represent directed edges, which are double the number of undirected edges for undirected graphs.

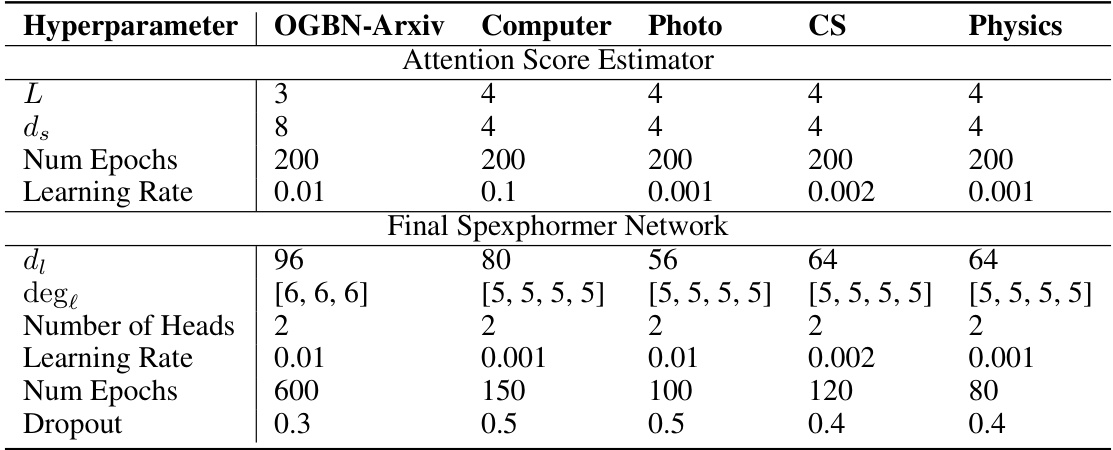
This table shows the hyperparameters used to train both the Attention Score Estimator Network and the final Spexphormer Network on five homophilic datasets: ogbn-arxiv, Computer, Photo, CS, and Physics. For each dataset, it specifies the number of layers (L), the width of the small network (ds), the number of training epochs, the learning rate, the width of the larger network (d_l), the number of sampled edges per layer (deg_l), the number of attention heads, the learning rate for the larger network, the number of training epochs for the larger network, and the dropout rate. The hyperparameters are tuned for each dataset individually to achieve optimal performance.

This table shows the hyperparameters used for training both the attention score estimator network and the final Spexphormer network on three heterophilic datasets: Actor, Minesweeper, and Tolokers. It lists the number of layers (L), the width of the estimator network (ds), the number of training epochs, the learning rate, the width of the final network (d_l), the number of sampled neighbors per layer (deg_l), the number of attention heads, the learning rate of the final network, the number of training epochs for the final network, and the dropout rate. These hyperparameters were tuned separately for each dataset to optimize performance.

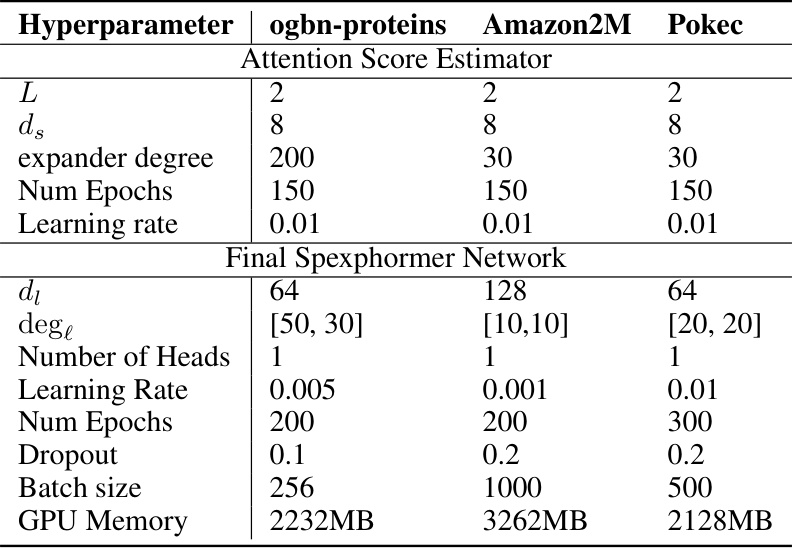
This table shows the hyperparameters used for training the attention score estimator network and the final Spexphormer network for three large graph datasets: ogbn-proteins, Amazon2M, and Pokec. The hyperparameters include the number of layers (L), the width of the smaller network (ds), the expander degree, the number of epochs, the learning rate, the width of the larger network (di), the number of edges per layer (dege), the number of heads, the learning rate, the number of epochs, the dropout rate, the batch size, and the GPU memory used.

Full paper

#