↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current Neural Radiance Fields (NeRFs) struggle with sparse and unconstrained views because their reconstruction quality heavily relies on the distribution of training camera poses and triangulation quality. Existing methods do not explicitly model this provenance information, leading to suboptimal results.
ProvNeRF addresses this by innovatively modeling each point’s provenance (likely visible locations) as a stochastic field. This is achieved by extending implicit maximum likelihood estimation (IMLE) to functional space. The results demonstrate significant improvements in novel view synthesis and uncertainty estimation compared to existing baselines, especially in challenging sparse view scenarios. This method enriches the NeRF model by incorporating information about triangulation quality, leading to more robust and accurate 3D scene reconstruction.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles a critical limitation in Neural Radiance Field (NeRF) reconstruction: the dependence on training camera poses and triangulation quality. By explicitly modeling per-point provenance as a stochastic field, ProvNeRF significantly improves novel view synthesis and uncertainty estimation, especially under challenging sparse and unconstrained view settings. This opens avenues for enhancing NeRF robustness and reliability in various applications and inspires further research into uncertainty modeling and improved triangulation techniques within the field.
Visual Insights#
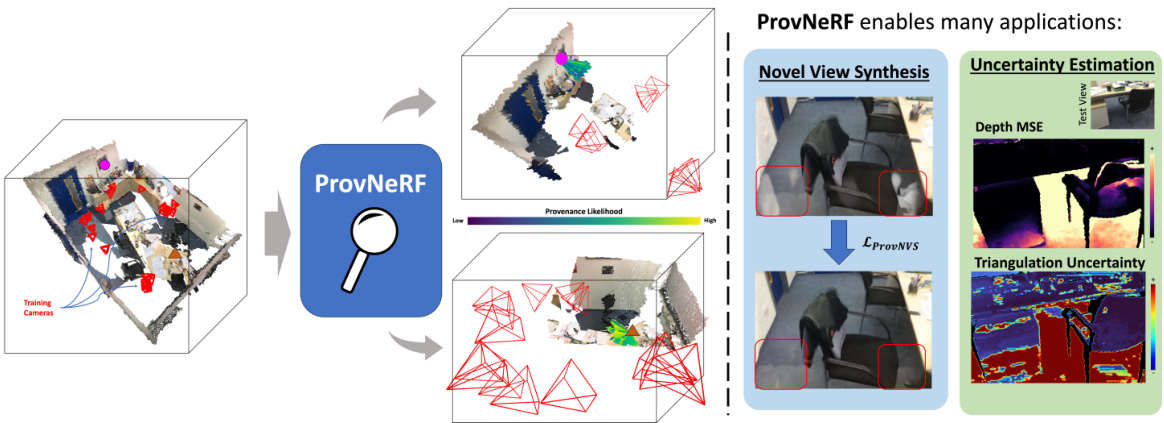
This figure illustrates the core concept of ProvNeRF. The left side shows how ProvNeRF models the provenance (likely locations of visibility) for each 3D point in a scene as a stochastic field. Arrows represent the likely viewing locations. The right side demonstrates the applications enabled by ProvNeRF: improved novel view synthesis (creating realistic images from unseen angles) and better uncertainty estimation (quantifying confidence in the scene reconstruction).
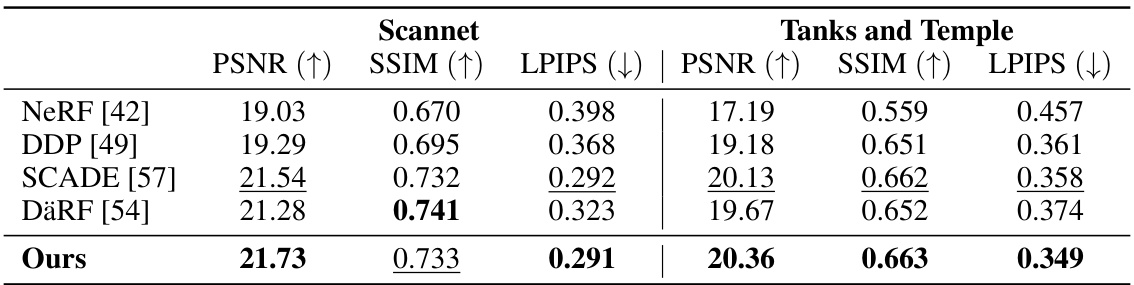
This table presents a quantitative comparison of novel view synthesis results on the Scannet and Tanks and Temple datasets. The metrics used are PSNR, SSIM, and LPIPS. The results show that the proposed ProvNeRF method outperforms existing state-of-the-art methods in terms of these metrics, indicating improved image quality and visual fidelity in novel views.
In-depth insights#
ProvNeRF: Point Provenance#
ProvNeRF introduces a novel approach to Neural Radiance Fields (NeRFs) by explicitly modeling the provenance of each 3D point. Instead of treating each point’s appearance as solely determined by its 3D coordinates, ProvNeRF considers the distribution of camera viewpoints from which that point is likely visible. This “provenance” is represented as a stochastic field, capturing the uncertainty inherent in reconstructing 3D scenes from limited and potentially noisy views. Modeling this provenance significantly improves the NeRF’s ability to handle sparse and unconstrained view settings. By leveraging this additional information during training, ProvNeRF enhances novel view synthesis and uncertainty estimation. This innovative method addresses the limitations of existing NeRFs which often struggle with limited or unevenly distributed camera poses, paving the way for more robust and reliable 3D scene reconstruction.
Stochastic Field Modeling#
Stochastic field modeling, in the context of the provided research paper, offers a powerful approach to represent the uncertainty inherent in the process of reconstructing 3D scenes from 2D images. Instead of deterministic models, which assign fixed properties to each point, stochastic fields model the probability of a point being visible from various camera locations. This approach directly addresses the challenges of sparse and unconstrained view settings, where triangulation quality significantly impacts reconstruction accuracy. The key advantage lies in capturing the distribution of possible viewpoints, which is essential for estimating the uncertainty and improving the accuracy of the 3D model. Probabilistic methods are employed to learn these distributions, enabling the model to quantify its uncertainty. This leads to more robust and reliable 3D scene reconstructions, as the model inherently accounts for the uncertainty introduced by data scarcity and view limitations.
Novel View Synthesis#
The section on “Novel View Synthesis” likely details how the ProvNeRF model improves the generation of realistic images from unseen viewpoints. ProvNeRF’s approach of modeling per-point provenance as a stochastic field is crucial here, enriching the model’s understanding of 3D scene geometry and camera placement. This leads to more robust and accurate novel view synthesis, especially in challenging scenarios with sparse or unconstrained viewpoints. The evaluation likely involves quantitative metrics such as PSNR and SSIM, comparing ProvNeRF’s performance against existing methods. Qualitative results, showcasing improved image quality and the reduction of artifacts, might also be presented. A key aspect would be demonstrating ProvNeRF’s superiority in handling occlusions and improving triangulation, thereby mitigating issues common in traditional NeRF approaches under limited viewpoints. The authors likely discuss how the learned provenance field informs the rendering process, contributing to better visual fidelity and consistency in novel views.
Uncertainty Estimation#
The research explores uncertainty modeling in neural radiance fields (NeRFs), a crucial aspect for robust scene representation and downstream tasks. The authors address the limitations of existing methods that often entangle different uncertainty sources, leading to unclear quantification. Their proposed ProvNeRF framework models per-point provenance, enriching the model with information on triangulation quality and enabling direct estimation of uncertainty associated with the image capturing process. This per-point probabilistic approach contrasts with previous deterministic methods, offering more nuanced uncertainty estimations. By leveraging the provenance field, ProvNeRF provides more accurate uncertainty maps, better aligning with depth error regions, ultimately leading to improved robustness and reliability in various applications of NeRFs.
Future Work & Limits#
The research paper’s ‘Future Work & Limits’ section would ideally delve into several crucial aspects. Extending ProvNeRF’s applicability to diverse NeRF architectures and 3D scene representations beyond the tested baselines is a key area. The current post-hoc optimization approach, while effective, introduces computational overhead; thus, exploring more efficient, integrated methods is critical. A thorough analysis of the impact of different latent function choices within ProvNeRF and exploring more sophisticated stochastic field models is also warranted. Addressing the limitations of the IMLE objective in functional spaces, perhaps through alternative probabilistic methods, and providing a comprehensive study of the algorithm’s sensitivity to various hyperparameters would enhance its robustness. Finally, further research should investigate the broader implications of per-point provenance modeling for downstream tasks such as uncertainty quantification, scene completion, and interactive manipulation, along with rigorous quantitative and qualitative evaluations to validate these improvements.
More visual insights#
More on figures
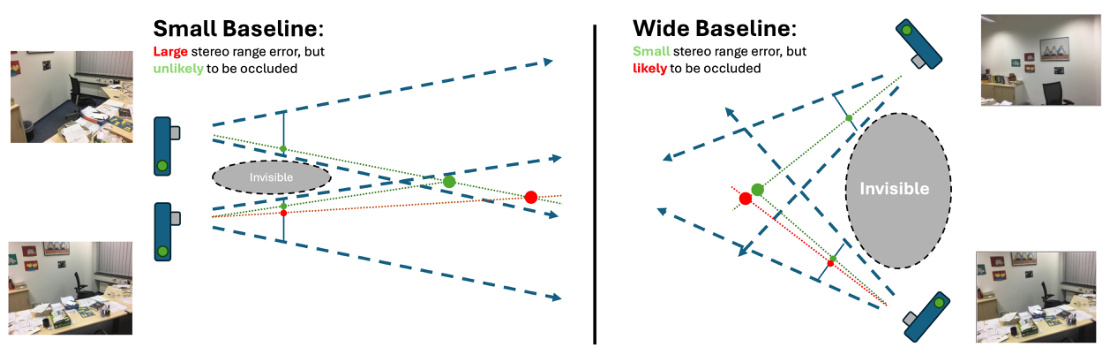
This figure illustrates the complex relationship between camera baseline distance and 3D reconstruction quality. A small baseline reduces occlusions but increases sensitivity to noise, resulting in large stereo range errors. Conversely, a wide baseline is more robust to noise but may omit hidden surfaces due to a larger invisible region.
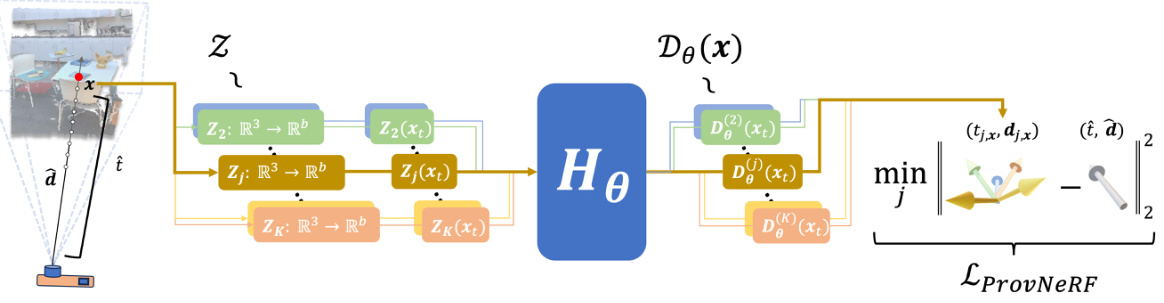
This figure illustrates the training pipeline of ProvNeRF. For each 3D point x, ProvNeRF samples K latent random functions from a distribution Z. These functions are then transformed by a learned transformation Hθ to produce K provenance samples D(j)(x), representing the likely locations from which point x is visible. The transformation Hθ is trained to minimize the LProvNeRF loss function (Eq. 9), which aims to match the generated samples with empirical provenance data. The process involves using distance-direction tuples to represent provenance samples and incorporates a minimization step to find the best match between model and empirical data.

This figure shows a qualitative comparison of novel view synthesis results between the proposed ProvNeRF method and the baseline SCADE method. The figure presents four pairs of images, each pair showing a different scene. The top row displays the results from SCADE, and the bottom row displays the results from ProvNeRF. The images illustrate that ProvNeRF effectively removes floating artifacts in the reconstructed scene, leading to a more refined and accurate representation of the environment. The yellow boxes highlight the areas where ProvNeRF significantly improves the scene reconstruction by removing these artifacts. The dashed red boxes highlight the test views used to evaluate the novel view synthesis results.
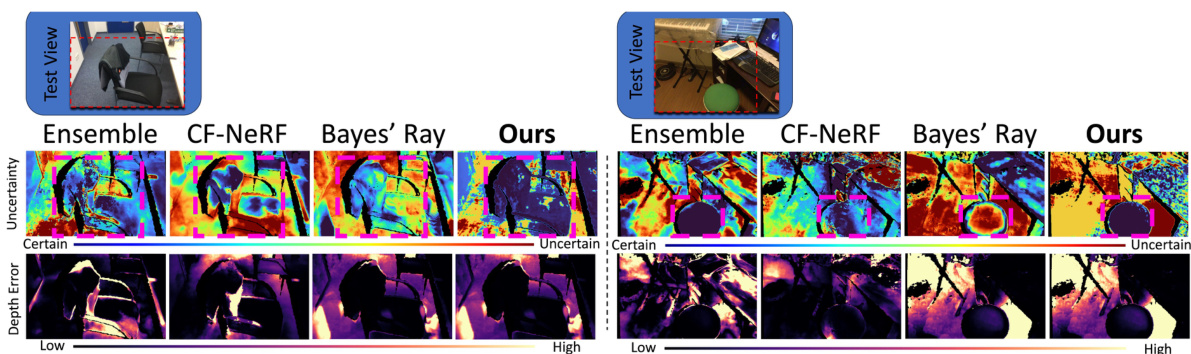
This figure presents a qualitative comparison of uncertainty maps generated by different methods, including the proposed approach. Two scenes are shown, each with uncertainty maps and depth error maps from various methods. The maps are color-coded to represent the degree of uncertainty and depth error. The goal is to demonstrate that the proposed method’s uncertainty estimates better correlate with depth errors.
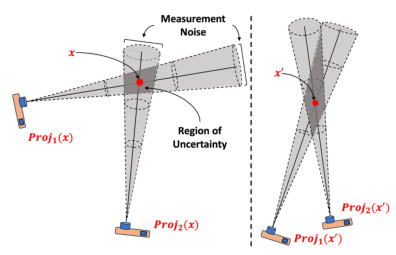
This figure illustrates the concept of triangulation uncertainty in multi-view geometry. The left panel shows two cameras viewing a 3D point (red dot) with a relatively wide baseline, resulting in a smaller region of uncertainty (grey cone). The right panel shows the same setup, but with a narrower baseline, resulting in a larger region of uncertainty. The caption highlights the relationship between the angle between the rays (baseline) and the resulting uncertainty.

This figure visualizes the learned provenance field by sampling 16 provenances at different locations in a test view of the Scannet scene. Each sample’s direction is represented by an arrow, colored according to its predicted visibility (red for high visibility, blue for low). The visualization demonstrates the model’s ability to predict multimodal provenance distributions at various scene points, capturing complex dependencies between camera locations and point visibility.

This figure compares uncertainty estimation results between the proposed method (ProvNeRF) and a baseline method (FisherRF) when applied to 3D Gaussian splatting (3DGS). It shows qualitative comparisons of uncertainty maps and depth error maps for two different scenes. The color scale represents the uncertainty level; areas of higher uncertainty should have higher depth errors. ProvNeRF’s uncertainty maps correlate better with depth error maps than FisherRF’s. A quantitative comparison (negative log-likelihood) shows ProvNeRF outperforms FisherRF, indicating more accurate uncertainty estimations.
More on tables

This ablation study analyzes the impact of different components of ProvNeRF on novel view synthesis performance, specifically focusing on the Scannet dataset. It compares the results of using a deterministic provenance field, a frustum check method, and the full ProvNeRF model. The metrics used to evaluate the performance are PSNR, SSIM, and LPIPS.
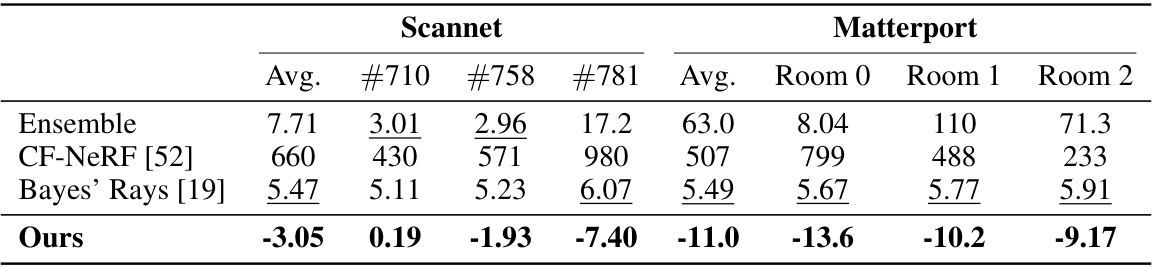
This table presents the negative log-likelihood (NLL) results for triangulation uncertainty evaluation using different methods: Ensemble, CF-NeRF, Bayes’ Rays, and the proposed ProvNeRF method. The results are shown for several scenes from the Scannet and Matterport3D datasets, offering a quantitative comparison of the uncertainty estimation performance across various approaches. Lower NLL indicates better uncertainty estimation.
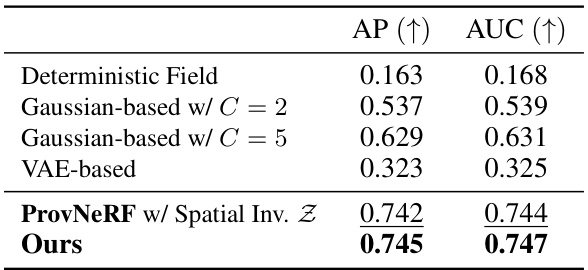
This ablation study analyzes the impact of different design choices in ProvNeRF on the average precision (AP) and area under the curve (AUC) metrics for provenance prediction. It compares a deterministic provenance field, Gaussian mixture models with different numbers of components (C), a VAE-based model, and the proposed ProvNeRF approach with and without spatial invariance in the latent function Z. The results demonstrate the superiority of the proposed ProvNeRF model over alternatives.
Full paper#















