↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Fine-tuning large language models (LLMs) for specialized tasks is computationally expensive and data-intensive. Existing data selection methods often struggle with data efficiency, especially for specialized domains, because they rely on large, computationally expensive models that generate representations for each training example. These methods are vulnerable to the quality of the training data and the computational cost of generating representations increases with model size.
The proposed method, SMALLTOLARGE (S2L), addresses these issues by training a small model to cluster training examples based on their loss trajectories. S2L selects a subset of data from these clusters, ensuring that the selected data is representative of the entire dataset. Experiments show that S2L significantly improves data efficiency in fine-tuning LLMs for mathematical problem-solving and clinical text summarization, achieving comparable or even better performance than training on the full dataset while using only a small fraction of the data. S2L also achieves superior data efficiency compared to other state-of-the-art data selection methods, and it is scalable to large models, using a reference model that is 100x smaller than the target model.
Key Takeaways#
Why does it matter?#
This paper is highly important for researchers working on large language models (LLMs) and data efficiency. It introduces a novel, scalable data selection method (S2L) that significantly reduces the training data needed for fine-tuning, which is a crucial challenge in the field. The results demonstrate substantial improvements in data efficiency across diverse domains, opening up new avenues for research on efficient LLM training and specialized domain adaptation.
Visual Insights#
This figure illustrates the limitations of existing data selection methods. Panel (a) shows that pre-trained models can effectively separate topics in natural language. However, panel (b) demonstrates that these methods struggle when fine-tuning data deviates from the pre-training distribution. Finally, panel (c) highlights the escalating computational cost of training a reference model as its size increases, making it impractical for large models.

This table presents a comparison of zero-shot accuracies achieved by different data selection methods (including SMALLTOLARGE (S2L)) when training with only 50K data points. The results are compared against the performance obtained by training on the full MathInstruct dataset. The comparison includes in-domain and out-of-domain datasets. The target model used is Phi-2 (2.7B). Note that Figure 4 uses the same settings, but employs the Pythia-410M model instead.
In-depth insights#
Small Model Loss#
The concept of “Small Model Loss” in the context of fine-tuning large language models (LLMs) is a crucial innovation. It leverages the training loss trajectories of a significantly smaller, computationally cheaper model to guide data selection for the much larger target model. This is highly significant because training a large LLM on a massive dataset is expensive, both in time and resources. Using a small model to identify valuable training examples is key. The strategy focuses on clustering data based on the similarity of their loss trajectories, which are assumed to correlate with gradient similarity during target model training. This theoretically grounded approach ensures that subsets selected from the loss trajectory clusters maintain bounded gradient error with respect to the full data. Therefore, the smaller model acts as a proxy for efficiently identifying data points crucial for the large model’s training, effectively achieving similar performance with far less data and computational overhead. The efficiency gains are substantial, allowing the method to outperform state-of-the-art data selection methods while proportionally reducing the overall computational cost. Scalability is also a strength, as the reference model can be orders of magnitude smaller than the target model.
Gradient Similarity#
The concept of ‘Gradient Similarity’ in the context of a research paper likely refers to the analysis of how similar the gradients are for different data points during the training of a machine learning model. Similar gradients suggest that these data points contribute similarly to the model’s learning process. This insight is valuable for data selection because it allows for the identification of redundant data points; selecting only a subset of similar gradient points would still capture the essence of the full dataset’s information, significantly improving data efficiency and reducing computational costs. The paper likely explores this similarity mathematically, potentially proving a bound on the error incurred by using a subset of data with similar gradients. The practical implication is that a smaller, representative dataset can achieve similar performance to a larger dataset, leading to faster training and reduced resource requirements. The effectiveness of this approach depends on the ability to accurately cluster data points based on gradient similarity. The research might have used a smaller model as a proxy to compute gradients, and thus the analysis might involve comparing loss trajectories or other metrics to evaluate the similarity. Finally, the paper may have demonstrated this approach’s success through empirical results on various tasks.
Scalable Data Select#
Scalable data selection methods for large language models (LLMs) are crucial for efficient fine-tuning, especially in specialized domains. A scalable approach must address the computational cost of processing large datasets. Training a smaller, proxy model to guide data selection for larger models is a key strategy. This approach leverages the smaller model’s loss trajectories to identify subsets of training data with similar gradients. This allows for significant reductions in training data while maintaining model accuracy and performance, addressing the critical issue of data efficiency. The approach should also incorporate methods for robust clustering of loss trajectories, and it must provide theoretical guarantees for the quality of the selected subset. Scalability also necessitates efficient methods for analyzing and selecting data from a large dataset; thus, clustering techniques are particularly helpful. Effective scalable data selection for LLMs involves balancing the tradeoff between computational cost and performance, and the method’s ability to be readily implemented across varying datasets and model architectures.
Math & Med Results#
A hypothetical section titled “Math & Med Results” would present the core findings of a study applying a novel data selection method to large language models (LLMs) in mathematical problem-solving and clinical text summarization. Significant improvements in data efficiency would be highlighted, demonstrating how the proposed method reduces the amount of training data needed while maintaining or even exceeding the performance of models trained on the full dataset. Specific metrics like accuracy, BLEU scores, and ROUGE-L would be reported for each domain, comparing the new method against various baselines. The results section would likely showcase the scalability and robustness of the method, indicating its effectiveness across different model sizes and domains. The discussion would likely delve into the reasons behind the improved performance, possibly citing the method’s ability to identify and utilize the most informative data points effectively. A quantitative analysis comparing the selected data subsets to the original datasets might be included, showing similarities in overall characteristics but also demonstrating a more focused and efficient selection.
Future Works#
Future work could explore extending SMALLTOLARGE (S2L) to other domains and tasks beyond mathematical problem-solving and clinical text summarization. Investigating the algorithm’s performance with different model architectures and sizes is crucial. A comprehensive analysis of the influence of hyperparameters, such as the number of clusters and the length of loss trajectories, on the final data selection and model performance needs to be performed. Theoretical analysis focusing on convergence rates and generalization bounds is recommended. Exploring the potential for integrating S2L with other data selection or augmentation techniques to further improve efficiency should be examined. Addressing the computational cost associated with large models and extensive datasets through efficient clustering methods or distributed computing paradigms would significantly enhance the algorithm’s scalability. Finally, evaluating the robustness of S2L to noisy or imbalanced datasets deserves attention.
More visual insights#
More on figures

This figure illustrates the limitations of existing data selection methods. Panel (a) shows that pre-trained models effectively separate topics in natural language. However, panel (b) demonstrates that these methods struggle when fine-tuning data deviates from the pre-training distribution. Finally, panel (c) highlights the significant increase in training time as model size increases, rendering these methods impractical for large models.
This figure illustrates the limitations of existing data selection methods for large language models (LLMs). Panel (a) shows that pre-trained models can effectively separate topics in natural language. However, panel (b) demonstrates that these methods struggle when fine-tuning data deviates from the pre-training distribution. Finally, panel (c) highlights the high computational cost of training a reference model, especially for large LLMs, making existing data selection methods prohibitively expensive.

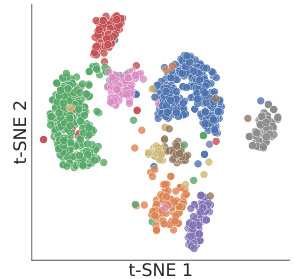
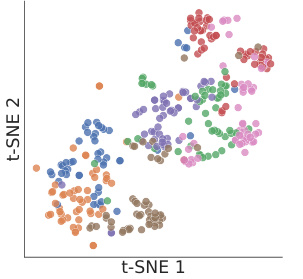
This figure shows a comparison of loss trajectories for examples within the same cluster versus those in different clusters. The left panel (2a) illustrates that examples within the same cluster exhibit highly similar loss trajectories during training, indicating similar gradient updates. The right panel (2b), in contrast, shows examples from different clusters, demonstrating significant differences in their loss trajectories over training iterations. This visual representation supports the paper’s claim that similar loss trajectories imply similar gradient behavior, which forms the basis for their data selection algorithm.

This figure shows two plots visualizing the loss trajectories of examples during training. (a) demonstrates examples clustered together, which exhibit almost identical loss trajectories across training iterations, highlighting the effectiveness of clustering similar examples together based on their loss. In contrast, (b) illustrates loss trajectories of examples in different clusters, demonstrating their dissimilarity and the rationale for selecting examples from a variety of clusters.

This figure compares the wall-clock time required for training the reference model and performing data selection using two different methods: Facility Location and S2L (the proposed method). The x-axis represents the method used, while the y-axis indicates the time in hours. The figure shows that S2L is significantly faster than Facility Location, requiring substantially less time for both training the reference model and selecting the data.
This figure compares the performance of S2L against several baseline data selection methods across various data sizes using the Pythia-410M model. It shows that S2L consistently outperforms baselines, particularly with smaller datasets, demonstrating improved data efficiency. The results are shown as relative accuracy compared to training on the full dataset, highlighting S2L’s superior performance even with a small fraction of the data.

This figure compares the distribution of the most common topic within clusters generated using two different methods: Loss Trajectories (the proposed method S2L) and Fully-finetuned Embeddings (a standard method). The x-axis represents the fraction of the most common topic in each cluster, and the y-axis shows the number of clusters. The figure demonstrates that S2L produces clusters with a higher concentration of a single topic than the Fully-finetuned Embeddings method. This suggests that S2L is more effective at grouping similar examples together during training.

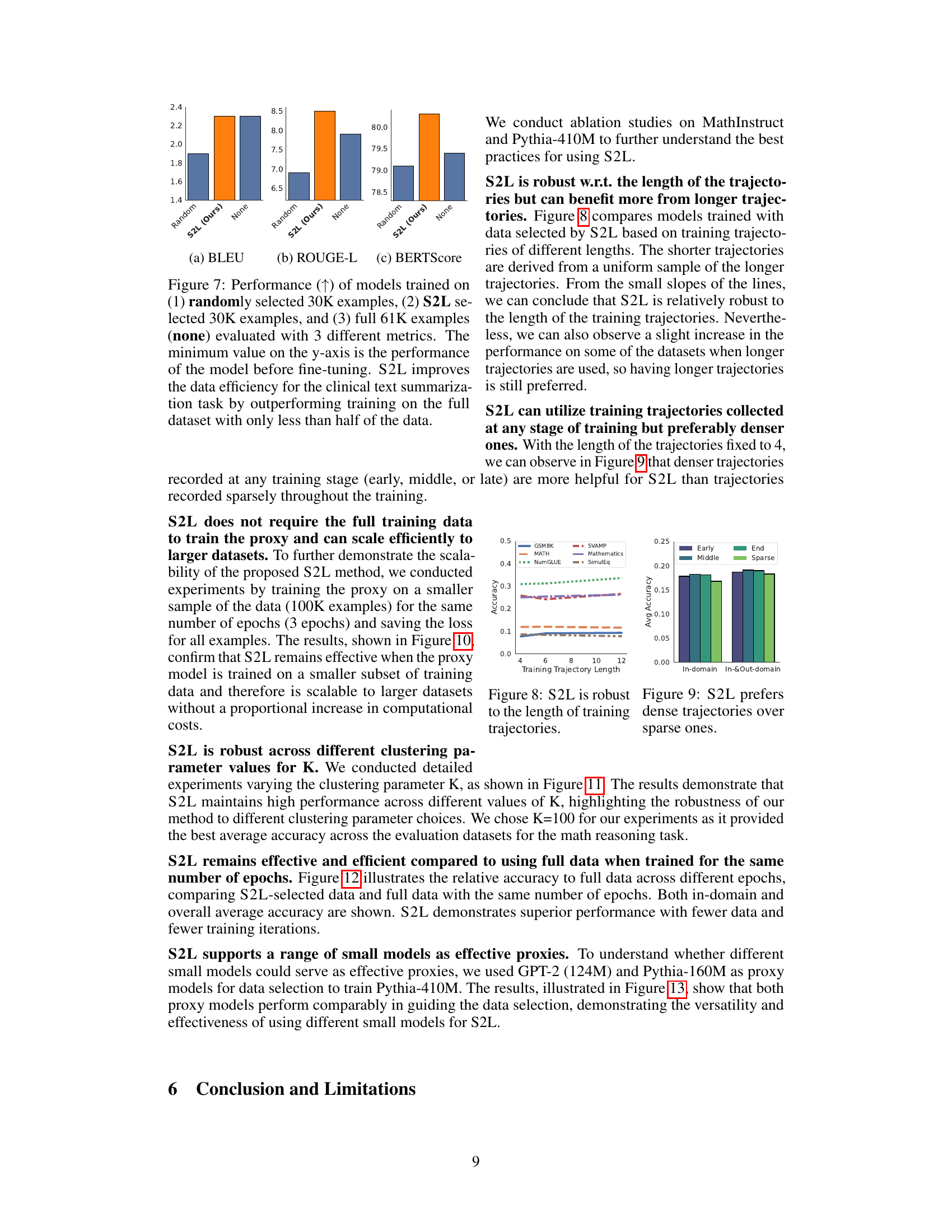
This figure compares the performance of models trained on randomly selected data, data selected using the SMALLTOLARGE (S2L) method, and the full dataset for clinical text summarization. The results are evaluated using three metrics: BLEU, ROUGE-L, and BERTScore. The figure shows that S2L achieves comparable or better performance than using the full dataset, while only using less than half the data, demonstrating the method’s improved data efficiency.
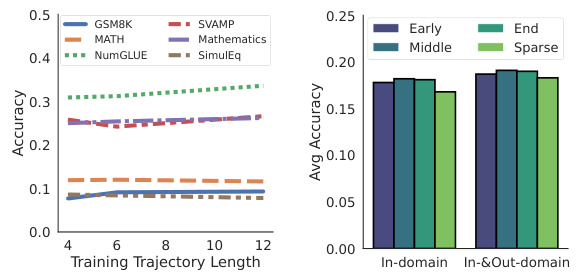
This figure shows the robustness of S2L to different lengths of training trajectories. The results show that while longer trajectories generally perform slightly better, S2L remains effective even with shorter trajectories, demonstrating its resilience to variations in data preprocessing or computational constraints.
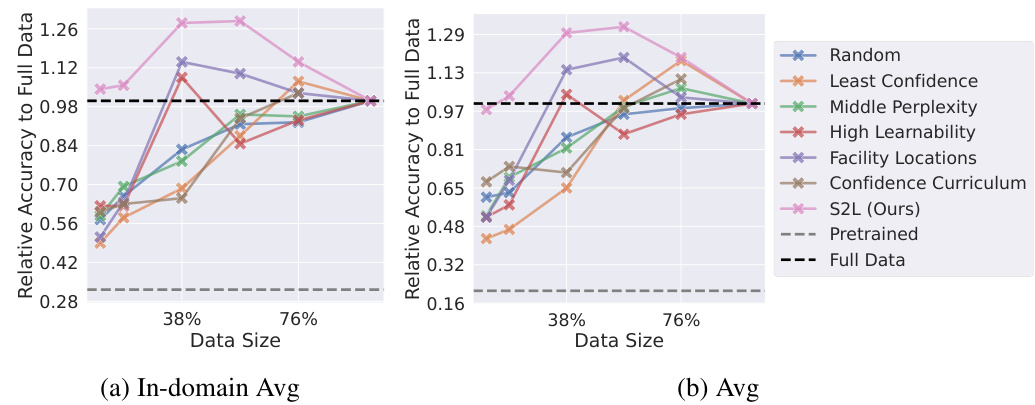
This figure displays the performance comparison across six datasets (three in-domain and three out-of-domain) using different data sizes (38% and 76% of the full dataset). It compares the performance of S2L against several baseline data selection methods. The results show that S2L consistently outperforms the baselines, even when using less training data, demonstrating its efficiency.
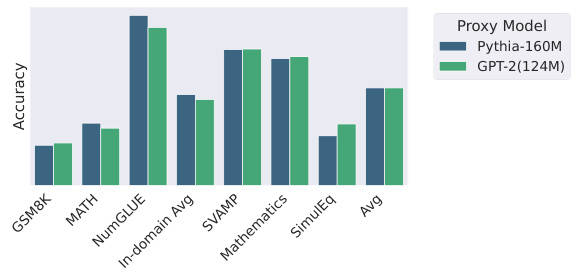
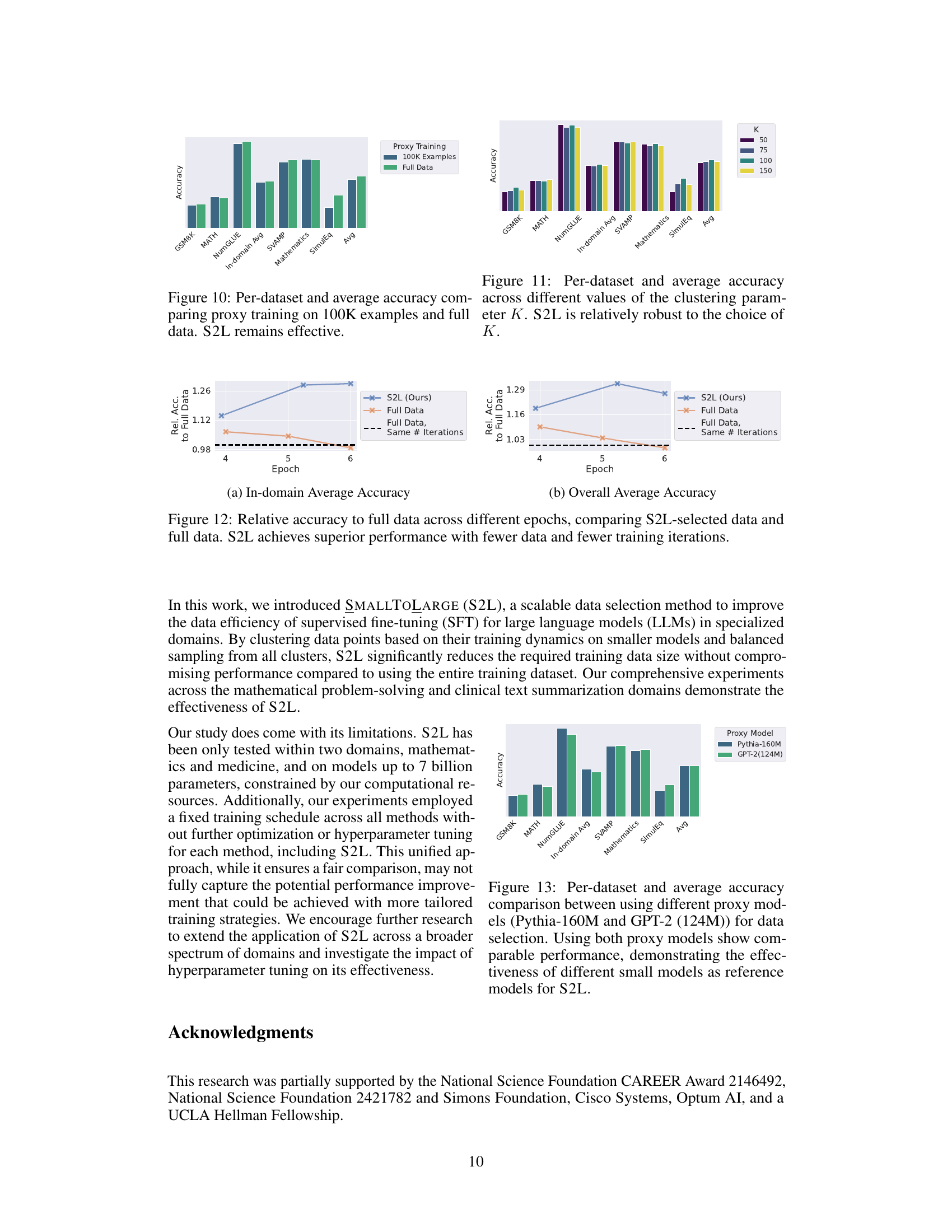
This figure compares the performance of S2L when using different small proxy models (Pythia-160M and GPT-2 (124M)). The results for six different datasets (GSM8K, MATH, NumGLUE, SVAMP, Mathematics, SimulEq) are shown individually, along with an average across all six. The comparison demonstrates the robustness of S2L to the choice of proxy model.

This figure compares the performance of different data selection methods (Random Sampling, Least Confidence, Middle Perplexity, High Learnability, Facility Locations, Confidence Curriculum, and SMALLTOLARGE) against training on the full dataset when using Pythia-410M model. The y-axis represents the relative accuracy to the full dataset, and the x-axis represents the proportion of the data used for training (38%, 76%). The results show that S2L significantly outperforms the other methods, especially with smaller datasets.

This figure shows the performance of different data selection methods on the Pythia-410M model for mathematical reasoning, comparing in-domain and out-of-domain datasets. It demonstrates that the proposed S2L method significantly outperforms other methods, particularly when the training data is limited. The y-axis represents relative accuracy compared to using the full dataset, and the x-axis shows the fraction of the training data used.

This figure compares the topic distribution of the original MathInstruct dataset and the topic distributions of subsets of data selected by the SMALLTOLARGE (S2L) algorithm for different data sizes (30K, 50K, 100K). It shows that S2L tends to prioritize simpler topics (like pre-algebra) while ensuring a more even representation of all topics compared to a random selection or the full dataset.

This figure illustrates the limitations of existing data selection methods. Part (a) shows that pretrained models can effectively separate topics in natural language. However, part (b) demonstrates that these methods struggle when fine-tuning data deviates from the pretraining distribution. Finally, part (c) highlights the high computational cost of training a reference model, especially for large models, making existing methods impractical.
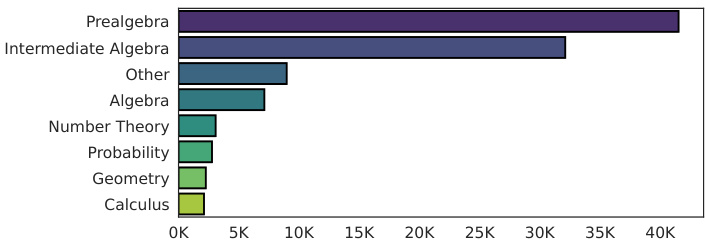
This figure shows a comparison of topic distributions in the MathInstruct dataset. The bar chart (a) displays the original topic distribution within the full dataset. Charts (b) through (d) show the distributions of topics after data selection using the SMALLTOLARGE (S2L) method with different data budget sizes (30K, 50K, and 100K data points). The S2L method is shown to shift the emphasis from more advanced topics (like calculus) towards easier topics (like pre-algebra), resulting in a more balanced distribution across topics.
More on tables

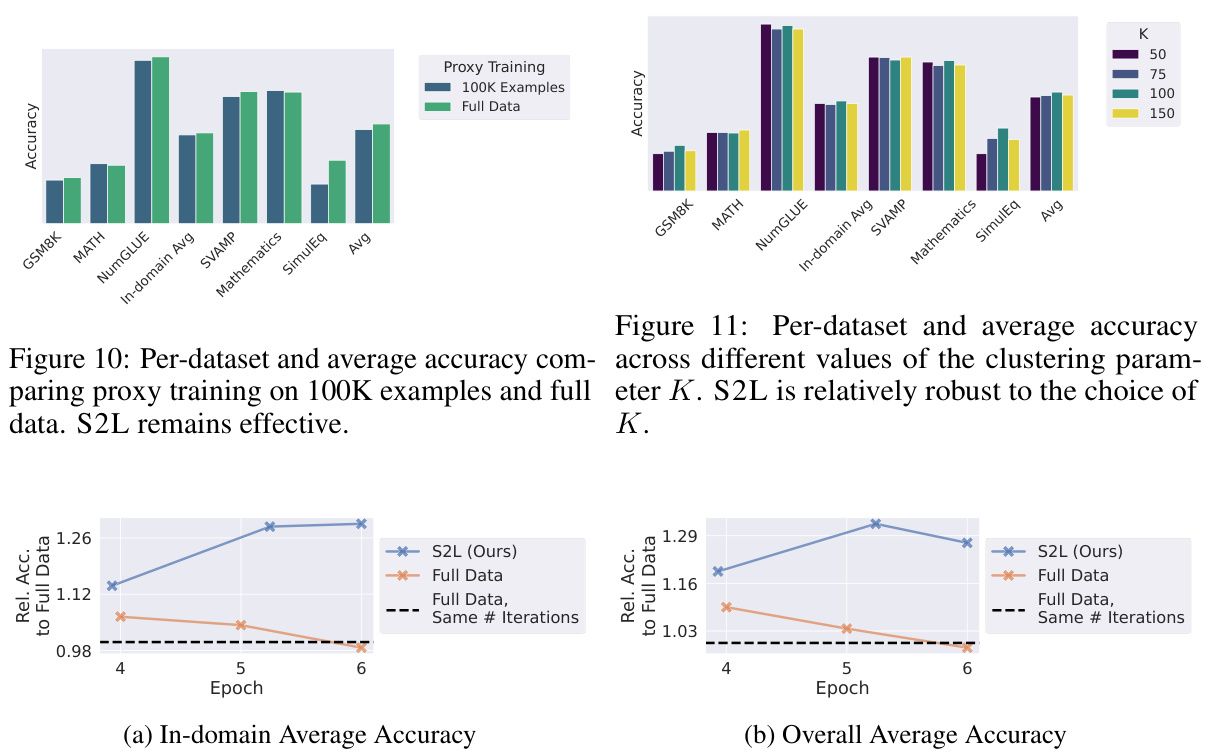
This table presents the zero-shot accuracies achieved by training the target model on 50% of the data selected by S2L, compared to the full data training. The number of training epochs is kept constant in both cases. The results show that S2L achieves comparable performance using significantly less data and training time compared to the full dataset.

This table presents the zero-shot accuracy results for different data selection methods on the MathInstruct dataset, using the Pythia model. It compares the performance of S2L against baselines using only 50,000 data points, matching the computation time of training on the full dataset. The table shows that S2L significantly outperforms other data selection techniques and even achieves better results than training on the entire dataset.
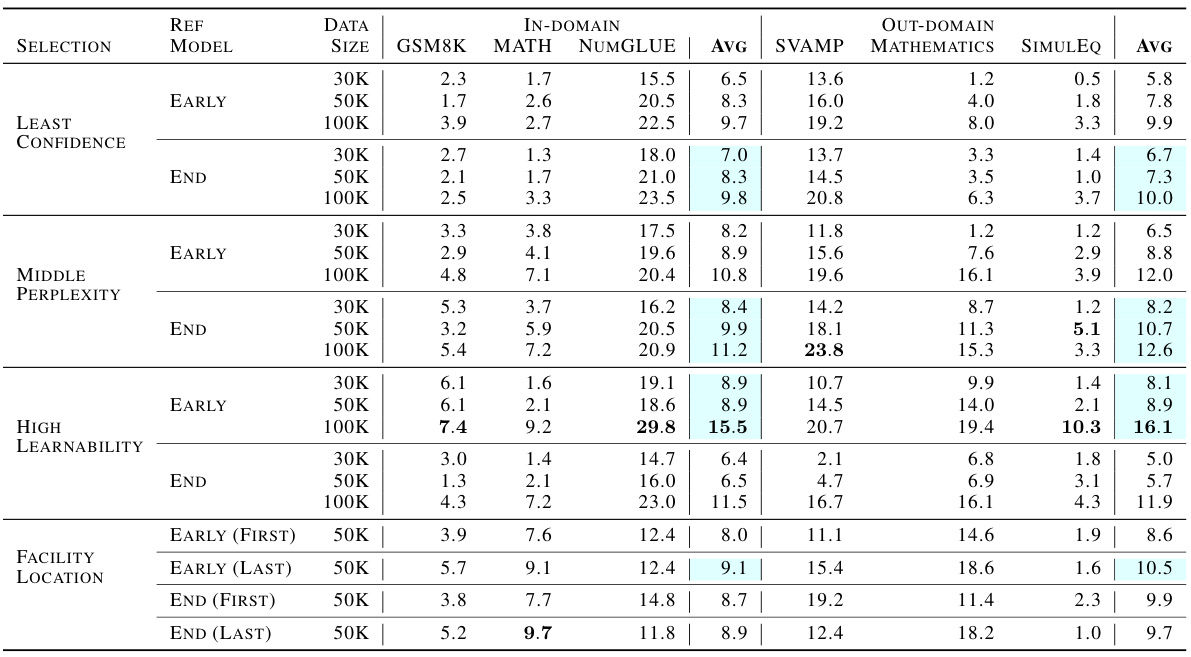
This table presents a detailed comparison of different data selection methods, using various reference models (early and late fine-tuning checkpoints). It shows the performance of each method on several metrics across different data budget sizes (30K, 50K, and 100K examples). The best performing method for each setting is highlighted to help with selecting the best reference model for subsequent data selection.
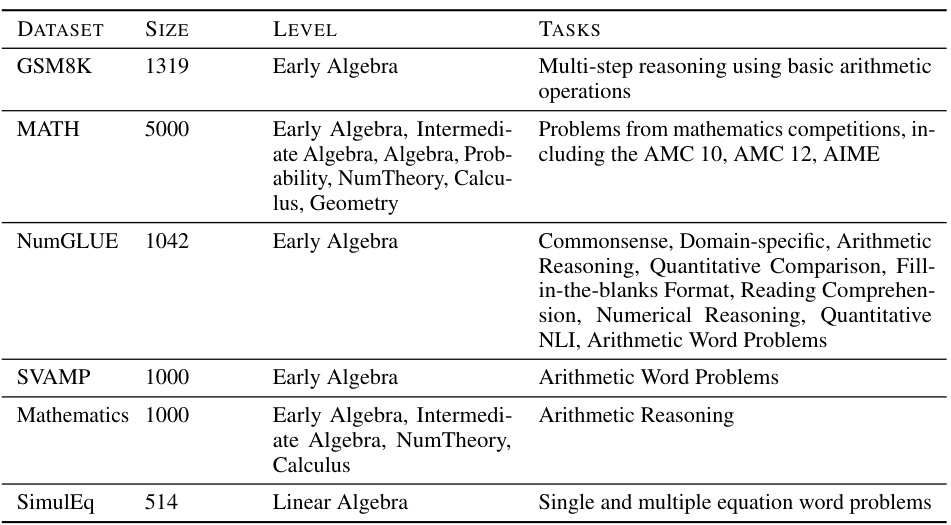
This table details the characteristics of six different datasets used to evaluate the performance of mathematical reasoning models. Each dataset is described by its name, size (number of questions), the level of mathematical knowledge required (e.g., Early Algebra, Calculus), and the types of tasks involved (e.g., multi-step reasoning, arithmetic word problems). This information helps to understand the scope and difficulty of the evaluation benchmarks.
Full paper#