↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Generative Adversarial Imitation Learning (GAIL), a prominent method in reinforcement learning for training agents from expert demonstrations, suffers from instability and brittleness. The core issue lies in the reward function used for policy learning often being unstable and noisy, which is generated by GAIL’s discriminator. This results in unreliable and inefficient training.
The proposed Diffusion-Reward Adversarial Imitation Learning (DRAIL) tackles this problem by incorporating diffusion models into GAIL to enhance the discriminator. This refined discriminator provides smoother and more informative rewards, leading to significantly improved policy learning. Extensive experiments across various tasks (navigation, manipulation, locomotion) demonstrate DRAIL’s superior performance in terms of stability, generalizability, and data efficiency compared to existing methods. DRAIL’s novel approach to reward generation makes a substantial contribution to the field of imitation learning.
Key Takeaways#
Why does it matter?#
This paper is important because it proposes a novel solution to the instability issues in Generative Adversarial Imitation Learning (GAIL), a widely used technique in reinforcement learning. By integrating diffusion models, it improves the robustness and smoothness of reward functions, leading to more reliable and efficient policy learning. This offers a significant advancement in imitation learning and opens avenues for more robust and generalizable AI agents.
Visual Insights#
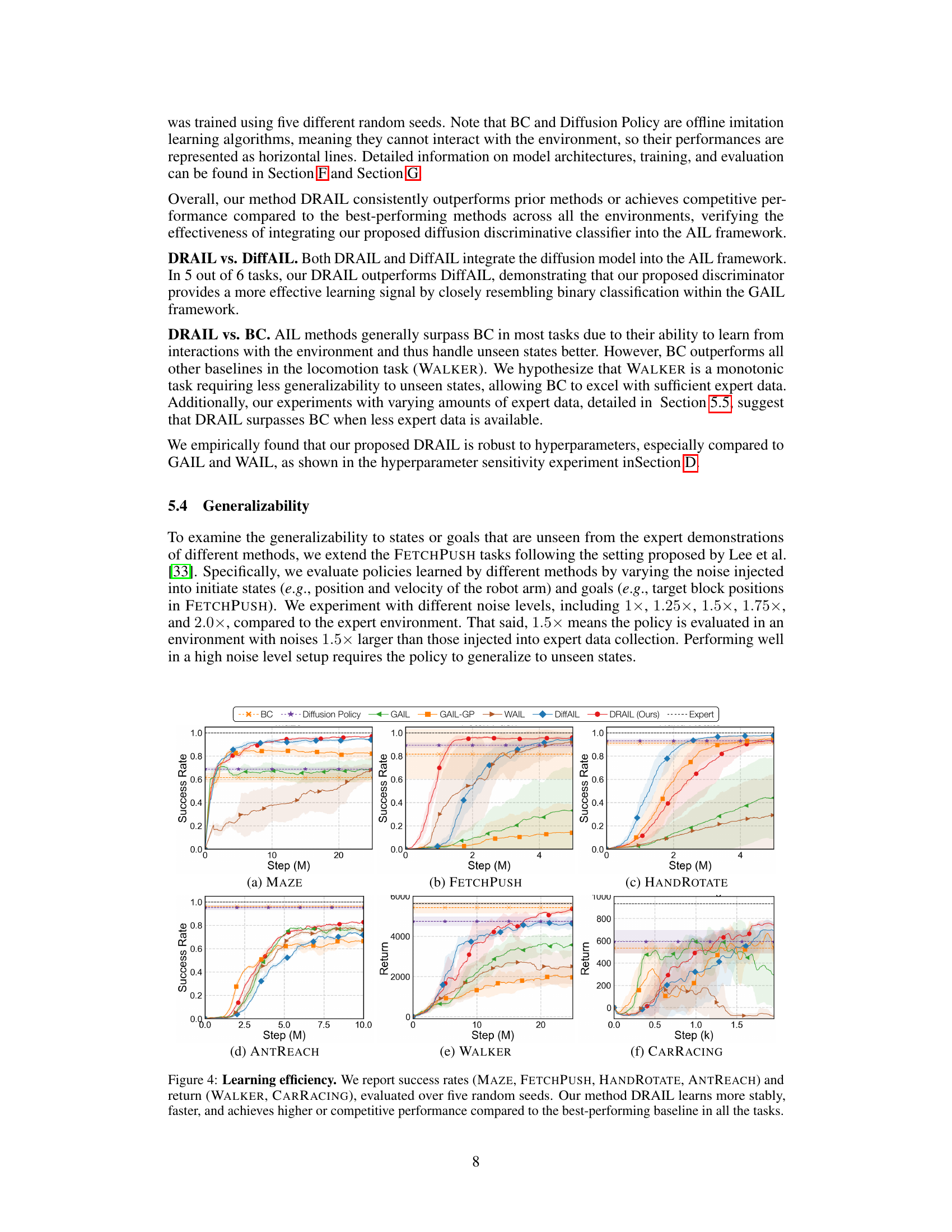
This figure illustrates the denoising diffusion probabilistic model. It shows how the forward diffusion process adds Gaussian noise to the data points over time steps, transforming them into an isotropic Gaussian distribution. The reverse diffusion process, trained by a diffusion model, learns to predict and remove the added noise, step-by-step, eventually reconstructing the original data point from the noisy version. This model is used as a key component in the proposed method DRAIL for generating improved reward functions.

This table presents a comprehensive summary of the final performance metrics achieved by various imitation learning methods across different continuous control tasks. The results encompass both main experiments and generalization experiments under varied conditions. Metrics such as success rate and return are reported, providing a quantitative comparison of the algorithms’ effectiveness in different scenarios and varying amounts of training data. The table allows for an in-depth assessment of each algorithm’s robustness, generalization capability, and data efficiency.
In-depth insights#
Diffusion Models in AIL#
Integrating diffusion models into adversarial imitation learning (AIL) offers a promising avenue for enhancing the robustness and stability of the training process. Diffusion models’ ability to smoothly generate data by gradually removing noise can help create smoother reward functions, mitigating the instability issues often encountered in traditional AIL methods. This smoother reward landscape can lead to more stable policy learning and improved sample efficiency. Furthermore, the use of diffusion models can potentially improve the generalizability of learned policies by enabling the model to learn from a wider variety of state-action distributions. However, challenges remain in effectively leveraging the power of diffusion models within the adversarial framework, particularly in efficiently balancing the training of the generator and discriminator. Careful consideration of computational costs and the choice of appropriate diffusion model architectures are also crucial for successful implementation. Future research should explore various architectural designs and training strategies to fully harness the potential of diffusion models in advancing the field of AIL.
DRAIL Framework#
The DRAIL framework presents a novel approach to adversarial imitation learning by integrating diffusion models. This integration enhances the discriminator’s ability to distinguish between expert and agent trajectories, leading to more robust and smoother reward functions. Instead of directly predicting rewards, DRAIL utilizes a diffusion discriminative classifier, a conditional diffusion model that efficiently classifies state-action pairs as either expert or agent. The classifier’s output provides a refined reward signal for policy learning, improving stability and efficiency. The use of a conditional model addresses limitations of previous methods that relied on unconditional diffusion models, leading to a more effective and stable training process. Moreover, the framework shows strong empirical results across diverse continuous control domains, highlighting its effectiveness and generalizability in various scenarios.
Reward Function Design#
Effective reward function design is crucial for successful reinforcement learning, especially in imitation learning scenarios where explicit rewards are unavailable. A poorly designed reward function can lead to suboptimal or unsafe policies, highlighting the need for careful consideration. Reward shaping techniques are often employed to guide the agent towards desirable behavior. Adversarial methods, like Generative Adversarial Imitation Learning (GAIL), frame the problem as a game between a generator (policy) and a discriminator (reward function), creating a more robust reward signal. However, GAIL can suffer from instability and mode collapse. Integrating diffusion models offers a potential solution, enabling the creation of smoother and more robust reward landscapes. The choice of reward function representation (e.g., hand-designed, learned, or a combination) significantly impacts performance. Data efficiency is also a critical concern. A well-designed reward function reduces the amount of data required for training, leading to a more efficient learning process. Therefore, a sophisticated approach to reward function design considers reward shaping, adversarial training, diffusion modeling, representation selection, and data efficiency to achieve successful imitation learning.
Generalization Analysis#
A robust generalization analysis is crucial for evaluating the real-world applicability of any machine learning model, especially in imitation learning. It assesses how well the learned policy performs on unseen data or tasks, going beyond simple training set accuracy. Key aspects of this analysis would involve testing the model’s performance across diverse scenarios, systematically varying factors such as state distributions, environmental dynamics, or task goals, beyond those observed in the training data. The results should quantify the performance degradation as these factors deviate from the training distribution and reveal the model’s sensitivity to changes. Ideally, this analysis should leverage rigorous statistical measures and visualization techniques to reveal insights into the model’s robustness. Comparing its generalization capabilities to existing baselines is essential for determining its true novelty and contribution. A thorough investigation of generalization performance is key to building trust and confidence in the reliability of learned policies in real-world applications, where the environment inevitably deviates from idealized training conditions.
Future Work#
The paper’s ‘Future Work’ section presents exciting avenues for development. Extending DRAIL to image-based robotic tasks in real-world settings is crucial for demonstrating practical applicability beyond simulated environments. Investigating DRAIL’s performance in diverse, complex domains beyond those tested will reveal its true generalizability. Exploring alternative divergence measures and distance metrics, such as Wasserstein distance or f-divergences, might improve training stability and robustness. Finally, mitigating potential biases arising from the expert demonstrations is a key ethical consideration, necessitating future work on ensuring fairness and preventing the reinforcement of undesirable behaviours. Addressing these aspects would significantly enhance DRAIL’s effectiveness and reliability.
More visual insights#
More on figures

This figure illustrates the architecture of the Diffusion-Reward Adversarial Imitation Learning (DRAIL) framework. Panel (a) shows how a diffusion discriminative classifier (Dφ) is trained to distinguish between expert and agent state-action pairs using a diffusion model (φ). The classifier learns to output a value close to 1 for expert data and 0 for agent data. Panel (b) shows how a policy (πθ) is trained to maximize the diffusion reward (r), which is calculated based on the output of the diffusion discriminative classifier. The reward incentivizes the policy to produce state-action pairs similar to those of the expert.

This figure shows the six different environments used in the paper’s experiments. Each subfigure illustrates a different task: navigation in a maze, robotic arm manipulation (pushing and picking), dexterous hand manipulation (in-hand rotation), quadruped locomotion (ant reaching), bipedal locomotion (walker), and image-based car racing. The tasks vary in complexity and dimensionality.
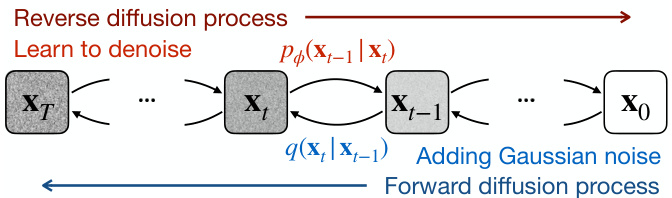
This figure shows the success rate and return of DRAIL and several baseline algorithms across six different continuous control tasks. The x-axis represents the number of environment steps, and the y-axis represents either the success rate (for MAZE, FETCHPUSH, HANDROTATE, and ANTREACH) or the return (for WALKER and CARRACING). DRAIL consistently outperforms or is competitive with the best baseline method across all tasks.

This figure shows the success rate of different imitation learning methods in the FETCHPUSH task under various levels of noise added to the initial states and goal locations. The x-axis represents the number of steps, and the y-axis represents the success rate. The different lines represent different methods: BC, Diffusion Policy, GAIL, GAIL-GP, WAIL, DiffAIL, DRAIL, and Expert. The shaded area around each line represents the standard deviation across three random seeds. The results show that DRAIL outperforms other methods in terms of success rate, especially under high noise levels.
This figure shows the learning curves of DRAIL and various baseline methods across six different continuous control tasks. The y-axis represents either success rate (for the navigation, manipulation, and reaching tasks) or cumulative return (for the locomotion and racing tasks). The x-axis represents the number of environment steps. DRAIL consistently outperforms or matches the best-performing baseline method across all tasks, highlighting its improved learning efficiency and stability.

This figure visualizes the learned reward functions of GAIL and DRAIL in a simple sine wave environment. Panel (a) shows the expert’s discontinuous sine wave function. Panel (b) shows the reward function learned by GAIL, demonstrating overfitting and a narrow reward distribution. Panel (c) shows the reward function learned by DRAIL; it’s smoother and has a broader distribution, indicating better generalization.
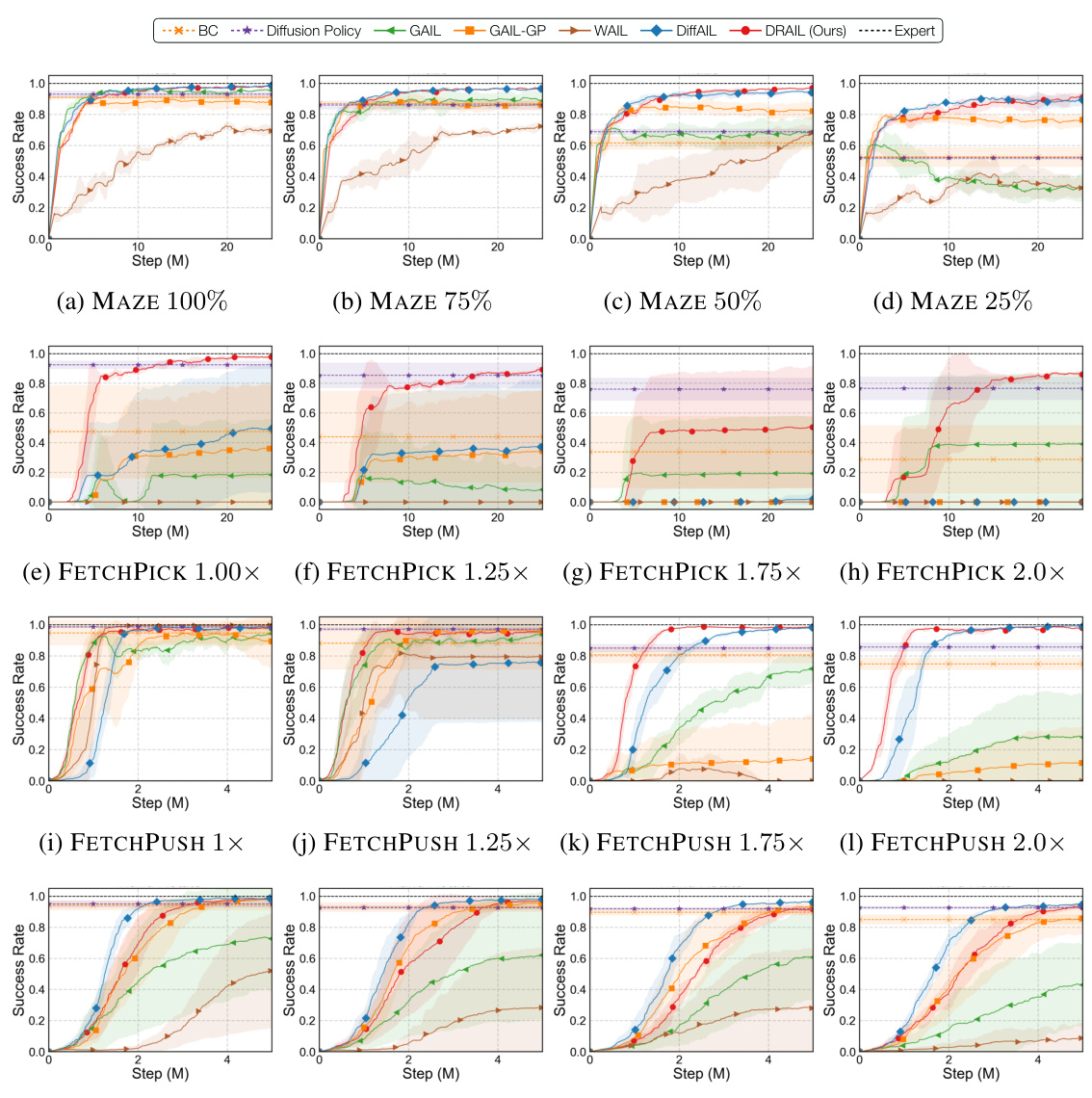
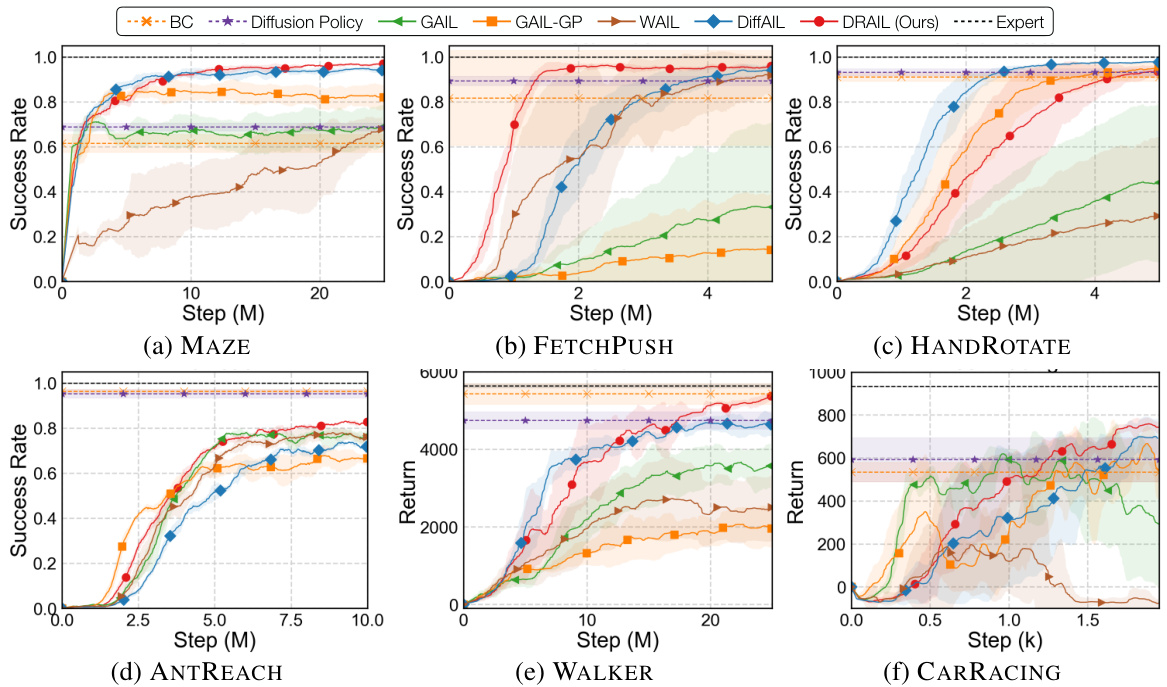
This figure displays the success rates of different imitation learning algorithms across six tasks, under varying conditions. The top row shows results from the MAZE task with different proportions of training data used. The following rows show results from FETCHPICK and FETCHPUSH, which involve pushing and picking tasks with varying levels of noise in initial conditions and target positions. The general trend is that DRAIL (the authors’ method) consistently outperforms other algorithms, showcasing its robustness and ability to generalize well to unseen situations.

This figure displays the results of a hyperparameter sensitivity experiment conducted on the DRAIL model within the MAZE environment. Two subfigures show the impact of varying the discriminator learning rate (a) and the policy learning rate (b) on the model’s success rate. Multiple lines represent different scaling factors (0.2x, 0.5x, 1x, 2x, 5x) applied to the baseline learning rate. The consistent success rate across the varying learning rates demonstrates the robustness of DRAIL to different hyperparameter choices.
More on tables

This table presents a comprehensive summary of the final performance metrics achieved by different imitation learning methods across various tasks and experimental settings. The results include success rates (for tasks with binary success/failure outcomes) and average returns (for tasks with continuous reward signals). Results are shown for the main experiments, generalization experiments (with varying levels of noise and data coverage), and data efficiency experiments (with different amounts of expert data). The table allows for direct comparison of DRAIL against baselines across different scenarios.
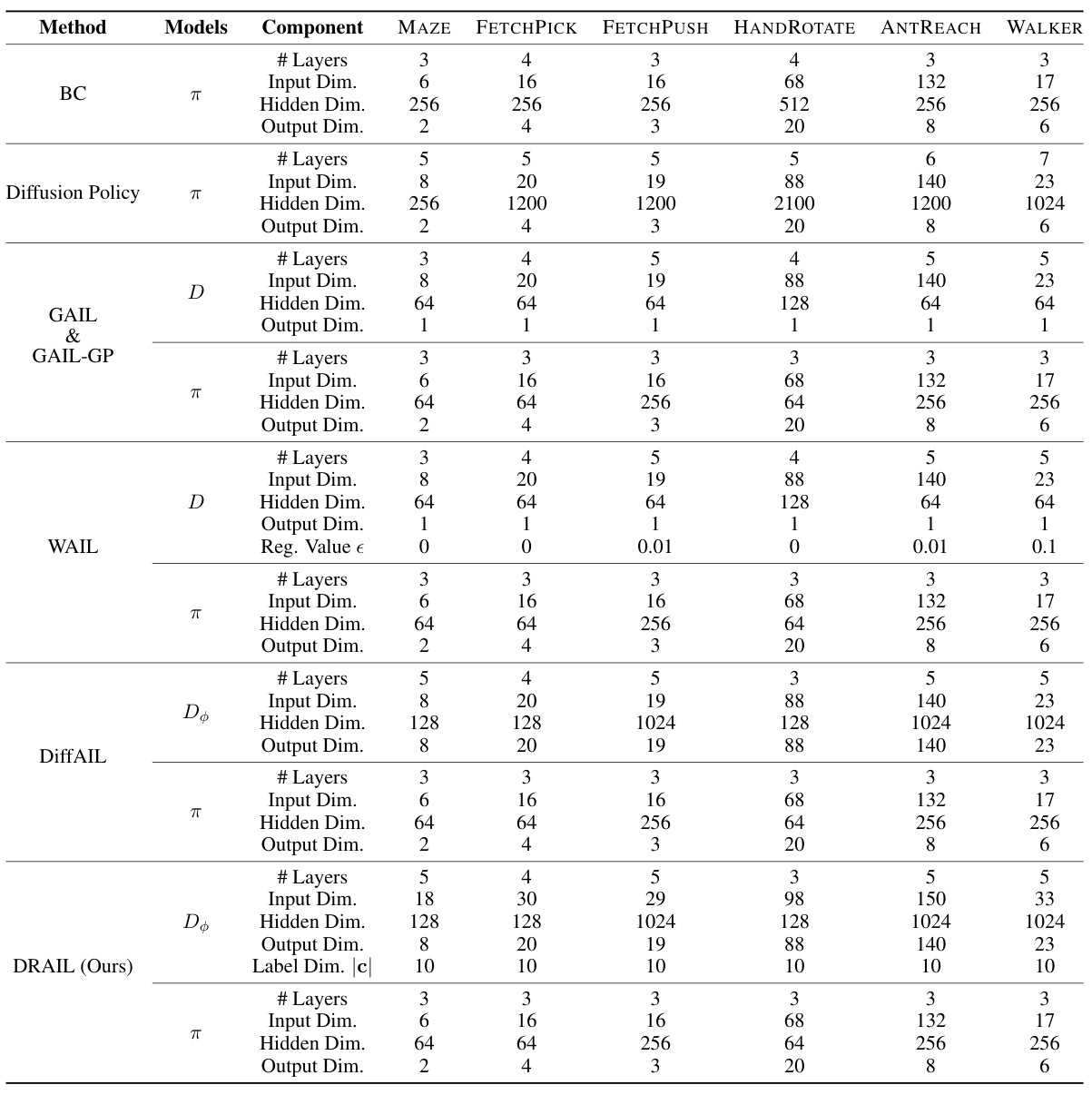
This table details the architecture of the neural networks used for policies and discriminators in different methods (BC, Diffusion Policy, GAIL, GAIL-GP, WAIL, DiffAIL, and DRAIL) across six tasks. For each method, it lists the number of layers, input dimensions, hidden dimensions, and output dimensions of the respective networks. It also specifies additional parameters like the regularization value (e) for WAIL and the label dimension (c) for DRAIL. The table provides a comprehensive overview of the network configurations for each imitation learning method.
This table details the architecture of the models used in the experiments. It shows the number of layers, input dimensions, hidden layer dimensions, and output dimensions for different components (policy and discriminator) of various imitation learning methods (BC, Diffusion Policy, GAIL, GAIL-GP, WAIL, DiffAIL, DRAIL) across six different tasks. Note that it differentiates between the multilayer perceptron (MLP) used in some methods and the diffusion model used in others.

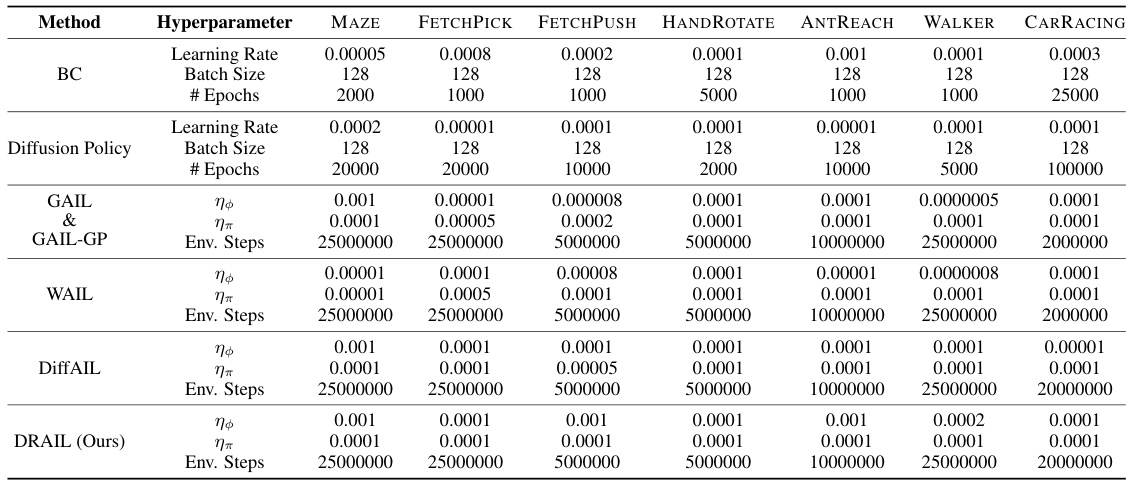
This table lists the hyperparameters used for Proximal Policy Optimization (PPO) during the training process for different tasks in the imitation learning experiments. It includes the clipping range (epsilon), discount factor (gamma), generalized advantage estimation (GAE) parameter (lambda), value function coefficient, and entropy coefficient. These hyperparameters influence the stability and performance of the PPO algorithm in various continuous control environments.
Full paper#