↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Hyperparameter optimization (HPO) is vital for iterative machine learning models, but existing methods often overlook model training uncertainty. This leads to suboptimal performance, as promising candidates might be prematurely discarded. The paper highlights the significant performance limitations caused by ignoring uncertainty in iterative machine learning model training, particularly in the early stages.
This paper introduces a novel UQ-guided scheme to address this issue. By quantifying model uncertainty and incorporating it into the candidate selection and budget allocation process, the UQ-guided scheme enhances existing HPO techniques. Experimental results demonstrate substantial performance improvements, achieving over 50% reduction in accuracy regret and exploration time compared to traditional methods. This work emphasizes the importance of considering model uncertainty for effective HPO.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on hyperparameter optimization (HPO), particularly for iterative machine learning models. It introduces a novel uncertainty-aware approach, addressing a critical gap in existing HPO methods. The proposed UQ-guided scheme significantly improves HPO efficiency and performance, reducing regret by 21-55% and exploration time by 30-75%. This work opens new avenues for more efficient and robust HPO techniques.
Visual Insights#
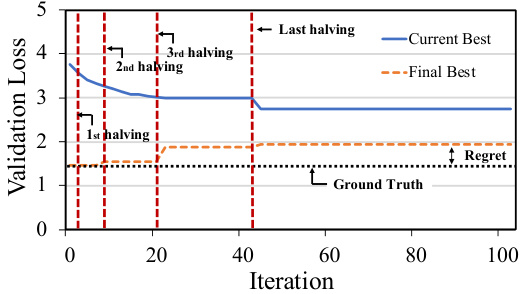
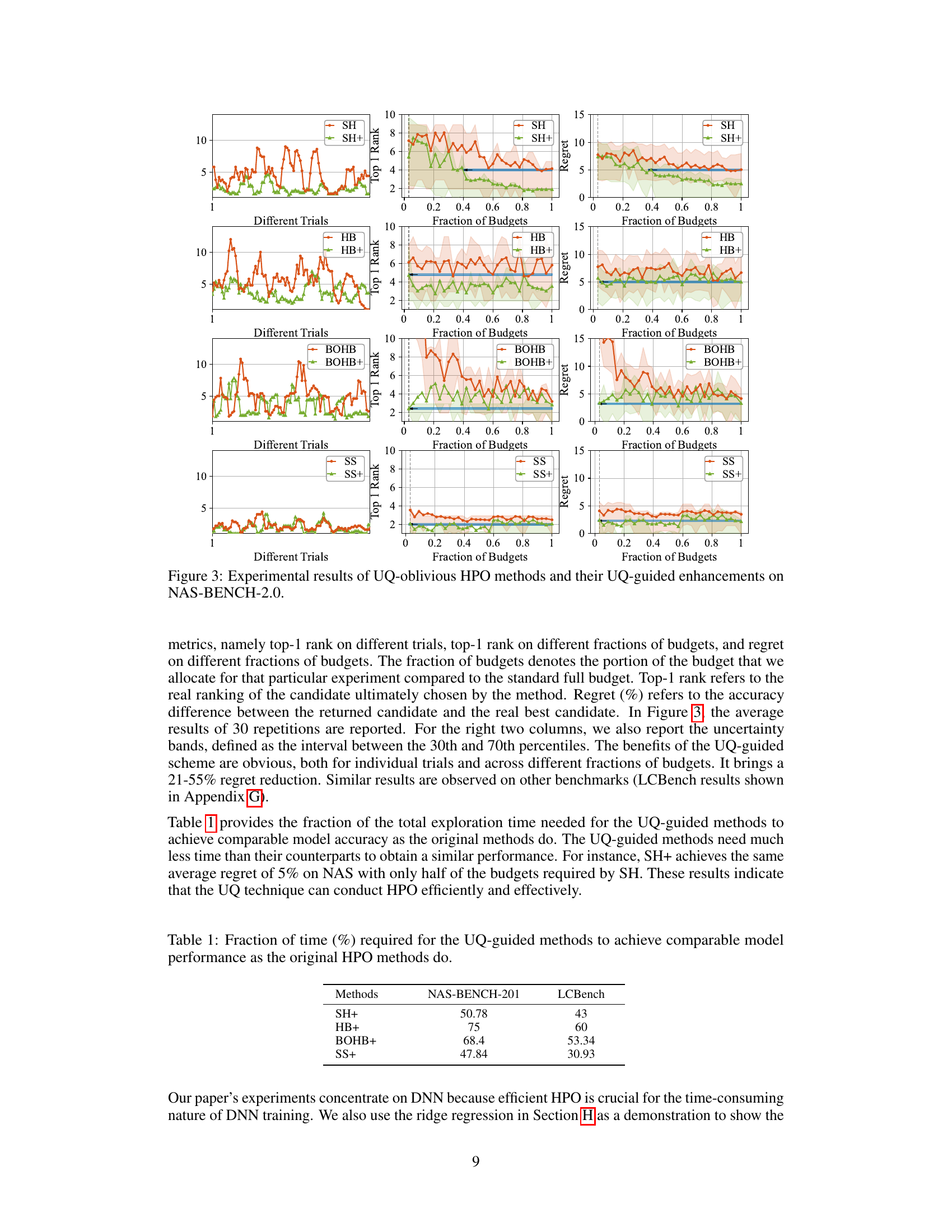
This figure demonstrates how model uncertainty negatively affects hyperparameter optimization (HPO) using the Successive Halving (SH) method on the NAS-BENCH-2.0 benchmark. The blue line shows the best validation loss observed so far during the optimization process, while the orange dashed line represents the true best validation loss after training has fully converged. The red dashed lines show the points at which SH discards half of the candidates. The figure highlights that SH, relying only on current validation loss, prematurely discards candidates that would ultimately have performed well due to uncertainty during the initial training stages. This leads to increased regret (the difference between the true best and the selected model). Further details are provided in Section 4.1 and Appendix F of the paper.
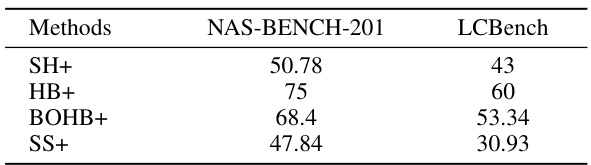
This table presents the efficiency gains achieved by the UQ-guided HPO methods compared to their original counterparts. It shows the percentage of time each UQ-guided method (SH+, HB+, BOHB+, SS+) needed to reach a comparable model performance level as its original UQ-oblivious version (SH, HB, BOHB, SS) on two benchmark datasets (NAS-BENCH-201 and LCBench). Lower percentages indicate better efficiency.
In-depth insights#
UQ-HPO: A New Scheme#
UQ-HPO, a novel scheme, addresses the critical gap in hyperparameter optimization (HPO) by explicitly incorporating model uncertainty. Unlike traditional HPO methods that solely rely on observed performance, UQ-HPO quantifies and leverages uncertainty to guide the search process. This is achieved by constructing a probabilistic model that approximates the statistical effects of discarding candidates prematurely. The scheme then uses this probabilistic model to drive candidate selection and budget allocation. By quantifying uncertainty, UQ-HPO effectively addresses the issue of prematurely discarding promising candidates that exhibit poor performance in the initial training stages due to inherent model uncertainty. The scheme is designed to be versatile and can be integrated into various existing HPO methods. Empirical results across multiple benchmarks showcase the effectiveness of UQ-HPO, delivering substantial performance gains, exceeding 50% improvement in terms of accuracy and exploration time. This innovative approach demonstrates the power of uncertainty-aware HPO and its potential to significantly enhance the efficiency and effectiveness of hyperparameter tuning.
Uncertainty Quantification#
The concept of ‘Uncertainty Quantification’ in the context of hyperparameter optimization (HPO) for iterative learners is crucial because it directly addresses the inherent randomness and variability in the training process of machine learning models. Traditional HPO methods often neglect this uncertainty, leading to suboptimal results. A key contribution of the paper is to introduce a principled framework for quantifying this uncertainty. Model uncertainty, stemming from limited data and model limitations, is specifically targeted. This is cleverly done by constructing a probabilistic model to capture the stochastic nature of model training, allowing for more informed decision-making during the HPO process. This probabilistic model is used to estimate both the mean and variance of the validation loss, which are then used to guide both the selection of promising candidate hyperparameter configurations and the allocation of computational resources. The impact of model uncertainty on the selection of candidates is explicitly shown, demonstrating how ignoring uncertainty can lead to the premature discarding of configurations that eventually perform well. The use of confidence curves provides a visually intuitive way to understand the probabilistic assessment of candidate configurations and to make informed decisions about which candidates should be considered for further evaluation and how much computational resource should be devoted to them.
Experimental Results#
The heading ‘Experimental Results’ in a research paper warrants a thorough analysis. It should present a clear and concise summary of findings, going beyond simply stating the results. A strong section will include visualizations (charts, graphs) to aid in understanding. Statistical significance should be clearly reported using appropriate measures like p-values, confidence intervals, and effect sizes. The discussion should compare results to those of prior work, highlighting key differences and similarities. It’s essential to discuss limitations and potential biases in the methodology which could influence the interpretation of results. Reproducibility should be prioritized; sufficient detail regarding experimental setup, data, and parameters must be given so that others may replicate the study. Finally, a thoughtful concluding statement reflecting on the overall implications of the results and future directions of research is crucial to maximizing the impact of the paper.
Theoretical Analysis#
A theoretical analysis section in a research paper would delve into the mathematical underpinnings and provide rigorous justification for the proposed method. It would likely involve formal proofs of key claims, demonstrating the correctness and efficiency of the uncertainty quantification (UQ) guided scheme. This could involve establishing bounds on the probability of selecting the best candidate, demonstrating convergence properties of the approach, and potentially comparing its theoretical performance to existing UQ-oblivious methods. Key assumptions made throughout the analysis would be clearly stated, along with a discussion of their implications and potential limitations. The theoretical analysis should aim to provide a comprehensive understanding of the approach’s behavior beyond empirical observations, offering a robust framework for understanding its strengths and limitations. Furthermore, it may provide valuable insights for future research and improvement, suggesting areas for further investigation and refinement. The analysis would ideally include the derivation of key equations, the mathematical foundations upon which the UQ-guided scheme is built, providing a comprehensive and transparent account of the model’s behavior and performance.
Future Work#
Future research directions stemming from this work could explore several promising avenues. Extending the UQ-guided scheme to a broader range of iterative learners beyond DNNs and ridge regression is crucial to demonstrate its general applicability and effectiveness. This would involve adapting the uncertainty quantification methods and the decision-making process to the specific characteristics of other iterative learning algorithms. Investigating different uncertainty quantification techniques beyond the lightweight method used in this paper is another avenue of exploration. More sophisticated methods might improve accuracy and robustness, especially for complex models and challenging datasets. A theoretical analysis of the impact of various hyperparameter optimization methods in conjunction with the UQ-guided scheme could yield valuable insights into the optimal strategies for different scenarios and model types. This could encompass a comparative analysis of the trade-offs between exploration and exploitation under uncertainty. Finally, developing a more comprehensive understanding of the interplay between model uncertainty and hyperparameter optimization in various settings (e.g., different data distributions, model architectures, and training strategies) could lead to more sophisticated and adaptive HPO algorithms.
More visual insights#
More on figures

This figure illustrates the UQ-guided scheme, a method for enhancing the Successive Halving algorithm by incorporating uncertainty quantification. It shows how the scheme uses a probabilistic model to estimate the uncertainty in model training, constructs a confidence curve to assess the probability of selecting the best candidate, and employs a discarding mechanism to eliminate less promising candidates while optimizing resource allocation across multiple rounds.
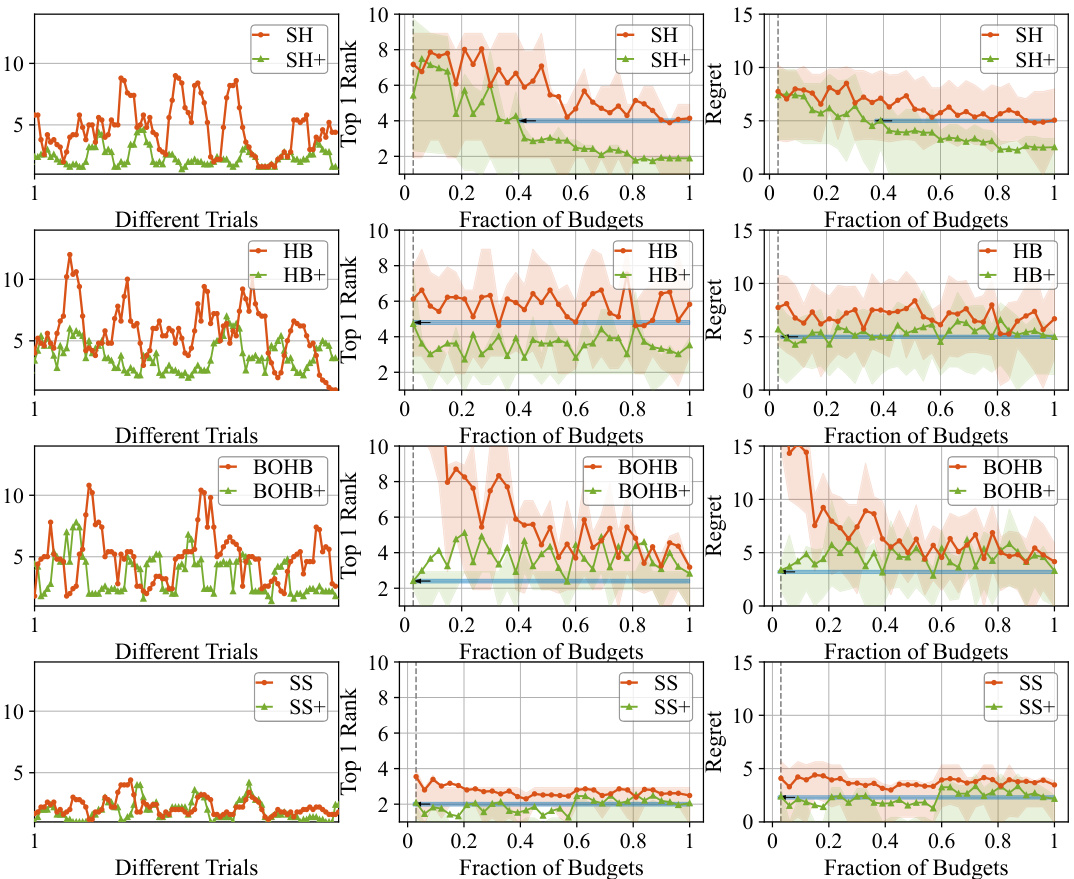
This figure presents the experimental results comparing the performance of UQ-oblivious HPO methods (original methods) against their UQ-guided enhancements (methods enhanced with the proposed UQ-guided scheme). The experiment was conducted on NAS-BENCH-201. Three performance metrics are shown for each method: Top-1 Rank on different trials, Top-1 Rank on different fractions of budgets, and Regret on different fractions of budgets. The results demonstrate that the UQ-guided enhancements consistently achieve lower regret and improved Top-1 Rank across various budget fractions, highlighting the effectiveness of incorporating uncertainty quantification into HPO.

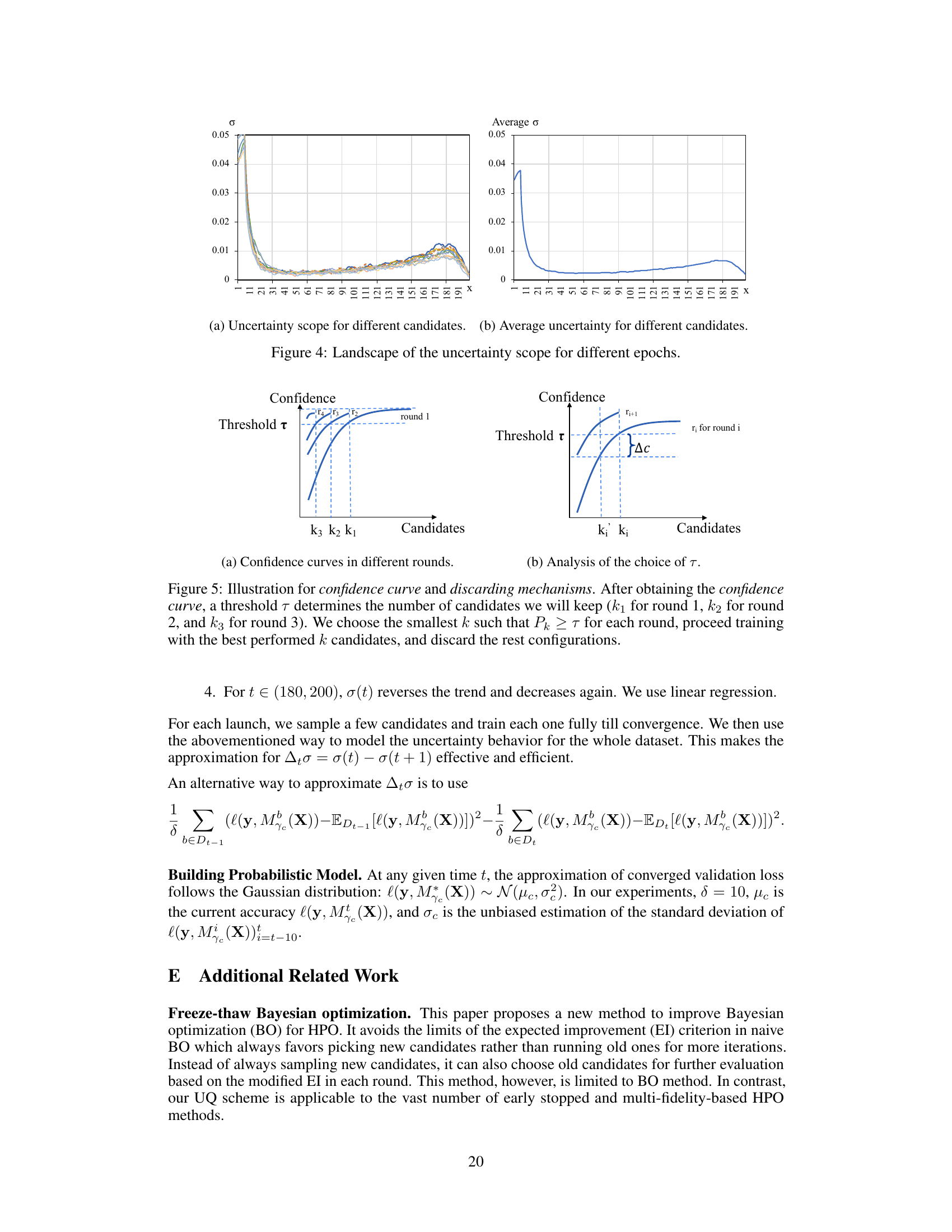
This figure visualizes the model uncertainty over training epochs. The left subplot displays the uncertainty (σ) for individual candidates, showing varying trends and magnitudes. The right subplot shows the average uncertainty across all candidates, illustrating an overall trend of initially high uncertainty that decreases, then slightly increases again during later training stages.

This figure illustrates the process of using the confidence curve to determine how many candidates to keep for further training in each round of the Hyperparameter Optimization (HPO). The confidence curve shows the probability that the best candidate is among the top k candidates. A threshold, τ, is set; any candidates below this threshold for a given round are discarded.

This figure illustrates the concept of a confidence curve and how it’s used in the UQ-guided scheme for discarding candidates in each round of the HPO process. The confidence curve shows the probability that the best candidate is among the top k candidates. A threshold (τ) is set, and the algorithm selects the smallest k that exceeds this threshold. This approach balances exploration and exploitation by dynamically adjusting the number of candidates retained in each round.

This figure shows the experimental results of comparing UQ-oblivious HPO methods and their UQ-guided enhancements on NAS-BENCH-201. It presents three different metrics: Top-1 Rank on different trials, Top-1 Rank on different fractions of budgets, and Regret on different fractions of budgets. The x-axis represents the fraction of budgets used, and the y-axis represents the metric being measured. The results demonstrate the improvements achieved by the UQ-guided enhancements across different trials and budget fractions, showcasing a significant reduction in regret.

The figure presents the experimental results comparing the performance of UQ-oblivious HPO methods (SH, HB, BOHB, SS) against their UQ-guided counterparts (SH+, HB+, BOHB+, SS+). Three key metrics are shown across different trials and fractions of the budget: Top-1 rank (the actual ranking of the selected candidate), fraction of budgets used, and regret (accuracy difference between the chosen candidate and the actual best candidate). The UQ-guided methods consistently demonstrate significant improvements in regret reduction (21-55%) and reduced exploration time (30-75%).
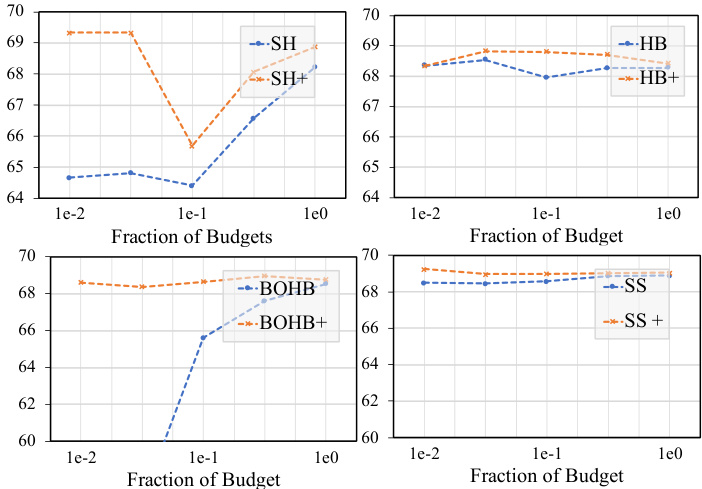
The figure presents a comparison of the performance of five different hyperparameter optimization (HPO) methods with and without the UQ-guided scheme on the NAS-BENCH-2.0 benchmark. Each method is evaluated using three metrics: Top-1 Rank (accuracy of the best candidate selected by the method), Regret (performance difference between the selected candidate and the true best candidate), and fraction of budgets used (proportion of training budget utilized). The results illustrate that UQ-guided versions consistently outperform their UQ-oblivious counterparts across all three metrics, demonstrating the effectiveness of the proposed UQ-guided scheme.

This figure presents the experimental results comparing the performance of UQ-oblivious and UQ-guided HPO methods on the NAS-BENCH-2.0 benchmark. It shows three metrics: Top-1 Rank (across different trials and budget fractions), and Regret (the accuracy difference between the chosen candidate and the best candidate). The results demonstrate that the UQ-guided enhancements significantly improve performance, showing a 21-55% reduction in regret and achieving comparable accuracy with a fraction of the original methods’ budget.

This figure displays the experimental results of comparing the UQ-oblivious HPO methods and their UQ-guided enhancements on the NAS-BENCH-2.0 benchmark. It shows three metrics across different trials and fractions of the budget: Top-1 rank, regret, and the fraction of budgets. The results demonstrate the improvements achieved by the UQ-guided enhancements in terms of reducing regret (accuracy difference between returned candidate and the actual best candidate) and improving top-1 rank accuracy. The uncertainty bands (30th and 70th percentiles) are also shown, highlighting the robustness of the UQ-guided approach.
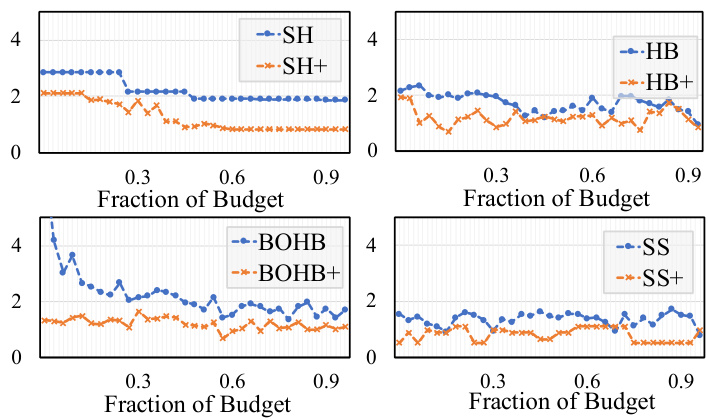
This figure presents the experimental results comparing the performance of UQ-oblivious HPO methods (SH, HB, BOHB, SS) against their UQ-guided counterparts (SH+, HB+, BOHB+, SS+). The results are shown for NAS-BENCH-2.0 across three metrics: Top-1 Rank (performance of the best candidate selected by each method), Regret (difference in performance between the selected candidate and the actual best candidate), and Fraction of Budgets (the proportion of the total budget used). The UQ-guided methods consistently demonstrate improved performance across all three metrics and different budget fractions, highlighting the benefit of incorporating uncertainty quantification into the HPO process.
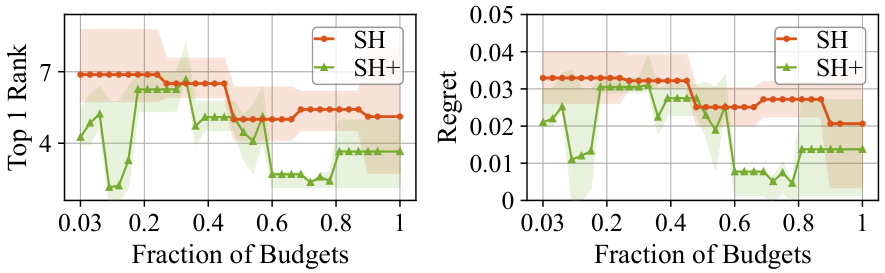
This figure presents the results of experiments comparing the performance of standard Successive Halving (SH) and the proposed uncertainty-quantification guided SH+ method for hyperparameter optimization using ridge regression. Two key metrics are shown: Top-1 Rank (the ranking of the best hyperparameter configuration found by each method) and Regret (a measure of the performance difference between the best configuration found and the true best configuration). The x-axis represents the fraction of the total budget used. The results demonstrate that SH+ consistently outperforms SH across different budget fractions, achieving both better Top-1 Rank and lower Regret, showcasing the effectiveness of incorporating uncertainty quantification into hyperparameter optimization.
Full paper#