TL;DR#
Reinforcement learning (RL) faces challenges in balancing exploration and exploitation, especially when explicit action-value functions are unavailable. Existing methods often lack theoretical guarantees or struggle with infinite state spaces. Policy Mirror Descent (PMD), a powerful method for sequential decision making, is not directly applicable to RL due to its reliance on these functions.
This paper addresses this by introducing POWR, an RL algorithm that uses conditional mean embeddings to learn a world model of the environment. Leveraging operator theory, POWR derives a closed-form expression for the action-value function, combining this with PMD for policy optimization. The authors prove convergence rates for POWR and demonstrate its effectiveness in finite and infinite state settings.
Key Takeaways#
Why does it matter?#
This paper is crucial for reinforcement learning (RL) researchers because it bridges the gap between theoretical optimality and practical applicability. By introducing POWR, a novel RL algorithm, it offers a closed-form solution for action-value functions, enabling efficient and theoretically sound policy optimization. This approach is particularly significant for infinite state-space settings, which are often challenging for conventional RL methods. The provided convergence rate analysis and empirical validation further enhance its appeal.
Visual Insights#

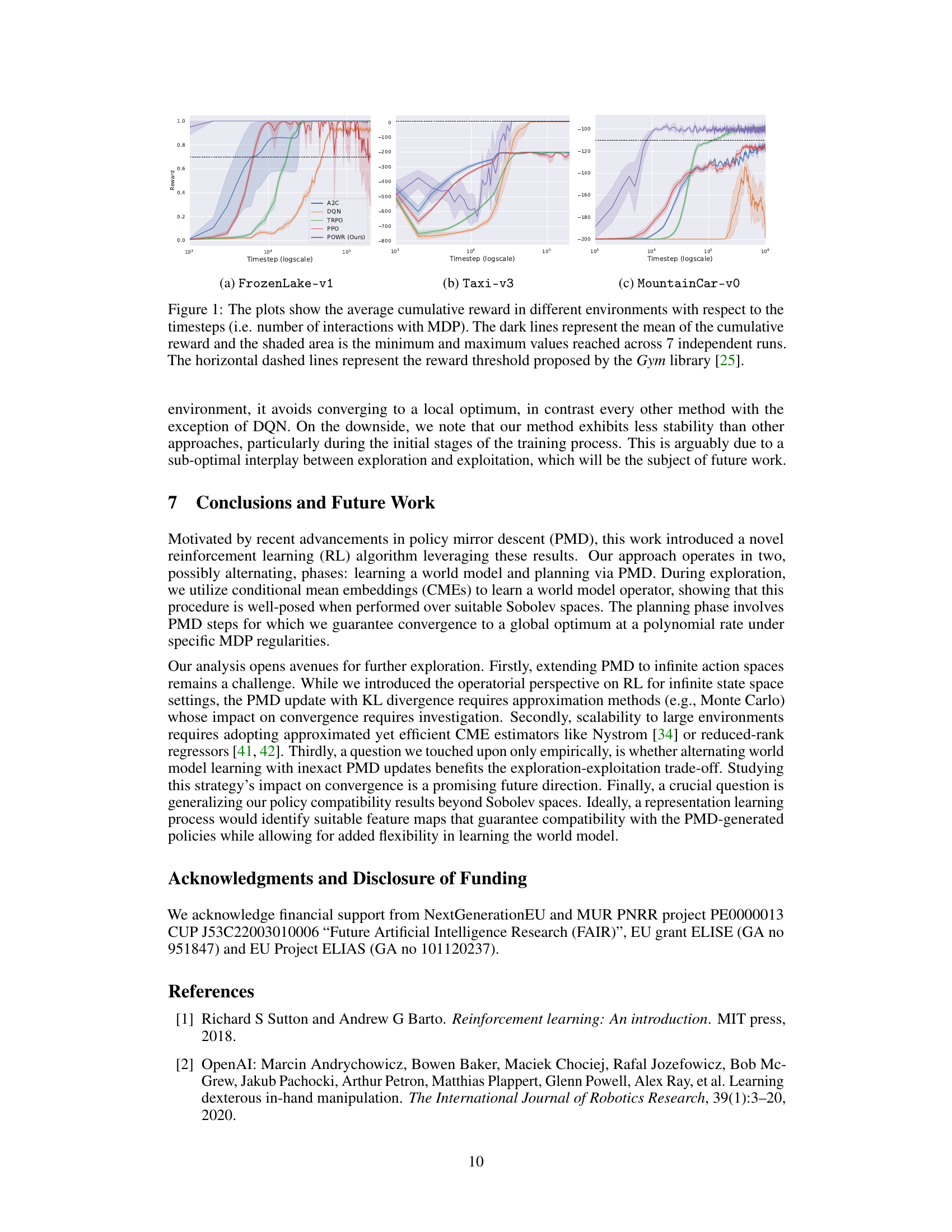
🔼 This figure compares the performance of the POWR algorithm to several baselines (A2C, DQN, TRPO, PPO) across three different Gym environments: FrozenLake-v1, Taxi-v3, and MountainCar-v0. The x-axis represents the number of timesteps (interactions with the environment), while the y-axis shows the cumulative reward. Shaded regions indicate the minimum and maximum rewards across seven independent runs. Horizontal dashed lines mark the reward thresholds defined in the Gym library. The figure demonstrates that POWR achieves higher cumulative rewards within a similar or fewer number of timesteps compared to the baselines.
read the caption
Figure 1: The plots show the average cumulative reward in different environments with respect to the timesteps (i.e. number of interactions with MDP). The dark lines represent the mean of the cumulative reward and the shaded area is the minimum and maximum values reached across 7 independent runs. The horizontal dashed lines represent the reward threshold proposed by the Gym library [25].
Full paper#