Neural Isometries: Taming Transformations for Equivariant ML

kCabCEhQWv

Thomas Mitchel et el.

TL;DR
#

Many real-world tasks involve complex symmetries that are difficult to model analytically. Existing geometric deep learning methods often require handcrafted architectures tailored to specific symmetries, limiting their generalizability. This paper aims to overcome these limitations by learning a latent space where these complex symmetries are simplified into tractable isometric maps.

The proposed framework, Neural Isometries, uses an autoencoder to map observations to a latent space. A key contribution is regularizing the latent space to preserve inner products and commute with learned operators, ensuring that geometrically related observations have isometrically related encodings in the latent space. This allows for simple equivariant networks to be used effectively in the latent space, achieving comparable results to complex handcrafted methods. Experiments demonstrate the approach’s effectiveness on various tasks including image classification with unknown homographies and robust camera pose estimation directly from latent space maps.

Key Takeaways
#

Why does it matter?
#

This paper is crucial for researchers in geometric deep learning and 3D vision. It introduces a novel, architecture-agnostic approach to handle complex symmetries, which is a major challenge in the field. The method’s ability to learn robust camera poses directly from latent space transformations opens exciting avenues for self-supervised learning and 3D scene understanding. The presented framework also provides an important step toward building equivariant models for unknown and difficult transformations.

Visual Insights
#

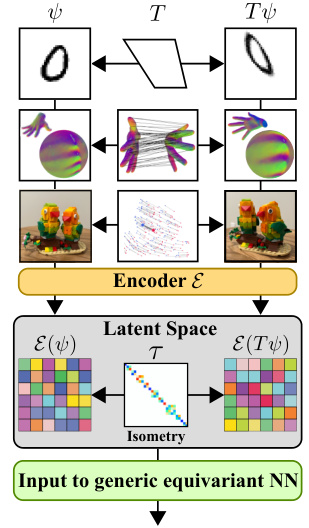
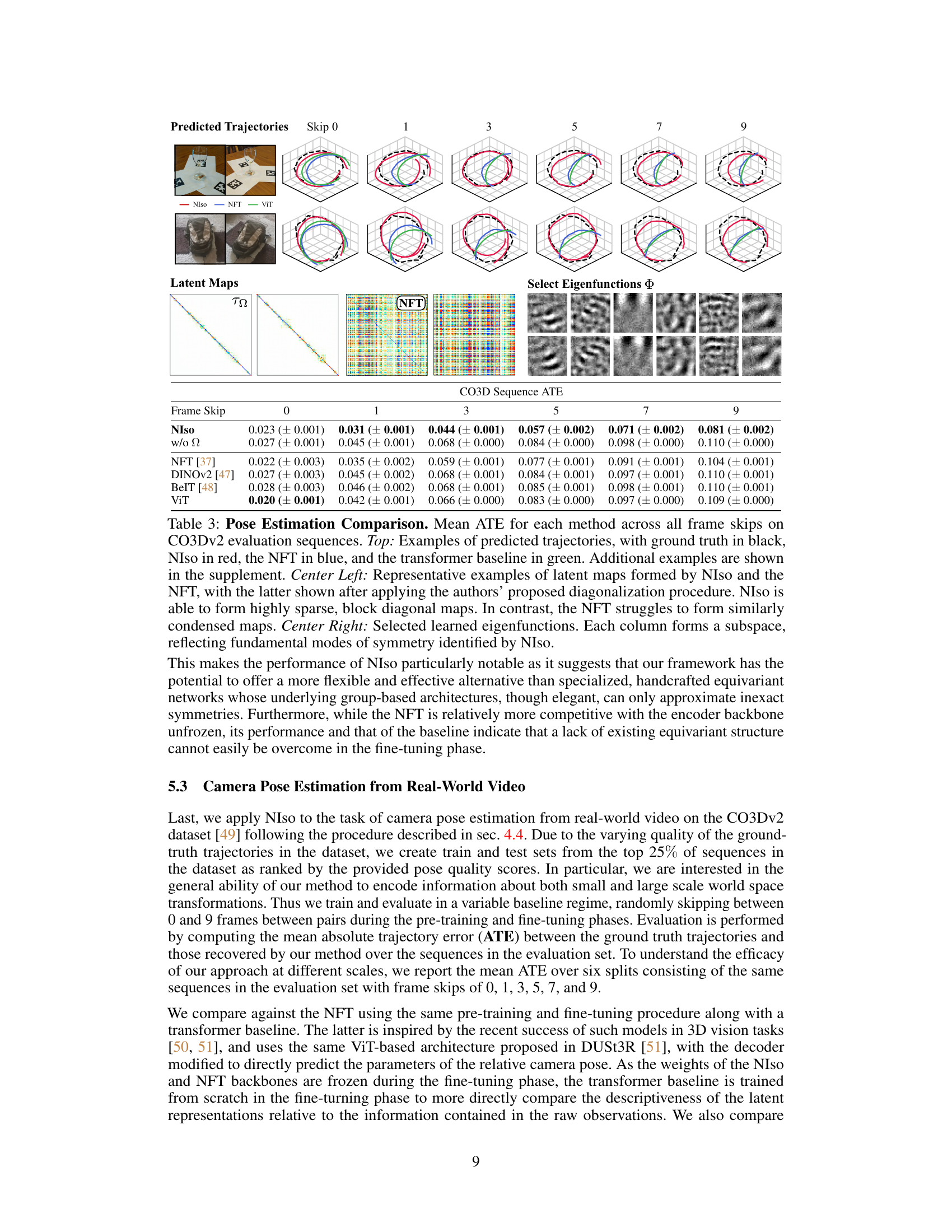
The figure illustrates the core idea of Neural Isometries. It shows how complex transformations in the observation space (e.g., images) are mapped to a latent space where the relationships between transformed encodings become tractable, represented as isometries. The input is transformed by an unknown transformation ‘T’, which results in a transformed output Tψ. Both the original and transformed outputs are encoded, using Encoder E, into latent representations. The relationship between these latent representations in the latent space is an Isometry, a transformation preserving distances and angles. This isometry makes it significantly easier for subsequent equivariant neural networks to handle these latent representations. The figure highlights the key advantage of Neural Isometries: transforming complex observation space transformations into simpler, tractable isometries in a latent space.

This table presents the classification accuracy results on the homography-perturbed MNIST dataset. It compares the performance of Neural Isometries (NIso) under various training conditions (with triplets, without equivariance loss, without multiplicity loss) against a Neural Fourier Transform (NFT) baseline, an autoencoder with data augmentation, and two state-of-the-art hand-crafted equivariant networks (homConv and LieDecomp). The results demonstrate the effectiveness of NIso’s approach and highlight the importance of its key components, specifically the isometric regularization.

In-depth insights
#

Isometric Latent Space
#

The concept of an “Isometric Latent Space” in machine learning is intriguing. It suggests a way to represent data in a lower-dimensional space where the geometric relationships between data points are preserved. This is crucial for tasks involving transformations, such as rotations or translations. Isometry ensures that distances and angles between points remain consistent across the transformation in both the original and latent space. This property is especially beneficial when dealing with complex, nonlinear transformations, where traditional methods might struggle. By mapping data into an isometric latent space, we could potentially make the learning process more efficient and robust. The choice of an appropriate distance metric in the latent space is vital for successful isometric embedding. The ability to learn isometric maps automatically, rather than relying on predefined ones, would greatly improve the applicability of this approach to various real-world scenarios and geometric data types. Moreover, the capacity to extract and use information about these maps for inferencing tasks, such as pose estimation, is a significant advantage. This approach to handling transformations in a latent space represents a noteworthy advancement with the potential to simplify and enhance various machine learning applications that struggle with geometric data.

Equivariant Autoencoders
#

Equivariant autoencoders represent a powerful paradigm shift in machine learning, especially in domains dealing with complex geometric transformations. They elegantly combine the data compression capabilities of autoencoders with the symmetry-preserving properties of equivariant models. The core idea is to learn a latent space where the encoding of transformed data is itself a transformed version of the original encoding, preserving the underlying geometric relationships. This approach is crucial for handling data with inherent symmetries, such as images under rotations or translations, or 3D shapes under rigid transformations. By ensuring equivariance, these models avoid the need for computationally expensive explicit handling of such transformations during both training and inference. This leads to significant gains in efficiency and often improved generalization. Furthermore, the disentangled latent space often allows for easier manipulation and analysis of the underlying data features. However, designing effective equivariant autoencoders presents several challenges, including the careful selection of appropriate group representations for the transformation, the architectural design for maintaining equivariance throughout the network, and ensuring the reconstruction quality is not compromised by the additional constraints of equivariance. Research in this area focuses on developing more flexible and efficient architectures, as well as exploring new applications to areas beyond the typical image and point cloud processing scenarios. The potential for these models to improve our understanding and application of data with rich geometric structures is enormous, making them a significant avenue for future research.

Latent Pose Regression
#

Latent pose regression, as a concept, offers a powerful approach to estimating poses within a learned latent space. Instead of directly regressing poses from raw sensory data (e.g., images), this method first maps the data into a latent representation where transformations have a simpler, more tractable form. This reduces the dimensionality and complexity of the problem, making pose estimation more efficient and robust. A key benefit is that the latent space can capture underlying geometric information which is often obscured in raw sensor data. Furthermore, this latent space can be learned in an unsupervised way, requiring only unlabeled data, which is often much easier to obtain than labeled data needed for supervised methods. The success of latent pose regression depends heavily on the effectiveness of the encoder network responsible for mapping the raw data to the latent space. The encoder must efficiently capture relevant geometric information while discarding irrelevant details. Finally, the choice of regression model for the latent space plays a significant role. The model’s ability to accurately capture the non-linear relationship between latent representations and poses is crucial. Despite its potential, challenges remain. The quality of pose estimations is intrinsically linked to the quality of the latent space and the expressiveness of the regression model, making careful design choices crucial for optimal performance.

Symmetry Discovery
#

Symmetry discovery in machine learning focuses on automatically identifying and exploiting inherent symmetries within data. This is crucial because explicitly encoding symmetries can lead to more efficient and robust models, particularly when dealing with complex transformations like those found in images or 3D shapes. Neural Isometries, for example, tackles symmetry learning by mapping observation spaces to a latent space where geometric relationships manifest as isometries (distance-preserving transformations). This approach avoids hand-crafting architectures tailored to specific known symmetries, allowing it to handle unknown or complex transformations. However, a key challenge remains in ensuring that the learned symmetries accurately reflect the underlying data structure, while also making the method computationally efficient and robust to noise or incomplete data. The discovery process itself needs further development, particularly in understanding how to best regularize the latent space, to learn meaningful symmetries, and to handle the computational complexity that can arise with high-dimensional data. Further research should focus on addressing these limitations to unlock the full potential of automated symmetry discovery in a wider range of applications.

Geometric Deep Learning
#

Geometric deep learning (GDL) focuses on designing neural networks that are inherently equivariant or invariant to transformations of the input data. This is particularly useful when dealing with data that has underlying geometric structures, such as images, point clouds, graphs, or meshes. Traditional deep learning approaches often struggle with such data because they lack the ability to explicitly encode geometric properties. GDL addresses this limitation by leveraging tools from group theory and differential geometry, allowing networks to learn representations that are robust to rotations, translations, and other transformations. This often involves using group representations or constructing architectures that naturally commute with the relevant geometric transformations. A key advantage of GDL is its ability to learn more efficient and generalizable representations, especially when dealing with limited training data. This is because the inherent geometric structure reduces the dimensionality of the problem. However, GDL techniques can be complex to design and implement, and are often limited to specific types of geometric structures and transformations. The field continues to advance by exploring new architectures, improving existing methods, and extending its applicability to a broader range of domains.

More visual insights
#

More on figures

This figure illustrates the Neural Isometries (NIso) framework. It shows how NIso learns a latent space where transformations in the input space (e.g., images) are represented as isometries (distance-preserving transformations) in the latent space. The process involves encoding input observations into latent functions, projecting them into an eigenbasis defined by a learned operator, estimating an isometric functional map between them, and then reconstructing transformed observations. Losses are used to enforce isometry equivariance in the latent space, accurate reconstruction of transformed data, and distinct eigenvalues of the learned operator to encourage a sparse, block diagonal isometric functional map. An optional spectral dropout layer can improve the ordering of the eigenvalues.

This figure illustrates the Neural Isometries (NIso) framework. It shows how NIso learns a latent space where transformations in the observation space (e.g., images) become isometric transformations in the latent space. This is achieved by regularizing the functional maps between latent representations to commute with a learned operator. The figure details the process, from encoding observations to estimating isometric maps and applying losses to enforce equivariance and reconstruction.

This figure shows the results of applying Neural Isometries (NIso) to learn representations of the Laplacian operator on the torus and sphere. The left side displays input images (ψ and Tψ) on the torus and sphere, respectively, undergoing shifts and rotations. The center shows the learned isometry (τΩ) in the latent space which maps between the encodings of these input images. A key observation is that τΩ is nearly diagonal, with blocks preserving the subspaces spanned by the learned eigenfunctions (Φ). The right shows that NIso recovers operators structurally similar to the toric and spherical Laplacians, with the learned eigenfunctions demonstrating similar properties to toric and spherical harmonics.

This figure illustrates the core idea of Neural Isometries. It shows how complex transformations in the original observation space (e.g., images) are mapped to a latent space where the relationships between transformed observations become simplified and tractable. This simplification is achieved by making the transformations in the latent space isometric, meaning they preserve distances and angles. The image depicts the transformation of input images through an encoder, creating isometrically related representations in a latent space, which then can be used by a generic equivariant neural network.

This figure shows the results of applying Neural Isometries (NIso) to learn operators on the torus and sphere. The left side shows input images on the torus (top) and sphere (bottom), with their transformed versions underneath. NIso successfully regresses operators (center right) highly similar in structure to the Laplacian on each manifold, demonstrated by diagonal maps (center left) and eigenfunctions that closely resemble the toric and spherical harmonics. The rightmost column shows ground truth Laplacian operators for comparison. The inset highlights the block-diagonal structure of the learned maps.

This figure illustrates the Neural Isometries (NIso) framework. It shows how NIso learns a latent space where geometric transformations in the input space (e.g., images) are represented as isometries (distance-preserving transformations) in the latent space. The process involves encoding observations into latent functions, projecting them into an operator eigenbasis, estimating an isometric functional map between them, and using losses to ensure isometry equivariance, reconstruction accuracy, and distinct eigenvalues.

This figure visualizes the learned eigenfunctions (Φ) and mass matrices (M) from three different experiments: Homography MNIST, Conformal SHREC ‘11, and CO3D. The top row shows the eigenfunctions, sorted by eigenvalue, while the bottom row displays the mass matrices, with color representing deviation from the mean mass value at each grid location. The visualization helps illustrate how the learned representations capture geometric information specific to each task.

This figure demonstrates the ability of Neural Isometries to learn operators similar to the Laplacian on the torus and sphere. By inputting shifted images on the torus and rotated images on the sphere, the model regresses operators whose structure and eigenvalues closely match those of the toric and spherical Laplacians. The diagonal structure of the maps (τΩ) highlights the preservation of subspaces spanned by eigenfunctions with similar eigenvalues, mirroring the properties of spherical harmonics. The close match between the learned spherical τΩ and the ground truth Wigner-D matrices further validates the model’s accuracy.

This figure shows the results of applying Neural Isometries (NIso) to learn representations of the Laplacian operator on the torus and sphere. NIso is able to learn operators that closely resemble the ground truth Laplacian operators, demonstrating its ability to discover meaningful geometric structure in latent space. The diagonal structure of the learned isometries (τΩ) in the eigenbasis is highlighted, indicating the preservation of subspaces spanned by the eigenfunctions. The figure also illustrates the learned eigenfunctions for both the torus and sphere, showing a close resemblance to the expected toric and spherical harmonics. This figure demonstrates the effectiveness of NIso in discovering and representing complex geometric transformations in a tractable way.

This figure shows the results of applying Neural Isometries (NIso) to learn operators on the torus and sphere. The model successfully approximates the Laplacian operator on both manifolds, demonstrating that NIso can discover approximations of known operators. The diagonal structure of the maps (τΩ) highlights the preservation of subspaces spanned by the learned eigenfunctions which share eigenvalues similar to spherical and toric harmonics.

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

Isometric Latent Space#

Equivariant Autoencoders#

Latent Pose Regression#

Symmetry Discovery#

Geometric Deep Learning#

More visual insights#

Full paper#