Conformalized Time Series with Semantic Features

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on uncertainty quantification in time series, a critical area in various fields. It offers a novel approach that significantly improves prediction efficiency and accuracy, thus advancing the state-of-the-art. The proposed method’s model-agnostic nature and theoretical guarantees make it widely applicable, and its focus on latent space learning opens new avenues for research in this domain. The adaptive weighting mechanism is also valuable, showcasing a flexible approach to handling complex temporal data.

Visual Insights

#

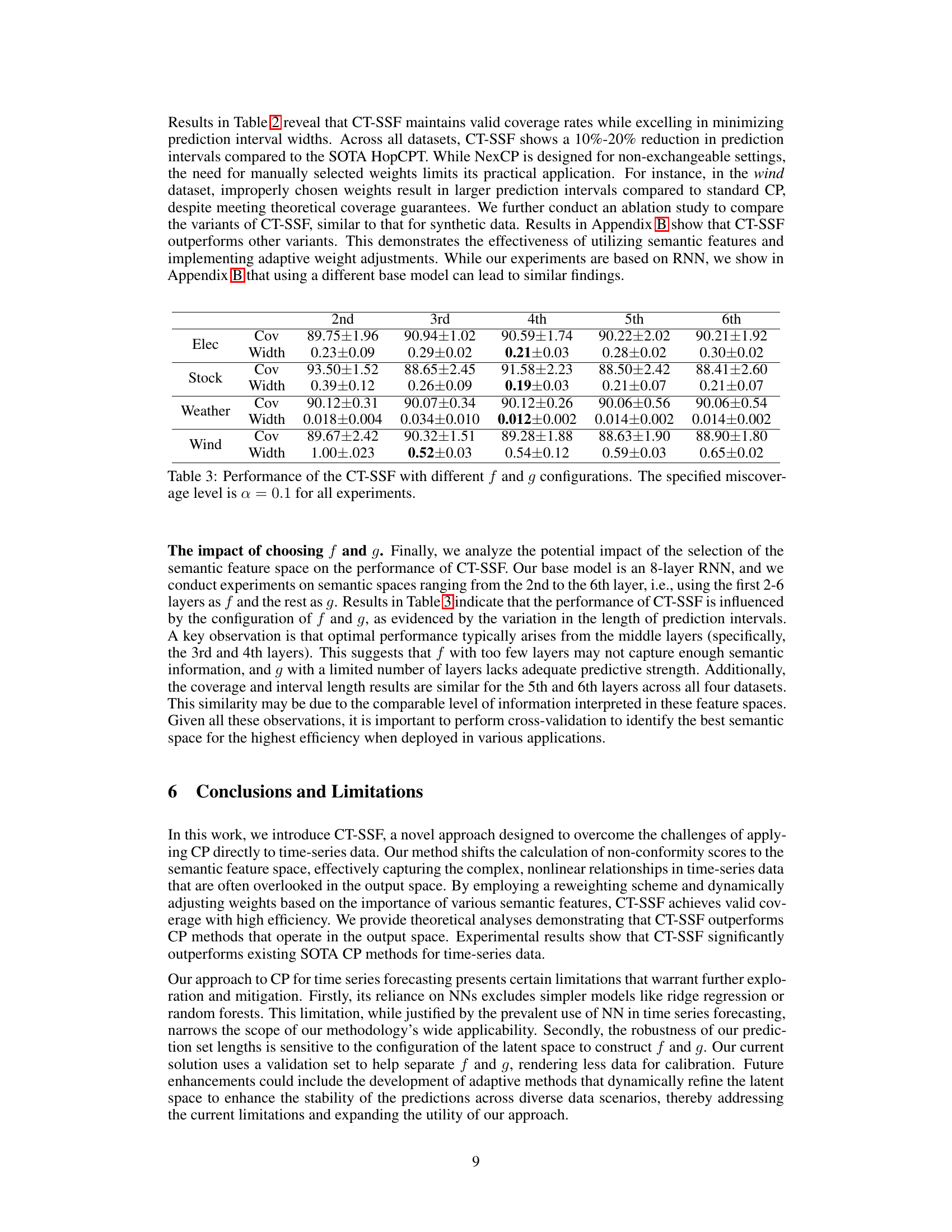
This figure compares the performance of CT-SSF against three variants: CT-MS (manually selected weights in the semantic space), CT-LO (learned weights in the output space), and CT-MO (manually selected weights in the output space). The comparison is done across different miscoverage rates (0.05 to 0.3). The blue bars represent the average prediction set width (efficiency), while the gray bars show the empirical coverage rate (reliability). The blue dashed line indicates the target coverage rate (1-α). The figure visually demonstrates that CT-SSF is more efficient (smaller width) while maintaining the desired coverage.

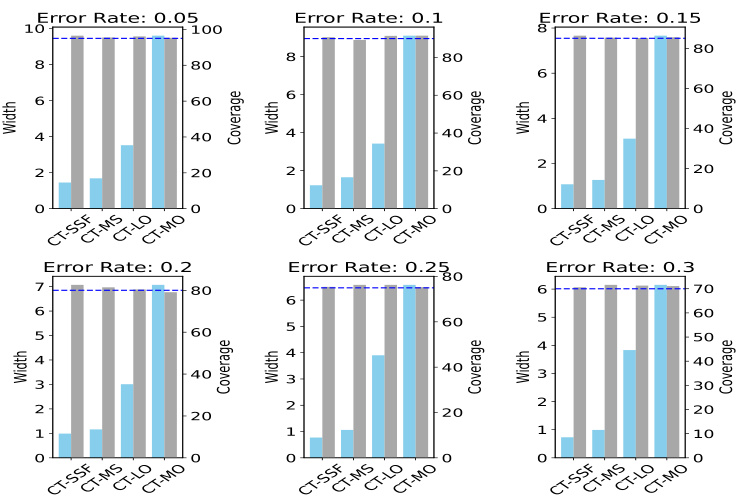
This table presents the performance of various conformal prediction (CP) algorithms on a simulated dataset. The algorithms compared include standard CP, FeatureCP (FCP), NexCP, HopCPT, and the proposed CT-SSF. The table shows the empirical coverage and average prediction set width for each algorithm across three different miscoverage error levels (0.05, 0.1, and 0.15). The results demonstrate CT-SSF’s improved prediction efficiency while maintaining valid coverage compared to other algorithms.

In-depth insights

#

Semantic CP

#

Semantic CP, a conceptual extension of conformal prediction (CP), aims to improve uncertainty quantification by incorporating semantic information. This approach acknowledges that raw data points may not fully capture the underlying meaning or relationships within the data. Instead of relying solely on numerical features, Semantic CP leverages semantic representations learned from models like deep neural networks to create a richer understanding of the data. This approach is crucial for handling complex data types, such as text, images, or time-series, where numerical features may not suffice. By incorporating semantic information, Semantic CP can potentially achieve tighter prediction intervals, leading to more accurate and efficient uncertainty quantification. However, challenges remain, such as how to effectively define and measure semantic similarity, which can vary widely depending on the data and the task. It also remains to be seen how well this method scales to massive datasets, and the computational cost of learning such rich representations should be carefully evaluated. Despite these challenges, Semantic CP represents a promising avenue for improving uncertainty quantification in various applications by moving beyond simplistic numerical representations to incorporate more nuanced semantic data.

Adaptive Weights

#

The concept of ‘adaptive weights’ in the context of conformalized time series prediction is crucial for handling non-exchangeability. Dynamically adjusting weights based on the relevance of data points to the current prediction is key. This addresses the limitations of static weighting schemes which struggle with distribution drift over time. By assigning higher weights to data more relevant to the present prediction and reducing the weight of data from the distant past, models can better capture the temporal dynamics in the data, reducing overconservatism and improving prediction efficiency. The effectiveness of adaptive weighting hinges on how effectively it prioritizes relevant information and its capability to generalize across various datasets. The successful implementation relies heavily on the choice of features used to determine weight adjustment, emphasizing the importance of utilizing semantically rich information as opposed to raw data. Successfully incorporating adaptive weights necessitates finding an optimal balance between responsiveness to recent data and retaining enough historical context to maintain statistical validity.

Latent Space CP

#

The concept of ‘Latent Space CP’, or Conformal Prediction applied within a latent feature space, presents a powerful advancement in uncertainty quantification, particularly for complex data like time series. By operating in the latent space instead of the output space, this approach leverages the richer, more informative representations learned by deep neural networks. This allows the model to capture nuanced relationships and temporal dependencies that might be invisible in the raw data, ultimately leading to more accurate and efficient prediction intervals. A key advantage is the potential for dynamic weight adaptation, which allows the model to prioritize relevant features in the latent space, dynamically adjusting to evolving data patterns and improving both coverage and efficiency. Theoretically, this approach is shown to outperform methods confined to the output space, offering tighter prediction intervals while maintaining valid coverage guarantees. However, careful consideration must be given to the choice of feature mapping function and the proper calibration to ensure the validity and reliability of the method. The computational cost and potential complexity of the latent space representation should also be considered.

Theoretical Guarantees

#

The Theoretical Guarantees section of a research paper would rigorously justify the proposed method’s claims. This involves proving formal statements about the method’s performance, such as coverage guarantees and efficiency bounds. For instance, a conformal prediction method might guarantee that its prediction intervals contain the true value with a specified probability (coverage). The proof would likely use statistical tools, possibly relying on assumptions about the data generating process or the model used. Formal proofs of coverage and efficiency would be crucial for establishing trust and reliability, allowing the method to be used confidently in high-stakes applications. The theoretical analysis should also explore how the method’s performance scales with dataset size and model complexity. This understanding is vital for determining the method’s suitability to real-world problems with potentially massive datasets. Ultimately, the strength of the theoretical guarantees directly impacts the practical value and trustworthiness of the research. A comprehensive theoretical framework builds confidence in the reliability and predictive power of the proposed approach.

Real-World Results

#

A dedicated ‘Real-World Results’ section would be crucial to demonstrate the practical applicability of the proposed CT-SSF method. It should present results on several diverse, real-world datasets, comparing CT-SSF’s performance against existing state-of-the-art (SOTA) conformal prediction methods for time series. Key metrics should include coverage (the percentage of true values falling within the prediction intervals), interval width (reflecting prediction precision), and computational efficiency. A thorough analysis should explore how CT-SSF adapts to various data characteristics and distribution shifts often found in real-world data. Visualizations, like box plots or line graphs showing interval widths across different datasets or methods, could aid intuitive understanding. A detailed discussion about the relative strengths and weaknesses of CT-SSF in different scenarios, and comparisons with other methods’ performance under those circumstances would also be insightful. Significant findings should be highlighted and their practical implications emphasized. The section should also discuss any limitations encountered while applying the method to real-world data, and how those limitations might be addressed in future work.

More visual insights

#

More on tables

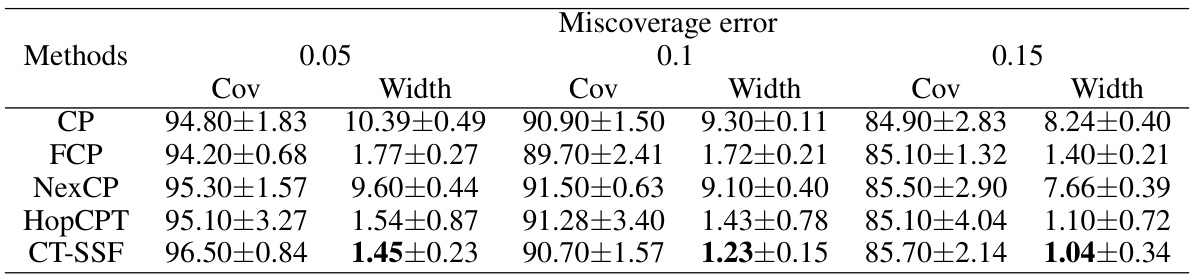
This table presents the performance of several conformal prediction (CP) methods on four real-world datasets (Electricity, Stock, Weather, and Wind). The performance is evaluated using two metrics: Empirical Coverage Rate (Cov) and Average Prediction Set Size (Width). The miscoverage level (α) is fixed at 0.1 for all experiments, but results for other α levels are available in Appendix B. The table allows comparison of CT-SSF against other CP methods like HopCPT, NexCP, FCP, and standard CP.

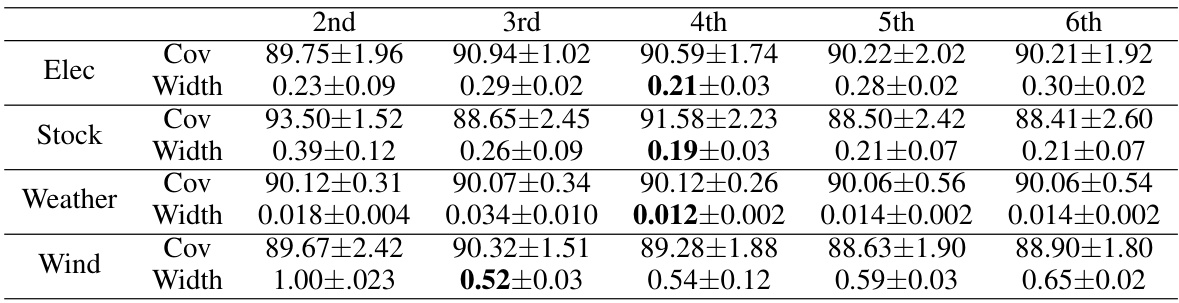
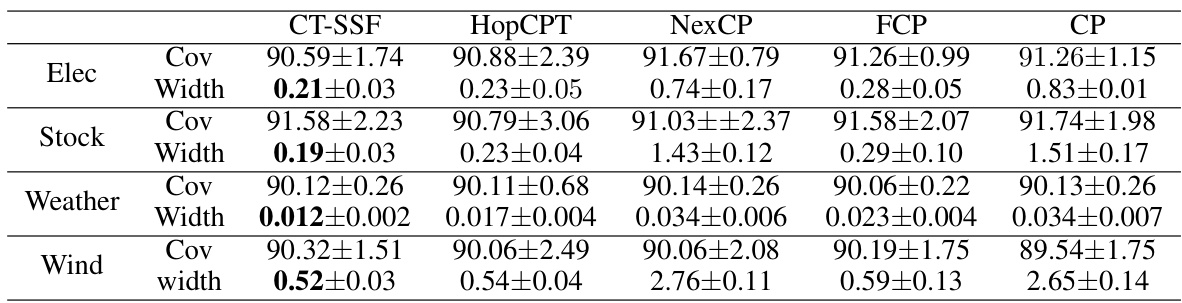
This table presents the results of experiments conducted to evaluate the impact of different choices for the feature extraction function (f) and prediction head (g) in the CT-SSF model. The table shows the empirical coverage and average width of the prediction intervals for various configurations (2nd to 6th layers used for f), with a miscoverage level α set to 0.1 across different datasets (Electricity, Stock, Weather, and Wind). The results demonstrate how the choice of f and g affects the performance of the model in terms of both coverage and prediction efficiency.

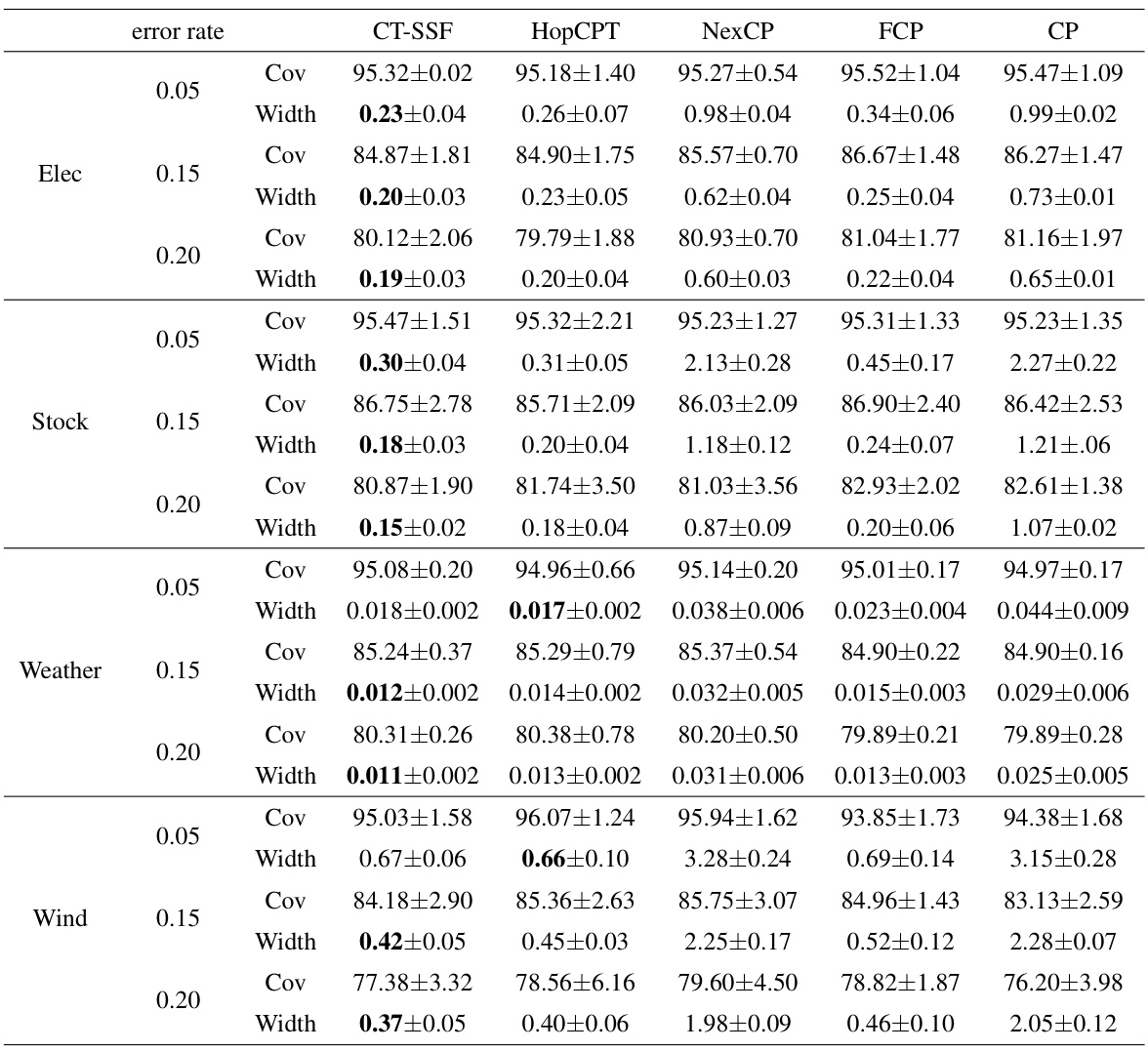
This table presents the performance of several conformal prediction (CP) algorithms on a synthetic time series dataset. The algorithms include standard CP, FCP, NexCP, HopCPT, and the proposed CT-SSF. Performance is evaluated across three different miscoverage error levels (0.05, 0.1, 0.15). The table shows the coverage and width (average prediction set size) for each algorithm and error rate, allowing for a comparison of efficiency and accuracy.

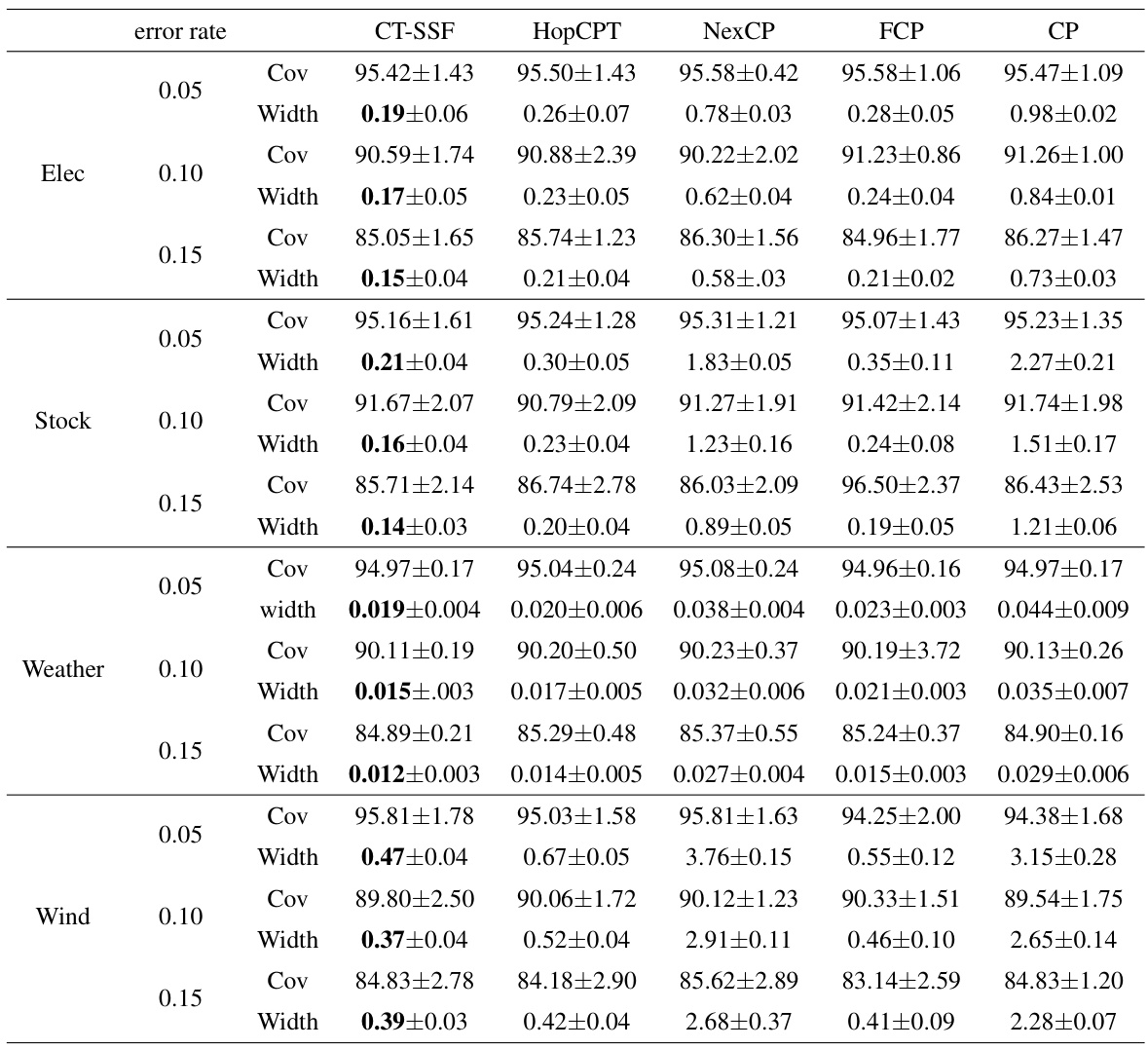
This table presents the performance of various conformal prediction (CP) algorithms on a simulated time series dataset. The algorithms evaluated include standard CP, FCP, NexCP, HopCPT, and the proposed CT-SSF. Performance is measured across three different miscoverage error levels (0.05, 0.1, and 0.15) using two metrics: coverage and width (average prediction set size). The results demonstrate CT-SSF’s superiority in terms of efficiency (smaller width) while maintaining a valid coverage guarantee.

Full paper

#