↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in imitation learning and causal inference. It addresses the critical issue of unobserved confounding, a common problem hindering the effectiveness of imitation learning algorithms. By introducing novel algorithms that leverage partial identification, the research provides robust solutions for learning effective policies even with incomplete knowledge of the system dynamics. This opens up new avenues for research in robust imitation learning, which is highly relevant in various domains involving sequential decision-making, such as robotics, autonomous driving, and healthcare.
Visual Insights#
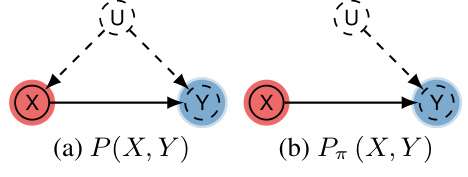
This figure illustrates a multi-armed bandit model with a binary action X ∈ {0, 1}, a binary reward Y, and a latent covariate U ∈ {0, 1} that affects both the action and reward. The reward function is defined as Y ← X ⊕ U, where ⊕ denotes the XOR operator. The figure shows two scenarios: (a) represents the joint probability distribution P(X, Y) and (b) the interventional distribution Pπ(X, Y), where π is a policy. This example demonstrates how unobserved confounding can affect imitation learning.

This table summarizes the main contributions of the paper. It shows the different scenarios considered based on whether the transition and reward functions are identifiable or not from the observed data. For each scenario, it indicates whether standard imitation learning methods apply, or if a novel causal imitation learning algorithm (CAIL) is proposed. The table also highlights the cases where imitation is theoretically impossible due to unobserved confounding.
In-depth insights#
Causal IL Challenges#
Causal imitation learning (IL), while promising, faces significant hurdles. Unobserved confounding, where latent variables influence both expert actions and outcomes, severely limits the ability of standard IL methods to guarantee performance matching the expert. This challenge stems from the inability to uniquely identify the underlying causal mechanisms, leading to a lack of robust policy learning. Partial identification offers a potential solution, allowing inference about causal effects despite this non-identifiability. However, even with partial identification, the problem remains complex. The interplay of identifiability of transition dynamics and reward functions significantly impacts the feasibility of effective imitation. Algorithms must be carefully designed to handle situations with either partially identifiable transitions or rewards, or both. Furthermore, the curse of dimensionality presents a practical barrier; high-dimensional state and action spaces make inference and optimization extremely difficult. Developing robust and computationally feasible algorithms that address these challenges remains a critical area of ongoing research.
Partial ID Approach#
The heading ‘Partial ID Approach’ suggests a methodology that addresses challenges in causal inference and imitation learning where complete knowledge of the system is unavailable. Partial identification techniques are employed to overcome the limitations of point-identification methods, which often require strong assumptions about the underlying causal structure. This approach allows for the analysis of systems with unobserved confounding and incomplete data by considering plausible ranges of values rather than precise point estimates. The implications are significant in enabling the development of more robust and practical algorithms that can function effectively even under conditions of uncertainty. It offers flexibility in handling complex scenarios where obtaining comprehensive information is impractical. The robustness of algorithms informed by this partial ID approach is a key benefit, leading to greater reliability and applicability in real-world applications where uncertainty is prevalent. By embracing the uncertainty inherent in these situations, the approach yields adaptable algorithms capable of handling incomplete information while still reaching meaningful conclusions.
Robust Imitation#
Robust imitation in machine learning focuses on creating agents capable of mimicking expert behavior even under challenging conditions. Noise, uncertainty, and distribution shifts are common issues that can compromise the effectiveness of standard imitation learning techniques. Robust methods address these issues by designing algorithms that are less sensitive to imperfections in the training data or variations in the environment. Techniques may include regularization, adversarial training, or incorporating domain knowledge to improve generalization. A key aspect of robust imitation is evaluating an agent’s ability to generalize to unseen scenarios and maintain performance. Theoretical guarantees that bound performance degradation under specific conditions are highly desirable. The ultimate goal is to develop learning systems that can reliably copy skills and strategies from demonstrations, offering practical applications across various fields.
GAIL Algorithm#
Generative Adversarial Imitation Learning (GAIL) is a powerful algorithm that enables agents to learn complex behaviors by imitating expert demonstrations. GAIL’s core strength lies in its ability to learn effectively without requiring explicit reward functions, a significant advantage in scenarios where defining rewards is difficult or impossible. The algorithm frames the learning process as a game between two neural networks: a policy network that tries to generate actions similar to the expert’s, and a discriminator network that tries to distinguish between the agent’s actions and those of the expert. This adversarial setup drives both networks to improve, leading to a policy that mimics expert behavior with impressive accuracy. A key advantage of GAIL over traditional imitation learning methods is its robustness to noisy or incomplete demonstrations. The adversarial training process allows it to focus on the most relevant aspects of the expert’s behavior and filter out irrelevant details. Despite its effectiveness, GAIL faces challenges like mode collapse, where the policy network might converge to a limited set of behaviors, and difficulty in handling high-dimensional state spaces. However, its capacity for learning complex behaviors in settings with limited information makes it an important algorithm in robotics, autonomous driving, and other fields.
Future Directions#
Future research could explore mitigating the impact of confounding bias in more complex scenarios, such as those involving continuous state and action spaces or partially observable environments. Investigating alternative causal identification methods beyond partial identification to enhance policy learning robustness would be valuable. The development of more efficient algorithms for solving the optimization problems presented in the paper, especially for high-dimensional settings, is crucial. Exploring the integration of causal imitation learning with other reinforcement learning techniques, such as reward shaping or curriculum learning, could yield significant improvements in sample efficiency and performance. Finally, applying these methods to real-world domains with rich datasets and diverse challenges—such as robotics, autonomous driving, and healthcare—would further validate their effectiveness and identify new areas for advancement. Addressing the ethical implications of using causal imitation learning, especially in contexts where unobserved confounders might perpetuate existing biases, is also a vital research avenue.
More visual insights#
More on figures
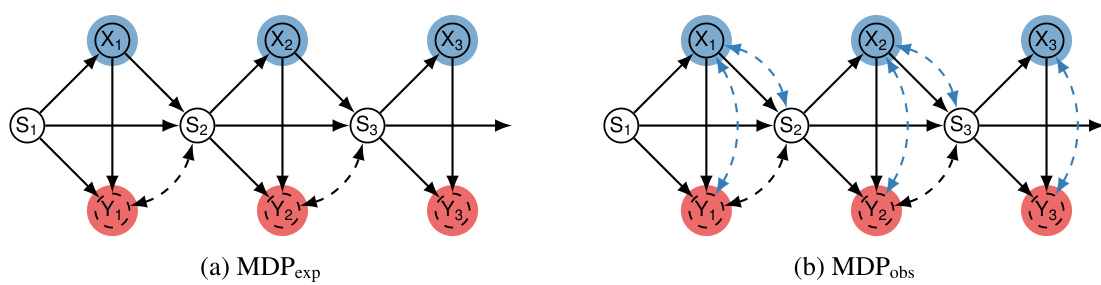
This figure shows two causal diagrams representing Markov Decision Processes (MDPs). The left diagram (a) shows the MDP from the imitator’s perspective, illustrating how the imitator interacts with the environment using actions (Xt) based on observed states (St) to receive rewards (Yt). The right diagram (b) represents the observational data available to the imitator, demonstrating how the expert’s actions and rewards are influenced by unobserved confounders (Ut) that are not visible to the imitator. This highlights the challenge of imitation learning when unobserved confounding is present.

This figure displays two causal diagrams illustrating Markov Decision Processes (MDPs). Diagram (a) shows the MDP from the imitator’s perspective, while diagram (b) illustrates the MDP generating the expert’s demonstration data. The key difference lies in the presence of an unobserved confounder U in diagram (b), affecting both the expert’s actions (Xt) and rewards (Yt). This unobserved confounder is crucial in highlighting the challenges posed by unobserved confounding bias in imitation learning. The diagrams use shaded blue for actions (Xt) and shaded red for latent rewards (Yt).

This figure presents the results of experiments comparing three imitation learning algorithms (CAIL, GAIL, and BC) against an expert in the MDPobs scenario. Panel (a) shows a histogram of the performance gap (imitator’s performance minus expert’s performance) for many runs of the MDPobs experiment, revealing a significant portion of runs where the imitator underperformed the expert. Panel (b) presents learning curves that illustrate the average return of each algorithm across epochs, demonstrating the convergence of the algorithms. Panel (c) displays the final average return for each method, indicating the relative performance of CAIL, GAIL, and BC compared to the expert.
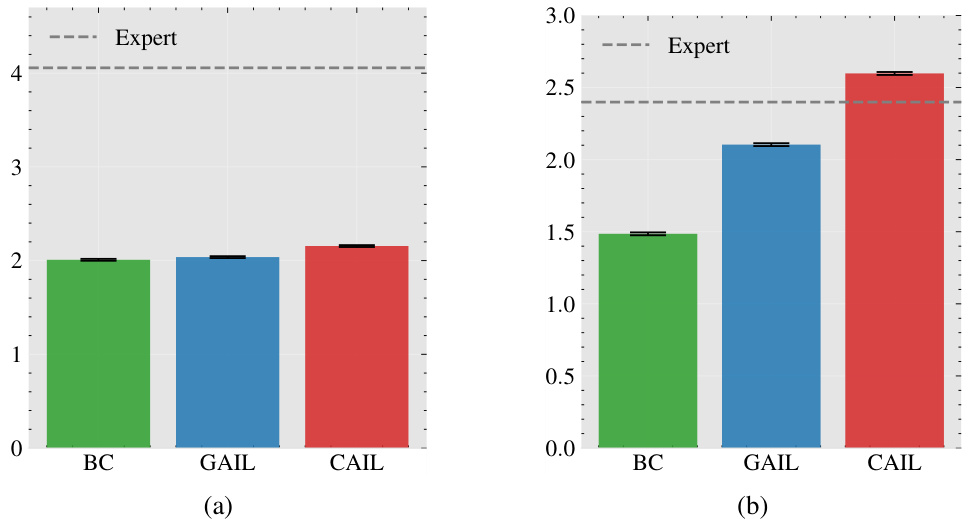
This figure presents simulation results comparing the performance of three imitation learning algorithms (CAIL, GAIL, and BC) against an expert. Subfigure (a) shows a histogram of the performance gap between each algorithm and the expert for a specific experiment (MDPobs). Subfigure (b) displays the learning curves of the three algorithms showing their performance over epochs. Subfigure (c) shows a bar chart of the final average return for each algorithm.
Full paper#



















