Immiscible Diffusion: Accelerating Diffusion Training with Noise Assignment

kK23oMGe9g

Yiheng Li et el.

↗ arXiv ↗ Hugging Face ↗ Hugging Face ↗ Chat

TL;DR
#

Diffusion models are powerful generative AI tools, but their training is notoriously slow due to inefficient noise-data mapping. Current methods diffuse each image across the entire noise space, creating a jumbled mixture that hinders optimization. This paper identifies this “miscibility” problem as the root cause of slow training.

To address this, the authors propose Immiscible Diffusion, a method that assigns noise to images based on their proximity in a mini-batch, preventing the random mixture of noise and data. This is achieved with a single line of code, leveraging a quantized assignment strategy for efficiency. Experiments show significant training speed improvements (up to 3x faster) on various datasets and models (Consistency Models, DDIM, Stable Diffusion) across different training scenarios (unconditional, conditional, fine-tuning). The improved training efficiency translates to better image quality, as demonstrated by lower FID scores and visual comparisons.

Key Takeaways
#

Why does it matter?
#

This paper is important because it addresses a critical bottleneck in diffusion model training: slow convergence due to suboptimal noise-data mapping. By introducing a simple yet effective method, Immiscible Diffusion, it significantly accelerates training speed (up to 3x faster) while improving image quality. This opens up new avenues for researchers to develop more efficient and high-quality generative AI models, potentially enabling faster research iterations and broader accessibility to this technology.

Visual Insights
#

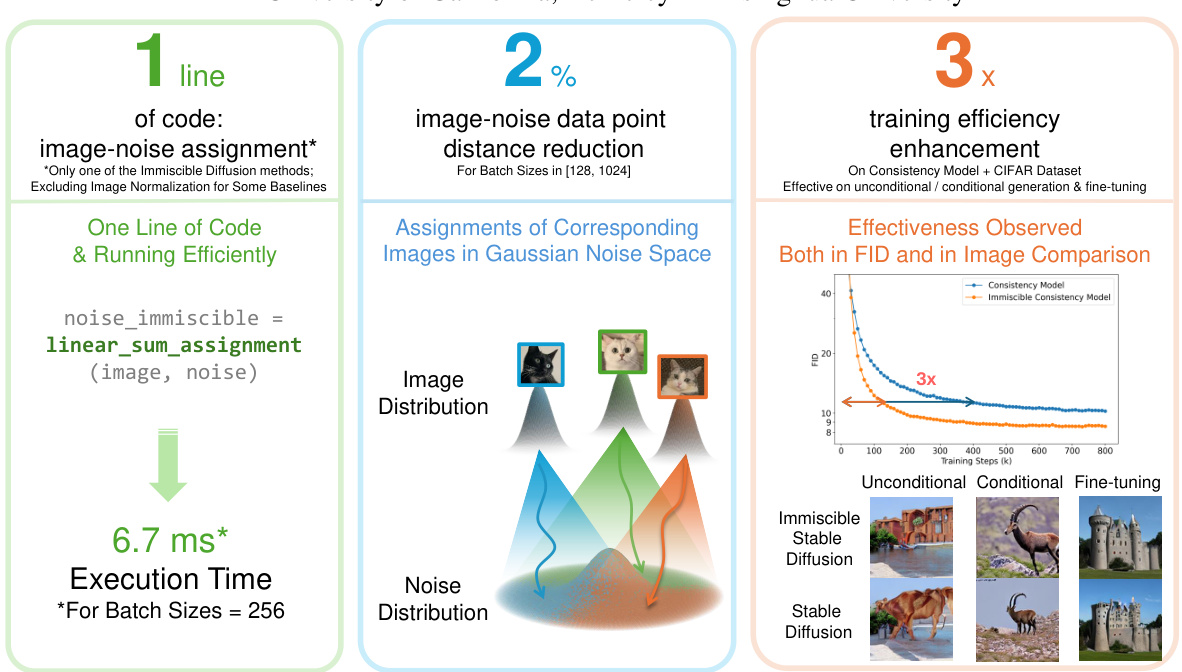
🔼 This figure summarizes the key results of the Immiscible Diffusion method. It shows that with a single line of code, the method achieves immiscibility (meaning the noise assigned to each image is distinct, not a random mixture), resulting in a minimal distance reduction (only 2%) yet a significant increase in training efficiency (up to 3x faster than the baseline on CIFAR-10 dataset). The improved efficiency translates to better image quality in Stable Diffusion on ImageNet, improving both unconditional and conditional generation and both training from scratch and fine-tuning tasks.
read the caption
Figure 1: Immiscible Diffusion can use a single line of code to efficiently achieve immiscibility by re-assigning a batch of noise to images. This process results in only a 2% reduction in distance post-assignment, leading to up to 3x increased training efficiency on top of the Consistency Model for CIFAR Dataset. Additionally, Immiscible Diffusion significantly enhances the image quality of Stable Diffusion for both unconditional and conditional generation tasks, and for both training from scratch and fine-tuning training tasks, on ImageNet Dataset within the same number of training steps.

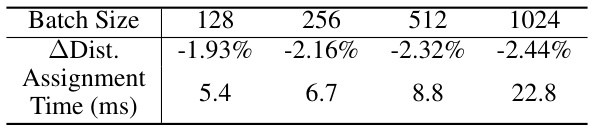
🔼 This table shows the percentage reduction in the L2 distance between image and noise data points after applying the linear assignment method, for different batch sizes. It also shows the time taken for the assignment process in milliseconds (ms). The negative percentage indicates a reduction in distance, suggesting the effectiveness of the assignment in bringing images and their corresponding noise closer together.
read the caption
Table 2: Image-noise data-point L2 distance reduction after the assignment for minimizing it and the time cost for the assignment.

In-depth insights
#

Immiscible Diffusion
#

The concept of “Immiscible Diffusion” presents a novel approach to enhance diffusion model training. By drawing an analogy from the immiscibility phenomenon in physics, where different substances resist mixing, the authors propose a method to improve the suboptimal noise-data mapping inherent in traditional diffusion models. This is achieved by strategically assigning noise to data points, thereby reducing the complexity of the optimization process and leading to faster convergence and improved image quality. The core idea is to disentangle the noise space, preventing images from becoming an indiscriminate mixture during the diffusion process, thus facilitating a more efficient reverse diffusion and denoising phase. The simplicity of implementation, involving a single line of code, is a significant advantage. However, the method’s reliance on a quantized assignment strategy to mitigate computational complexity needs further exploration. While effective, further investigation into the trade-offs between computational cost and training efficiency is required. Ultimately, “Immiscible Diffusion” offers a promising avenue for accelerating diffusion model training and improving generated image fidelity, but its broader implications and limitations require additional scrutiny.

Noise Assignment
#

The concept of ‘Noise Assignment’ in the context of diffusion models is crucial for understanding how the model learns to denoise images effectively. The core idea is to strategically map noise vectors to input images, not randomly, in order to improve the optimization process during training. Suboptimal mappings can lead to slow convergence and inferior results. Instead, assigning noise based on proximity to the image in a latent space creates a more disentangled relationship between data and noise, preventing the model from encountering a jumbled mixture of all images during denoising. This strategic assignment enhances training efficiency by facilitating clearer denoising pathways, thus leading to faster convergence and improved image quality. The effectiveness relies on the careful balance between maintaining the overall Gaussian noise distribution while achieving this structured mapping. This controlled assignment reduces the complexity of the optimization problem, enabling the model to more efficiently learn the denoising function, resulting in faster and better training outcomes. The use of techniques like linear assignment further enhances efficiency while ensuring the maintenance of desirable noise properties.

Training Efficiency
#

The research paper analyzes training efficiency in diffusion models, highlighting the significant computational cost associated with traditional methods. Suboptimal noise-data mapping is identified as a primary bottleneck, causing slow convergence. The paper proposes Immiscible Diffusion, a novel technique that addresses this issue by strategically assigning noise to data points, reducing the complexity of the optimization problem. Experimental results demonstrate significant improvements in training efficiency across various datasets and models (Consistency Models, DDIM, Stable Diffusion), achieving up to 3x speedup in some cases. The efficiency gains are attributed to improved disentanglement of data and noise during the training process, thereby simplifying the optimization landscape. Immiscibility, inspired by a physical phenomenon, proves key in improving performance. Despite the efficiency improvements, the computational cost of the assignment process, while mitigated through quantization, is still a factor influencing overall efficiency. Future directions involve enhancing the assignment strategy and testing the approach on larger-scale datasets.

Empirical Results
#

The empirical results section of a research paper is critical for demonstrating the validity of the study’s claims. A strong empirical results section will clearly present the data, using appropriate visualizations like graphs and tables, and will provide a thorough statistical analysis to determine the significance of the findings. The results should be presented in a way that is easy to understand and interpret, even for readers who are not experts in the specific field. Any limitations of the data or methodology should also be addressed. A well-written empirical results section will not only support the paper’s main claims but will also provide valuable insights into the broader research area. Careful attention to detail in this section can significantly impact the overall impact of the paper. Furthermore, a strong empirical results section provides the groundwork for robust conclusions, fostering trust and understanding among readers about the study’s contribution.

Future Works
#

The paper’s ‘Future Works’ section could explore several promising avenues. Extending the Immiscible Diffusion method to larger datasets and higher-resolution images is crucial for real-world applicability. Investigating the optimal assignment strategy beyond simple linear assignment, perhaps incorporating more sophisticated methods like optimal transport, is another key direction. Analyzing the interaction between Immiscible Diffusion and other training optimization techniques could lead to synergistic improvements. Exploring the method’s performance in other diffusion model architectures and generative tasks beyond those tested would further solidify its value. A thorough investigation into the theoretical underpinnings of Immiscible Diffusion, potentially deriving a principled understanding of its relationship to noise-data disentanglement, could be insightful. Finally, applying the Immiscible Diffusion concept to other generative modeling paradigms or to tasks beyond image generation would highlight its broader potential.

More visual insights
#

More on figures

🔼 The figure illustrates the concept of immiscible diffusion in both physics and image generation. Panel (a) shows how miscible particles mix completely, while immiscible particles maintain distinct regions even after diffusion. Panel (b) translates this to image generation, showing how vanilla diffusion methods produce a complete mix of image and noise data, making optimization difficult. In contrast, the Immiscible Diffusion method maintains distinct mappings between image and noise regions, making optimization easier.
read the caption
Figure 2: Physics illustration of Immiscible Diffusion. (a) depict the miscible and Immiscible Diffusion phenomenon in physics, while (b) demonstrate the image-noise pair relation in vanilla (miscible) and Immiscible Diffusion method.

🔼 This figure compares the denoising process of vanilla DDIM and Immiscible DDIM. It shows that while both methods use similar sampled noise, Immiscible DDIM produces significantly better denoised images, particularly in the noisier layers. This is because traditional methods struggle to accurately predict noise in these layers, while Immiscible DDIM excels at this.
read the caption
Figure 3: Feature analysis of vanilla (miscible) and immiscible DDIM. Referring to [45], τ = S represents the layer denoising from the pure noise. We show that while the two sampled noises are similar, the denoised image of immiscible DDIM significantly outperforms that of the traditional one, generating an overall reasonable image. The reason behind this is traditional methods cannot successfully predict noises at noisy layers.

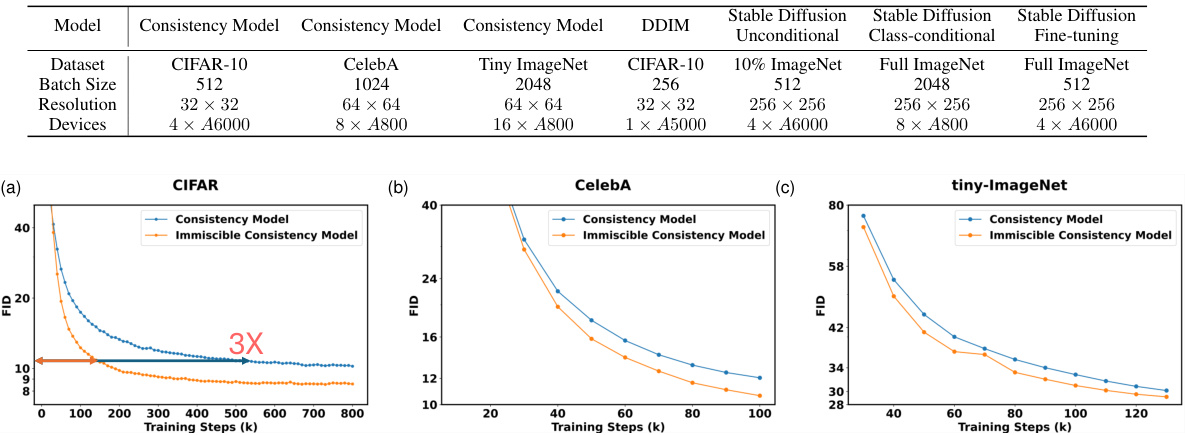
🔼 This figure compares the FID (Fréchet Inception Distance) scores of baseline and immiscible Consistency Models trained on three different datasets (CIFAR-10, CelebA, and Tiny-ImageNet) with varying training steps. The results show that the immiscible models achieve significantly lower FID scores with fewer training steps, demonstrating their higher training efficiency. The 3x improvement highlighted in the CIFAR-10 plot emphasizes the substantial speedup.
read the caption
Figure 4: Evaluation of baseline and immiscible Consistency Models on (a) CIFAR-10, (b) CelebA, and (c) tiny-ImageNet dataset. We illustrate the FID of two models with different training steps. Clearly, immiscible Consistency Models have much higher efficiency than the vanilla ones.

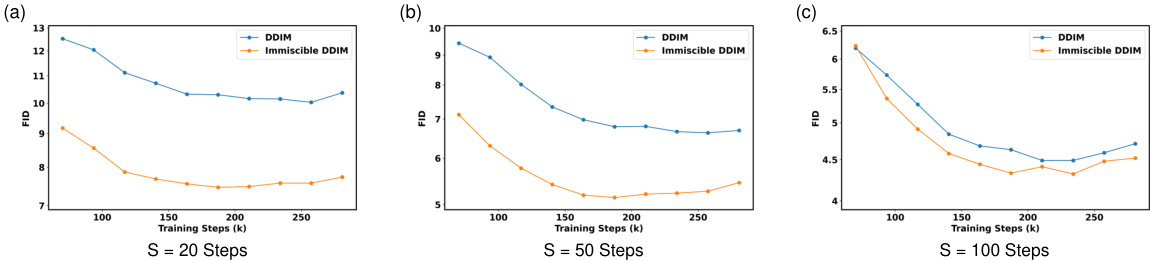
🔼 This figure shows the FID (Fréchet Inception Distance) scores for baseline DDIM and Immiscible DDIM models trained on the CIFAR-10 dataset. Three subplots are presented, each representing a different number of inference steps (S): 20, 50, and 100. The results demonstrate that Immiscible DDIM consistently achieves lower FID scores than the baseline DDIM across all three inference step settings, indicating improved image generation quality. The improvement is particularly pronounced when fewer inference steps are used (S=20).
read the caption
Figure 5: Evaluation of baseline and Immiscible DDIM on CIFAR-10 dataset with different inference steps S. We find that Immiscible DDIM outperforms the baseline more significantly when the number of inference steps S is smaller.

🔼 This figure shows the FID (Fréchet Inception Distance) scores for baseline and immiscible Consistency Models trained on three different datasets: CIFAR-10, CelebA, and tiny-ImageNet. The x-axis represents the number of training steps, and the y-axis represents the FID score. Lower FID scores indicate better image quality. The figure demonstrates that the immiscible Consistency Model converges to a lower FID score much faster than the baseline model for all three datasets, indicating significantly improved training efficiency. The plots visually represent the faster convergence of the immiscible model to a lower FID, signifying its superior training efficiency compared to the traditional model.
read the caption
Figure 4: Evaluation of baseline and immiscible Consistency Models on (a) CIFAR-10, (b) CelebA, and (c) tiny-ImageNet dataset. We illustrate the FID of two models with different training steps. Clearly, immiscible Consistency Models have much higher efficiency than the vanilla ones.

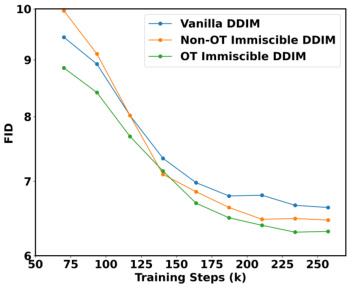
🔼 This figure shows the ablation study of Optimal Transport (OT) in the Immiscible Diffusion method. Three different FID curves are plotted: Vanilla DDIM, Non-OT Immiscible DDIM, and OT Immiscible DDIM. The FID values are plotted against the training steps. The results indicate that Immiscible Diffusion, rather than OT, is the primary factor contributing to performance improvement.
read the caption
Figure 7: Ablation of OT in Immiscible Diffusion. FIDs of OT and non-OT Immiscible Diffusion indicates that it is the Immiscible Diffusion rather than OT that dominate the performance enhancement.

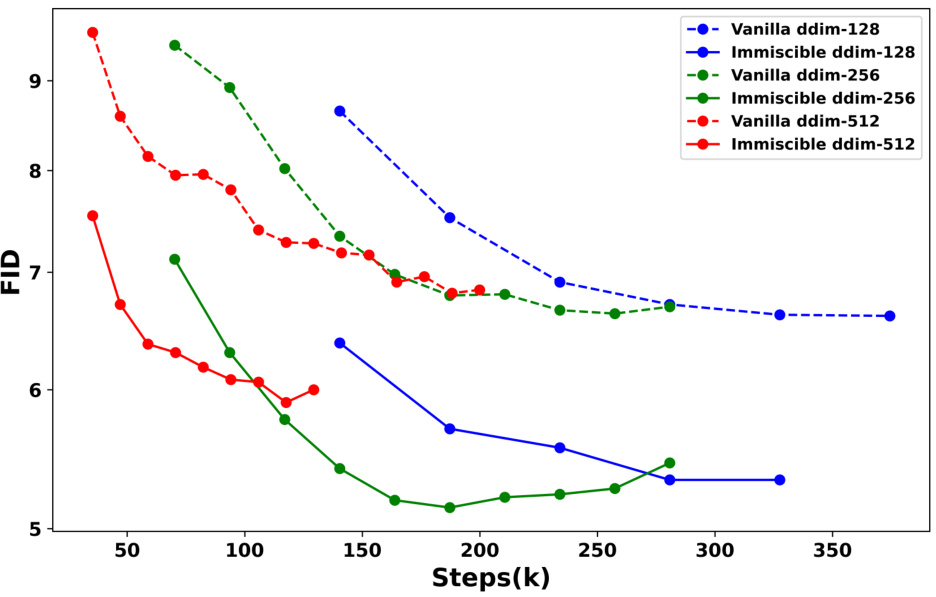
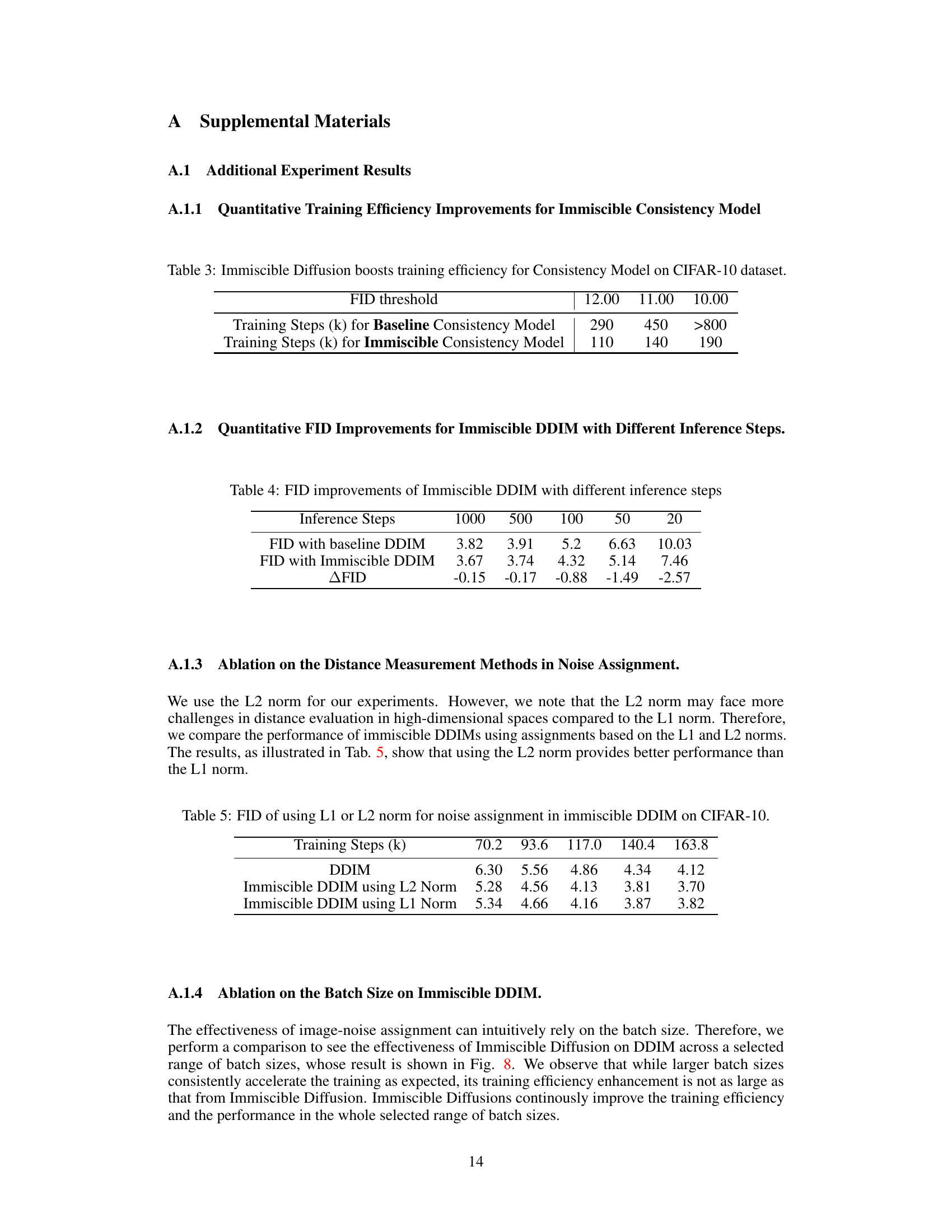
🔼 The figure shows the FID scores for both vanilla and immiscible DDIM models trained on CIFAR-10 dataset with different batch sizes (128, 256, 512). The x-axis represents the number of training steps (in thousands), and the y-axis represents the FID score. The plot demonstrates that Immiscible DDIM consistently outperforms vanilla DDIM across all batch sizes, achieving lower FID scores at various training steps. This suggests that the Immiscible Diffusion technique improves training efficiency regardless of the batch size used.
read the caption
Figure 8: Effectiveness of Immiscible DDIM in a selected range of batch sizes.

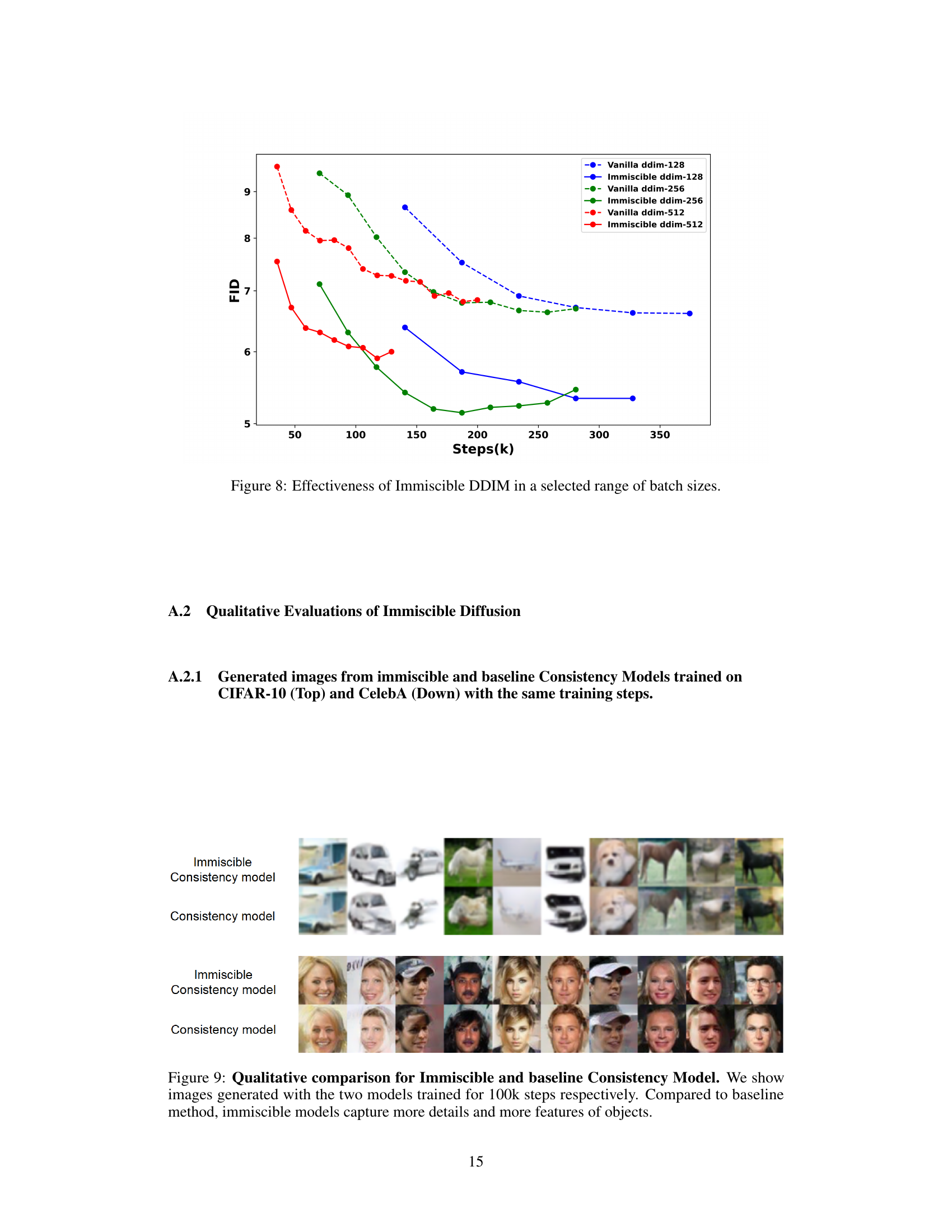
🔼 This figure shows a qualitative comparison of images generated by Immiscible and baseline Consistency Models. The models were trained for 100,000 steps each. The top row displays images generated from CIFAR-10, showing significantly clearer and more detailed images from the Immiscible model. The bottom row shows images generated from CelebA, again highlighting the superior detail and feature capture by the Immiscible model. This visual comparison directly supports the paper’s claims of improved image quality with Immiscible Diffusion.
read the caption
Figure 9: Qualitative comparison for Immiscible and baseline Consistency Model. We show images generated with the two models trained for 100k steps respectively. Compared to baseline method, immiscible models capture more details and more features of objects.

🔼 This figure summarizes the core idea and results of Immiscible Diffusion. It shows that with a simple one-line code change, the method achieves immiscibility in noise assignment, resulting in a 2% reduction in image-noise distance and a 3x speedup in training for CIFAR-10 dataset. The improved image quality of Stable Diffusion on ImageNet, across various generation tasks and training scenarios, is also highlighted.
read the caption
Figure 1: Immiscible Diffusion can use a single line of code to efficiently achieve immiscibility by re-assigning a batch of noise to images. This process results in only a 2% reduction in distance post-assignment, leading to up to 3x increased training efficiency on top of the Consistency Model for CIFAR Dataset. Additionally, Immiscible Diffusion significantly enhances the image quality of Stable Diffusion for both unconditional and conditional generation tasks, and for both training from scratch and fine-tuning training tasks, on ImageNet Dataset within the same number of training steps.

🔼 This figure demonstrates the effectiveness of Immiscible Diffusion. A single line of code reassigns noise to images, resulting in only a 2% reduction in image-noise distance but a 3x increase in training efficiency for the CIFAR dataset using the Consistency Model. Immiscible Diffusion also improves image quality for Stable Diffusion on ImageNet, regardless of whether the model is trained from scratch or fine-tuned.
read the caption
Figure 1: Immiscible Diffusion can use a single line of code to efficiently achieve immiscibility by re-assigning a batch of noise to images. This process results in only a 2% reduction in distance post-assignment, leading to up to 3x increased training efficiency on top of the Consistency Model for CIFAR Dataset. Additionally, Immiscible Diffusion significantly enhances the image quality of Stable Diffusion for both unconditional and conditional generation tasks, and for both training from scratch and fine-tuning training tasks, on ImageNet Dataset within the same number of training steps.

🔼 The figure shows a comparison of Immiscible Diffusion and other methods in terms of training efficiency and image quality. Immiscible Diffusion achieves a 3x speedup in training and improved image quality with only a single line of code change.
read the caption
Figure 1: Immiscible Diffusion can use a single line of code to efficiently achieve immiscibility by re-assigning a batch of noise to images. This process results in only a 2% reduction in distance post-assignment, leading to up to 3x increased training efficiency on top of the Consistency Model for CIFAR Dataset. Additionally, Immiscible Diffusion significantly enhances the image quality of Stable Diffusion for both unconditional and conditional generation tasks, and for both training from scratch and fine-tuning training tasks, on ImageNet Dataset within the same number of training steps.

🔼 This figure shows the effectiveness of Immiscible Diffusion. A single line of code reassigns noise to images, resulting in a 2% distance reduction and a 3x training efficiency increase for CIFAR-10. Image quality is also improved for Stable Diffusion on ImageNet.
read the caption
Figure 1: Immiscible Diffusion can use a single line of code to efficiently achieve immiscibility by re-assigning a batch of noise to images. This process results in only a 2% reduction in distance post-assignment, leading to up to 3x increased training efficiency on top of the Consistency Model for CIFAR Dataset. Additionally, Immiscible Diffusion significantly enhances the image quality of Stable Diffusion for both unconditional and conditional generation tasks, and for both training from scratch and fine-tuning training tasks, on ImageNet Dataset within the same number of training steps.

🔼 This figure shows a qualitative comparison of images generated by the immiscible and baseline Stable Diffusion models. Both models were trained unconditionally on 10% of the ImageNet dataset for 70,000 steps. The images demonstrate that the immiscible Stable Diffusion model produces images with more details and better overall quality than the baseline model.
read the caption
Figure 15: Generated images from immiscible and baseline stable diffusion models trained unconditionally on 10% ImageNet Dataset for 70k steps without cherry-picking

🔼 This figure shows a qualitative comparison of images generated by the immiscible and baseline Stable Diffusion models after 70k training steps on a subset of the ImageNet dataset. The immiscible model produces images with more coherent and realistic details compared to the baseline.
read the caption
Figure 14: Images generated by immiscible and baseline Stable Diffusion trained unconditionally on ImageNet for 70k steps. We see that the Immiscible Stable Diffusion presents more reasonable modal and catch more general features and details.

🔼 This figure summarizes the key findings of the Immiscible Diffusion method. It highlights that a simple one-line code change leads to a significant speedup in diffusion model training (up to 3x faster) and improved image quality, with minimal impact on the overall distance between image and noise data points. The effects are observed across different datasets (CIFAR and ImageNet) and training tasks (unconditional generation, conditional generation, and fine-tuning).
read the caption
Figure 1: Immiscible Diffusion can use a single line of code to efficiently achieve immiscibility by re-assigning a batch of noise to images. This process results in only a 2% reduction in distance post-assignment, leading to up to 3x increased training efficiency on top of the Consistency Model for CIFAR Dataset. Additionally, Immiscible Diffusion significantly enhances the image quality of Stable Diffusion for both unconditional and conditional generation tasks, and for both training from scratch and fine-tuning training tasks, on ImageNet Dataset within the same number of training steps.

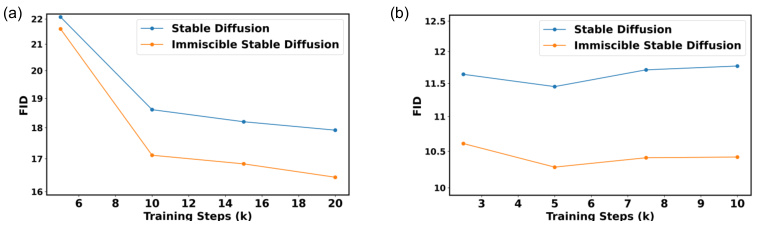
🔼 This figure shows the results of experiments comparing the baseline and immiscible class-conditional Stable Diffusion models on the ImageNet dataset. Two versions of the model are evaluated: one trained from scratch and one fine-tuned from Stable Diffusion v1.4. The Fréchet Inception Distance (FID) metric is used to evaluate the generated images, providing a quantitative measure of the quality of the generated samples. The results demonstrate the performance improvements achieved with the Immiscible Diffusion method across both training scenarios (from scratch and fine-tuning).
read the caption
Figure 6: Evaluation of baseline and immiscible class-conditional Stable Diffusion on ImageNet dataset, using 20 inference steps. (a) FID of two models trained from scratch (b) FID of two models fine-tuned on Stable Diffusion v1.4.

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

Immiscible Diffusion#

Noise Assignment#

Training Efficiency#

Empirical Results#

Future Works#

More visual insights#

Full paper#