↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Discrete diffusion models, while successful for tasks like text generation, suffer from slow sampling. Current acceleration techniques require additional training. This limits their application to large datasets and complex tasks.
This paper proposes Discrete Non-Markov Diffusion Models (DNDM) which solve this problem. DNDM introduces a training-free sampling algorithm by leveraging predetermined transition times. This significantly reduces the computational cost by decreasing the number of function evaluations. The superior performance of DNDM compared to other methods is demonstrated via experiments on natural language generation and machine translation. Furthermore, an infinite-step sampling approach is presented, providing new insights into discrete and continuous-time diffusion models.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in generative modeling, particularly those working with discrete data. It introduces a novel, training-free sampling algorithm that significantly speeds up discrete diffusion models. This advancement addresses a major bottleneck in the field and opens up new avenues for applying diffusion models to large-scale tasks that were previously computationally infeasible. The provided codebase ensures reproducibility, making the research highly impactful for the community.
Visual Insights#
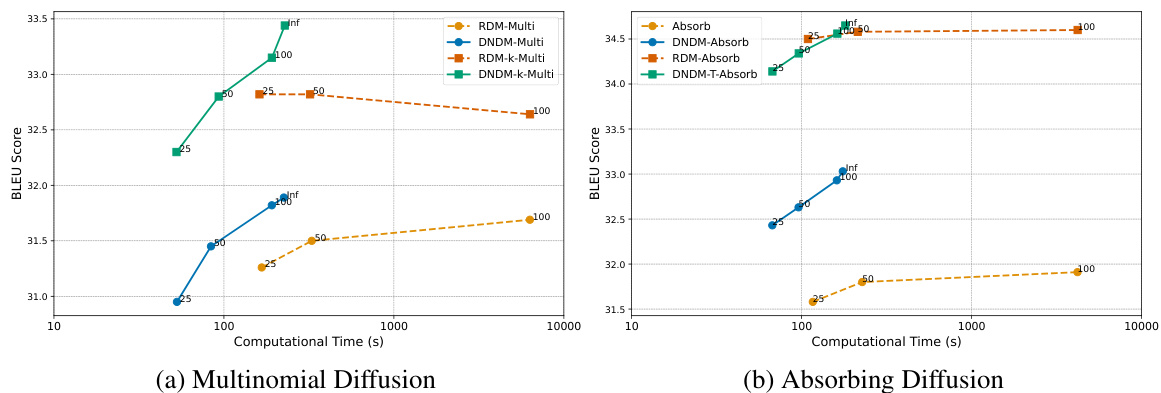
This figure compares the generation quality (BLEU score) against the computational time for different models on the IWSLT14 dataset. It shows the relationship between the BLEU score and computational time for various models including RDM-Multi, DNDM-Multi, RDM-k-Multi, and DNDM-k-Multi for both multinomial and absorbing diffusion. The steeper slope of a line indicates a larger improvement in BLEU score for a given increase in computational time, suggesting a better tradeoff between quality and speed. The figure highlights the superior efficiency of the DNDM models in achieving higher BLEU scores with lower computational cost compared to the baseline models.

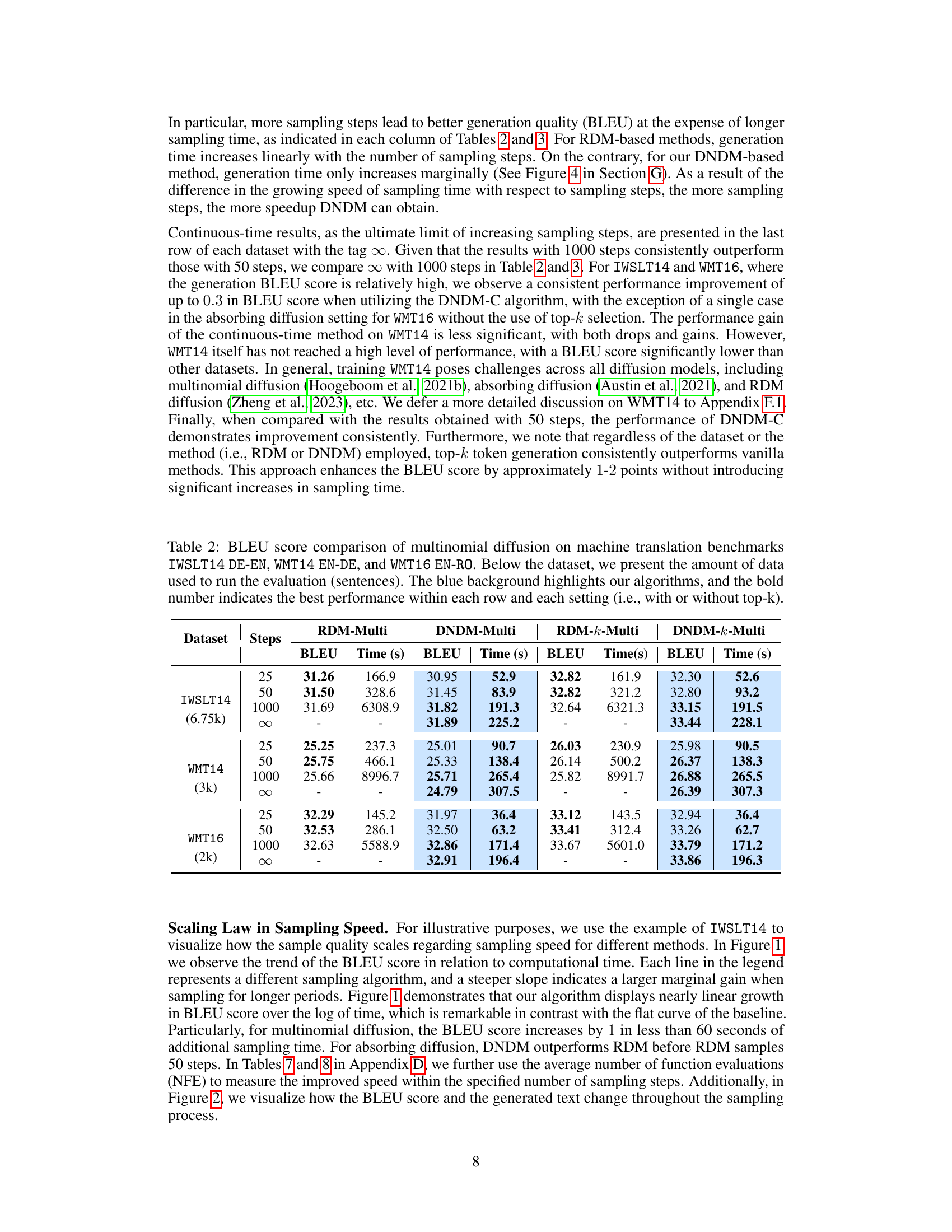
This table presents the BLEU scores and inference times for different models on three machine translation datasets (IWSLT14, WMT14, and WMT16). It compares the performance of the proposed DNDM-Multi and DNDM-k-Multi models against RDM-Multi and RDM-k-Multi baselines. The table shows results for different numbers of sampling steps (25, 50, 1000, and ∞), allowing comparison of speed and accuracy tradeoffs.
In-depth insights#
DNDM: Fast Sampling#
The proposed method, DNDM (Discrete Non-Markov Diffusion Model), tackles the challenge of slow sampling in discrete diffusion models. It introduces non-Markovian dynamics which cleverly leverages the inherent properties of discrete noise distributions. Instead of incrementally denoising through a fixed number of steps, DNDM strategically introduces a ’transition time’ variable, controlling when noise is actually replaced with a predicted token. This enables a training-free sampling algorithm that significantly reduces the number of function evaluations, leading to faster generation. The model’s effectiveness is demonstrated through empirical results on various text generation tasks, showcasing speed improvements while maintaining sample quality. Furthermore, the exploration of the continuous-time limit offers novel insights into bridging discrete and continuous diffusion model methodologies. The de-randomization aspect of DNDM is a crucial contributor to its acceleration capabilities, making it a notable advancement in the field.
Non-Markov Approach#
A Non-Markov approach to diffusion models offers a compelling alternative to traditional Markov chains. By relaxing the Markov assumption, which stipulates that the next state depends solely on the current state, Non-Markov models can capture long-range dependencies and more complex dynamics. This allows for more efficient sampling procedures and the potential to generate higher-quality samples, as demonstrated by the reduced number of function evaluations needed. The predetermined transition time sets in the Non-Markov framework enable a training-free sampling algorithm, significantly speeding up the process compared to existing Markov methods, as the model avoids redundant computations associated with step-by-step Markov transitions. However, the Non-Markov nature introduces challenges. The absence of the Markov property makes theoretical analysis more intricate, impacting the understanding of the reverse process and optimization strategies. A careful theoretical study is required to ensure the validity and reliability of the Non-Markov process for generating diverse and high-quality samples. Bridging the gap between discrete and continuous-time processes within the Non-Markov framework also presents a fascinating avenue of research.
Transition Time’s Role#
The concept of ‘Transition Time’s Role’ in discrete diffusion models is crucial for understanding and improving the sampling process. Transition time, representing the point at which a token transitions from its original state to pure noise, introduces non-Markovian behavior, enabling faster sampling algorithms. This is because the reverse process only needs to evaluate the neural network at specific transition times, rather than at every time step. The distribution of transition times further shapes the sampling efficiency and sample quality. Predetermining the transition time set allows for a training-free sampling method, significantly accelerating the process. Moreover, analyzing the transition from finite to infinite step sampling, using a continuous schedule, offers valuable insights into bridging discrete and continuous-time diffusion models. In essence, understanding ‘Transition Time’s Role’ is key to advancing discrete diffusion and designing efficient, high-quality sampling procedures.
Continuous-Time Limit#
The continuous-time limit in the context of discrete diffusion models represents a crucial theoretical bridge connecting discrete and continuous-time formulations. It offers insights into how the behavior of a discrete diffusion model changes as the time step size approaches zero, effectively transitioning it to a continuous-time process. This transition is significant as continuous-time diffusion models often possess attractive analytical properties which can simplify inference. By exploring the continuous-time limit, researchers can derive theoretical understanding of the original discrete-time model, potentially uncovering links to continuous-time diffusion’s well-established mathematical framework. This may facilitate developing more efficient sampling algorithms, improving the speed and quality of data generation. It can provide a theoretical justification for certain approximations made in discrete-time models and lead to new algorithms by leveraging results from continuous-time analysis. Furthermore, analyzing this limit can reveal fundamental relationships between continuous and discrete-time frameworks for diffusion models, contributing to a deeper understanding of the underlying mathematical principles and providing a useful perspective when designing new methods or extending existing ones. Finally, comparing the continuous-time limit with the actual performance of finite step sampling might illuminate limitations of certain discrete approximations and guide future methodological developments.
Future Research#
Future research directions stemming from this work could explore several promising avenues. Extending the DNDM framework to other data modalities beyond text, such as images and audio, would significantly broaden its applicability and impact. Investigating the theoretical underpinnings of the transition time set could lead to more efficient sampling algorithms and a deeper understanding of the model’s dynamics. Furthermore, research into alternative noise distributions and the impact on sampling efficiency could yield substantial improvements. Finally, a comparative analysis of DNDM’s performance against other generative models, particularly in resource-constrained settings, is needed to establish its robustness and practical utility.
More visual insights#
More on figures
This figure compares the relationship between generation quality (measured by BLEU score) and computational time for different models on the IWSLT14 dataset. The x-axis represents the computational time in seconds, and the y-axis represents the BLEU score. Each line represents a different sampling algorithm. Steeper slopes indicate a higher improvement in BLEU score per unit of computational time. This figure helps to visualize the efficiency of DNDM in achieving higher BLEU scores with less computational cost compared to baselines.

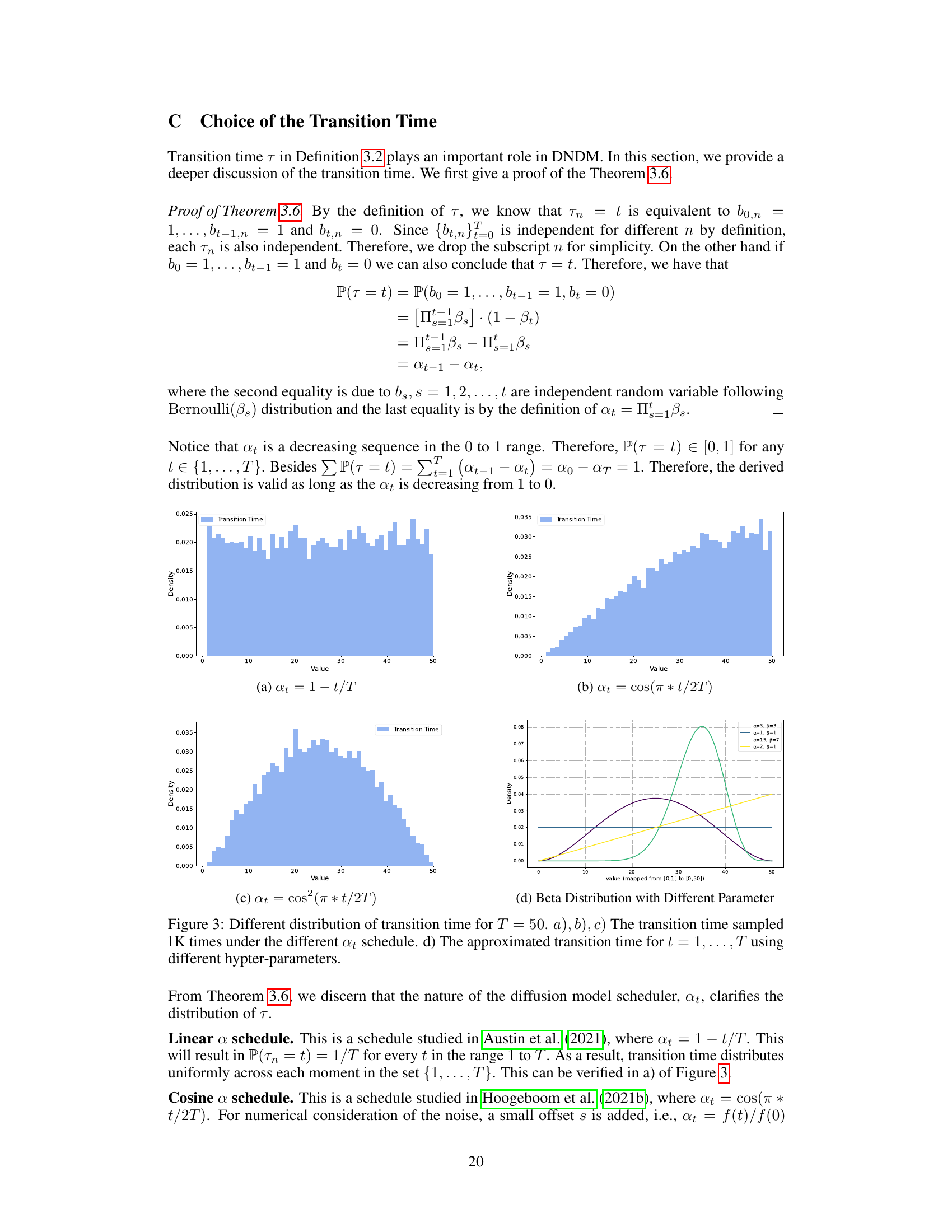
This figure shows the distribution of transition times for different scheduling schemes of at. The transition time is sampled 1000 times for each scheme. The plots (a), (b), and (c) visualize the distribution for the linear schedule (at = 1 - t/T), cosine schedule (at = cos(πt/2T)), and cosine squared schedule (at = cos²(πt/2T)), respectively. Plot (d) illustrates how different Beta distributions can approximate the transition time distributions for the three schedules.
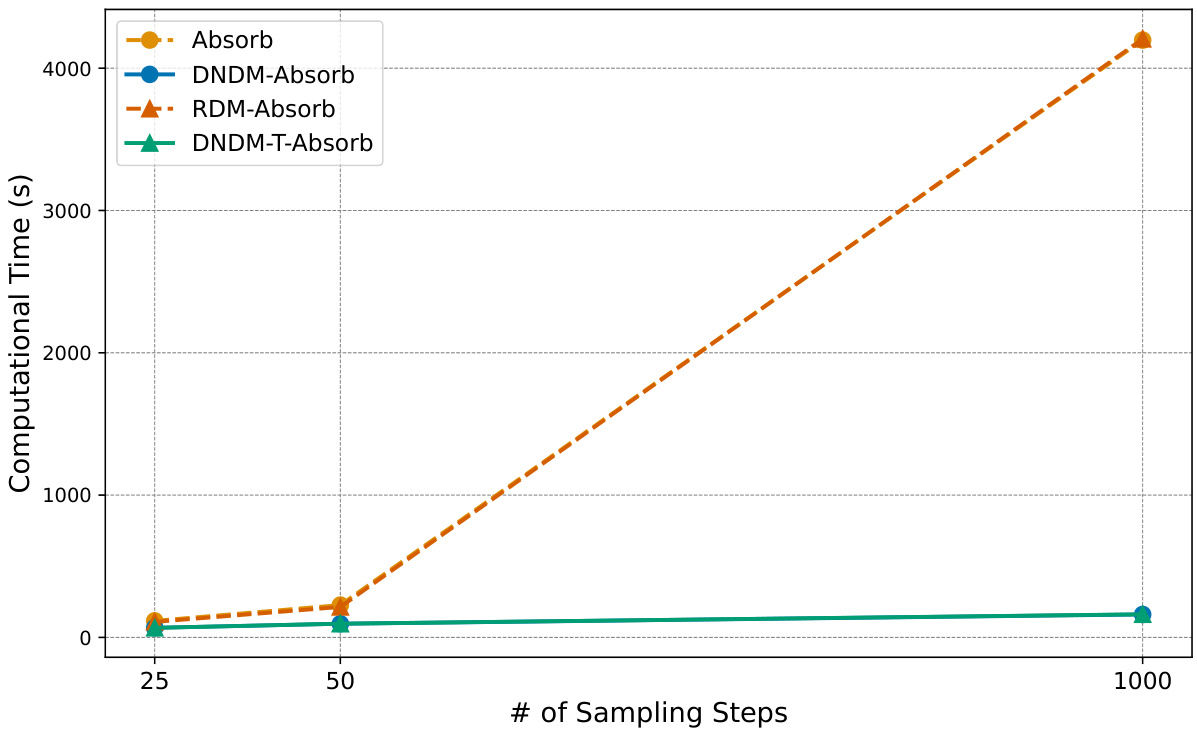
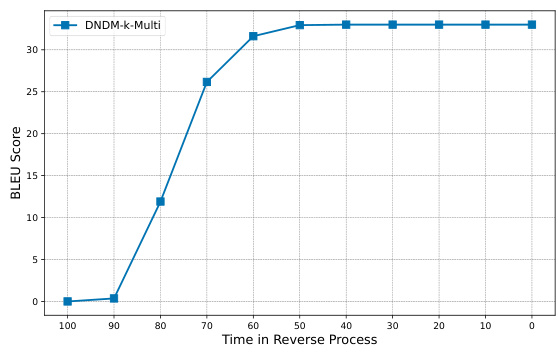
This figure compares the computational time of different methods for absorbing diffusion on the IWSLT14 dataset. It shows that the computational time for the baseline methods (Absorb, RDM-Absorb) increases linearly with the number of sampling steps. In contrast, the proposed DNDM methods (DNDM-Absorb, DNDM-T-Absorb) exhibit significantly less increase in computational time as the number of sampling steps increases. This highlights the efficiency of the DNDM approach in accelerating the sampling process.
More on tables

This table compares the performance of different diffusion models on three machine translation datasets (IWSLT14 DE-EN, WMT14 EN-DE, and WMT16 EN-RO) using the BLEU score as a metric. It shows the performance for different numbers of steps (25, 50, 1000, and ∞ for continuous sampling) and whether top-k selection was used. The blue highlighting indicates the authors’ methods (DNDM), and bold numbers represent the best performance within each row.

This table presents the BLEU scores and the average sampling time in seconds for different models (RDM-Multi, DNDM-Multi, RDM-k-Multi, DNDM-k-Multi) on three machine translation datasets (IWSLT14 DE-EN, WMT14 EN-DE, WMT16 EN-RO) with different numbers of sampling steps (25, 50, 1000, ∞). The results are broken down by whether top-k selection was used during token generation. The table shows the performance of different models and the effect of using top-k selection on BLEU score and sampling speed across different datasets and number of steps.
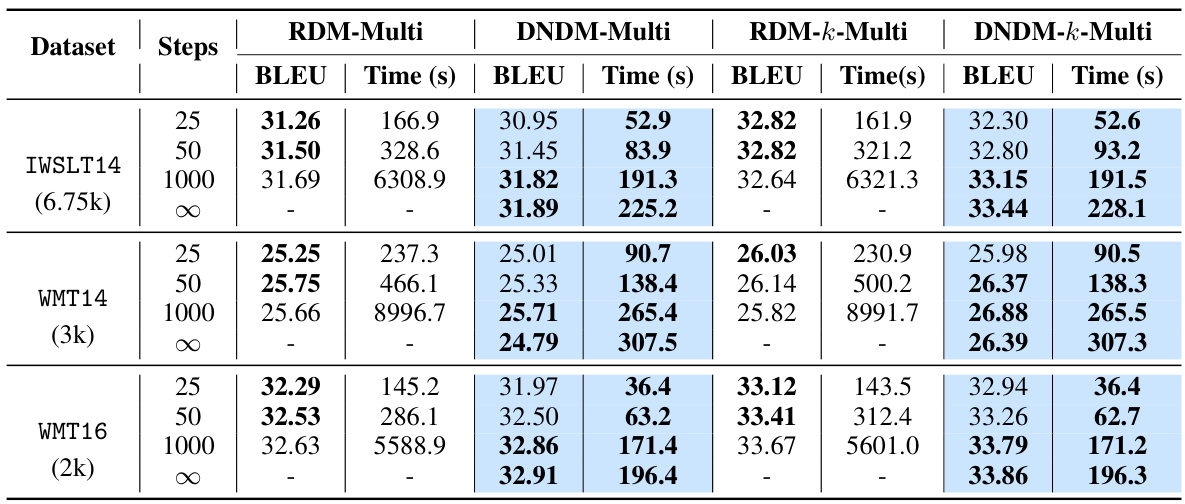
This table presents the BLEU scores and computation times for different diffusion models on three machine translation tasks (IWSLT14 DE-EN, WMT14 EN-DE, and WMT16 EN-RO). It compares the performance of RDM and RDM-k (baselines from Zheng et al., 2023) against DNDM and DNDM-k (the proposed methods). Results are shown for 25, 50, and 1000 sampling steps, as well as the continuous-time limit (∞). The table highlights the superior performance of the DNDM-based models in terms of both speed and sample quality.

This table presents the BLEU scores and the corresponding sampling time for different models (RDM-Multi, DNDM-Multi, RDM-k-Multi, and DNDM-k-Multi) on three machine translation datasets (IWSLT14 DE-EN, WMT14 EN-DE, and WMT16 EN-RO) with different numbers of sampling steps (25, 50, 1000, and ∞). The table highlights the superior performance of the proposed DNDM models in terms of both speed and BLEU score.
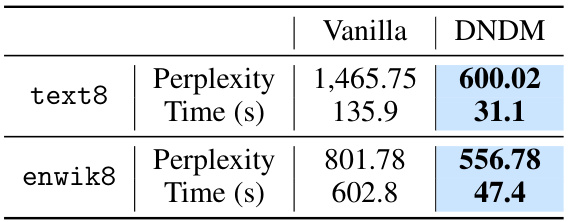
This table presents the results of experiments evaluating the performance of different diffusion models on machine translation tasks. It compares the BLEU scores and computation times for various models (RDM-Multi, DNDM-Multi, RDM-k-Multi, DNDM-k-Multi) across three different datasets (IWSLT14 DE-EN, WMT14 EN-DE, and WMT16 EN-RO) and different numbers of sampling steps (25, 50, 1000). The table highlights the superior performance of the proposed DNDM models in terms of both speed and quality, especially when using a larger number of sampling steps.

This table presents the results of the BLEU score and sampling time for different models (RDM-Multi, DNDM-Multi, RDM-k-Multi, DNDM-k-Multi) on three machine translation datasets (IWSLT14 DE-EN, WMT14 EN-DE, WMT16 EN-RO) with different numbers of steps (25, 50, 1000, ∞). The results show the performance of both multinomial diffusion and the proposed methods (DNDM) across various settings, including with and without top-k selection.
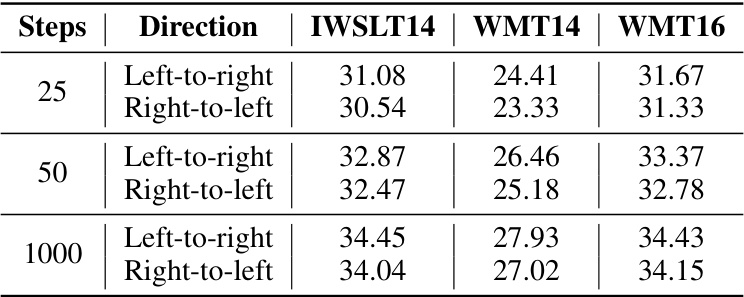
This table presents the BLEU scores achieved using two different transition approaches (left-to-right and right-to-left) for machine translation tasks on three different datasets (IWSLT14, WMT14, and WMT16) with varying numbers of sampling steps (25, 50, and 1000). The left-to-right approach shows better results.

This table presents the BLEU scores and the average time in seconds for different sampling steps (25, 50, 1000, and ∞) using multinomial diffusion on three machine translation datasets (IWSLT14 DE-EN, WMT14 EN-DE, and WMT16 EN-RO). It compares the performance of four different methods: RDM-Multi, DNDM-Multi, RDM-k-Multi, and DNDM-k-Multi. The results show the impact of the number of sampling steps and the use of top-k selection on BLEU score and sampling speed.

This table presents the BLEU scores and average sampling times for different diffusion models on three machine translation tasks (IWSLT14 DE-EN, WMT14 EN-DE, and WMT16 EN-RO). It compares the performance of RDM and RDM-k (from Zheng et al., 2023) with DNDM and DNDM-k for different numbers of sampling steps (25, 50, 1000) and in the continuous-time limit. The results show the impact of the proposed DNDM method on both sampling speed and the quality of the generated translations.
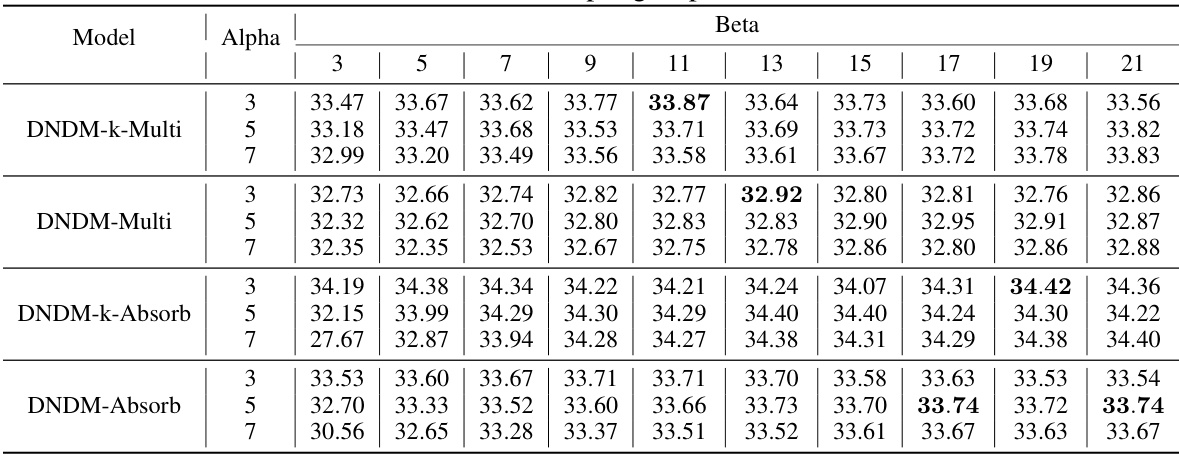
This table presents the BLEU scores and sampling times for different models (RDM-Multi, DNDM-Multi, RDM-k-Multi, DNDM-k-Multi) on three machine translation datasets (IWSLT14 DE-EN, WMT14 EN-DE, WMT16 EN-RO) with varying numbers of sampling steps (25, 50, 1000). The best BLEU score for each row is bolded, highlighting the effectiveness of the proposed DNDM approach in improving both the speed and the quality of machine translation.
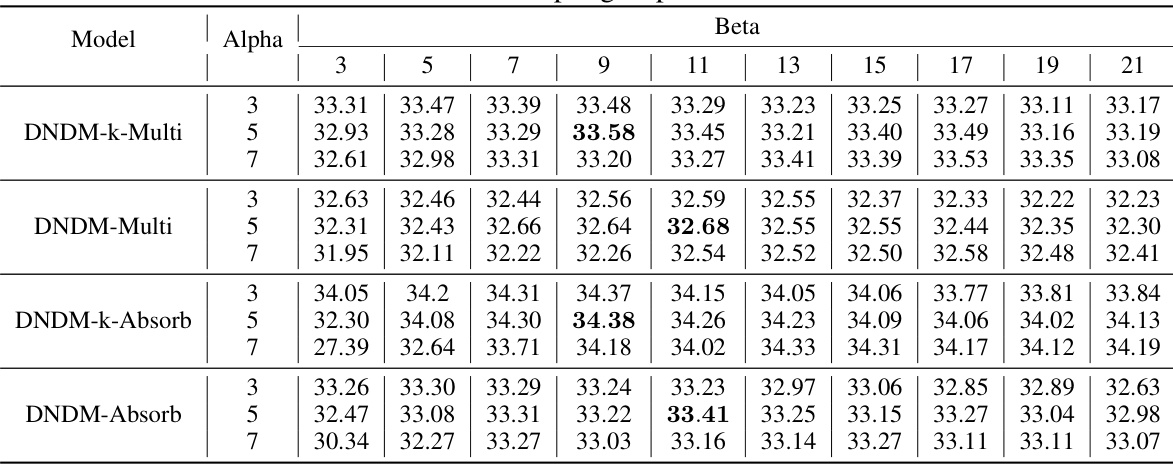
This table presents the BLEU scores and inference times for different models on three machine translation datasets (IWSLT14 DE-EN, WMT14 EN-DE, and WMT16 EN-RO) using multinomial diffusion. It compares the performance of RDM (baseline) and DNDM models with different numbers of sampling steps (25, 50, 1000, and ∞). The table highlights the superior performance of DNDM in terms of both speed and BLEU scores.

This table presents the BLEU scores and the average number of function evaluations (NFE) for different models (RDM-Absorb, DNDM-Absorb, RDM-k-Absorb, DNDM-k-Absorb) on three machine translation datasets (IWSLT14 DE-EN, WMT14 EN-DE, and WMT16 EN-RO). The results are shown for 25, 50, and 1000 steps, and the best results for each setting are highlighted in bold. The table shows that DNDM-based methods generally outperform RDM-based methods, particularly for a large number of steps (1000). The table also presents results for continuous-time sampling (∞ steps).
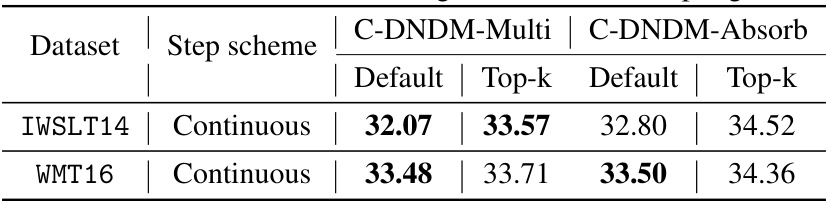
This table presents the BLEU scores and inference times for different models on three machine translation tasks using multinomial diffusion. The models compared are RDM-Multi, RDM-k-Multi, DNDM-Multi, and DNDM-k-Multi, with varying numbers of steps (25, 50, 1000, and ∞). The table shows that DNDM models generally achieve higher BLEU scores and significantly faster inference times than RDM models, particularly with a larger number of steps.

This table presents the BLEU scores and inference times for different models on three machine translation tasks using multinomial diffusion. It compares the performance of RDM (a baseline) and DNDM (the proposed method) with and without top-k selection for various numbers of sampling steps (25, 50, 1000). The results highlight the speed improvement and comparable quality of DNDM, especially at higher sampling steps.
Full paper#