On the Robustness of Spectral Algorithms for Semirandom Stochastic Block Models

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on graph partitioning and community detection. It significantly advances our understanding of spectral algorithms’ robustness against various adversarial attacks, particularly in semirandom models. The findings are relevant to various real-world network applications and suggest potential improvements in algorithm design, offering new avenues for research in algorithm robustness and model mis-specification.

Visual Insights

#

This figure presents a comprehensive analysis of the performance of different spectral algorithms for graph bisection in a non-homogeneous stochastic block model. It shows the agreement of different bipartition methods (0-cut and sweep cut) with the planted bisection for varying probabilities, and the embedding variance of the second eigenvector. The results reveal a surprising difference in the robustness of spectral bisection when considering normalized versus unnormalized Laplacians.

This table shows the block structure of the expected adjacency matrix A* used in the proof of Theorem 3. The matrix is partitioned into four blocks representing the communities L1, L2, and R (as defined in the paper). The entries within each block represent the probabilities that edges exist between the vertices in the corresponding communities. The values K, p, and q are parameters of the model, with K indicating a higher edge probability within L1 and L2 compared to between L1 and L2, or between L and R.

In-depth insights

#

Spectral Robustness

#

Spectral robustness in graph partitioning investigates how well spectral clustering algorithms, which rely on eigenvectors of graph matrices like the Laplacian, withstand deviations from idealized models. The core challenge is that real-world graphs are often messy, exhibiting properties not captured in clean theoretical models like the Stochastic Block Model (SBM). Robustness studies examine how spectral methods perform under various forms of adversarial perturbations or noise, evaluating their ability to correctly recover the underlying community structure. A key focus is on determining which graph properties (e.g., spectral gaps, degree distributions) are crucial for maintaining accuracy, and how different variants of spectral clustering (normalized vs. unnormalized Laplacian) fare under these conditions. The findings often reveal surprising contrasts: some algorithms prove surprisingly resilient to certain types of noise, while others are extremely sensitive. Understanding spectral robustness helps us design more reliable graph partitioning methods and better interpret results in real-world applications where data imperfections are unavoidable.

Semi-random Models

#

Semi-random models offer a powerful framework for analyzing the robustness of algorithms by bridging the gap between average-case and worst-case scenarios. They introduce a controlled level of adversarial manipulation, allowing for a nuanced understanding of algorithm behavior beyond the idealized assumptions of purely random models. The key advantage lies in the ability to inject helpful, yet controlled, perturbations that might arise in real-world data without completely obliterating the underlying structure. This approach allows for a more accurate assessment of an algorithm’s true capabilities and limitations, revealing its resilience against realistic deviations from the ideal model. Semirandom models are especially valuable for evaluating the performance of spectral clustering algorithms, which are known to be sensitive to even slight model misspecifications. By using semi-random models, one can systematically assess the algorithm’s resilience to noisy or biased data, ultimately providing a more trustworthy evaluation than relying solely on fully random models.

Laplacian Variants

#

The concept of “Laplacian Variants” in graph-based spectral clustering methods is crucial. It centers on the choice between the unnormalized Laplacian (L) and the normalized Laplacian (Lsym). The unnormalized Laplacian, simpler to compute, directly reflects the graph’s structure through degree differences. However, its performance can be heavily influenced by degree variations, impacting its robustness to noise and model misspecifications. Conversely, the normalized Laplacian, by incorporating degree information into its calculation, exhibits improved robustness to such irregularities. It often leads to better clustering performance in graphs with significant degree heterogeneity. The choice between these variants becomes a critical consideration depending on the specific characteristics of the data, the presence of noise, and the desired level of robustness against model mismatches. This selection significantly impacts the algorithm’s ability to accurately recover community structures. Theoretical analyses show a stark contrast in the robustness of spectral algorithms using each variant against various adversarial attacks. Specifically, the unnormalized Laplacian shows strong consistency under certain semirandom adversarial models, while the normalized Laplacian fails in the same settings. Therefore, the choice between Laplacian variants is not a matter of simple preference, but rather a critical design decision significantly impacting the performance and reliability of spectral clustering methods.

Adversarial Insights

#

Adversarial attacks and defenses are critical in evaluating the robustness of machine learning models. In the context of spectral graph clustering, an adversarial approach reveals crucial insights into algorithm behavior. Semirandom adversaries, which can modify the input graph in ways consistent with the ground-truth community structure, provide a more nuanced evaluation than standard random graph models. By analyzing how spectral clustering algorithms perform under such attacks, we can better understand their limitations and identify areas of overfitting to statistical assumptions. This helps clarify the differences in the robustness of spectral algorithms utilizing normalized versus unnormalized Laplacians, showing the unexpected strength of the unnormalized approach in specific adversarial scenarios. The study of these adversarial examples highlights the importance of moving beyond standard model assumptions towards a more comprehensive understanding of algorithm vulnerabilities in real-world settings. These insights are not limited to graph clustering, and understanding algorithm weaknesses under various adversarial modifications can improve the overall robustness and reliability of machine learning methods.

Future Directions

#

The “Future Directions” section of this research paper would ideally explore several promising avenues. Extending the semirandom models to encompass a broader range of adversarial modifications is crucial. This could involve investigating different types of edge alterations beyond simple additions and focusing on how these impact the robustness of various spectral algorithms. A deeper analysis of the normalized Laplacian’s failure modes is warranted. The surprising inconsistency observed in the paper necessitates further research to determine underlying reasons and potential mitigations. Comparing various spectral methods under different adversarial attacks would provide a more comprehensive understanding of their strengths and weaknesses. Finally, exploring the theoretical limits of spectral methods for graph partitioning, particularly their information-theoretic thresholds, could inform future algorithm design and provide concrete performance bounds. The study could also investigate the applicability and effectiveness of spectral clustering in various real-world scenarios beyond graph bisection. Empirically validating these theoretical findings using large-scale datasets representative of real-world networks is paramount to assessing their practical significance.

More visual insights

#

More on figures

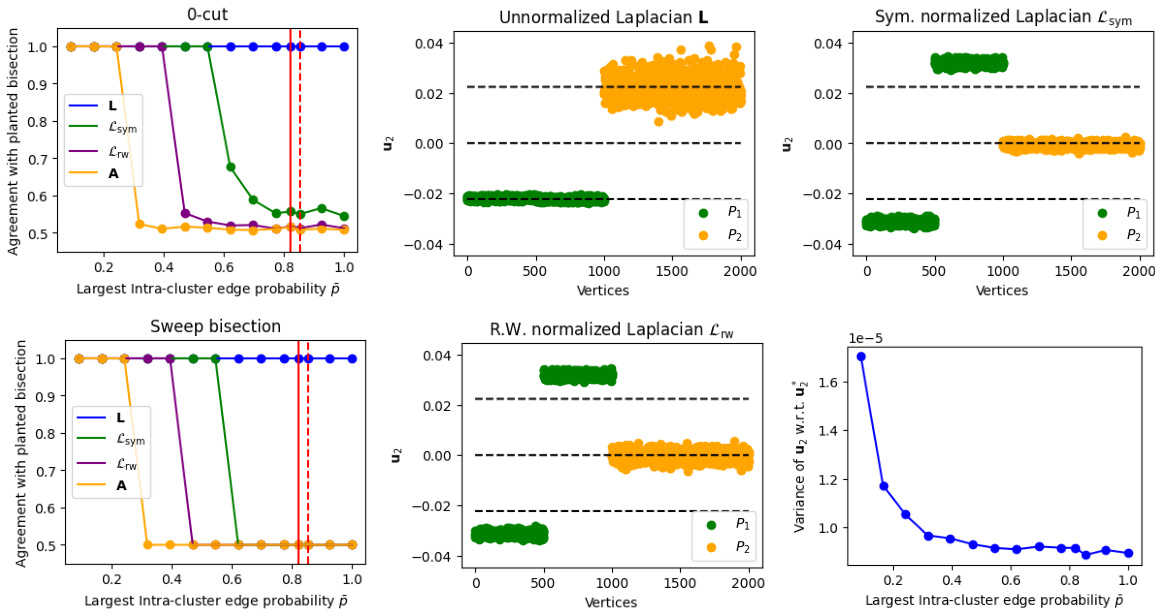
The figure shows the results of numerical experiments on the performance of different spectral clustering algorithms under various parameter settings. The top-left and bottom-left plots compare the accuracy of different bisection methods (0-cut and sweep cut) for different values of p. The top-middle, top-right, and bottom-middle plots visualize the embedding of vertices using the second eigenvector of different matrices. The bottom-right plot illustrates the variance of the embedding from the unnormalized Laplacian’s second eigenvector.

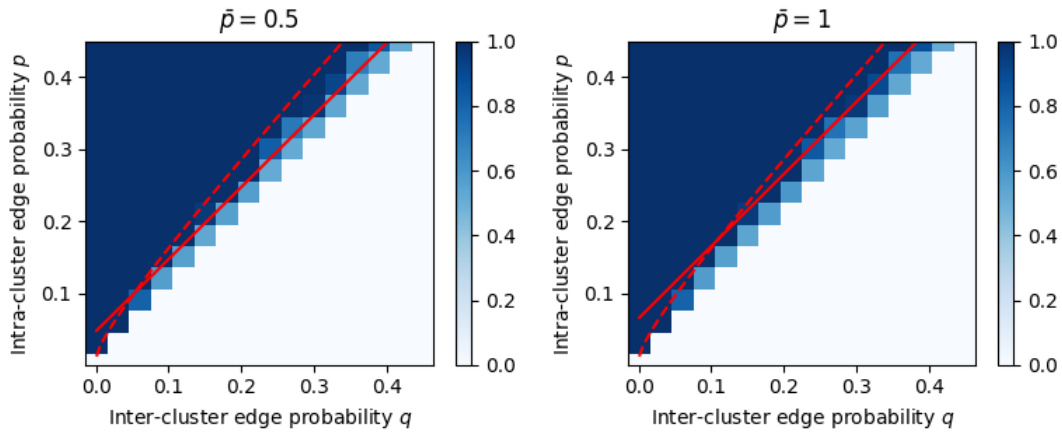
This figure shows the results of an experiment where the authors tested the performance of unnormalized spectral bisection on graphs generated from a non-homogeneous symmetric stochastic block model (NSSBM). They varied the intra-cluster edge probability (p) while keeping the inter-cluster edge probability (q) fixed. The plots show the agreement between the algorithm’s output and the true community structure. The solid red curves represent a theoretical threshold (Pthr) derived from Theorem 1, below which exact recovery is not guaranteed. The dashed red curves show the information-theoretic threshold (Pinfo) for exact recovery, which is a lower bound on the performance of any algorithm.

The figure shows the performance of different spectral algorithms (using unnormalized Laplacian, symmetric normalized Laplacian, random walk normalized Laplacian, and adjacency matrix) on a deterministic cluster model (DCM) when the size of the planted clique varies. The left panel displays the agreement (fraction of correctly classified vertices) using a 0-cut method, while the right panel uses a sweep cut method. The results show the agreement with the planted bisection for each algorithm.

This figure shows the minimum in-cluster degree and the spectral gap for various sizes of a planted clique in the deterministic cluster model. The red horizontal lines represent theoretical lower bounds from Theorem 2, indicating the conditions for strong consistency of the unnormalized spectral bisection algorithm. The plot illustrates how these parameters change as the planted clique size varies and how they relate to theoretical expectations.

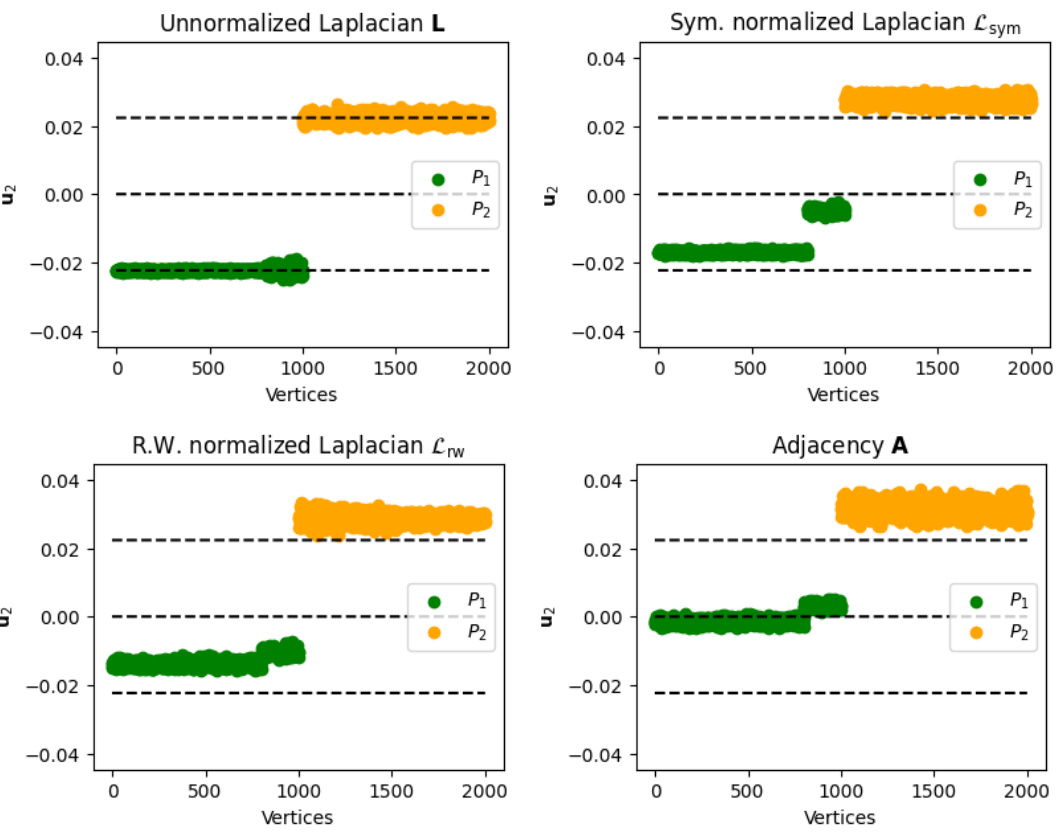
This figure shows the embedding of vertices by the second eigenvector (u2) of four different matrices (Unnormalized Laplacian, Symmetric Normalized Laplacian, Random Walk Normalized Laplacian, and Adjacency Matrix) for a graph sampled from the Deterministic Clusters Model (DCM). The size of the planted clique is set to 2/5n. The plot helps visualize how well each matrix’s eigenvector separates the vertices into the two communities (P1 and P2), with horizontal lines at ±1/√n and 0 as reference points. The visualization is useful for comparing the performance of different spectral clustering methods under the DCM.

Full paper

#