Oracle-Efficient Reinforcement Learning for Max Value Ensembles

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it presents a novel, scalable algorithm for reinforcement learning in large state spaces. This addresses a major challenge in the field by leveraging existing base policies rather than learning from scratch. The algorithm’s efficiency and theoretical guarantees are significant contributions, opening new avenues for research and practical applications.

Visual Insights

#

This figure shows two examples of Markov Decision Processes (MDPs). The first MDP (a) illustrates a scenario where two policies, one always going left and the other always going right, each yield low cumulative rewards individually. However, a max-following policy (which, at each state, selects the action yielding the highest expected cumulative reward from among the base policies) would achieve optimal performance by cleverly switching between left and right actions at appropriate times. The second MDP (b) highlights that max-following policies may not always be optimal, and different max-following policies can have different values, depending on how ties are broken between equally valued actions. This example shows that the max-following policy can be arbitrarily worse than an optimal policy depending on the starting state.

This table lists the hyperparameters used in the MaxIteration algorithm. These include optimizer settings (Adam), learning rates for the value function, the number of rounds and gradient steps per round, batch size, and the discount factor (γ). These settings are crucial for the performance of the algorithm in the experiments.

In-depth insights

#

Max Ensemble RL

#

Max Ensemble Reinforcement Learning (RL) presents a novel approach to tackling the challenges of RL in large or infinite state spaces. Instead of directly seeking an optimal policy, it leverages a collection of pre-existing base policies, possibly heuristic or suboptimal, to construct a superior policy. The core idea is to compete with a max-following policy, which at each state selects the action suggested by the best-performing base policy. This approach is attractive because it bypasses the computationally expensive process of learning value functions and optimal policies from scratch in high-dimensional spaces. The key contribution often involves an efficient algorithm that learns a policy competitive with the max-following policy, requiring only access to an empirical risk minimization (ERM) oracle for the base policies’ value function approximations, rather than needing access to the max-following policy’s value function directly. This makes the approach scalable and practically viable. The theoretical guarantees often rely on minimal assumptions about the ERM oracle and the samplability of state distributions, reducing the computational burden significantly. However, the algorithm’s success is still linked to the quality of the base policies, and the practical performance is affected by the accuracy of value function approximations provided by the oracle, which is crucial for successful state selection.

Oracle-Efficient RL

#

Oracle-efficient reinforcement learning (RL) tackles the challenge of scaling RL algorithms to large or infinite state spaces. Traditional RL methods often struggle with computational complexity that scales with the state space size, rendering them impractical for real-world applications. Oracle-efficient RL addresses this by leveraging access to an ‘oracle,’ typically a value function approximator. This oracle allows the algorithm to efficiently estimate value functions without explicitly exploring the entire state space. The key is that the oracle’s queries are limited, often to efficiently samplable distributions. The focus shifts from directly learning optimal policies to learning policies that compete with, for example, a max-following policy constructed from simpler base policies. This approach drastically reduces the computational burden while retaining strong theoretical guarantees. Oracle-efficient RL represents a significant step towards making RL applicable to complex, high-dimensional problems in robotics and other domains where exploration is costly and full state-space coverage is infeasible.

Maxlteration Algo

#

The Maxlteration algorithm, a core contribution of the research paper, presents an efficient approach to learn a policy that performs competitively with the best of a set of given base policies. It cleverly addresses the challenge of reinforcement learning in large or infinite state spaces by leveraging the value function information from constituent policies without needing to directly learn the value function of the optimal or max-following policy. This incremental learning approach iteratively constructs an improved policy over the time steps of an episode. The algorithm’s efficiency stems from its oracle-efficient design, querying a value function approximation oracle only on samplable distributions, thus scaling favorably to complex scenarios. The theoretical guarantees provided show the competitive nature of the policy learned by Maxlteration with the approximate max-following policy, proving its efficacy under relatively weak assumptions. Furthermore, empirical results on robotic simulation testbeds demonstrate its practical effectiveness and highlight cases where Maxlteration surpasses the individual constituent policies significantly.

Benchmark Analysis

#

A robust benchmark analysis is crucial for evaluating reinforcement learning algorithms. It should go beyond simply comparing performance against existing methods; instead, it should critically examine the chosen benchmark’s suitability and limitations. This involves considering the properties of the benchmark environment: Does it accurately reflect real-world scenarios or is it overly simplified? What are its inherent biases, and how might these affect the conclusions drawn? Furthermore, a comprehensive analysis would explore the algorithm’s performance across diverse variations of the benchmark environment. Analyzing sensitivity to parameter changes and other factors helps determine an algorithm’s robustness and generalizability. A strong benchmark analysis also accounts for computational resources: A method that outperforms others but requires significantly more computing power may not be practical. Ultimately, a truly insightful benchmark analysis leads to a deeper understanding of the algorithm’s strengths and weaknesses, improving algorithm design and enabling more informed choices in real-world applications.

Future of Max RL

#

The future of Max RL hinges on addressing its current limitations and exploring new avenues. Improving the efficiency and scalability of Max RL algorithms is crucial, potentially through refined value function approximation techniques, and novel optimization strategies. Weakening reliance on strong oracle assumptions is key, enabling applicability to broader real-world scenarios. Investigating the theoretical properties of Max RL in more depth is needed, particularly concerning its convergence guarantees, and the relationship between the quality of constituent policies and the overall performance of the Max RL agent. Exploring variations on the Max RL approach, such as using soft-max aggregation, or other ensemble methods, could offer improved robustness and performance. Finally, applying Max RL to increasingly complex domains like robotics and game playing, while considering safety and fairness implications, is essential for demonstrating its practical utility and furthering its development.

More visual insights

#

More on figures

This figure shows two examples of Markov Decision Processes (MDPs) to illustrate the performance of max-following policies compared to optimal policies and individual constituent policies. The first MDP (a) demonstrates a scenario where two policies (one going left, one going right) perform poorly individually, but a max-following policy combining them achieves optimality. The second MDP (b) highlights cases where max-following policies can be significantly worse than the optimal policy depending on the starting state and how ties are broken between policies.

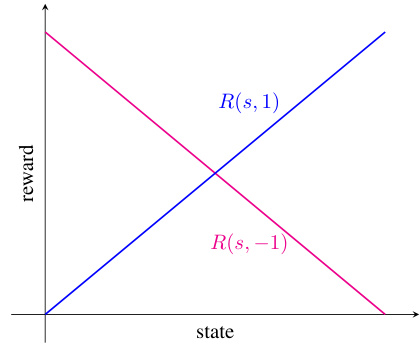
This figure consists of two subfigures. Subfigure (a) shows an MDP where small value approximation errors at s0 hinder max-following. The transition dynamics are color-coded to indicate actions taken by π⁰ (red) and π¹ (blue). Subfigure (b) shows an MDP where the max-following value function is piecewise linear, unlike the constituent policy values which are affine functions of the state for fixed actions.

This figure compares the performance of Maxlteration against IQL fine-tuning on three different robotic manipulation tasks from the CompoSuite benchmark. For each task, two pre-trained policies (Policy 0 and Policy 1) serve as input to Maxlteration. The figure displays the mean return and success rate for each method across five independent runs, with error bars representing the standard error. The results show that Maxlteration sometimes outperforms IQL fine-tuning in terms of return, but this increased return does not always translate into higher success rates.

This figure shows the experimental results comparing MaxIteration’s performance against fine-tuning IQL on several robotic manipulation tasks from the CompoSuite benchmark. Each pair of bars represents a different task, with the constituent policies trained using IQL on simpler subtasks. The figure compares the mean return and success rate of Maxlteration with IQL’s fine-tuning capabilities. The error bars represent the standard error across five trials. Maxlteration often improves returns over the base IQL policies but doesn’t always improve success rates; highlighting that improved returns do not guarantee improved task success.

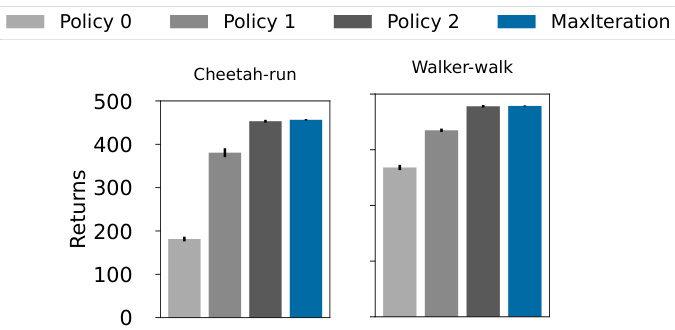
This figure shows the results of the MaxIteration algorithm on two tasks from the DeepMind Control Suite: Cheetah-run and Walker-walk. The algorithm is tested against three constituent policies (Policy 0, Policy 1, Policy 2) and compared to the results of using only the best performing constituent policy. The error bars represent the standard error across five different runs. The key finding is that MaxIteration consistently selects and performs as well as the best of the three constituent policies.

More on tables

This table lists the hyperparameters used in the MaxIteration algorithm. These include the optimizer used (Adam), its associated hyperparameters (beta1, beta2, epsilon), the learning rate for the value function, the number of rounds for the algorithm, the number of gradient steps per round, the batch size, and the gamma discount factor.

This table lists the hyperparameters used for the Implicit Q-Learning algorithm in the paper’s experiments. It includes settings for the Adam optimizer (beta1, beta2, epsilon), learning rates for both the actor and critic networks, batch size, n_steps, gamma (discount factor), tau (soft update parameter), number of critics, and parameters related to the algorithm’s quantile regression function (expectile, weight_temp, max_weight). These hyperparameters are crucial for the algorithm’s performance and reproducibility.

Full paper

#