↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Online multi-group learning aims to create algorithms that perform well on various subsets (groups) of data. Existing methods often struggle with computationally expensive enumeration when dealing with many or overlapping groups, hindering their practicality for large-scale applications. The challenge is to design efficient algorithms that avoid explicitly checking all groups. This is crucial especially in fairness applications where considering numerous demographic attributes can lead to an explosion in the number of groups.
This paper introduces novel oracle-efficient algorithms that elegantly circumvent the enumeration problem. Instead of explicitly checking every group, these algorithms utilize optimization oracles to access groups implicitly. This makes them computationally feasible even for extremely large datasets, a substantial improvement over existing methods. The study proves that these algorithms achieve sublinear regret under diverse conditions (i.i.d., smoothed adversarial and adversarial transductive settings), demonstrating their robustness and efficacy in different contexts.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on online learning and fairness in machine learning. It presents novel, computationally efficient algorithms that achieve sublinear regret in various settings, even when dealing with a massive number of groups. This opens up new avenues for addressing fairness concerns in large-scale online applications while tackling the computational challenges associated with handling huge datasets.
Visual Insights#
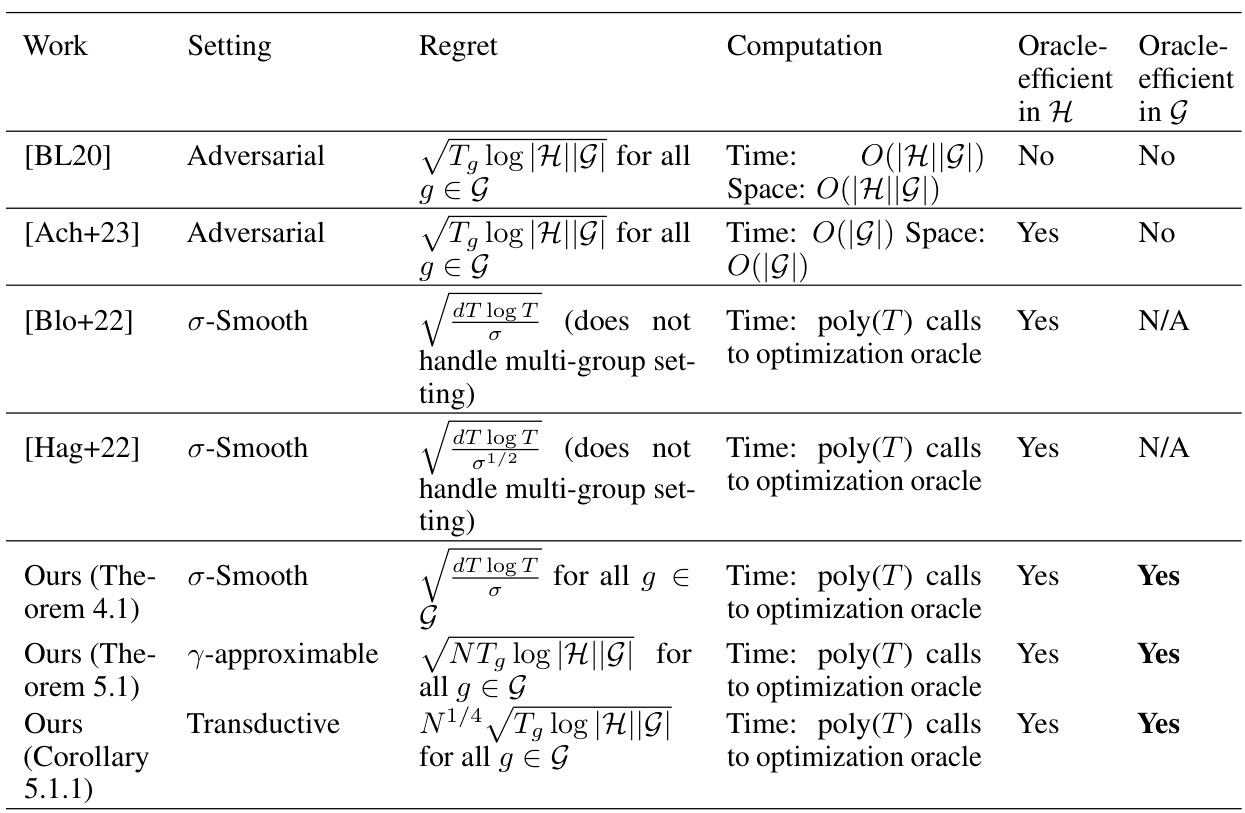
This table summarizes the regret bounds, computational complexity, and oracle efficiency of various online multi-group learning algorithms, including existing algorithms from the literature and the proposed algorithms from this paper. It compares the algorithms across different settings: adversarial, σ-smooth, and transductive. The table highlights the oracle efficiency of the proposed algorithms in both the hypothesis class H and the collection of groups G.
Full paper#



















