↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Deep reinforcement learning (RL) often suffers from sample inefficiency and brittleness, limiting its practical applications. Current approaches like independent and multi-task training struggle to balance efficiency and generalization performance across diverse tasks. The high cost of training makes strategic task selection crucial but poorly understood.
This paper introduces Model-Based Transfer Learning (MBTL), a novel framework to address this challenge. MBTL models generalization performance using Gaussian processes and a linear function of contextual similarity, combining these insights within a Bayesian optimization framework to select training tasks. The results demonstrate up to 50x improved sample efficiency compared to traditional methods across urban traffic and continuous control benchmarks, highlighting MBTL’s effectiveness and robustness.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in reinforcement learning because it addresses the critical issue of sample inefficiency and brittleness in deep RL. By introducing a novel model-based transfer learning framework (MBTL), it offers a significant improvement in sample efficiency (up to 50x) and paves the way for more reliable and scalable deep RL solutions in various domains. The theoretical analysis and empirical results of MBTL provide valuable insights into the problem of generalization in contextual RL, opening exciting avenues for future investigation.
Visual Insights#
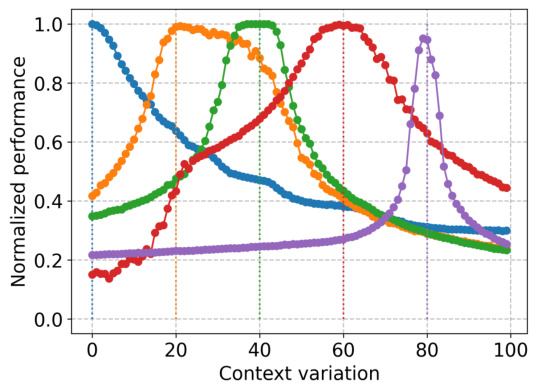
This figure illustrates the concept of generalization gap in contextual Markov Decision Processes (CMDPs). It shows how the performance of a policy trained on one task (source task) degrades as the target task becomes more different from the source task. The solid lines represent the true performance of zero-shot transfer (applying a policy trained on a source task directly to a target task without adaptation), and the dotted lines show the performance of policies trained on different source tasks. The generalization gap increases as the target task becomes less similar to the source task.
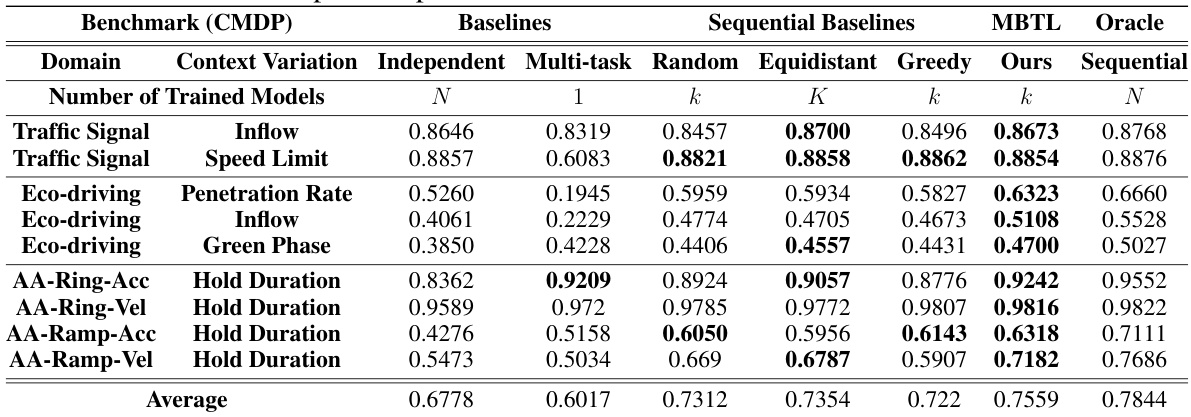
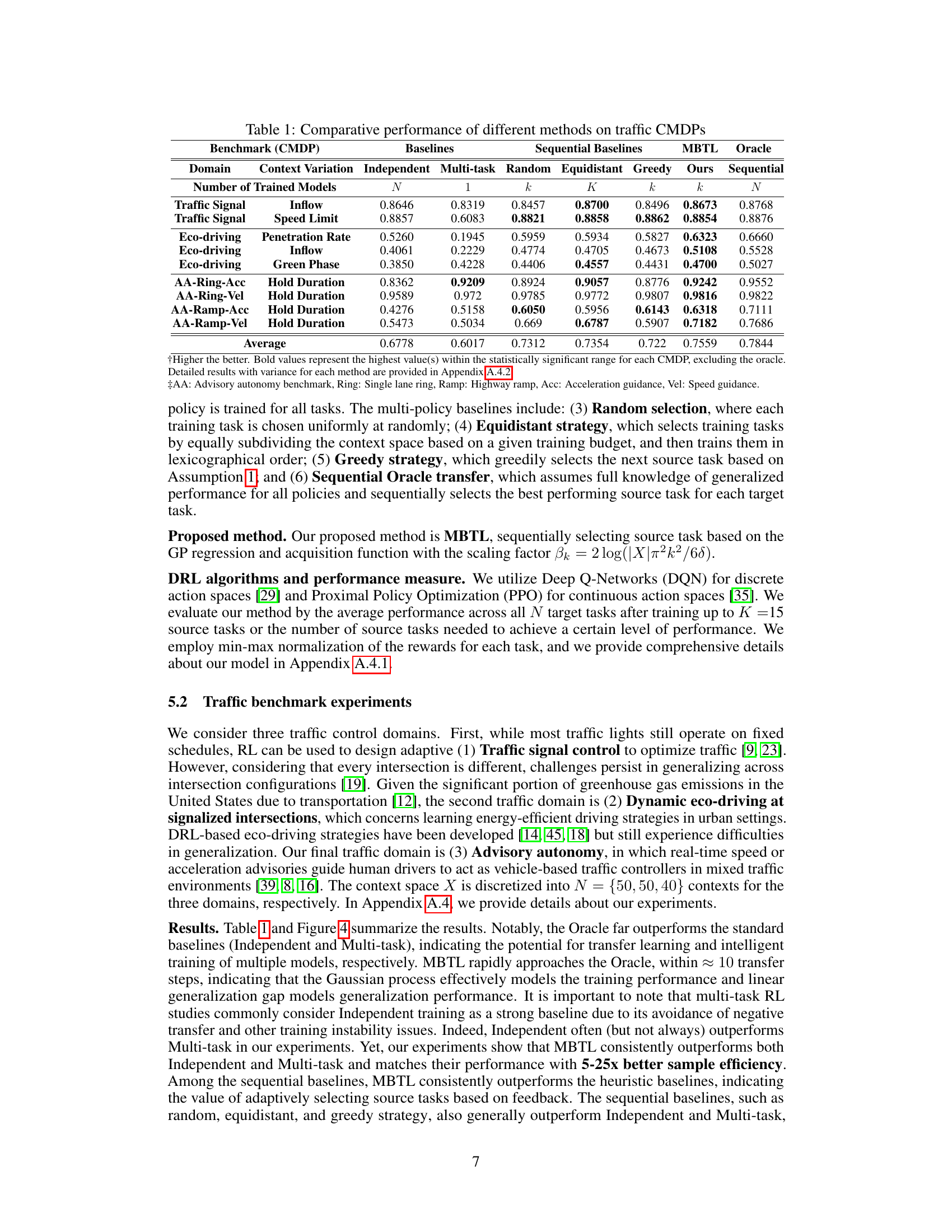
This table compares the performance of various methods for solving contextual Markov Decision Processes (CMDPs) in traffic control tasks. It shows the average normalized performance across different traffic control domains (Traffic Signal, Eco-driving, Advisory Autonomy) and their respective context variations (e.g., inflow, speed limit, penetration rate). The baselines include Independent training (training separate models for each task) and Multi-task learning (training a single model for all tasks). Sequential baselines include randomly selecting tasks, selecting tasks equidistantly across context space, a greedy task selection strategy, and an oracle method (Sequential Oracle transfer, which knows the optimal task selection). The proposed method, MBTL (Model-Based Transfer Learning), is also shown. Higher scores indicate better performance.
In-depth insights#
MBTL Framework#
The Model-Based Transfer Learning (MBTL) framework is a novel approach to contextual reinforcement learning that strategically selects training tasks to maximize generalization performance. It explicitly models generalization performance in two key parts: 1) the performance set point, estimated using Gaussian processes; and 2) the generalization gap (performance loss), modeled as a function of contextual similarity. This two-pronged approach allows MBTL to leverage Bayesian optimization to efficiently select the most informative training tasks, leading to a significant improvement in sample efficiency. A key strength lies in its theoretical grounding, demonstrated by the proof of sublinear regret, which ensures that the algorithm performs well even with a limited number of training tasks. The experimental results across various benchmark tasks provide strong empirical support for the framework’s effectiveness, demonstrating improvements in sample efficiency of up to 50x compared to traditional methods. The framework’s adaptability and insensitivity to specific RL algorithms also showcase its robustness and wide applicability in contextual reinforcement learning problems.
Regret Bounds#
Regret bounds, in the context of sequential decision-making problems like the sequential source task selection problem analyzed in this paper, quantify the difference between the cumulative reward obtained by an algorithm and the optimal cumulative reward achievable. A tighter regret bound indicates better performance, implying that the algorithm’s decisions are closer to optimal choices. The paper’s theoretical contribution focuses on proving sublinear regret for the proposed Model-Based Transfer Learning (MBTL) algorithm. This means the algorithm’s cumulative regret grows slower than the number of decisions made. The analysis further explores conditions under which the regret bounds can be further tightened, potentially leading to even better performance guarantees. This is achieved through the strategic reduction of the search space, which is particularly important when computational resources are limited. The theoretical findings provide a strong foundation for understanding the efficiency and optimality of the MBTL method. The sublinear regret results, along with the analysis of conditions for tighter bounds, significantly strengthen the claim that MBTL is a computationally efficient and effective approach to improve generalization performance in contextual reinforcement learning.
Traffic CMDPs#
The paper explores the application of model-based transfer learning to solve complex decision-making problems within the context of urban traffic management. Traffic CMDPs, or contextual Markov Decision Processes for traffic, provide a structured framework to model the variability and complexity inherent in real-world traffic scenarios. By parameterizing the CMDP with context variables (e.g., road length, inflow rate, speed limits), the authors create a range of tasks that differ in ways that might affect how well a trained reinforcement learning (RL) agent generalizes. The model-based approach allows for efficient exploration of this context space, selecting training tasks strategically to maximize the generalization performance of the learned policies. Key contributions include the introduction of a novel framework that explicitly models generalization performance, theoretical analysis showing sublinear regret, and empirical validation demonstrating significant sample efficiency improvements (up to 50x) compared to standard training methods. The focus is on within-domain generalization, meaning that tasks involve similar settings, but vary in parameters, making it suitable for traffic control. The effectiveness of this method is examined through several real-world traffic benchmarks, demonstrating its potential for improving the efficiency and robustness of RL-based traffic control systems.
Control Benchmarks#
In evaluating reinforcement learning (RL) algorithms, control benchmarks serve as crucial tools. They offer standardized, well-defined tasks to compare the performance of different RL approaches. These benchmarks allow researchers to assess not only the sample efficiency (how much data is needed to achieve a certain level of performance) but also the generalization ability of algorithms across various conditions. The choice of benchmarks is important, reflecting the complexity and realism of the problem being addressed. Simple benchmarks might focus on basic control tasks, enabling quick assessment of core RL capabilities. However, more complex benchmarks with multiple interacting factors provide a more robust test of algorithms, revealing their limitations in realistic settings and ultimately driving the development of more advanced and adaptable RL techniques. Careful selection of diverse benchmarks is key for a thorough evaluation, considering both simpler and more challenging environments to gauge the strengths and weaknesses of an algorithm under different conditions.
Future Work#
The authors mention exploring high-dimensional context spaces and out-of-distribution generalization as important future directions. This suggests a need to scale the model to handle more complex real-world scenarios where multiple factors influence task variations. Addressing the limitations of the linear generalization gap assumption is also highlighted, suggesting a move towards more sophisticated models that capture nonlinear relationships in performance. Further investigation into more robust and principled model-based methodologies for contextual RL is suggested, potentially using different modeling techniques or expanding on the Bayesian optimization framework employed. Finally, developing new real-world CMDP benchmarks is identified to facilitate further research and comparison of different contextual reinforcement learning approaches. This highlights the need for improved generalization across diverse, challenging environments that more accurately represent real-world applications of this technique.
More visual insights#
More on figures

This figure illustrates the Model-Based Transfer Learning (MBTL) algorithm. Panel (a) shows how Gaussian Processes are used to model the training performance of tasks. Panel (b) shows how marginal generalization performance is calculated using upper confidence bounds, generalization gap, and generalization performance. Panel (c) shows how the next training task is selected by maximizing the acquisition function. Panel (d) shows how the generalization performance is calculated after training a new policy using zero-shot transfer.
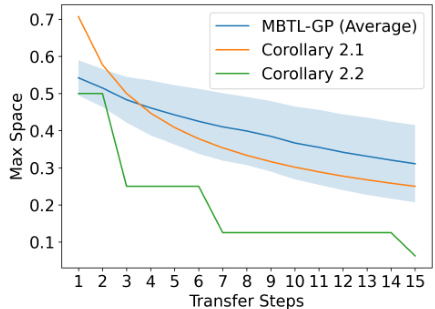
This figure empirically validates the theoretical analysis of regret bounds by comparing the actual reduction in search space achieved by MBTL with the theoretical bounds given by Corollaries 2.1 and 2.2. The x-axis represents the number of transfer steps, and the y-axis represents the size of the maximum search space. The shaded area around the MBTL-GP (Average) line indicates the variability in search space reduction across different runs. The graph shows that MBTL effectively reduces the search space over transfer steps, outperforming the theoretical bounds, which indicates higher sample efficiency.

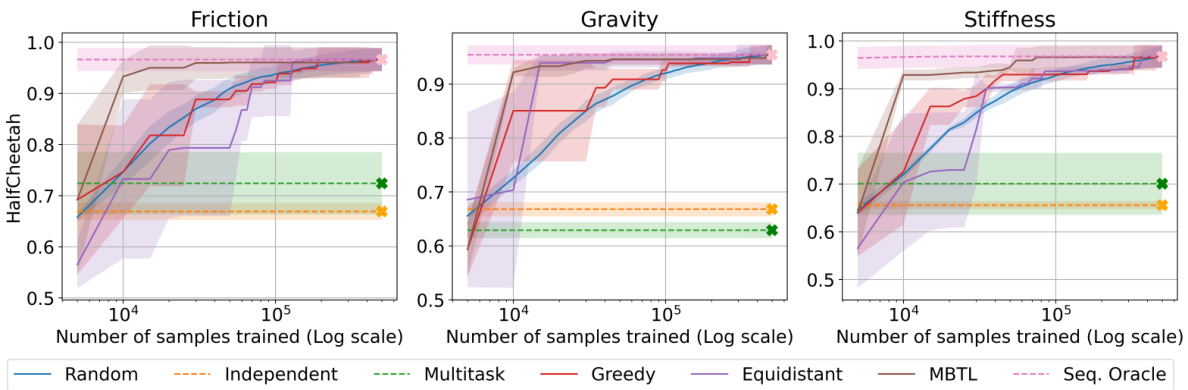
This figure compares the performance of different methods for solving contextual reinforcement learning problems on traffic control tasks. It shows how the normalized performance of each method increases with the number of training samples used. MBTL is shown to significantly outperform independent and multitask learning baselines, achieving comparable performance with drastically fewer training samples (up to 25 times fewer samples). The black dotted line highlights the point at which MBTL surpasses the baselines.
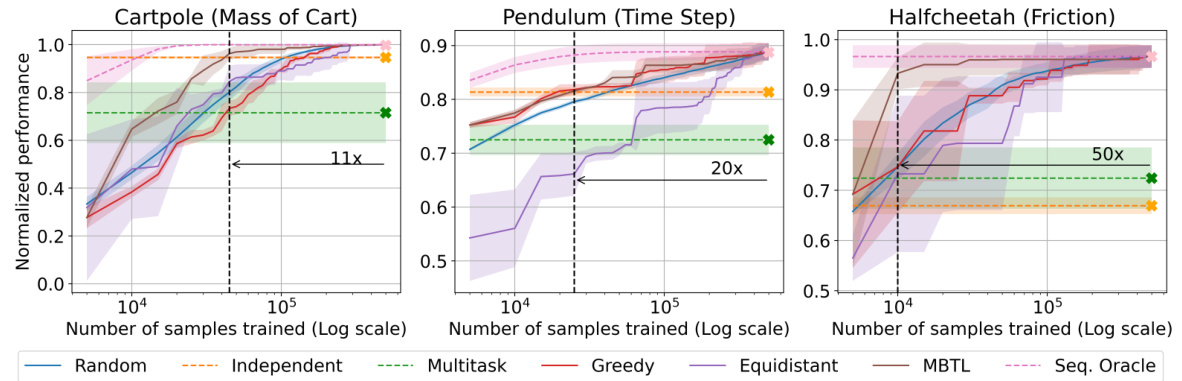
This figure compares the performance of different methods for solving contextual reinforcement learning problems in traffic signal control, eco-driving, and advisory autonomy. The x-axis represents the number of samples trained (log scale), and the y-axis shows the normalized generalized performance. The figure demonstrates that the Model-Based Transfer Learning (MBTL) method significantly outperforms the baselines (Independent, Multi-task, Random, Equidistant, Greedy) by requiring substantially fewer training samples to achieve comparable performance. The black dotted line highlights the point at which MBTL surpasses the baselines, illustrating the significant sample efficiency gains achieved.

This figure shows how the Model-Based Transfer Learning (MBTL) algorithm works step by step. In step 1, the Gaussian Process (GP) makes initial prediction of the performance function. Then, the acquisition function (red line) based on GP prediction and generalization gap is computed to find the next training task. In step 2 and 3, the GP updates the prediction using the new observed performance, then the next training task is selected using the acquisition function. The process repeats until the algorithm reaches the termination condition.
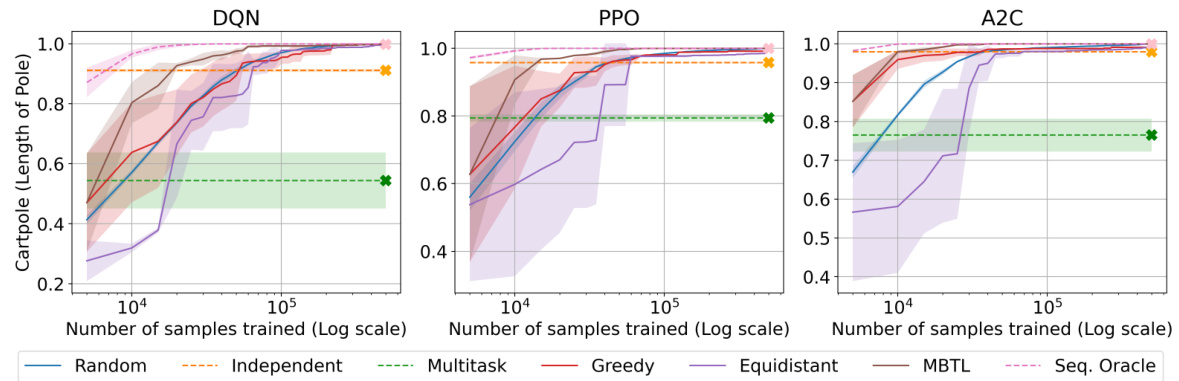
This figure displays the results of a sensitivity analysis performed to evaluate the impact of different deep reinforcement learning (DRL) algorithms on the performance of the Model-Based Transfer Learning (MBTL) method. Three different DRL algorithms were tested: Deep Q-Network (DQN), Proximal Policy Optimization (PPO), and Advantage Actor-Critic (A2C). The results demonstrate that MBTL maintains its effectiveness across these varying algorithms. The x-axis represents the number of samples trained (log scale), while the y-axis represents the normalized performance. The shaded areas indicate the variability in performance across multiple runs.
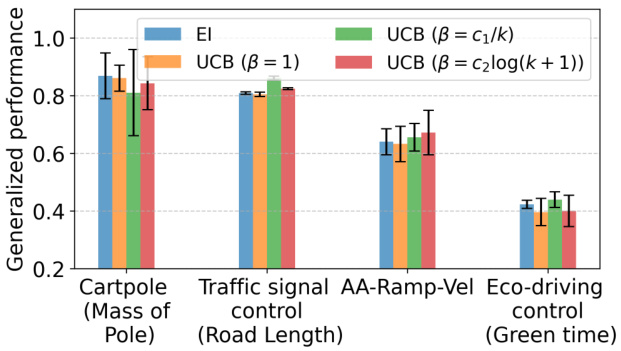
This figure shows the sensitivity analysis performed on different acquisition functions used in the Bayesian optimization within the Model-based Transfer Learning (MBTL) framework. The acquisition functions compared are Expected Improvement (EI), Upper Confidence Bound (UCB) with three different beta parameter settings (β = 1, β = c₁/k, β = c₂log(k + 1)). The generalized performance is evaluated across four different tasks: Cartpole (Mass of Pole), Traffic signal control (Road Length), AA-Ramp-Vel, and Eco-driving control (Green time). Error bars are included to represent the uncertainty in the results. This analysis helps understand the impact of different acquisition functions on the overall performance of MBTL and how sensitive MBTL’s performance is to the specific choice of acquisition function.

The figure illustrates the difference between the actual and predicted performance after a model is trained on a source task (x₁) and used to predict the performance on a different target task (x’). The solid curve represents the actual performance J(πx₁, x’) when the model trained on the source task (x₁) is applied to various target tasks (x’). The dashed curve represents the predicted performance Ĵ(πx₁, x’) based on a model, like Gaussian Process (GP), that estimates the performance. The difference between the curves highlights the generalization gap, which is a key concept in the paper.
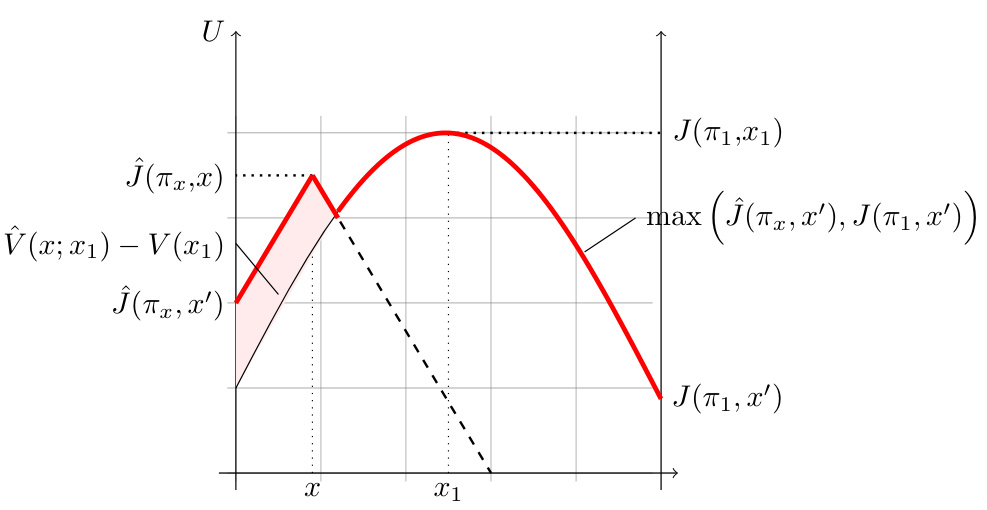
This figure illustrates the process of selecting the next source task (x2) to maximize the estimated marginal improvement in generalization performance. The red curve represents the estimated generalization performance after training on the first selected task (x1), shown as a shaded area under the curve. The difference between the red area (V(x;π1)) and the area under J(π1,x’) (representing the generalization performance achieved so far), represents the marginal improvement. The algorithm aims to select x2 that maximizes this difference.

This figure illustrates the Model-Based Transfer Learning (MBTL) algorithm. It shows how MBTL uses Gaussian processes to estimate training performance, models the generalization gap, and uses Bayesian optimization to select the next training task to maximize generalization performance. The figure is broken down into four parts: (a) shows the Gaussian process regression for estimating training performance; (b) shows how marginal generalization performance is calculated; (c) shows the acquisition function used to select the next task; and (d) shows the zero-shot transfer used to evaluate generalization performance after a task is trained.
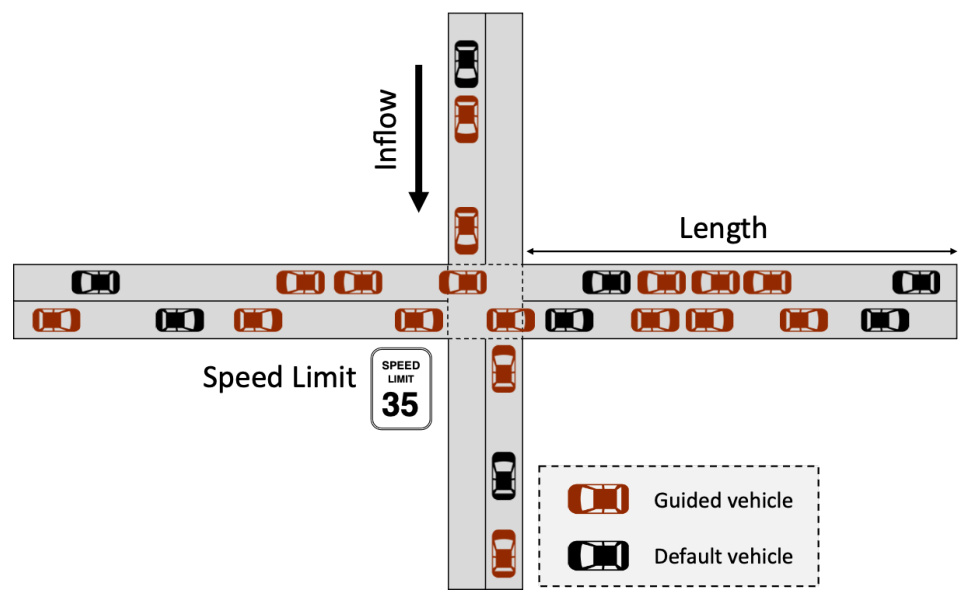
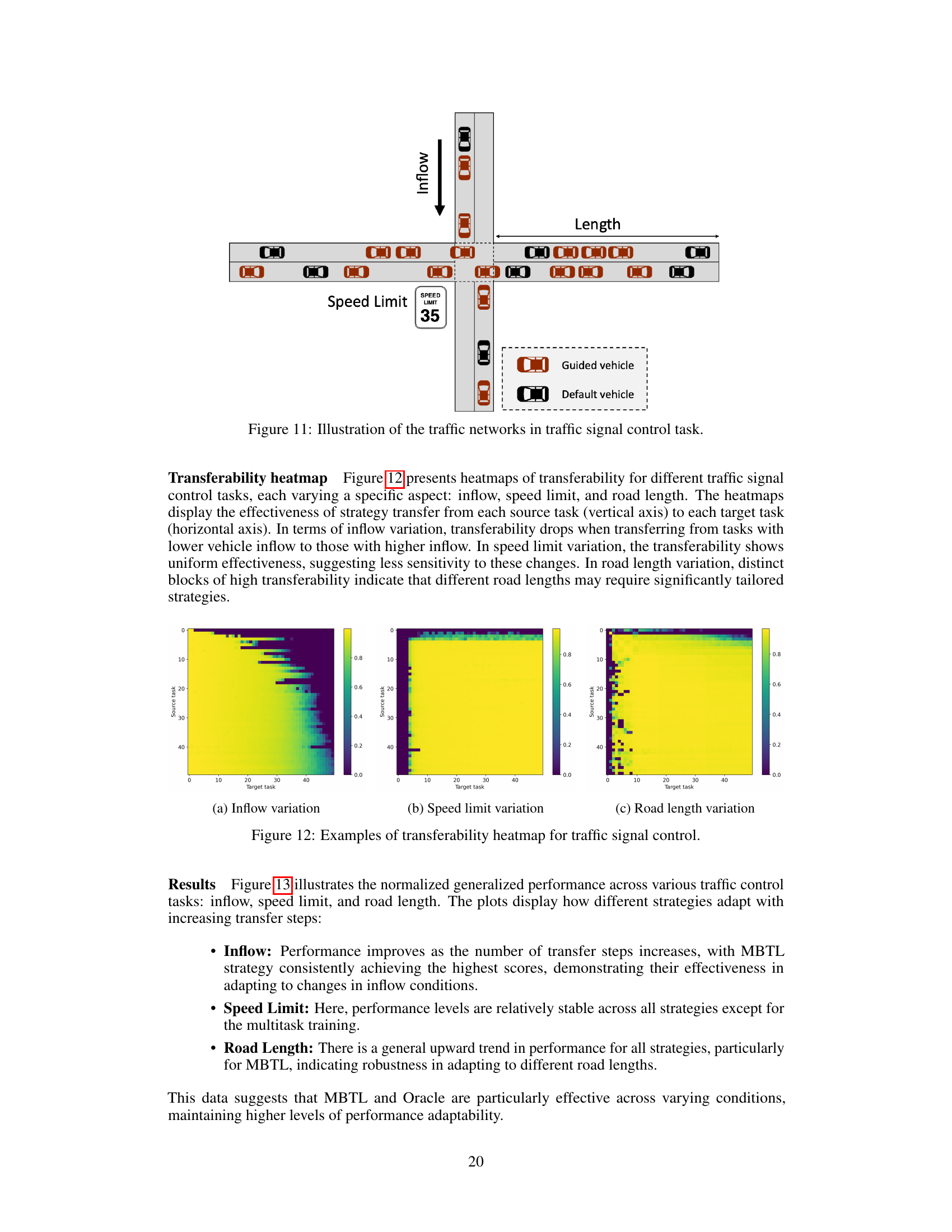
The figure shows a schematic of a four-way intersection controlled by a traffic signal. Vehicles (represented as brown rectangles) approach the intersection from four directions. The inflow of vehicles is indicated by an arrow, and a speed limit sign is shown. The figure also includes a legend distinguishing between guided vehicles (darker brown) and default vehicles (lighter brown). This setup is used to model and study the traffic signal control task in the paper.
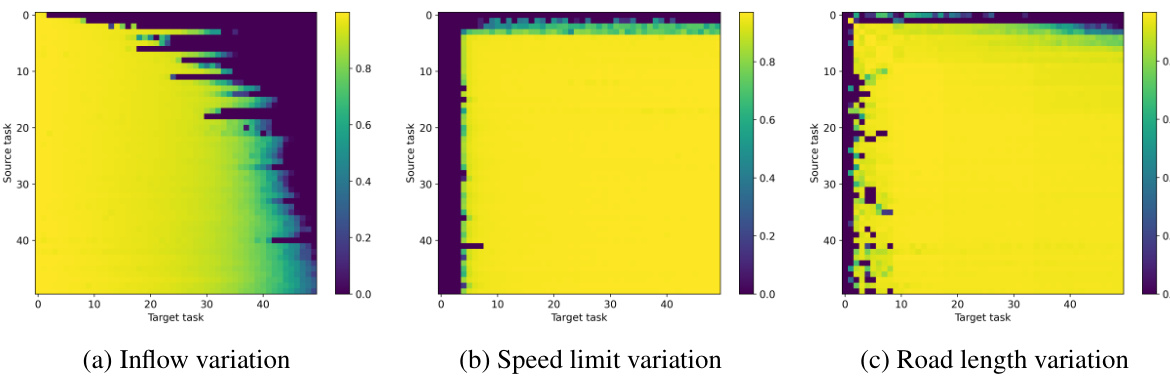
This figure shows three heatmaps visualizing the transferability of strategies for traffic signal control tasks under different variations: inflow, speed limit, and road length. Each heatmap represents the zero-shot transfer performance from each source task (vertical axis) to each target task (horizontal axis), providing insights into how variations in these parameters affect the effectiveness of learned strategies. The heatmaps illustrate how effectively strategies trained on one task generalize to other tasks with varying conditions.
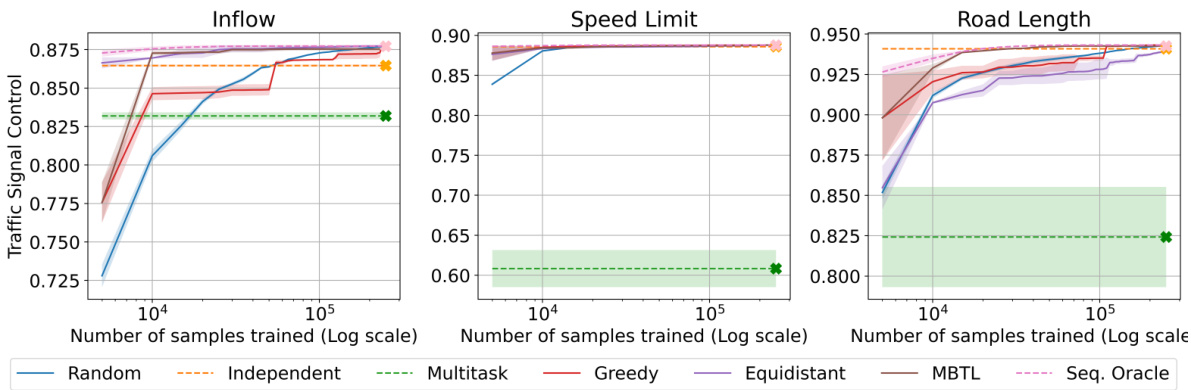
This figure shows the comparison of normalized performance across different methods for traffic CMDP tasks. It highlights the superior sample efficiency of Model-Based Transfer Learning (MBTL) compared to other baselines (Independent, Multi-task, Random, Equidistant, Greedy, Sequential Oracle). The black dotted line indicates when MBTL surpasses the Independent and Multi-task methods, showcasing an improvement of sample efficiency by up to 25 times.
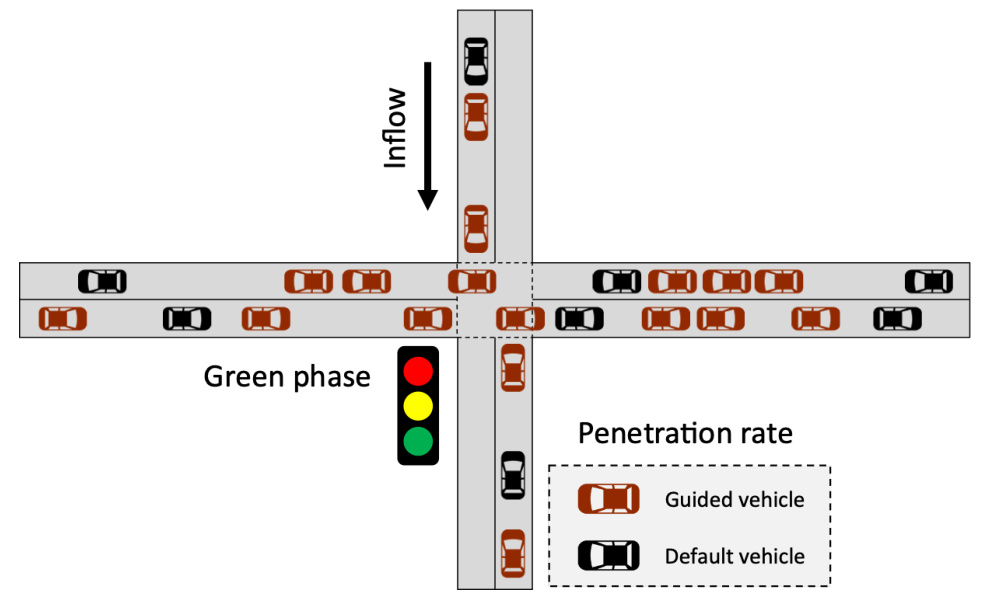
This figure shows a simplified representation of a four-way intersection with vehicles approaching from four directions. The vehicles are represented by brown rectangles, with some labeled as ‘Guided vehicle’ and others as ‘Default vehicle.’ This distinction likely represents a scenario where some vehicles are part of an eco-driving system and others are not. A traffic signal is present, with a green and yellow light indicating the current phase. The diagram illustrates the state variables such as the positions and velocities of all vehicles, and the context variables like the current traffic light status, inflow of vehicles, and the penetration rate of guided vehicles (the proportion of eco-driving vehicles within the system).

The figure displays three heatmaps illustrating the transferability of strategies learned for eco-driving control tasks under different conditions. Each heatmap shows transferability from various source tasks (vertical axis) to different target tasks (horizontal axis) for a specific contextual variation. (a) shows heatmap for green phase variation, (b) for inflow variation, and (c) for penetration rate variation. The color intensity represents the level of transferability, with brighter colors indicating higher transferability.
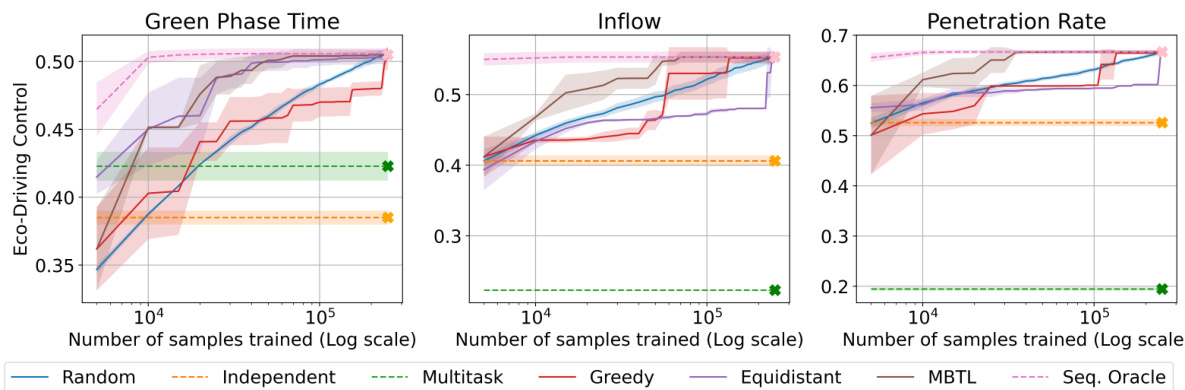
This figure compares the performance of different methods (Random, Independent, Multitask, Greedy, Equidistant, MBTL, and Sequential Oracle) on traffic CMDP tasks. The x-axis represents the number of samples trained (log scale), while the y-axis shows the normalized generalized performance across all tasks. The figure showcases that MBTL quickly surpasses the performance of Independent and Multitask training methods, demonstrating a significant improvement in sample efficiency (up to 25x fewer samples). The black dotted line visually emphasizes this significant performance jump achieved by MBTL.
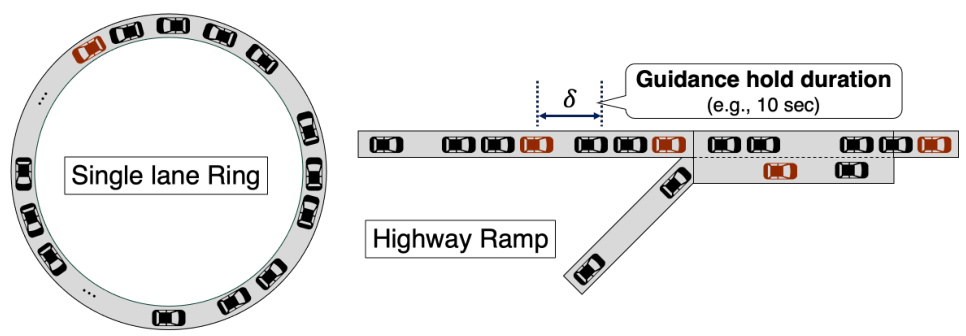
The figure shows two different traffic network configurations used in the advisory autonomy task: a single-lane ring and a highway ramp. The single-lane ring is a simplified scenario where vehicles circulate in a single lane, suitable for testing basic guidance strategies. The highway ramp introduces a more complex and realistic scenario involving merging traffic from an on-ramp onto the main highway, which presents significant challenges for vehicle guidance systems, particularly concerning stop-and-go traffic and the coordination of multiple vehicles. The ‘guidance hold duration (e.g., 10 sec)’ indicates that the guidance provided to the driver is not continuous but rather happens periodically at a given time interval, making the task more challenging in the context of human driver behavior.

This figure visualizes the transferability of strategies learned from source tasks to target tasks in traffic signal control under three types of context variations: inflow, speed limit, and road length. Each heatmap shows the effectiveness of transferring strategies from each source task (vertical axis) to each target task (horizontal axis). The color intensity represents the transferability score; warmer colors indicate higher transferability scores and vice versa. The heatmaps reveal patterns and insights into which source tasks are most effective for generalization to specific target tasks based on the type of context variation. This helps understand the sensitivity of different traffic signal control strategies to changes in the environment and informs the design of more robust and adaptable traffic control systems.
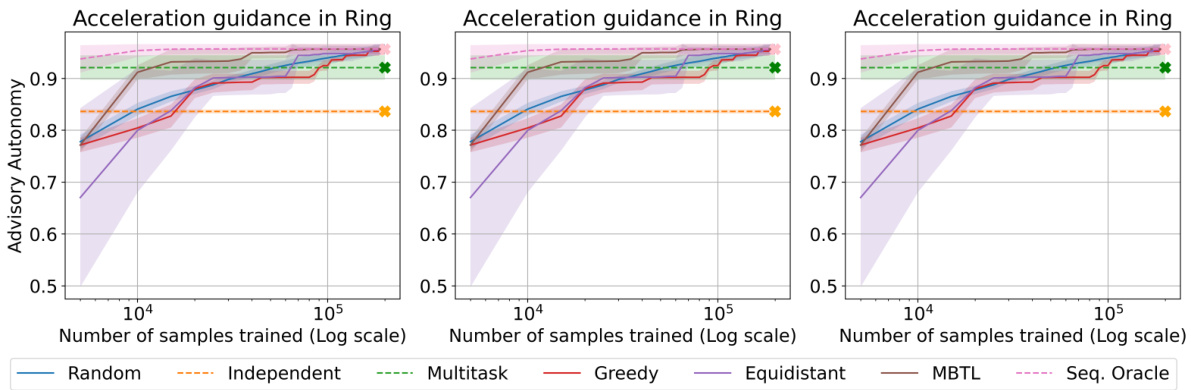
This figure presents a comparison of the normalized generalized performance across different strategies for the advisory autonomy task. Three sub-figures show the results for three different runs, indicating the consistency of the results. Each sub-figure shows how the performance of different methods (Random, Independent, Multitask, Greedy, Equidistant, MBTL, Sequential Oracle) changes with the number of samples trained (log scale). The performance metric is advisory autonomy, and the x-axis represents the number of samples used for training, shown on a logarithmic scale. The lines and shaded areas represent the average performance and confidence intervals across multiple trials for each method. The star symbol (*) indicates the best average performance achieved. The results show that MBTL consistently outperforms the other methods, demonstrating its robust adaptability to changing task parameters.

This figure shows three heatmaps visualizing the transferability of strategies in the Cartpole task. Each heatmap represents a different contextual variation: (a) mass of the cart, (b) length of the pole, and (c) mass of the pole. The heatmaps’ x and y axes represent the source and target tasks respectively, with color intensity representing the transferability. Brighter colors denote higher transferability, meaning that a policy trained on a source task performs well when applied to a similar target task. The heatmaps illustrate how contextual similarity influences transferability, which is a key concept explored in the Model-Based Transfer Learning (MBTL) framework discussed in the paper.

This figure compares the performance of different methods (Random, Independent, Multitask, Greedy, Equidistant, MBTL, and Sequential Oracle) across three variations of the Cartpole task: varying mass of the cart, length of the pole, and mass of the pole. The x-axis represents the number of training samples (log scale), and the y-axis represents the normalized generalized performance. The shaded area around each line indicates the standard deviation across multiple runs. The figure demonstrates the sample efficiency of MBTL, especially when compared to Independent and Multitask training. MBTL shows close-to-oracle performance, highlighting its effectiveness in this control domain.
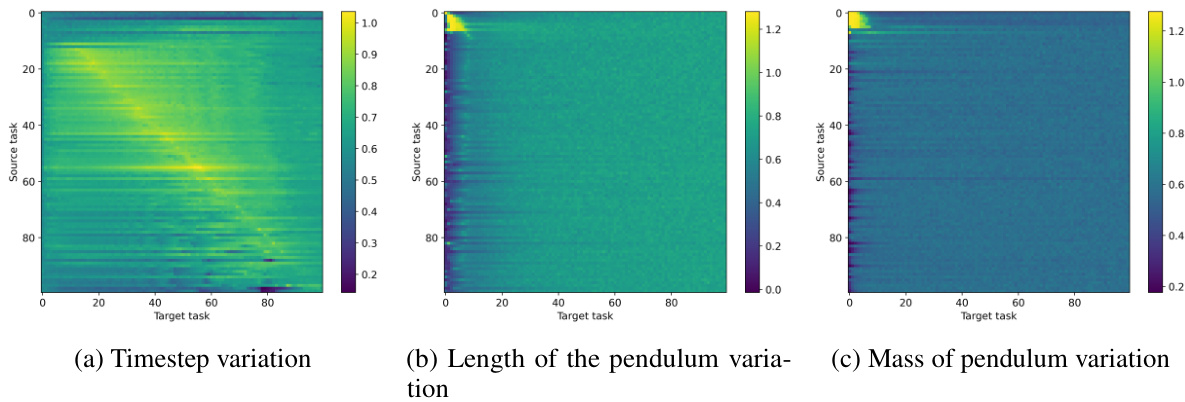
This figure shows three heatmaps visualizing the transferability of strategies for the Pendulum task across variations in three physical properties: timestep, length of the pendulum, and mass of the pendulum. Each heatmap displays the effectiveness of strategy transfer from source tasks (vertical axis) to target tasks (horizontal axis). The heatmaps illustrate how effectively strategies trained on one set of parameters generalize to other sets. High transferability (yellow/green) indicates good generalization across different parameter settings. Low transferability (blue/purple) suggests that strategies trained for one setting may not perform well under different conditions. The patterns in each heatmap reveal how the pendulum’s dynamic behavior changes as a function of timestep, length, and mass.

This figure displays the comparison of normalized generalized performance across various strategies for the Pendulum task. The three subplots show results for variations in timestep, length of the pendulum, and mass of the pendulum. The results show that MBTL strategies consistently achieve high scores, demonstrating adaptability to changes in pendulum dynamics.

The figure shows three heatmaps visualizing the transferability of strategies in the BipedalWalker task, each with variations in friction, gravity, and scale. The color intensity in each heatmap represents the success of transferring a policy trained on a source task (vertical axis) to a target task (horizontal axis) with specific parameter variations. Darker colors indicate lower transferability. The heatmaps offer insights into the impact of these physical properties on the generalizability of learned control strategies.

This figure shows the results of the BipedalWalker experiment, comparing the performance of different algorithms across variations in three physical properties: friction, gravity, and scale. Each plot shows the learning curves for various algorithms, including random selection, independent training, multitask learning, a greedy strategy, an equidistant strategy, MBTL, and a sequential oracle. The shaded regions represent confidence intervals. The green dashed line indicates the performance of the best baseline algorithm. The results illustrate that MBTL consistently achieves performance comparable to or exceeding the best baseline methods, often with significantly fewer samples.

The figure shows three heatmaps visualizing the transferability of strategies for the HalfCheetah task across variations in friction, gravity, and stiffness. Each heatmap displays the effectiveness of transferring strategies from source tasks (vertical axis) to target tasks (horizontal axis). The heatmaps illustrate how different physical properties influence strategy adaptability. For instance, the friction variation heatmap reveals uniform high transferability, while gravity and stiffness variations show less consistent transferability, indicating a higher sensitivity to changes in those parameters.
The figure shows a comparison of the normalized generalized performance across various strategies for the HalfCheetah task with respect to varied physical properties (friction, gravity, and stiffness). The results indicate that MBTL generally outperforms other methods, especially when managing variations in gravity and stiffness, showing superior adaptability to physical changes in the task environment. The trends across different parameters confirm the impact of task-specific dynamics on the effectiveness of the tested strategies.
More on tables
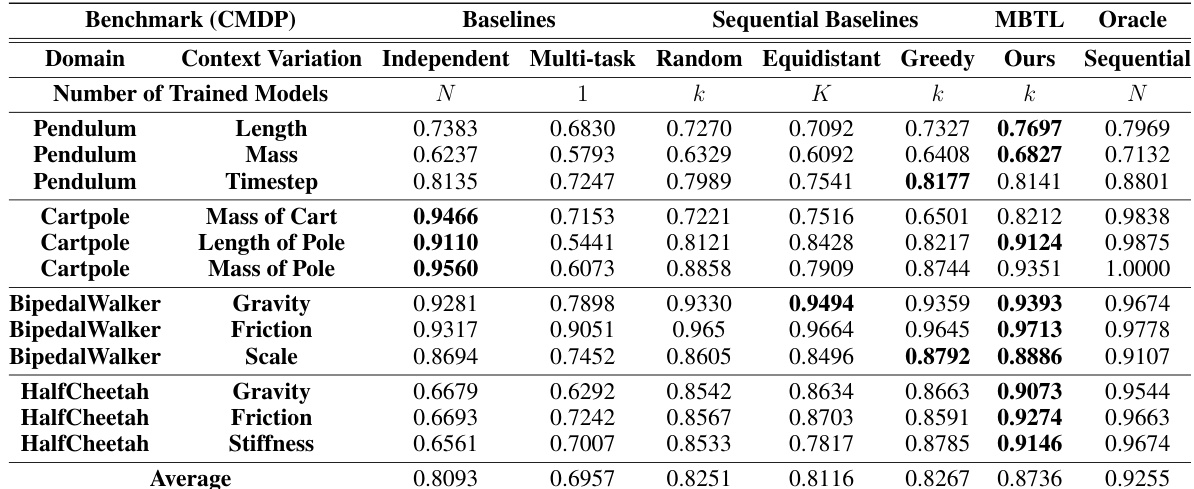
This table compares the performance of various methods for solving contextual Markov Decision Processes (CMDPs) in traffic control domains. It contrasts the performance of several baselines (Independent, Multi-task, Random, Equidistant, Greedy) with the proposed Model-Based Transfer Learning (MBTL) method and an Oracle. The table shows the performance for different traffic control tasks (context variations), providing a quantitative comparison across approaches for evaluating sample efficiency and the ability to generalize across various tasks.

This table presents a comparison of the performance of various methods on traffic CMDPs. It compares the performance of the proposed Model-Based Transfer Learning (MBTL) method against several baselines, including independent training, multi-task training, random selection, equidistant strategy, and a greedy strategy. The table shows the performance of each method across different traffic control domains and context variations, indicating the effectiveness of MBTL in achieving high performance and sample efficiency. Higher values generally indicate better performance.
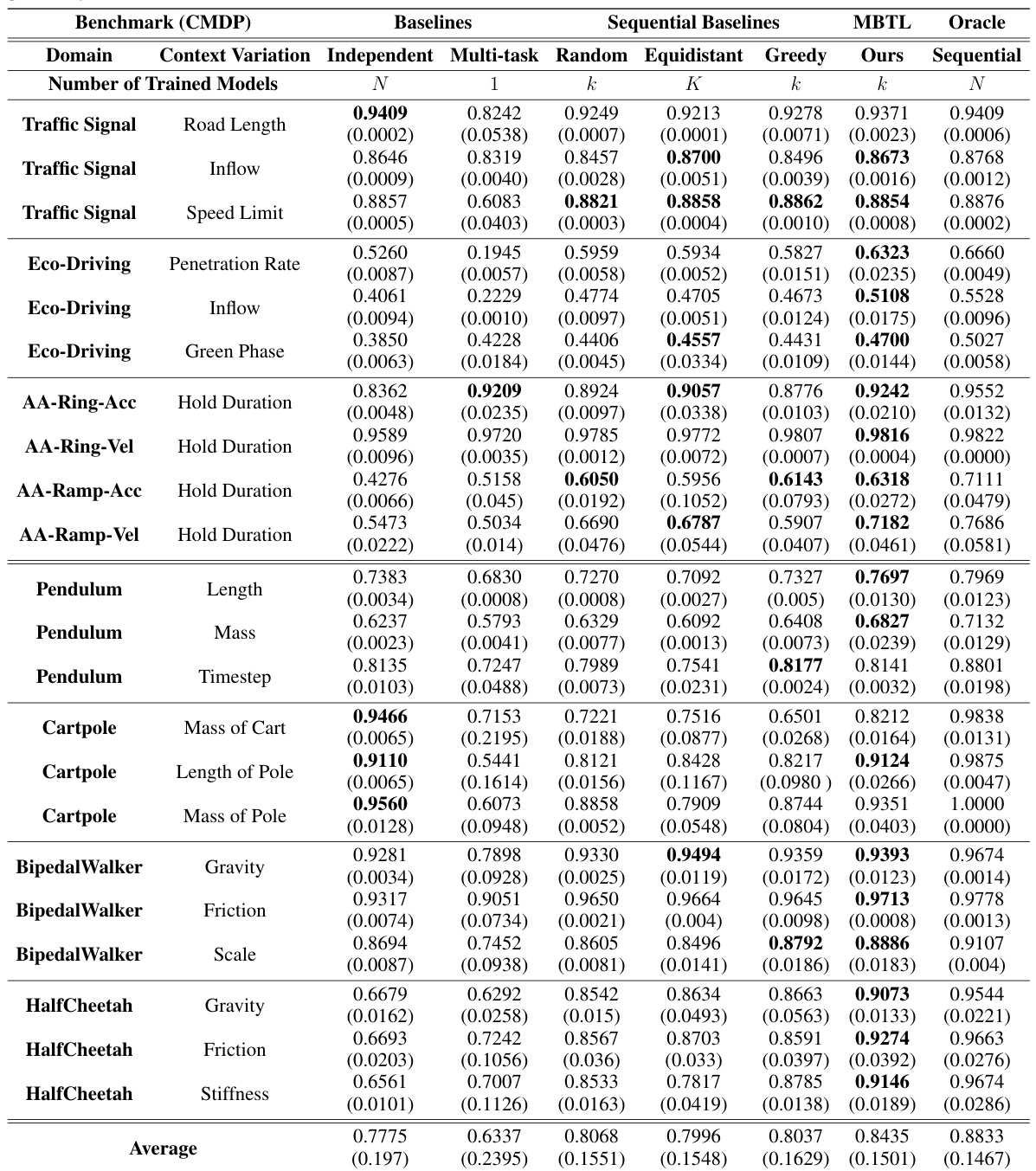
This table presents a comparison of the performance of different methods on various traffic-related Contextual Markov Decision Processes (CMDPs). The methods compared include several baselines (Independent, Multi-task, Random, Equidistant, Greedy) and the proposed method (MBTL), along with an Oracle. Performance is measured across various CMDPs with different context variations (e.g., Inflow, Speed Limit, Penetration Rate). The table shows the average performance for each method, indicating the relative sample efficiency and generalization capability of each approach across different tasks. Higher values generally indicate better performance.
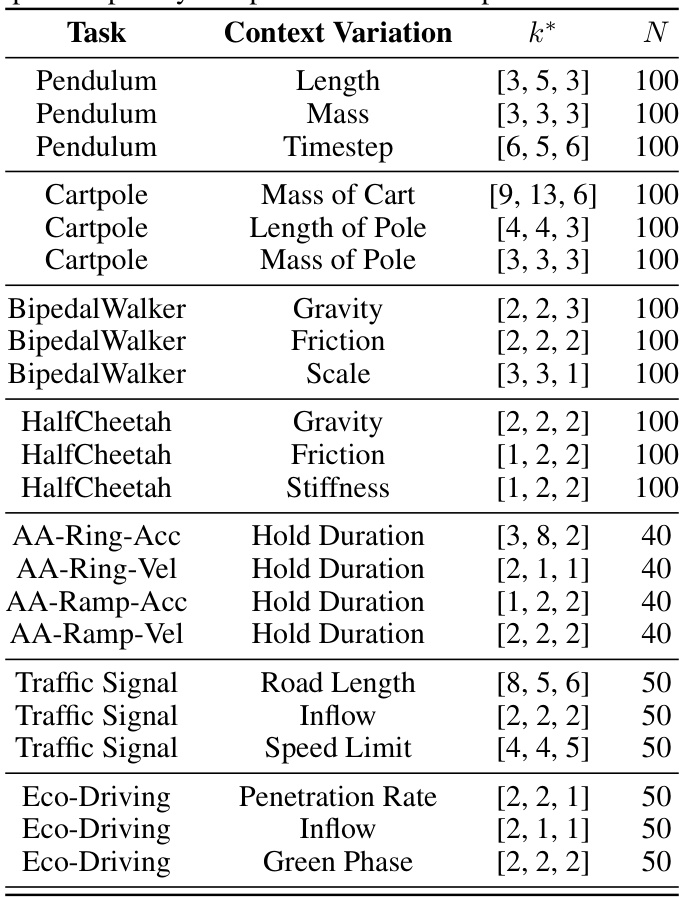
This table presents a comprehensive comparison of various reinforcement learning methods applied to context-variant traffic control and standard continuous control benchmark tasks. It compares the performance of different methods, including Independent, Multi-task, Random, Equidistant, Greedy, Sequential, MBTL (the proposed method), and Oracle (perfect knowledge) across various contexts. The results show sample efficiency improvements, indicating the effectiveness of MBTL in handling contextual variations.
Full paper#