TL;DR#
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on online matching and fair division problems. It presents a novel algorithmic solution that achieves simultaneous fairness and efficiency in a previously unsolved problem, opening up new avenues for research in online resource allocation and shedding light on the inherent trade-offs between fairness and optimality. The paper also provides tight upper bounds, improving our theoretical understanding of the limitations in achieving fairness. This work’s impact extends to various applications involving resource allocation such as advertisement slot allocation, ride-sharing, and food bank distribution. The introduction of the “price of fairness” offers a new framework to study the fundamental trade-offs in fair resource allocation.
Visual Insights#
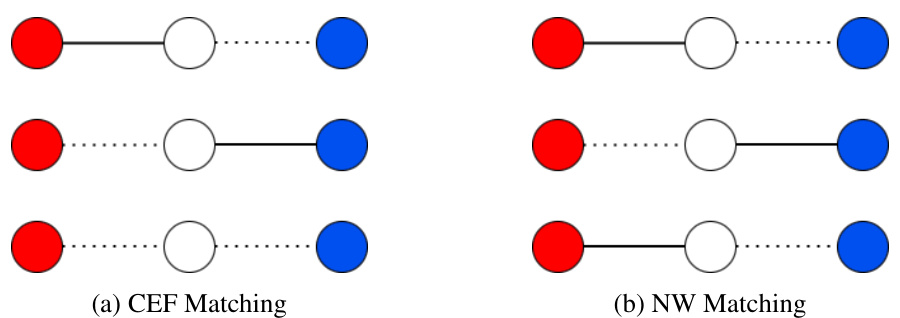
🔼 The figure shows two examples of matchings between two classes of agents (red and blue) and items (white). The left-hand side shows a class envy-free (CEF) matching, where no class of agents would prefer the items assigned to another class. The right-hand side depicts a non-wasteful (NW) matching, demonstrating a scenario where items are not allocated to agents who like them, even though it is possible to improve the matching size. The figure illustrates the trade-off between fairness and efficiency in matching problems.
read the caption
Figure 1: Examples of class envy-free (CEF) and non-wasteful (NW) matchings where bolded lines indicate a matching. Red nodes indicate agents in the first class, blue nodes indicate agents in the second class, and white nodes indicate items.

🔼 This table summarizes the performance of randomized algorithms for online class matching, comparing the achieved approximation ratios for USW, CEF, and CPROP objectives against theoretical upper bounds. It shows that the proposed algorithm provides simultaneous guarantees for all three objectives, while the upper bounds apply individually to each objective. Results from existing literature for divisible settings are also included for comparison.
read the caption
Table 1: The summary of our results on randomized algorithms. Each algorithm achieves its three guarantees simultaneously, while the upper bound holds for any algorithm, separately for each guarantee. Results from prior works in the divisible setting are noted with citation for completeness.
In-depth insights#
Online Fairness#
Online fairness, in the context of resource allocation, presents unique challenges. Unlike traditional fairness problems, where all resources and agents are known upfront, online settings involve dynamic arrivals of resources and immediate irrevocable decisions. This necessitates algorithms that balance fairness and efficiency in real-time. Key challenges include ensuring equitable distribution across different classes of agents, handling uncertainty about future arrivals, and defining appropriate fairness metrics for online scenarios. Algorithmic approaches must contend with the trade-off between optimal resource allocation (maximizing total welfare) and achieving fairness. Research in this field explores randomized algorithms and approximation guarantees, aiming for algorithms that maintain fairness while staying computationally efficient. The price of fairness, the trade-off between optimal and fair allocations, is a crucial consideration. This involves evaluating how much loss in total utility is acceptable to achieve a certain level of fairness. The study of online fairness requires careful analysis of various fairness metrics, handling different types of resources (divisible or indivisible), and addressing the complexities of real-world applications.
Class Envy-Freeness#
Class envy-freeness (CEF) is a fairness concept crucial in resource allocation, especially when dealing with multiple groups or classes of agents. It ensures that no class feels unfairly treated by comparing its allocation to the best possible allocation any other class could have received. The challenge lies in defining and measuring this ‘best possible’ allocation, particularly when resources are indivisible. Different notions of CEF exist, such as a-CEF which offers an approximation guarantee, and CEF1, which permits minor envy. Achieving CEF, especially in online settings where resources arrive sequentially and decisions are irreversible, is computationally complex and may not always be feasible. The paper explores the tradeoffs between CEF and other desirable properties like efficiency (utilitarian social welfare) and non-wastefulness, highlighting the inherent tension between fairness and optimality.
Algorithmic Guarantees#
The core of the research lies in establishing algorithmic guarantees for online class fair matching. The authors aim to design algorithms that provide approximations to various fairness objectives (class envy-freeness, class proportionality) while simultaneously ensuring efficiency (non-wastefulness). A key challenge addressed is the inherent trade-off between fairness and efficiency, particularly when dealing with indivisible items. The analysis involves demonstrating both achievable approximation ratios through novel randomized algorithms and proving upper bounds on what is possible to achieve with any algorithm (both randomized and deterministic). The results highlight the limitations of deterministic approaches and emphasize the role of randomization in achieving reasonable fairness guarantees in online settings. The study provides a framework for evaluating trade-offs between optimal and fair matching through a newly defined concept of the ‘price of fairness’, further enriching our understanding of these complex algorithmic challenges.
Price of Fairness#
The concept of “Price of Fairness” in the context of online class matching explores the trade-off between achieving optimal resource allocation (maximizing utilitarian social welfare or USW) and ensuring fairness among different classes of agents. The inherent tension arises because maximizing USW might lead to inequitable distributions across classes, even if it results in a higher overall number of successful matchings. The analysis delves into the quantification of this trade-off, often by showing how increasing the level of fairness (e.g., measured by the degree of approximation to class envy-freeness or CEF) directly impacts the achievable USW. A key finding in this research area would likely reveal an inverse proportionality relationship: higher levels of fairness in the final matching come at a cost of lower overall efficiency, and vice versa. This necessitates careful consideration of fairness constraints when designing algorithms for online resource allocation. The “Price of Fairness” highlights the need for a nuanced approach that considers both efficiency and fairness objectives, potentially through the development of novel algorithms that achieve a suitable balance between these competing goals. This is often explored via theoretical frameworks, but also through practical examples in areas like online marketplaces or resource allocation.
Future Directions#
Future research could explore extending the online class fair matching problem to incorporate more realistic settings such as dynamically changing class structures or agent preferences that evolve over time. Investigating the impact of imperfect information about agent preferences or class characteristics is crucial. The development of more sophisticated algorithms, potentially leveraging machine learning techniques, to approximate fairness guarantees more closely is another key area. Finally, a deeper examination into the trade-offs between various fairness criteria in dynamic resource allocation settings is needed to guide practical algorithm design, possibly through improved theoretical bounds. Ultimately, the goal is robust and efficient algorithms applicable to real-world scenarios, offering both fairness and efficiency.
More visual insights#
More on figures

🔼 This figure presents two impossibility constructions used to prove upper bounds on the achievable class envy-freeness (CEF) approximation for online class matching problems. (a) shows a construction demonstrating a tight bound of approximately 0.761 for the indivisible item setting; (b) shows a construction proving a tighter bound of approximately 0.677 for the divisible item setting. These constructions demonstrate that no algorithm can achieve better CEF approximations while maintaining non-wastefulness.
read the caption
Figure 2: Impossibility constructions for the upper bound results of Theorems 1.2 and 1.3. (a) the indivisible setting construction for an at most (2-1)-CEF approximation, (b) the divisible setting construction for an at most 0.677-CEF approximation.
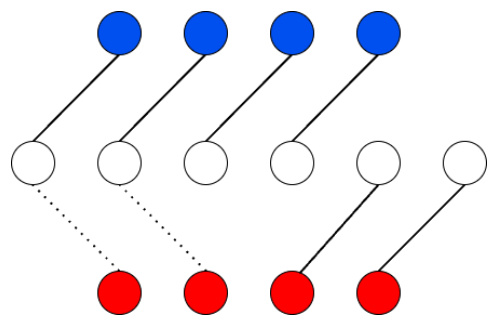
🔼 The figure shows a bipartite graph representing a hardness instance for Theorem A.4, which demonstrates that a non-wasteful CEF matching does not guarantee maximization of class Nash social welfare (CNSW). The graph includes two classes of agents (red and blue nodes), and items (white nodes). The connections show which agents like which items. The structure of the graph and the connection is designed to show that even if a matching is class envy-free (CEF) and non-wasteful, it does not necessarily maximize the CNSW objective function.
read the caption
Figure 3: Hardness instance for Theorem A.4.
Full paper#



















