↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Transformer networks are powerful but computationally expensive, especially when scaled up for better performance. This results in limitations of deployment and training, hindering accessibility for many researchers. There’s also a diminishing return in performance by just increasing the number of layers. The need to address these limitations and improve model efficiency is crucial.
DenseFormer addresses these issues by using depth-weighted averaging (DWA) after each transformer block, integrating information from past representations. This simple modification significantly enhances data efficiency, enabling the model to reach the same perplexity as much deeper models but requiring less memory and time. Extensive experiments demonstrate DenseFormer’s superior speed and performance, paving the way for more efficient and scalable transformer models. The key is the DWA module, which efficiently leverages past representations to speed up training and inference while improving performance.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces DenseFormer, a novel architecture that significantly improves the efficiency and performance of transformer models. This offers a potential solution to the limitations of scaling transformers, a crucial challenge in NLP and other fields, making it highly relevant to current research trends and opening new avenues for investigation in model optimization and efficiency.
Visual Insights#

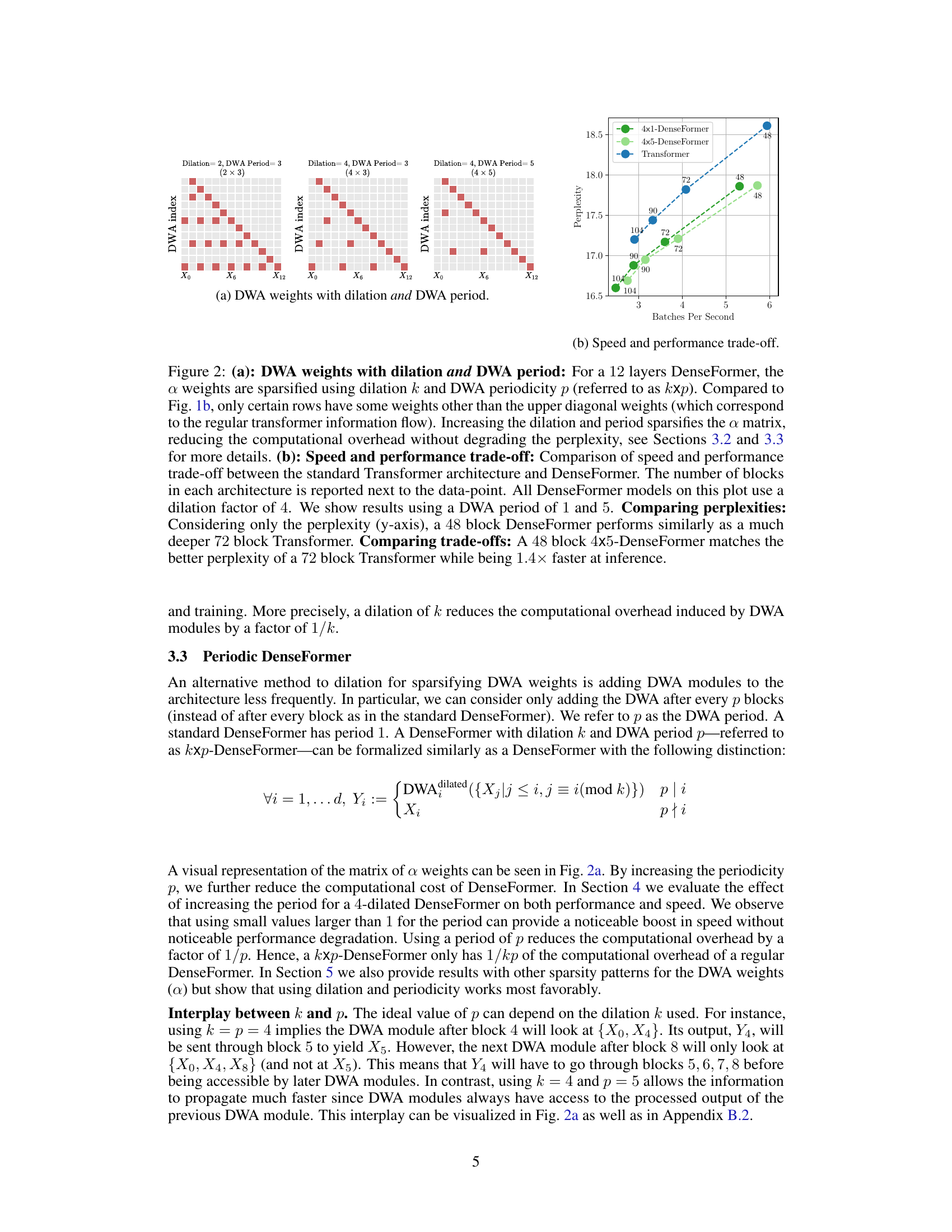
This figure illustrates the DenseFormer architecture. Part (a) shows a simplified representation with two transformer blocks and how the Depth Weighted Average (DWA) module combines outputs from current and previous blocks. Part (b) displays the DWA weights in matrix form for a 12-layer DenseFormer, demonstrating how the weights are learned and the effect of dilation on sparsity.
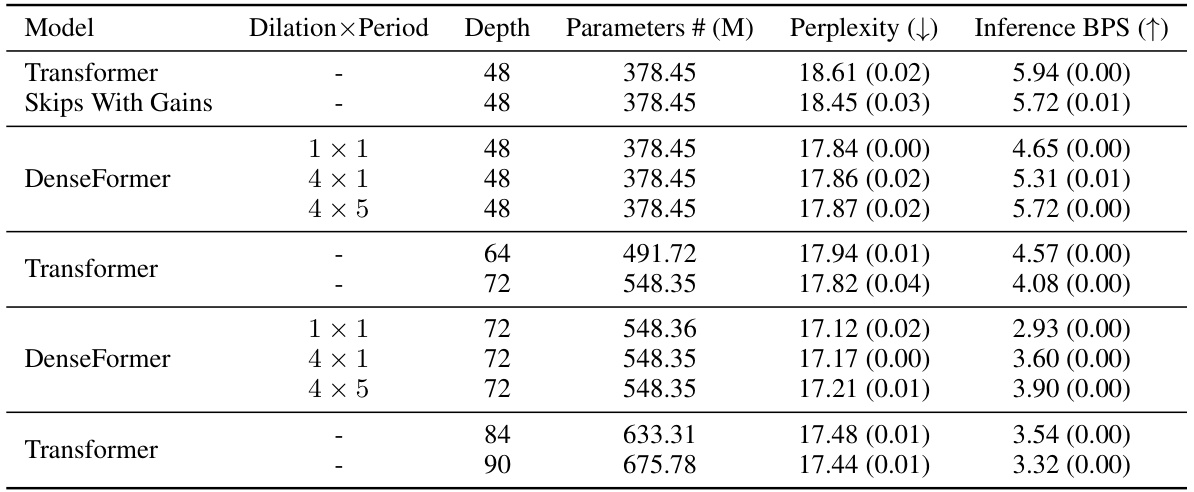
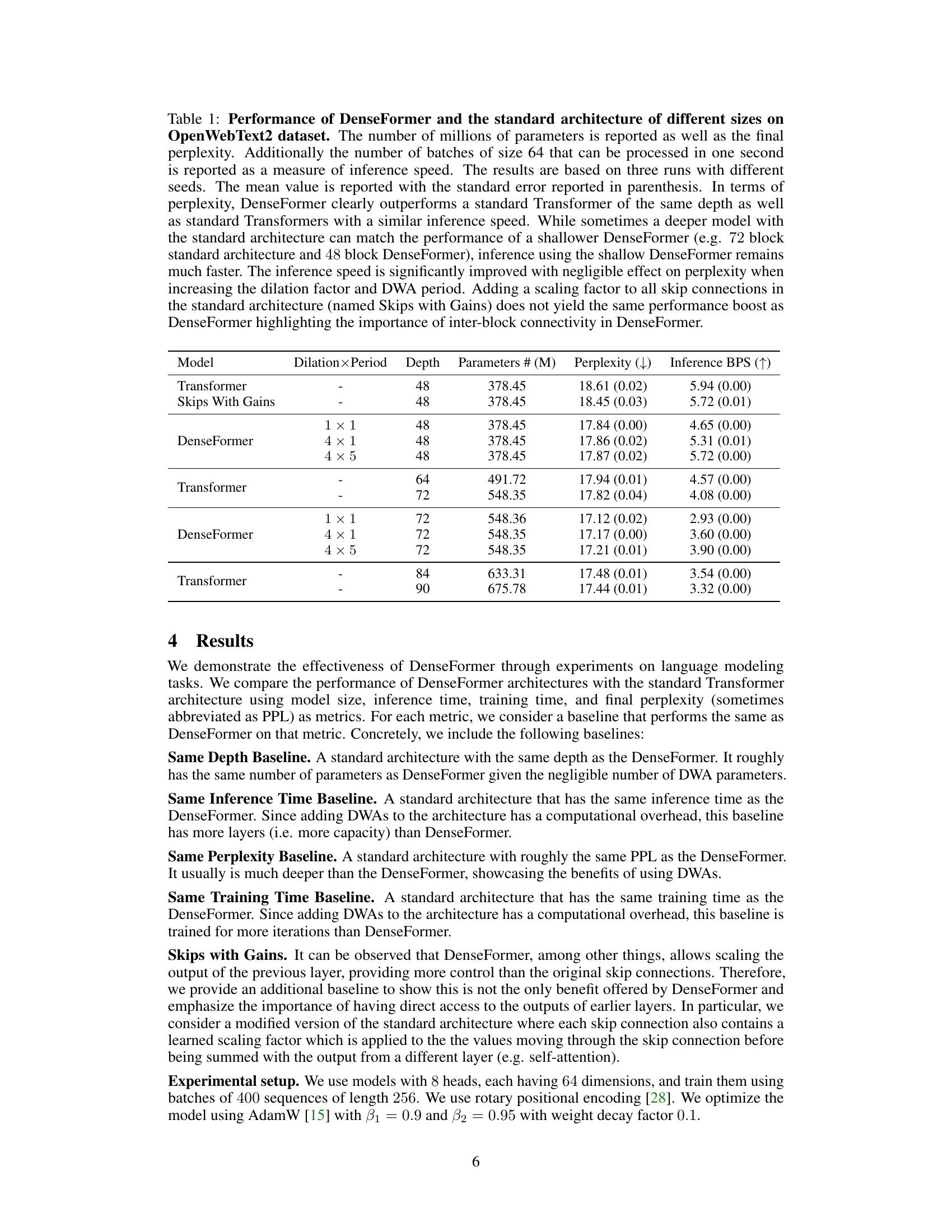
This table compares the performance of DenseFormer and standard Transformer models of various sizes on the OpenWebText2 dataset. It shows the number of parameters, perplexity, and inference speed (in batches per second) for each model. Results demonstrate that DenseFormer consistently outperforms standard Transformers of the same depth and achieves comparable or better perplexity at significantly faster inference speeds, showcasing its superior efficiency.
In-depth insights#
DenseFormer Intro#
The introduction to DenseFormer highlights the limitations of scaling the Transformer architecture. Larger models, while improving performance, come with significantly increased computational costs and memory requirements, making them inaccessible to many researchers and institutions. The paper posits that simply increasing model size or depth eventually reaches diminishing returns. DenseFormer is presented as a simple yet effective modification to the standard Transformer architecture that addresses these limitations. By incorporating a depth-weighted averaging (DWA) mechanism after each Transformer block, DenseFormer aims to improve information flow and data efficiency. This approach allows for the reuse of activations from earlier layers, potentially leading to better performance with fewer parameters and faster inference. The introduction effectively sets the stage by establishing the problem and proposing DenseFormer as a novel solution that offers a compelling speed-performance trade-off.
Depth-Weighted Avg#
The concept of ‘Depth-Weighted Averaging’ presents a novel approach to enhance information flow within transformer networks. Instead of relying solely on skip connections, Depth-Weighted Averaging (DWA) computes a weighted average of intermediate representations from all preceding layers, including the initial input embedding, before feeding the result to the next transformer block. This mechanism allows deeper layers to directly access and utilize information from earlier layers, potentially mitigating the vanishing gradient problem and improving data efficiency. The weights themselves are learned parameters, and their structure reveals coherent patterns in information flow, suggesting a structured and learned reuse of activations from across the network’s depth. This method demonstrates improvements in perplexity while simultaneously offering potential gains in memory efficiency and inference speed, especially when coupled with architectural modifications like dilation and periodicity that sparsify the DWA computations without significant performance loss. The learned patterns of DWA weights also offer valuable insights into the model’s internal processing and the information flow dynamics within deep transformer architectures.
DWA Sparsity#
DWA sparsity, a crucial aspect of the DenseFormer architecture, focuses on efficiently managing the computational cost associated with depth-weighted averaging (DWA). The core idea is to strategically reduce the number of connections in the DWA module by introducing sparsity patterns. This is achieved through techniques like dilation, which skips connections across layers, and periodicity, which introduces DWA modules only at periodic intervals rather than after every transformer block. These methods drastically reduce the computational overhead of DWA without significantly impacting model performance. The learned DWA weights themselves exhibit coherent patterns, revealing structured information flow and supporting the effectiveness of sparsity. Finding the optimal balance between sparsity level and performance is key, as excessive sparsity can lead to performance degradation. The investigation into different sparsity patterns highlights the importance of preserving key inter-block connections for optimal performance. The use of dilation and periodicity is found to be particularly effective, striking a balance between performance and reduced computational load.
Resource Impact#
The resource impact of the DenseFormer architecture is a key consideration. While adding depth-weighted averaging (DWA) modules introduces additional parameters, the authors demonstrate this overhead is negligible for large-scale models, adding only a few thousand parameters at most. Memory efficiency is also enhanced because DWA modules don’t require additional memory beyond what is already needed for standard transformers during training and inference. The computational overhead of DWA is addressed effectively through dilation and periodicity hyperparameters, which sparsify the DWA weight matrix, significantly reducing computation time without sacrificing performance. This makes DenseFormer particularly appealing for resource-constrained environments. Experimental results showcase the superior speed-performance trade-off of DenseFormer compared to deeper standard Transformer models, achieving comparable or better perplexity with substantial gains in inference speed and memory efficiency. Therefore, DenseFormer offers a compelling alternative, especially when data efficiency is a primary concern.
Future Work#
The paper’s ‘Future Work’ section suggests several promising avenues of research. Improving the efficiency of DenseFormer’s implementation is a key priority, potentially through exploring more efficient sparsity patterns within the DWA weights. This is crucial for scaling up to larger models and datasets, and the authors hint that structured patterns in the learned weights might guide the design of these new sparsity patterns. Another significant area is enabling efficient distributed training, as this is essential to tackle larger-scale problems. Given the nature of the depth-weighted averaging, efficiently sharding the DWA module across multiple nodes represents a substantial challenge and a major focus for future work. Finally, the authors note the potential for exploring applications beyond language modeling, highlighting the generic nature of DenseFormer and its potential applicability to other domains. This suggests the need for further investigation into how the architecture can be adapted and optimized for diverse tasks and data types.
More visual insights#
More on figures
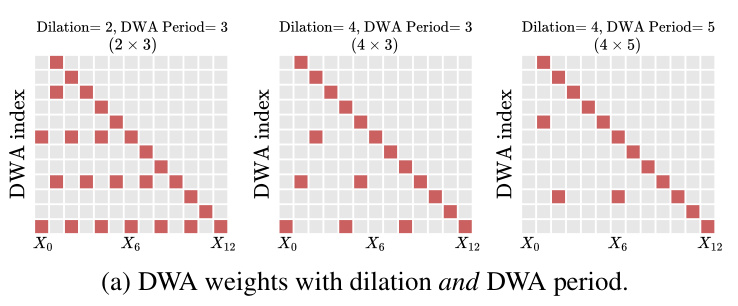
This figure shows the effects of dilation and DWA period on the sparsity of the DWA weights and the resulting speed-performance trade-off between DenseFormer and standard Transformer models. Part (a) visualizes how increasing dilation and period reduces the number of non-zero weights in the DWA matrix. Part (b) illustrates that DenseFormer achieves comparable perplexity to much deeper Transformers while significantly improving inference speed, demonstrating the efficiency gains from the proposed architectural modifications.
This figure shows the effect of dilation and DWA period on the sparsity of the DWA weight matrix and the resulting speed-performance trade-off. Part (a) illustrates how increasing dilation and period reduces the number of non-zero weights, while part (b) demonstrates that DenseFormer achieves comparable or better perplexity than standard Transformers with significantly faster inference speed, especially with dilation and period optimization. The improvements in speed are achieved without sacrificing perplexity.

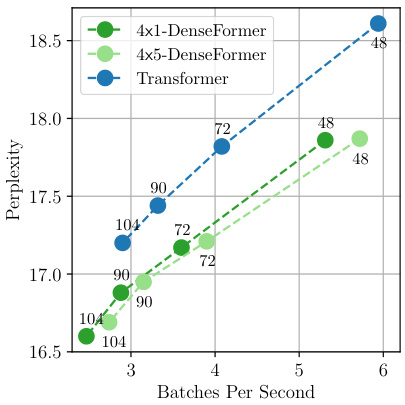
This figure compares the training and inference efficiency of the DenseFormer model against the standard Transformer model for 48 blocks. It demonstrates that DenseFormer achieves a better perplexity/inference speed trade-off. By adjusting the dilation (k) and DWA period (p) hyperparameters, a balance can be struck between perplexity and inference/training speed. The figure shows that 4x5-DenseFormer provides better perplexity than the Transformer baseline in all three aspects (inference speed, training speed, and training time).

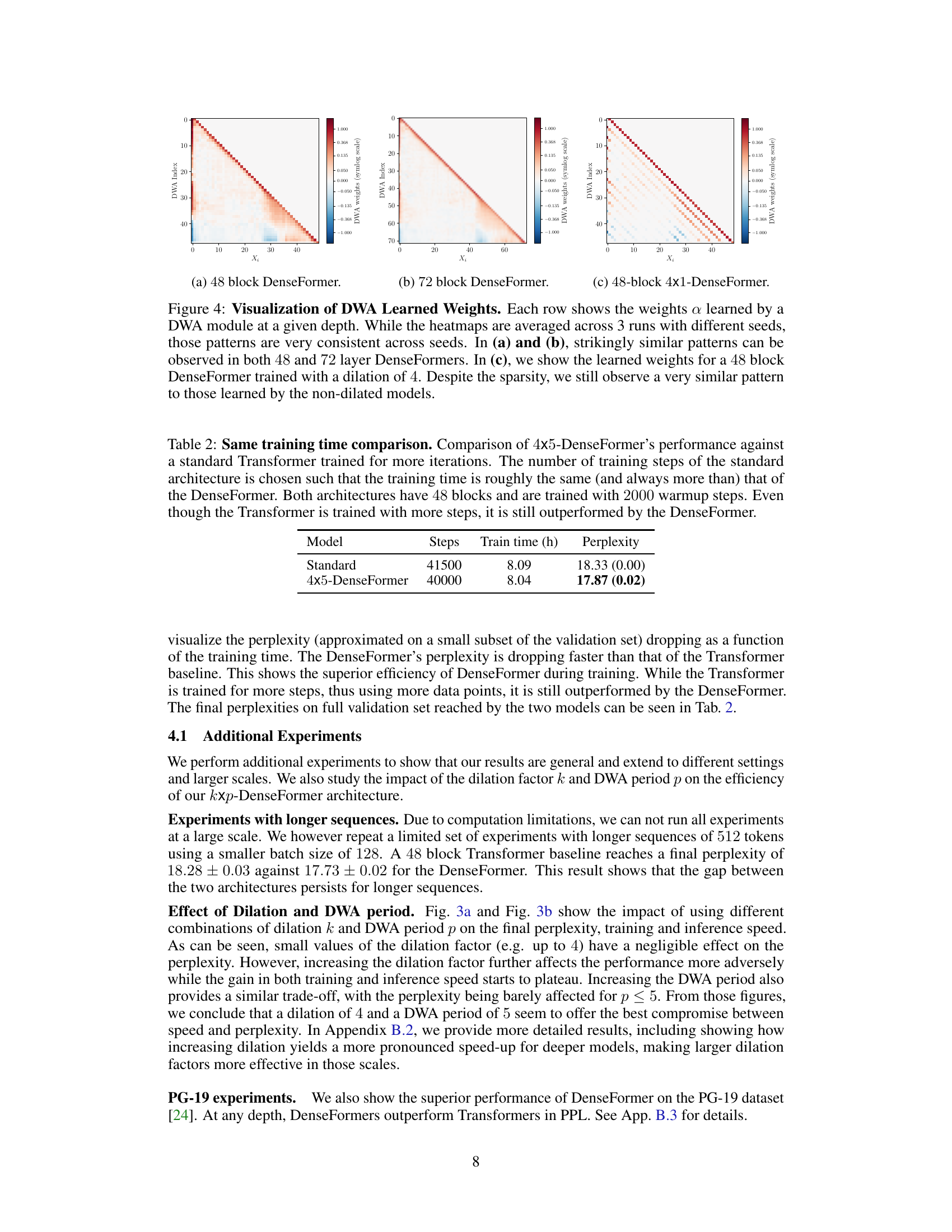
This figure visualizes the learned weights of the Depth Weighted Average (DWA) modules in DenseFormer models with different depths and dilation factors. The heatmaps show that the learned weight patterns are surprisingly consistent across different random seeds and model configurations. The consistent patterns, especially the diagonal and the upper-diagonal weights, reveal how the model effectively reuses information from previous layers. Even with a sparsity-inducing dilation factor of 4, the weight patterns maintain a similar structure.
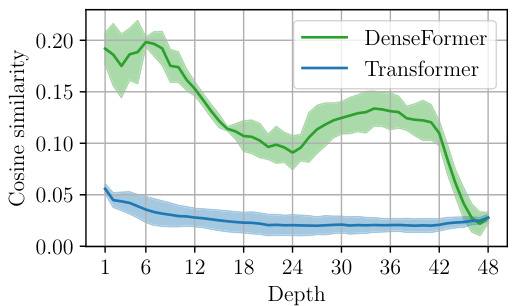
This figure shows the cosine similarity between the output of each Depth Weighted Average (DWA) module and the initial embedding vectors across different depths of the network. The results are averaged across three different random seeds. It shows that the correlation between the DWA module outputs and the input embeddings is initially high but decreases as the depth increases, suggesting a shift in the model’s focus from processing the current token to preparing for the next.

This figure illustrates the DenseFormer architecture, a modification of the standard Transformer architecture. Panel (a) shows a simplified version with two transformer blocks, highlighting how the Depth Weighted Average (DWA) module combines outputs from current and previous blocks. Panel (b) shows a matrix representation of the DWA weights for a 12-layer DenseFormer, illustrating how increasing the dilation parameter reduces the computational cost by sparsifying the weight matrix. The DWA weights, represented by red arrows in (a), are learned during training and determine how much information from previous layers is incorporated into the current representation.

This figure compares the training and inference efficiency of DenseFormer against the standard Transformer architecture. It shows the trade-offs between perplexity and inference/training speed for different models. By adjusting the dilation and DWA period parameters, DenseFormer achieves a balance between improved perplexity and reduced computational overhead. The figure also demonstrates that DenseFormer converges faster to lower perplexity during training than the Transformer baseline.
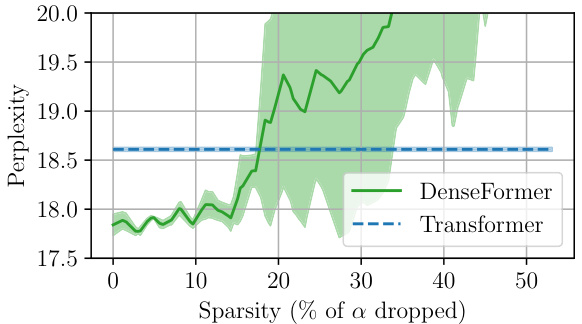
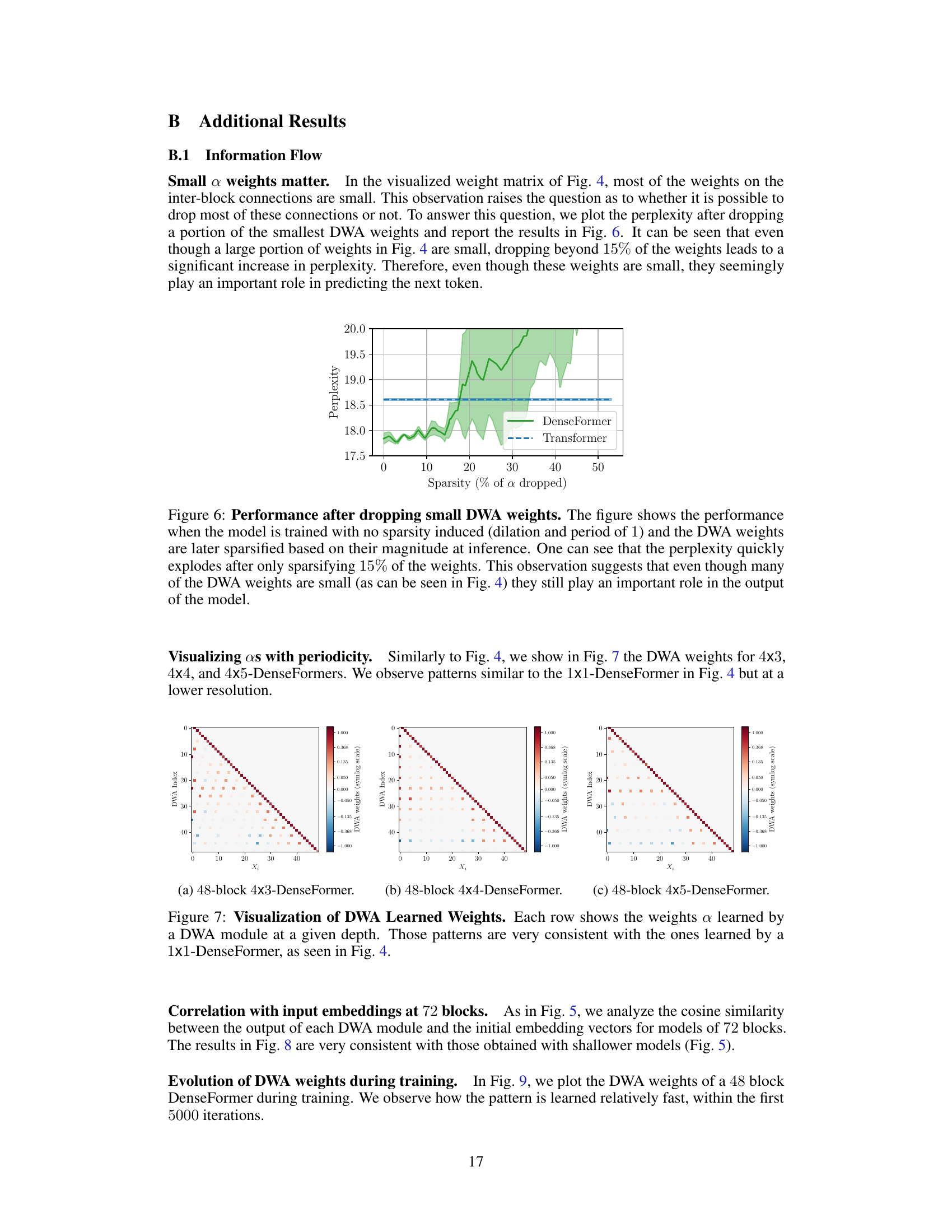
The plot shows the perplexity of a DenseFormer and a standard Transformer model as a function of the sparsity of the DWA weights. The x-axis shows the percentage of the smallest weights that were dropped, and the y-axis shows the perplexity. The plot shows that as the sparsity of the DWA weights increases, the perplexity of both models increases, but the perplexity of the DenseFormer increases more significantly. This suggests that even though many of the DWA weights are small, they still play an important role in the performance of the model.

This figure visualizes the learned weights of the Depth Weighted Average (DWA) modules in DenseFormer for different model depths and with dilation. It shows that the learned weight patterns are surprisingly consistent across different runs with varying random seeds and model configurations (with or without dilation). The consistent patterns observed suggest a structured reuse of activations from distant layers in the network. The figure provides visual evidence supporting the effectiveness of DWA in enhancing information flow.
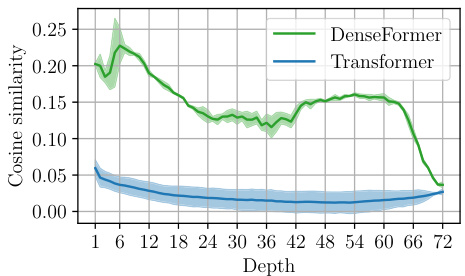
This figure shows the cosine similarity between the output of each Depth Weighted Average (DWA) module and the initial embedding vectors across different depths of the network. The results demonstrate a high initial correlation which gradually decreases in the later layers. This suggests that the model uses input information primarily in earlier layers, and later stages focus on generating the next token.

This figure visualizes the learned weights of the Depth Weighted Average (DWA) modules during the training process. It shows how quickly the weights converge to their final, stable pattern. The heatmaps illustrate the weights at different training steps (0, 1000, 2000, 3000, 4000, 5000, 6000 iterations). After 5000 iterations, the weight pattern closely resembles the stable pattern observed in Figure 4, indicating a rapid learning process.

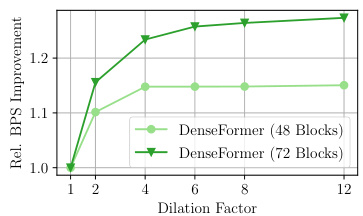
This figure shows the impact of varying the dilation factor (k) on the performance of 48-block and 72-block kx1-DenseFormer models in terms of perplexity and inference speed. The left panel shows a minimal decrease in perplexity until dilation factor 4 after which it decreases significantly. The right panel demonstrates the increase in inference speed relative to a dilation of 1. The gains are larger and the plateau is reached later for the 72-block model. This indicates that small dilation factors offer a good trade-off between perplexity and inference speed.
This figure compares the speed and performance trade-off between the standard Transformer and the 4x1-DenseFormer architectures with varying numbers of blocks (48, 72, 84, and 90). It highlights that the 48-block DenseFormer achieves comparable or better perplexity than much deeper Transformers (up to 90 blocks) while maintaining significantly faster inference speeds. This demonstrates the efficiency gains of the DenseFormer architecture.
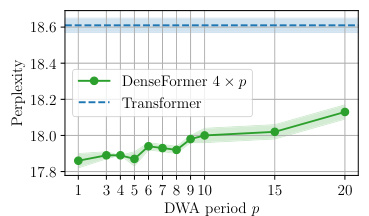
This figure analyzes the impact of varying the DWA period (p) on the performance of 4xp-DenseFormers (where the dilation factor k is fixed at 4) compared to standard Transformers. Part (a) shows that increasing p leads to a slight increase in perplexity, but even with a DWA period of 20, the 4x20-DenseFormer still outperforms the Transformer baseline. Part (b) demonstrates a significant increase in inference speed as p increases, indicating a favorable speed-perplexity trade-off.
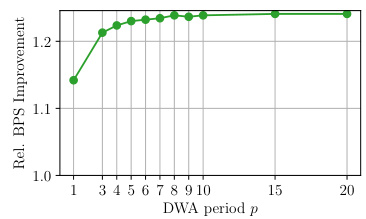
This figure compares the speed and performance trade-off between the standard Transformer architecture and the 4x1-DenseFormer architecture. It shows that for the same level of perplexity, the 4x1-DenseFormer is significantly faster than the standard Transformer. Furthermore, it illustrates that a 48-layer 4x1-DenseFormer achieves comparable perplexity to a much deeper (90-layer) standard Transformer, but with substantially faster inference speeds.
This figure compares the training and inference efficiency of DenseFormer against the standard Transformer architecture using three different metrics: perplexity vs. inference speed, perplexity vs. training speed, and perplexity over training time. The results demonstrate that DenseFormer offers superior performance in terms of perplexity across all three metrics, particularly when using dilation and period hyperparameters for optimization. It showcases the trade-off between speed and perplexity and the ability of DenseFormer to achieve higher performance (lower perplexity) with significantly less time overhead during both training and inference compared to a standard Transformer.

This figure compares the speed and performance trade-off between the standard Transformer and the 4x1-DenseFormer architecture with different numbers of blocks (48, 72, 84, and 90). The results show that the 48-layer DenseFormer significantly outperforms deeper Transformer models in terms of perplexity and achieves comparable performance to a 90-layer Transformer while being 1.6 times faster during inference. This demonstrates the efficiency gains of the DenseFormer architecture.

This figure visualizes the learned weights of the Depth Weighted Average (DWA) modules in DenseFormer for different model depths and dilation settings. The heatmaps show consistent patterns across multiple runs with varying random seeds. The visualization highlights the stable and structured reuse of activations from different layers, even with sparsity introduced through dilation.
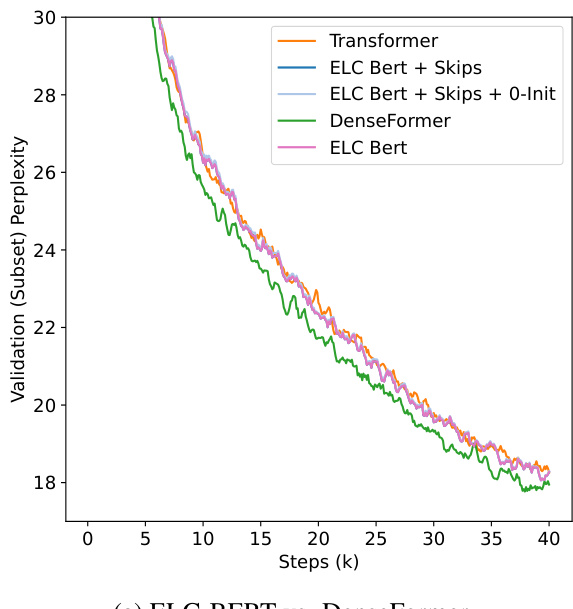
This figure compares the performance of DenseFormer with ELC-BERT, a concurrent work, under different data regimes (low data vs. non-low data). In the low-data regime (part b), ELC-BERT initially outperforms DenseFormer, but DenseFormer quickly catches up and surpasses ELC-BERT’s performance after approximately 1200 steps. In the non-low data regime (part a), DenseFormer consistently outperforms both ELC-BERT and the baseline Transformer.
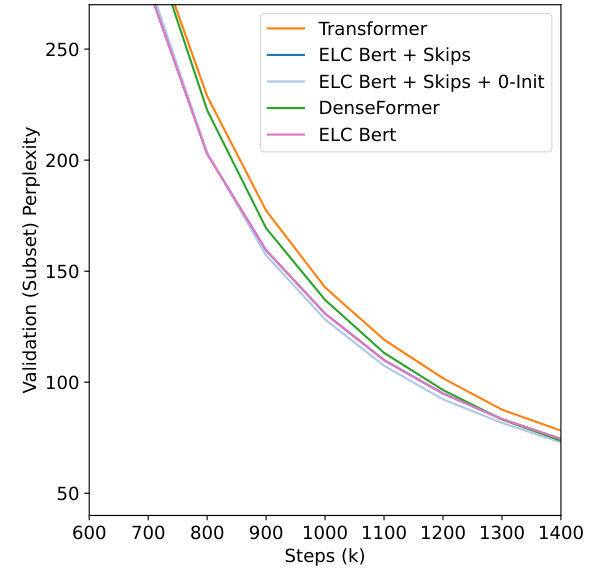
This figure compares the performance of DenseFormer against ELC-BERT, another concurrent work in the same area, under different data regimes. Part (a) shows that in the non low data regime, ELC-BERT performs similarly to the baseline, while DenseFormer consistently performs better. Part (b) shows that ELC-BERT outperforms DenseFormer in a low data regime (as expected, since this is the setting for which ELC-BERT was developed), but DenseFormer quickly catches up and surpasses ELC-BERT’s performance after roughly 1200 iterations.
More on tables

This table compares the performance of DenseFormer and standard Transformer models of different sizes on the OpenWebText2 dataset. The comparison considers several key metrics: number of parameters, perplexity (a measure of model accuracy), and inference speed (measured in batches per second). The results demonstrate that DenseFormer consistently outperforms standard Transformers, especially in terms of inference speed while achieving similar or better perplexity. The impact of increasing the dilation factor and DWA period (two hyperparameters of DenseFormer) on inference speed is also highlighted.

This table compares the performance of DenseFormer and standard Transformer models of different sizes on the OpenWebText2 dataset. The comparison uses perplexity, the number of parameters, and inference speed (measured in batches per second). Results are averaged across three runs with different random seeds. DenseFormer consistently outperforms standard Transformers with the same depth and often outperforms deeper Transformers with similar inference speeds. The table also demonstrates that increasing dilation and DWA period improves inference speed with minimal impact on perplexity. Adding scaling to skip connections in the standard architecture does not replicate DenseFormer’s performance gains, highlighting the importance of DenseFormer’s inter-block connectivity.

This table compares the performance of DenseFormer and standard Transformer architectures of different sizes on the OpenWebText2 dataset. It shows the number of parameters, perplexity, and inference speed (batches per second) for each model. The results demonstrate that DenseFormer achieves lower perplexity and faster inference speed compared to standard Transformers with the same depth or similar inference speed. Increasing the dilation factor and DWA period further improves inference speed with minimal impact on perplexity. The table also shows that simply adding scaling factors to skip connections in the standard Transformer architecture does not produce the same performance gains as DenseFormer, highlighting the importance of DenseFormer’s inter-block connectivity.
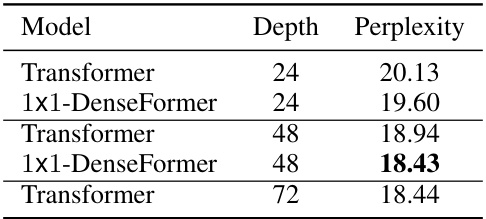
This table compares the performance of DenseFormers and standard Transformers on the PG-19 dataset. It shows the perplexity achieved by each model architecture at different depths (24, 48, and 72 layers). The results demonstrate that DenseFormers consistently outperform standard Transformers in terms of perplexity, showcasing the effectiveness of the proposed architecture across datasets. The batch size used for these experiments was 128.

This table shows the effect of delaying the training of DWA weights. A 4x5-DenseFormer model was trained for 40k iterations. In the experiment, the training was performed as a standard Transformer for N iterations, then switched to DenseFormer training until the 40k iteration mark. The table shows the perplexity achieved for different values of N, demonstrating that starting DWA training earlier yields better performance.

This table compares the performance of DenseFormer and standard Transformer models of various sizes on the OpenWebText2 dataset. Key metrics include the number of parameters, perplexity, and inference speed (batches per second). It demonstrates DenseFormer’s superior performance in terms of perplexity and inference speed compared to standard Transformers of the same depth or similar inference speed. The table also shows that simply adding scaling factors to skip connections in standard Transformers does not achieve the same level of improvement as DenseFormer, highlighting the significance of DenseFormer’s inter-block connectivity.
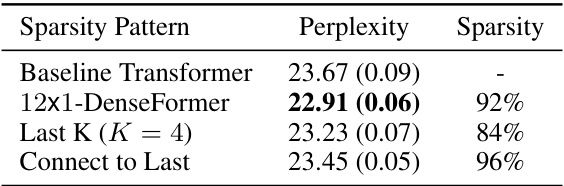
This table compares the performance of DenseFormer and standard Transformer architectures of various depths on the OpenWebText2 dataset. It shows perplexity scores and inference speed (measured in batches per second). The results demonstrate DenseFormer’s superior performance in terms of perplexity and speed compared to standard Transformers at various depths and sizes.
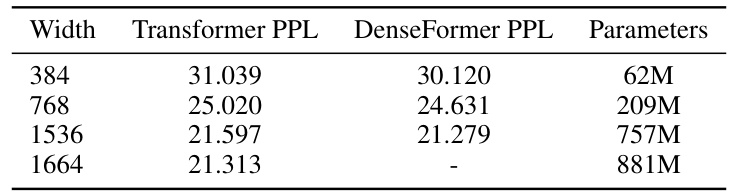
This table compares the performance of DenseFormer and standard Transformer models of various sizes on the OpenWebText2 dataset. It shows the number of parameters, perplexity, and inference speed (batches per second) for each model. The results demonstrate DenseFormer’s superiority in terms of perplexity and inference speed, especially when considering models with similar depths or inference times. The table also highlights the impact of DenseFormer’s architectural improvements, as increasing the dilation factor and DWA period significantly enhances inference speed without sacrificing perplexity.
Full paper#