Generalized Fast Exact Conformalization

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it significantly accelerates conformal prediction, a crucial technique for quantifying uncertainty in machine learning. Its novel approach offers a unified view of existing methods, provides geometric insights, and is broadly applicable to various models. This speeds up model development and deployment, enhancing the reliability of predictions in real-world applications.

Visual Insights

#

The figure illustrates the concept of fast exact conformalization. The left side shows the input data (X, y) and the new data point (Xn+1, Yn+1) to be predicted. The new data point projects into the latent label space Y, where its conformity score is calculated. The red curve represents the solution path across the label space, found using a path-following algorithm, providing a more computationally efficient way to obtain the prediction set compared to conventional methods that require multiple model refits.

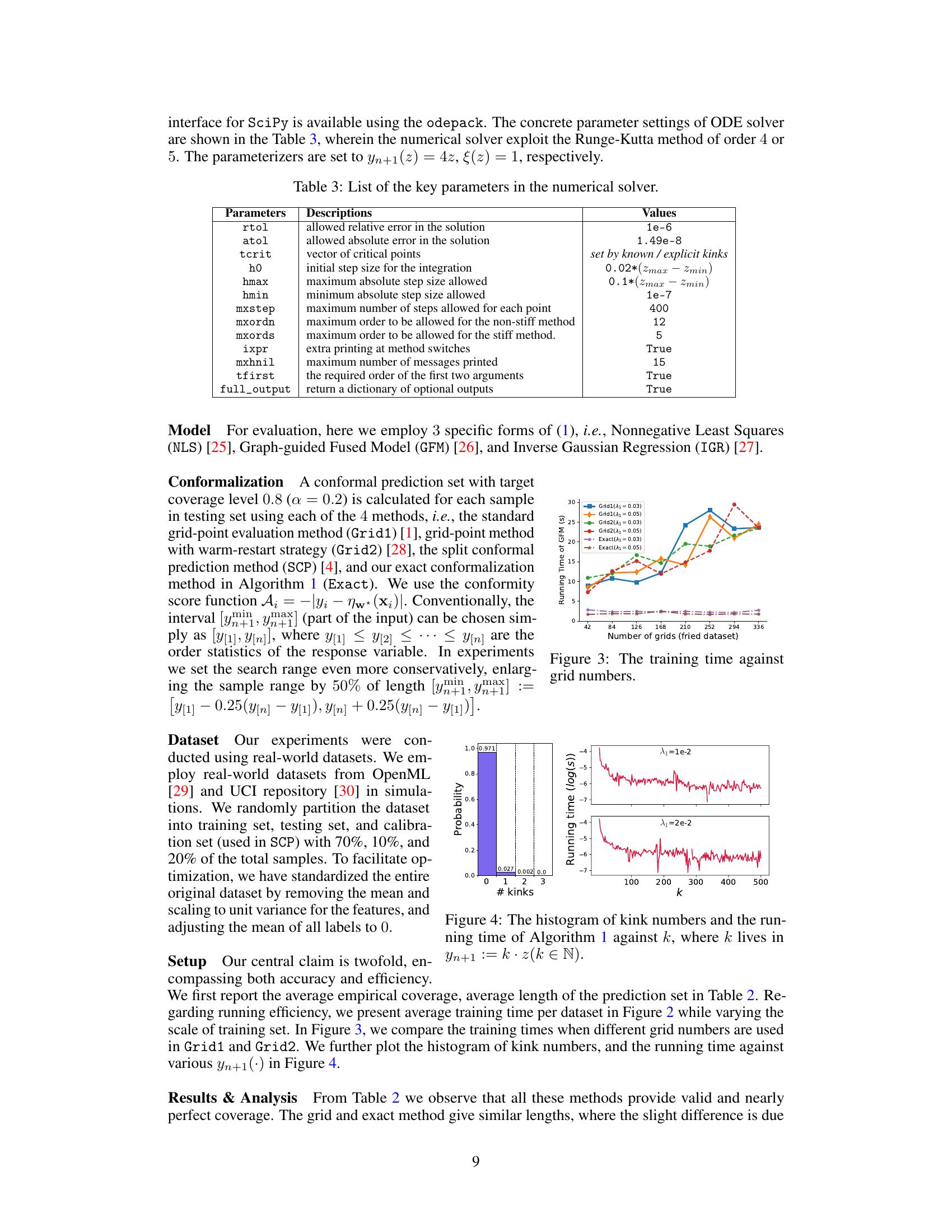
This table compares several existing methods for conformal prediction, highlighting their characteristics. It shows the model used, the reference paper, whether the method provides an exact or approximate solution, the type of loss function and regularizer employed, whether it incorporates constraints, and the structure of the solution path. The table demonstrates that existing methods are either tailored to specific models or rely on approximate solutions. The authors’ proposed method is highlighted as a more general and exact approach with a piecewise smooth solution path.

In-depth insights

#

Fast Conformalization

#

Fast conformalization methods address the computational challenges inherent in traditional conformal prediction, which often requires numerous model retraining steps. The core goal is to significantly reduce the runtime while maintaining the validity of conformal prediction’s coverage guarantees. This typically involves exploiting structural properties of the underlying model or problem, such as smoothness in the solution path. Efficient algorithms may utilize numerical techniques like homotopy methods or clever approximations to navigate the solution space more efficiently. Balancing speed and accuracy is paramount; approximations must be carefully designed to bound the error introduced, ensuring the final prediction intervals still offer reliable coverage. The success of fast conformalization hinges on finding effective trade-offs between computational cost and the statistical guarantees of the method. Generalizability across various models and problem settings is also a crucial factor, expanding the applicability of conformal prediction to more resource-constrained environments.

Path Structure Analysis

#

A crucial aspect of the research lies in its innovative ‘Path Structure Analysis’. This analysis is not merely a descriptive overview, but rather a deep dive into the inherent mathematical structure of the solution path. The authors don’t simply observe the path; they develop a differential equation perspective to understand its underlying dynamics. This approach allows them to reveal the piecewise smooth nature of the solution path, a key finding that enables significant computational gains. This piecewise smoothness is not assumed, but rather rigorously derived from first-order optimality conditions, providing strong theoretical grounding for the methodology’s efficiency. Furthermore, the analysis offers geometric insights, enriching our understanding of the optimization landscape and paving the way for improved algorithmic design. Ultimately, the path structure analysis is pivotal for developing the fast exact conformalization algorithm proposed in the paper, demonstrating that a thorough understanding of fundamental mathematical structures can unlock considerable computational efficiency.

Algorithmic Efficiency

#

Algorithmic efficiency is a critical aspect of any machine learning model, and its importance is magnified in the context of conformal prediction, where the computational cost can quickly become prohibitive. This paper addresses the efficiency challenge head-on by focusing on the inherent structure of the solution path in conformalization. The authors make the crucial observation that this path is piecewise smooth, a property they exploit to dramatically accelerate the process. By leveraging second-order information of difference equations, they’re able to approximate the entire solution spectrum effectively, outperforming the brute-force methods typically employed. The development of a differential equation perspective allows for a generalized framework, adaptable to various statistical models beyond those previously considered. This leads to significant speedups, demonstrated through numerous benchmarks, making the approach not only theoretically sound, but also practically viable for real-world applications. Importantly, the proposed method seamlessly integrates with well-established numerical solvers, reducing implementation complexity and facilitating wider adoption. The combination of theoretical rigor and practical efficiency makes the algorithmic approach a significant contribution to the field of conformal prediction.

Empirical Validation

#

An effective empirical validation section in a research paper should meticulously demonstrate the practical effectiveness of the proposed methodology. It needs to go beyond simply reporting results; it should provide a nuanced analysis of the findings. Strong experimental design is crucial, involving well-defined metrics, appropriate baselines, and sufficient data to ensure statistical significance. The section should clearly describe the datasets used, their characteristics, and any preprocessing steps. Detailed explanations of the experimental setup are essential, such as parameter choices and their justification. Visualizations, such as graphs and tables, should be used to present results clearly and concisely. Furthermore, discussion of both positive and negative findings is necessary, along with exploring potential reasons behind unexpected outcomes. Finally, a robust empirical validation section strengthens the paper’s overall impact by demonstrating the real-world applicability and limitations of the proposed approach.

Future Extensions

#

Future research directions stemming from this work could explore several promising avenues. Extending the framework to handle non-convex loss functions would broaden applicability to a wider range of models and problems. Investigating adaptive methods for selecting the step size in the numerical ODE solver could further enhance computational efficiency. A theoretical analysis of the algorithm’s robustness to violations of the exchangeability assumption is crucial for practical applications. Finally, exploring parallel or distributed implementations to accelerate the processing of large datasets would be highly beneficial, particularly for real-time applications.

More visual insights

#

More on figures

This figure illustrates the core idea of the proposed fast exact conformalization method. It shows how the solution path in the label space can be traced efficiently using a path-following algorithm, avoiding the need for multiple model retraining which is required in the conventional approach. Each point on the red solution path corresponds to a specific label candidate, and the whole path represents the spectrum of solutions.

This figure shows the running time comparison of different conformal prediction methods (Grid1, Grid2, SCP, Exact) under various dataset sizes for three different regression models (NLS, GFM, IGR). The x-axis represents the size of the dataset, while the y-axis represents the running time in seconds. The lines represent the different methods, allowing for a direct visual comparison of their computational efficiency. The results demonstrate that the proposed ‘Exact’ method is significantly faster than other methods, especially as the dataset size increases.

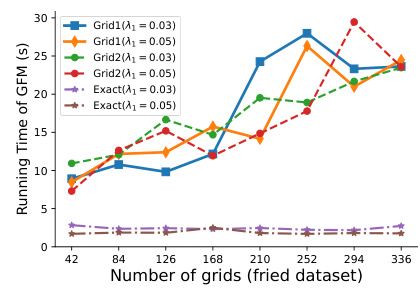
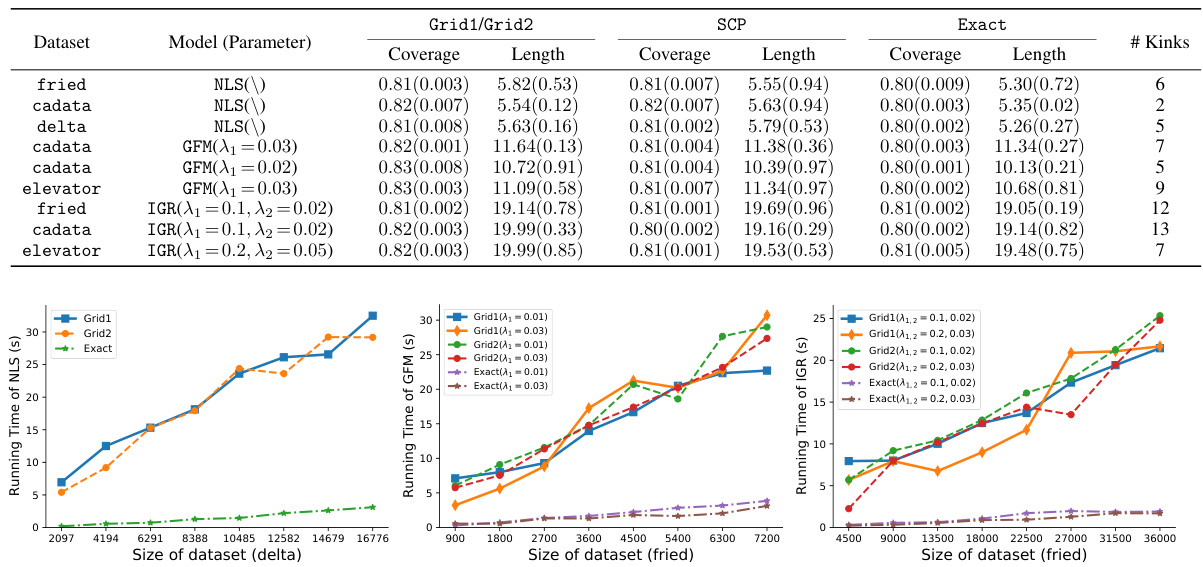
This figure shows the running time of different conformal prediction methods (Grid1, Grid2, Exact, and SCP) as the size of the dataset increases. The x-axis represents the size of the dataset, and the y-axis represents the running time in seconds. Different line styles and colors distinguish between the methods and different parameter settings for regularization strength (λ₁). The results demonstrate that the proposed ‘Exact’ method is significantly faster than the grid-based methods (Grid1 and Grid2), especially as the dataset size grows.

This figure shows two subfigures. The top subfigure is a histogram showing the distribution of the number of kinks encountered during the execution of Algorithm 1. The bottom subfigure is a line plot showing the running time (in logarithmic scale) of Algorithm 1 as a function of k, for two different values of λ1 (a regularization parameter). The x-axis represents the value of k, and the y-axis represents the running time. The plots illustrate the relationship between the number of kinks, the regularization parameter, and the computational efficiency of the algorithm.

Full paper

#