Learning to Price Homogeneous Data

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in data pricing and online learning. It offers novel discretization schemes that improve upon existing methods, especially in high-dimensional settings. The algorithms presented offer a significant step forward in the efficient pricing of homogeneous data, a prevalent challenge in modern data marketplaces. The research also opens avenues for further investigation into asymmetric feedback models and their application to a wider range of online learning problems.

Visual Insights

#

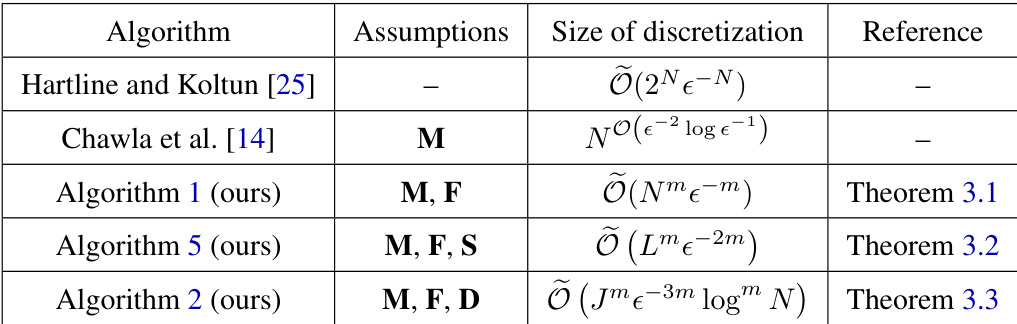
This table compares different discretization schemes for revenue-optimal data pricing, highlighting the assumptions made (monotonicity, finite types, smoothness, diminishing returns), the size of the discretization, and the relevant theorem or reference. It shows that the proposed methods have significantly better dependence on the approximation parameter (epsilon) and the number of data points (N) compared to prior work.

In-depth insights

#

Data Pricing Models

#

Data pricing models are crucial for balancing seller revenue with buyer utility in data marketplaces. Simple models, like fixed pricing per data point, are easy to implement but may not capture the nuances of buyer valuations. More sophisticated approaches consider valuation curves, reflecting how a buyer’s willingness to pay changes with the quantity of data. Dynamic pricing adjusts prices over time, learning from buyer interactions. Mechanism design uses game theory to create optimal pricing strategies considering buyer behavior and information asymmetry. Bayesian approaches incorporate prior knowledge about buyer types or data value distributions to optimize pricing. A key challenge is handling the non-linearity inherent in buyer value for data; discretization and approximation techniques help to make computationally feasible pricing algorithms. Finally, online learning continuously refines pricing strategies through trial and error interactions with the market, but faces challenges like balancing immediate revenue with information gathering to optimize long-term revenue. The choice of model is critically dependent upon market characteristics and the computational resources available to the seller.

Discretization Schemes

#

The effectiveness of online data pricing algorithms hinges significantly on efficient discretization schemes. These schemes approximate continuous pricing curves, which are computationally expensive to handle directly, using a manageable set of discrete price points. The paper explores various discretization strategies, acknowledging the trade-off between approximation accuracy and computational complexity. Monotonicity is a fundamental assumption, enabling the reduction of the price curve space. Beyond this, the paper investigates smoothness and diminishing returns, properties frequently observed in data valuation curves, to further reduce discretization size and improve the algorithm’s efficiency. This careful consideration of discretization significantly enhances the practicality of the proposed data pricing framework and demonstrates a deep understanding of the algorithm’s computational aspects.

Online Learning

#

The research paper explores online learning in the context of dynamic data pricing, a novel problem with asymmetric feedback. The seller learns the optimal pricing strategy by interacting with a sequence of buyers. The learning process is challenging due to the vast space of pricing curves and the limited feedback, as buyers only reveal their type if a purchase is made. The paper develops novel online algorithms, building upon UCB and FTPL but adapting them to handle the unique aspects of the data pricing problem. Regret bounds are derived for both stochastic and adversarial settings, demonstrating the effectiveness of the proposed algorithms. The analysis highlights the need for efficient discretization schemes to represent the pricing curves, which are also a key contribution of the work.

Regret Bounds

#

Regret bounds are crucial for evaluating online learning algorithms. They quantify the difference in performance between an algorithm’s cumulative reward and that of an optimal strategy with full prior knowledge. In the context of data pricing, tight regret bounds are especially important because they directly relate to the seller’s potential revenue loss due to learning the optimal pricing strategy over time. The paper likely analyzes regret bounds in both stochastic and adversarial settings. In the stochastic setting, the buyer types are drawn from a fixed, unknown distribution, which is more realistic and easier to analyze than an adversarial setting. Adversarial settings consider the worst-case scenario with an opponent deliberately choosing sequences of buyer types that maximize the seller’s regret. The effectiveness of discretization techniques directly impacts the regret bounds, with finer discretizations typically leading to smaller regret but higher computational cost. The paper likely explores the trade-off between approximation accuracy and computational complexity when deriving regret bounds. The derived bounds are likely expressed as a function of the number of buyer types (m) and the time horizon (T), illustrating how regret scales with these factors. Smaller regret bounds indicate a more efficient learning algorithm, showing that the algorithm can approach the optimal revenue faster and with less revenue loss.

Future Directions

#

Future research could explore relaxing the assumption of known valuation curves, making the model more realistic by incorporating uncertainty in buyer preferences. Developing algorithms that handle non-homogeneous data would significantly broaden the applicability of this work. Investigating the impact of different feedback mechanisms, beyond the current anonymous setting, is another crucial direction. This could include exploring scenarios where buyers reveal their type regardless of purchase, or where the seller employs discriminatory pricing. Addressing the computational challenges associated with high-dimensional data and a large number of buyer types is crucial for practical implementation. Finally, empirical validation of the proposed algorithms on real-world data marketplaces would be highly valuable to assess their performance and identify areas for further refinement.

More visual insights

#

More on tables

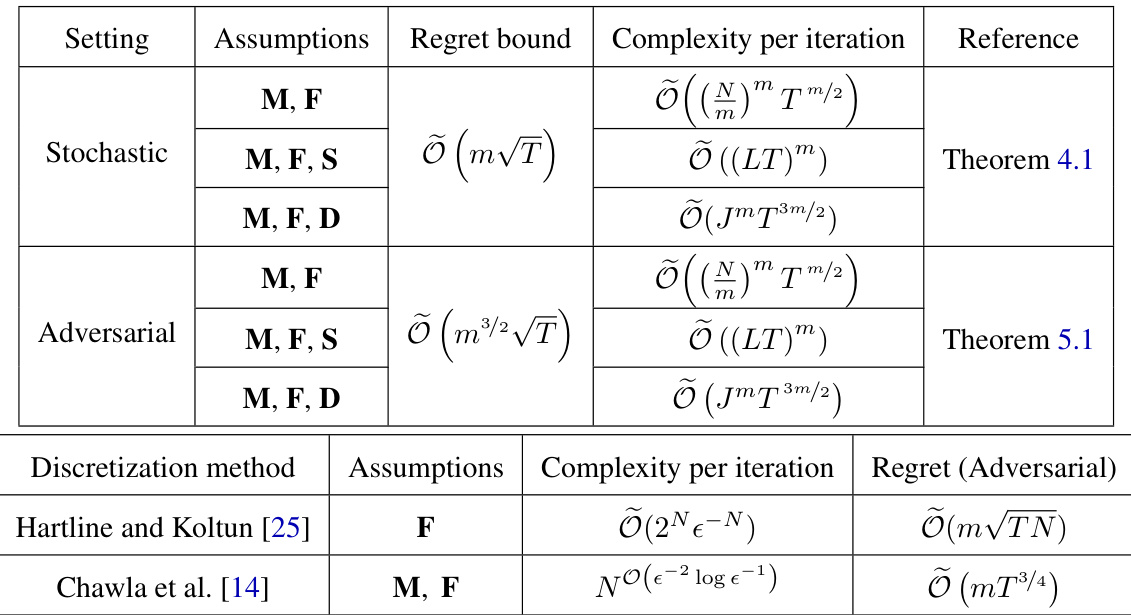
This table compares the regret bounds and computational complexity per iteration of online learning algorithms for data pricing in both stochastic and adversarial settings. It shows the performance of the authors’ algorithms using different discretization schemes under various assumptions (monotonicity, finite types, smoothness, diminishing returns). The results highlight the trade-off between regret and computational cost depending on the setting and assumptions.

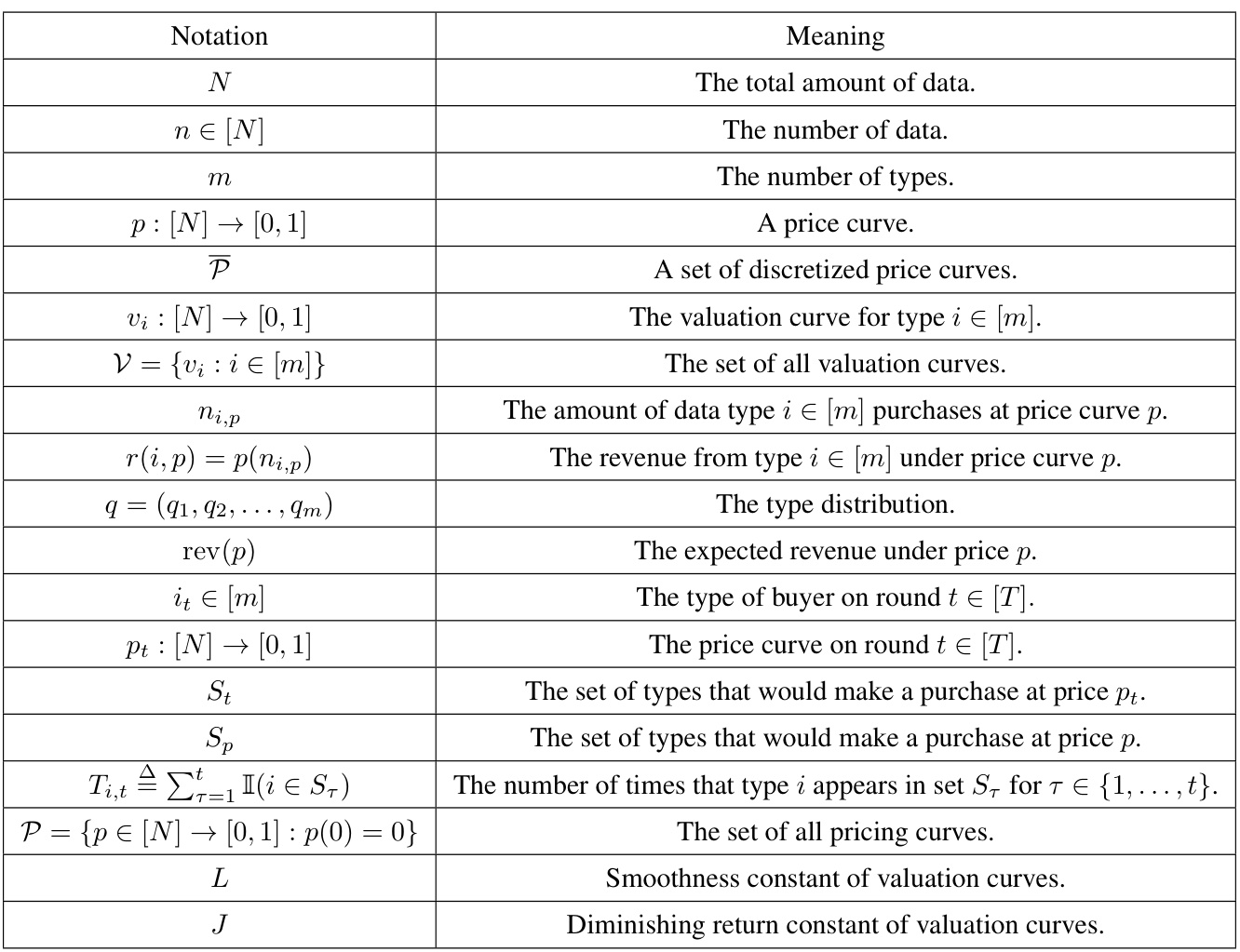
This table compares different discretization schemes for approximating revenue-optimal pricing curves, highlighting the trade-offs between the size of the discretization and the assumptions made about the valuation curves (monotonicity, finite types, smoothness, diminishing returns). It shows that the proposed methods achieve better scaling with the approximation parameter compared to prior work, which is crucial for online learning settings where the parameter needs to approach 0 as the time horizon increases.

Full paper

#