↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Existing Goal-Conditioned Reinforcement Learning (GCRL) algorithms struggle with Non-Markovian Reward (NMR) problems because the Hindsight Experience Replay (HER) technique they rely on cannot effectively densify rewards in such scenarios. This leads to poor policy learning and ineffective curriculum creation. The lack of informative rewards results in many failed trajectories overwhelming the replay buffer.
To overcome these limitations, this paper introduces GCPO, a novel on-policy GCRL framework that is applicable to both MR and NMR problems. GCPO consists of two main components: (1) Pre-training from Demonstrations, which provides an initial goal-achieving capability, and (2) Online Self-Curriculum Learning, which progressively selects challenging goals based on the policy’s current capabilities. The empirical evaluation of GCPO on a challenging multi-goal long-horizon task demonstrates its effectiveness in solving both MR and NMR problems.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on goal-conditioned reinforcement learning, particularly those dealing with non-Markovian reward problems. It offers a novel on-policy framework (GCPO) that surpasses existing off-policy methods, addressing a major limitation in the field. GCPO’s success on complex, real-world tasks opens up exciting new avenues for future research in more challenging scenarios and problem domains.
Visual Insights#

The figure is composed of two parts. The left part illustrates how Hindsight Experience Replay (HER) works on both Markovian Reward (MR) and Non-Markovian Reward (NMR) problems. It shows that HER can successfully densify rewards in MR problems by using a single encountered state as the hindsight goal, but it fails in NMR problems because the reward computation depends on multiple steps of states and actions, and a single state cannot serve as a hindsight goal. The right part presents the experimental results of HER on MR and NMR problems, demonstrating that HER’s performance deteriorates as the NMR’s dependence on consecutive states and actions increases, ultimately becoming indistinguishable from the case without HER. The experiments were conducted on a simplified version of the fixed-wing UAV velocity vector control task.

This table compares the Goal-Conditioned Policy Optimization (GCPO) method with existing HER-based methods. It highlights key differences in the type of reinforcement learning (off-policy vs. on-policy), the types of reward functions they can handle (Markovian Reward (MR) vs. Non-Markovian Reward (NMR)), the methods used to increase informative rewards, and the goal sampling methods employed. The table clarifies that HER-based methods utilize hindsight replay and rely on replay buffers, while GCPO uses pre-training from demonstrations and off-policy evaluation for goal sampling.
In-depth insights#
GCPO Framework#
The GCPO framework presents a novel on-policy approach to Goal-Conditioned Reinforcement Learning (GCRL), significantly diverging from existing off-policy methods reliant on Hindsight Experience Replay (HER). Its core innovation lies in addressing the limitations of HER when dealing with non-Markovian rewards (NMR), a common challenge in real-world applications where reward calculation depends on multiple state-action sequences. GCPO cleverly incorporates pre-training from demonstrations to provide an initial goal-achieving capability, thereby easing the subsequent online learning process and mitigating the issues of failed trajectories often found in HER-based methods. Furthermore, its online self-curriculum learning dynamically adjusts the difficulty of learning goals based on the policy’s evolving capabilities, ensuring effective training progress. This adaptive curriculum generation is crucial for navigating the complexities of both MR and NMR problems, making GCPO a versatile and robust framework for multi-goal reinforcement learning.
NMR Challenges#
Non-Markovian reward (NMR) problems pose significant challenges in Goal-Conditioned Reinforcement Learning (GCRL). Traditional methods like Hindsight Experience Replay (HER) struggle to effectively handle NMRs because the reward’s dependence on multiple past states and actions prevents the simple hindsight goal assignment that makes HER successful in Markovian reward settings. This limitation leads to an abundance of uninformative rewards, overwhelming the replay buffer, and hindering the construction of an effective learning curriculum. Addressing NMRs requires novel approaches that move beyond simple hindsight goal relabeling. The lack of readily available informative rewards necessitates innovative ways to provide sufficient guidance to the learning agent. This might involve crafting more sophisticated reward functions, developing novel exploration strategies to ensure the generation of informative trajectories, or designing entirely new learning algorithms that are inherently better equipped to handle the complexities of non-Markovian reward structures.
Self-Curriculum#
A self-curriculum learning approach in reinforcement learning dynamically adjusts the training difficulty based on the agent’s current performance. It avoids overwhelming the agent with overly challenging tasks early on, focusing instead on a gradual progression. This strategy improves learning efficiency and stability, mitigating issues like catastrophic forgetting and premature convergence. The curriculum’s design is crucial; it must be sufficiently diverse to cover a wide range of scenarios while remaining challenging enough to promote continuous improvement. Effective evaluation metrics are needed to accurately gauge the agent’s skill level and appropriately select the next set of training objectives. Successfully implementing a self-curriculum often necessitates integrating online evaluation methods for continuous assessment and adaptive goal selection. This approach is particularly useful for handling complex tasks that require mastering a wide spectrum of skills and goals.
Pre-training Value#
The concept of “Pre-training Value” in a reinforcement learning context suggests a significant advantage. Pre-training a model on a simpler task or with readily available data before tackling the main, complex objective enhances performance. This is particularly beneficial when dealing with limited data or computationally expensive environments, because the pre-training step imparts an initial level of competence. The resulting policy, already possessing some goal-achieving ability, requires less exploration and may converge more rapidly during the subsequent fine-tuning phase. Effective pre-training can mitigate the challenges of sparse rewards and long horizon problems by providing a stronger starting point for online learning. However, the choice of pre-training data and task is crucial; an inappropriate pre-training regime might hinder, rather than help, the ultimate performance, introducing biases that are difficult to overcome later. Therefore, a thoughtful selection process, considering data relevance and task similarity, is essential for maximizing the pre-training value and achieving the desired overall improvement.
Future of GCPO#
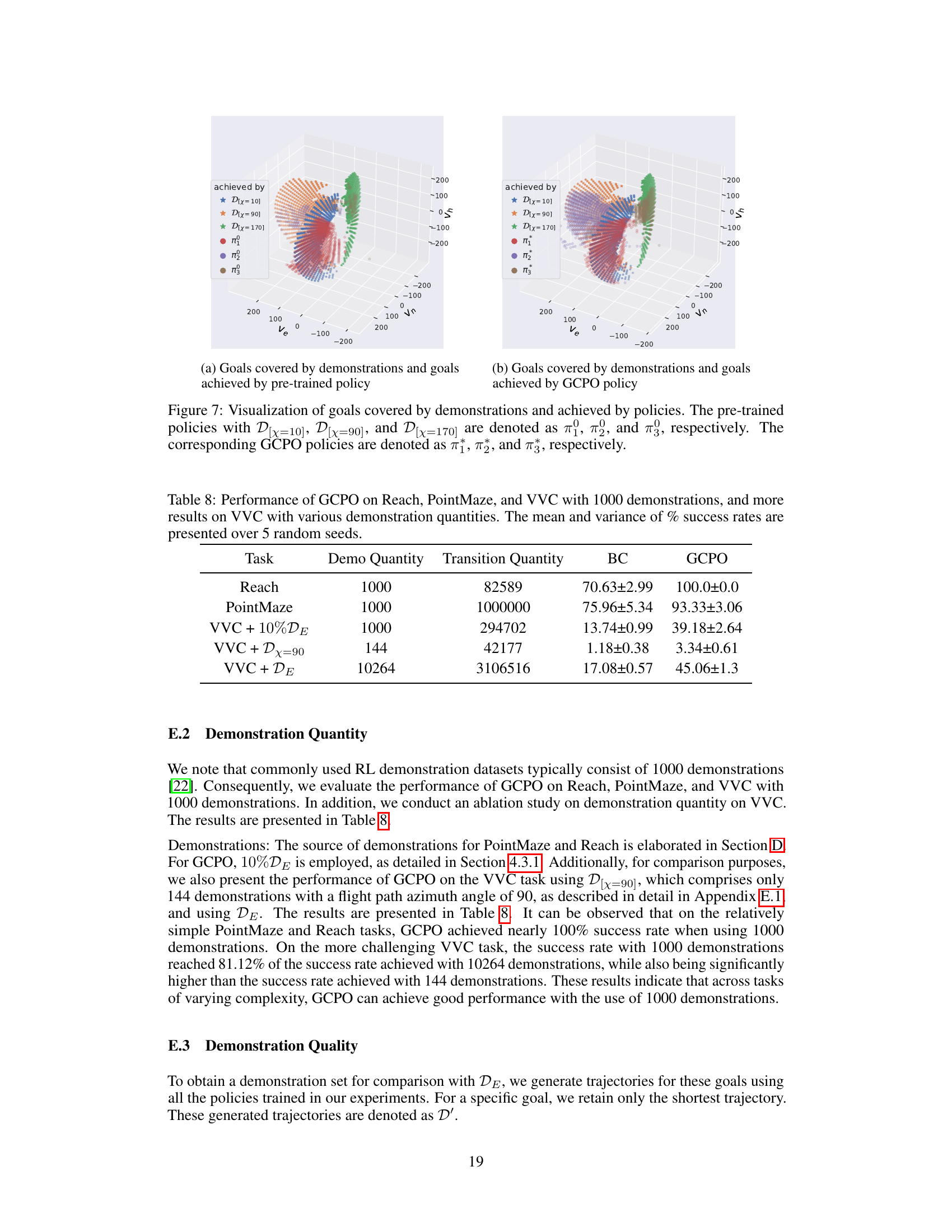
The future of Goal-Conditioned Policy Optimization (GCPO) looks promising, given its demonstrated effectiveness in handling both Markovian and non-Markovian reward problems. Improving the efficiency of the pre-training phase is crucial; exploring more advanced imitation learning techniques or self-supervised methods could significantly reduce the reliance on extensive demonstrations. Expanding the online self-curriculum learning component to incorporate more sophisticated goal selection strategies based on more nuanced estimations of policy capabilities is key to improving adaptability and efficiency. Exploring alternative architectures and algorithms for policy optimization beyond KL-regularized RL could unlock further performance improvements. Addressing scalability challenges associated with handling extremely long horizons or high-dimensional state spaces is essential for real-world applications. Finally, rigorous testing on a broader range of multi-goal tasks, especially more complex real-world problems beyond velocity vector control, will be necessary to fully validate GCPO’s generalizability and robustness.
More visual insights#
More on figures
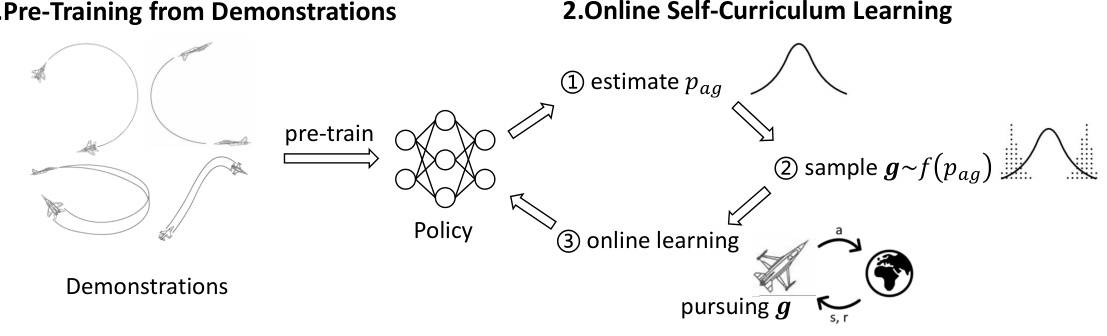
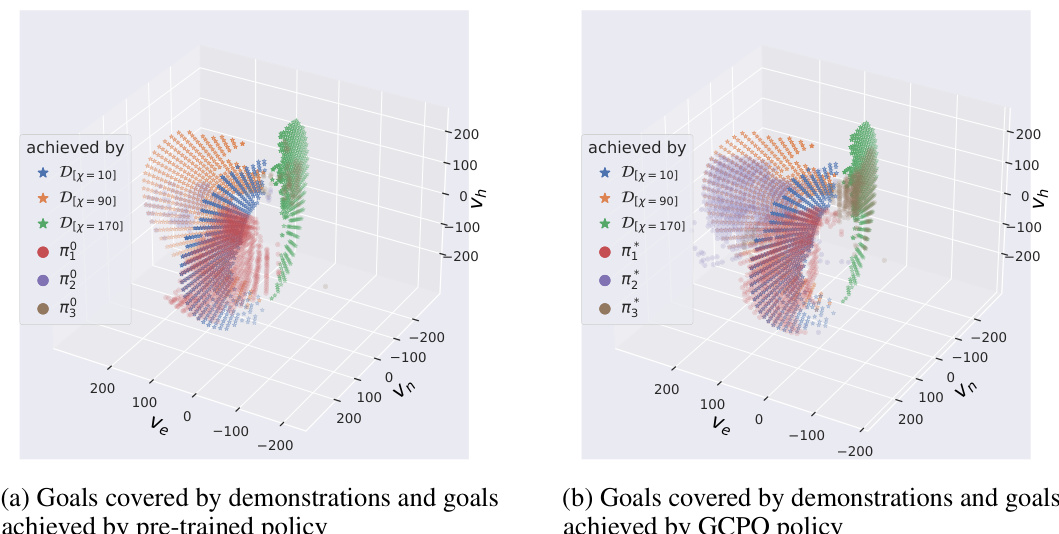
This figure illustrates the GCPO (Goal-Conditioned Policy Optimization) framework, which consists of two main components: Pre-training from Demonstrations and Online Self-Curriculum Learning. The left side shows the pre-training phase, where a policy is pre-trained using demonstrations (illustrated as UAV flight paths). The right side depicts the online self-curriculum learning phase. This involves three steps: (1) Estimating the distribution of achieved goals (pag); (2) Sampling new goals using a probability transform function f (pag, Pdg) to select increasingly challenging goals; and (3) Online learning by pursuing the sampled goals. The overall process iteratively refines the policy’s ability to achieve diverse goals.
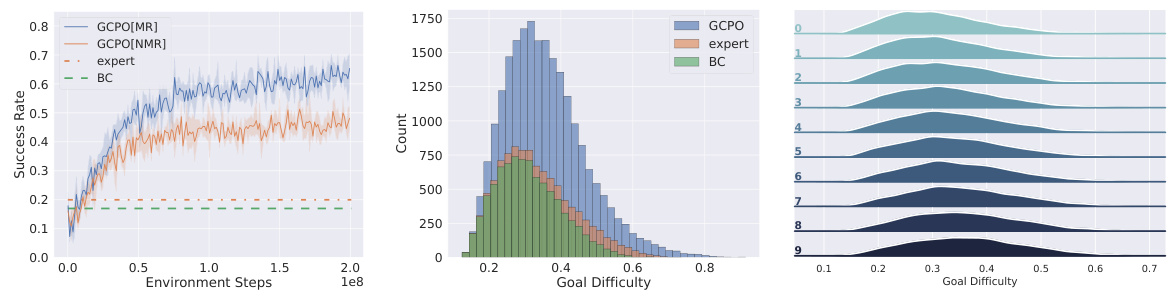
This figure shows the main results of the Goal-Conditioned Policy Optimization (GCPO) method. Subfigure (a) displays the success rate on both Markovian Reward (MR) and Non-Markovian Reward (NMR) problems. Subfigure (b) presents a histogram of the achieved goals. Subfigure (c) illustrates the distribution of goals generated from self-curriculum learning during training. The results demonstrate the effectiveness of GCPO in handling both MR and NMR tasks and highlight the role of online self-curriculum learning in the process.
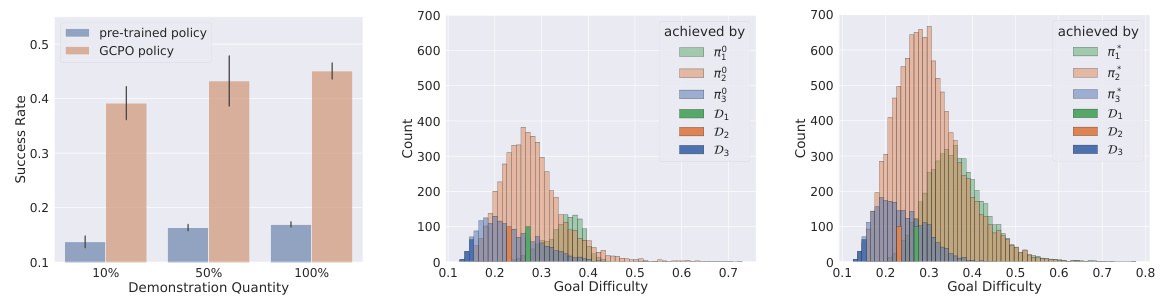
This figure presents the main results of the Goal-Conditioned Policy Optimization (GCPO) algorithm. Subfigure (a) shows the success rate of GCPO on both Markovian Reward (MR) and Non-Markovian Reward (NMR) problems. Subfigure (b) displays a histogram of the achieved goals, illustrating the distribution of goals successfully reached by the algorithm. Subfigure (c) depicts the distribution of goals generated by the online self-curriculum learning component of GCPO during the learning process, demonstrating the algorithm’s ability to adapt the difficulty of goals over time.

This figure presents a comprehensive analysis of different self-curriculum methods’ impact on the GCPO learning process. It compares three distinct self-curriculum learning strategies (RIG, DISCERN, and MEGA) with two non-curriculum approaches (sampling from expert-achievable goals and directly from Pag). The analysis encompasses four subplots: (a) the difficulty of goals sampled by each self-curriculum method over time; (b) the success rate of each method during training; (c) a histogram of achieved goals for various self-curriculum methods; and (d) a comparative histogram of achieved goals for self-curriculum versus non-curriculum methods. The results, generated across five random seeds, offer insights into the effectiveness and distinct characteristics of each goal selection approach.

This figure shows the main results of the Goal-Conditioned Policy Optimization (GCPO) algorithm. Subfigure (a) compares the success rate of GCPO on Markovian Reward (MR) and Non-Markovian Reward (NMR) problems, highlighting GCPO’s success in both scenarios. Subfigure (b) displays a histogram of the achieved goals. Subfigure (c) illustrates the distribution of goals selected by the online self-curriculum learning mechanism of GCPO during the training process.
This figure shows the main results of the Goal-Conditioned Policy Optimization (GCPO) method. Subfigure (a) compares the success rate of GCPO on Markovian Reward (MR) and Non-Markovian Reward (NMR) problems. Subfigure (b) displays a histogram of the achieved goals, illustrating the distribution of goals successfully achieved by the learned policy. Subfigure (c) visualizes the distribution of goals sampled from the self-curriculum learning process during training, highlighting how the algorithm selects increasingly challenging goals as the training progresses.

This figure presents the main results of the GCPO algorithm. Subfigure (a) shows the success rate of GCPO on both Markovian Reward (MR) and Non-Markovian Reward (NMR) problems. (b) displays a histogram of achieved goals, illustrating the distribution of goals successfully achieved during training. Finally, (c) illustrates the distribution of goals selected by the online self-curriculum learning mechanism throughout the training process.
More on tables

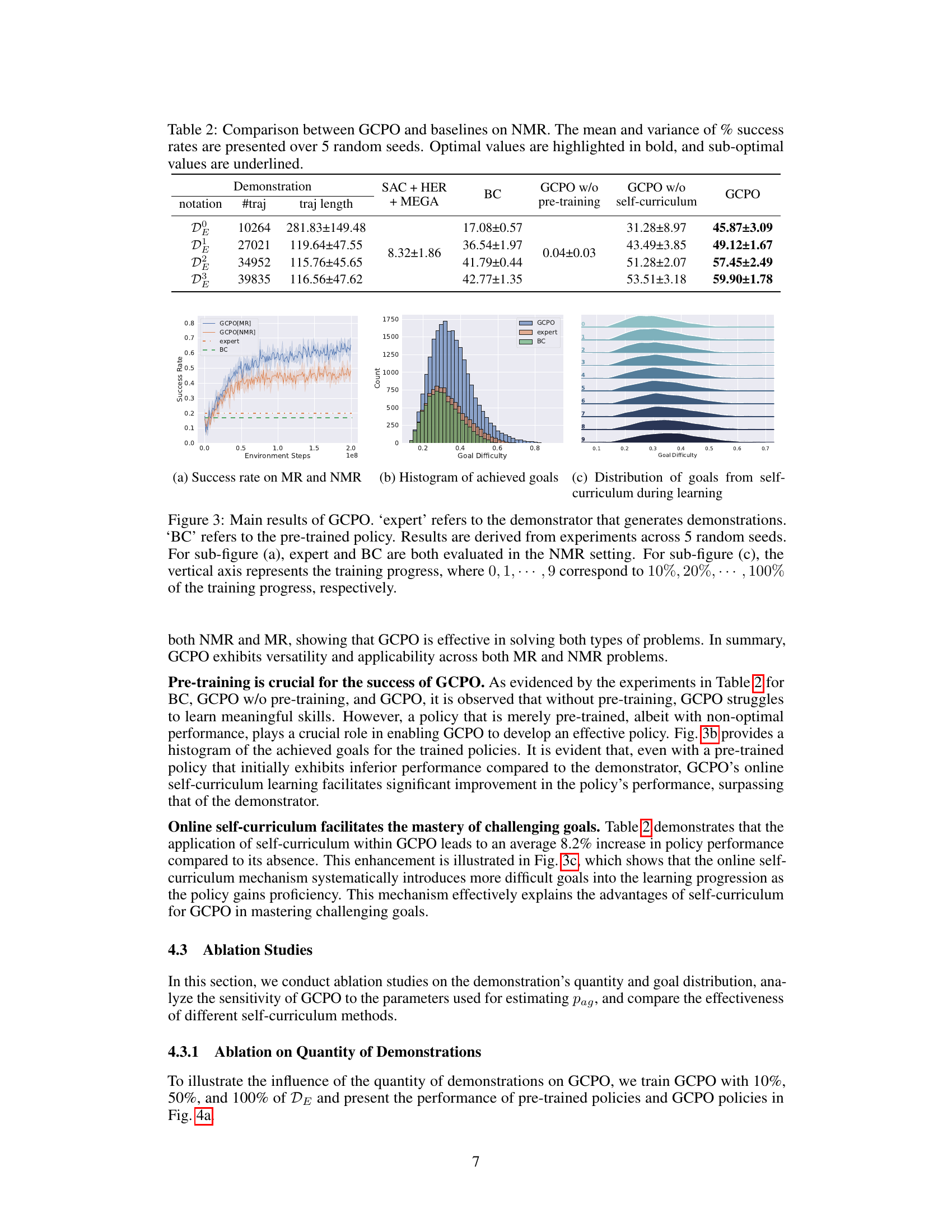
This table compares the performance of GCPO against several baseline methods on a Non-Markovian Reward (NMR) problem. It shows the mean and standard deviation of the success rate (percentage) achieved by each method across five different random seeds. The results are categorized by the quantity and quality of demonstration data used to train the models. Optimal results are highlighted in bold and suboptimal results are underlined, providing a clear visualization of GCPO’s performance relative to baselines under various conditions.

This table compares different goal-conditioned reinforcement learning (GCRL) methods, highlighting the differences between HER-based (off-policy) methods and the proposed GCPO (on-policy) method. It focuses on the type of reinforcement learning (RL), applicable reward types (Markovian or Non-Markovian), methods for increasing informative rewards, and methods for sampling goals. The table shows that GCPO differs significantly from existing HER-based methods by being on-policy and not relying on Hindsight Experience Replay (HER).

This table compares the Goal-Conditioned Policy Optimization (GCPO) framework with existing HER-based methods. It highlights key differences in the type of reinforcement learning (on-policy vs off-policy), the reward types handled (Markovian vs Non-Markovian), methods used for enhancing informative rewards, and the goal sampling strategies employed. The table summarizes how GCPO differs from existing methods by emphasizing its on-policy nature, ability to handle non-Markovian rewards, and its use of pre-training and self-curriculum learning rather than relying on Hindsight Experience Replay (HER).
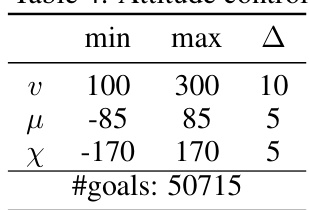
This table compares the performance of GCPO against several baseline methods on a non-Markovian reward (NMR) problem. It shows the mean and standard deviation of success rates across five random seeds for each method, with optimal results highlighted. The table is organized by the quantity and quality of demonstration data used to train the models, providing insights into the effect of varying amounts and qualities of training data on model performance.

This table compares Goal-Conditioned Reinforcement Learning (GCRL) methods, specifically highlighting the differences between HER-based methods (off-policy) and the proposed GCPO method (on-policy). It details the type of reinforcement learning (RL), applicable reward types (Markovian Reward or Non-Markovian Reward), methods for increasing informative rewards, and goal sampling methods used by each algorithm. The table provides a concise overview of existing techniques and how GCPO differs from them.

This table compares the performance of GCPO against several baseline methods (SAC + HER + MEGA, BC) on tasks with Non-Markovian Rewards (NMR). The results, averaged over 5 different random seeds, show success rates (percentage) and their standard deviations. Optimal results are highlighted in bold, and suboptimal results are underlined, demonstrating GCPO’s performance advantage on NMR problems.

This table compares the performance of GCPO against several baseline methods (SAC+HER+MEGA, BC, GCPO without pre-training, GCPO without self-curriculum) on a Non-Markovian Reward (NMR) problem. The results are shown for different quantities and qualities of demonstration data used for pre-training. Success rates are given as mean ± standard deviation across 5 different random seed runs.
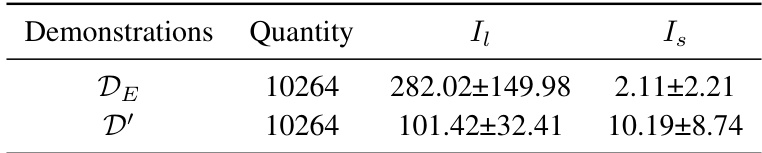
This table compares the performance of GCPO against several baseline methods on a Non-Markovian Reward (NMR) problem. The results are averaged over five random trials. Optimal performance is indicated in bold, while suboptimal results are underlined. Different demonstration sets (DE, DE, DE, D) with varying quantities and lengths are used for training.

This table compares the performance of GCPO against several baseline methods on a Non-Markovian Reward (NMR) problem. The performance metric is the success rate (percentage of successful goal achievements), averaged over 5 random seeds. The table shows the mean and standard deviation of the success rate. Optimal results are shown in bold and suboptimal results are underlined. The table also includes information on the quality and quantity of the demonstrations (training data) used for each method. The goal is to showcase the effectiveness of GCPO in handling NMR problems, compared to existing methods.
Full paper#