↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Generative Flow Networks (GFNs) are powerful generative models but lack consistent control over generating high-utility samples. Existing methods like adjusting temperature parameters are often non-trivial and can negatively impact sample diversity. This work addresses these issues.
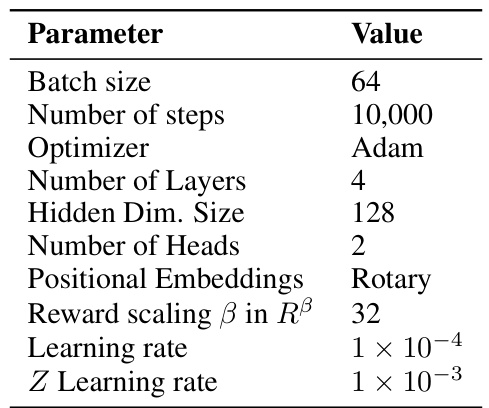
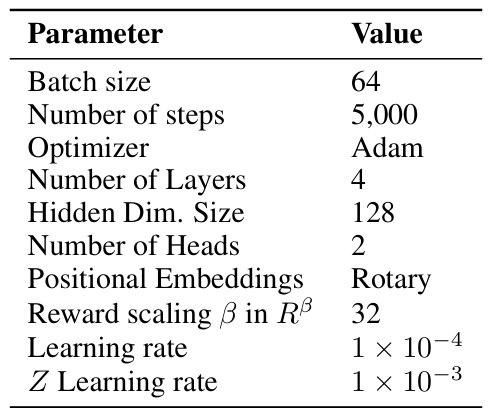
The authors propose QGFN, combining GFNs with reinforcement learning’s action-value estimates. Three QGFN variants (p-greedy, p-quantile, and p-of-max) are introduced, each offering a different approach to balancing exploration and exploitation via a mixing parameter. Empirical results show that QGFN significantly improves high-reward sample generation on diverse tasks, demonstrating its effectiveness and flexibility in controlling the trade-off between reward and diversity at both training and inference time.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in generative modeling and reinforcement learning. It bridges the gap between these two fields by introducing QGFN, a novel method that improves the quality of samples generated by GFNs. This opens avenues for enhanced control and efficiency in generating diverse, high-utility samples for various applications, impacting diverse fields such as drug discovery and material design. The exploration of inference-time-adjustable greediness is also significant, offering a more flexible approach than existing techniques.
Visual Insights#

This figure illustrates a scenario where an agent chooses between two doors. Behind one door are many doors with small rewards (1), while behind the other is a single door with a large reward (100). GFNs, based on flow functions, would assign equal probability to both doors, spending time sampling small rewards. However, a reinforcement learning (RL) agent, using action values (Q), would immediately choose the door with the large reward. This highlights the limitation of relying solely on GFNs for generating high-reward samples and introduces the motivation for combining GFNs with RL action values to create a more effective sampling strategy.

This table presents the results of a comparison of different methods for fragment-based molecule generation after training. The methods compared are GFN-TB, GFN-SUBTB, LSL-GFN, p-greedy QGFN, p-of-max QGFN, and p-quantile QGFN. For each method, the table shows the average reward and diversity, which are calculated at inference time after the models are trained. The reward is a measure of the quality of the generated molecules, while the diversity is a measure of how different the generated molecules are from each other. The results show that the QGFN methods achieve higher average rewards and lower average diversity than the baseline methods. The p-of-max QGFN achieves the highest average reward, while the p-quantile QGFN achieves the lowest average diversity.
In-depth insights#
QGFN: A Deep Dive#
A deep dive into QGFN (Quantile Generative Flow Networks) would explore its core innovation: combining generative flow networks (GFNs) with action-value estimates (Q-functions) from reinforcement learning. This hybrid approach tackles the challenge of consistently biasing GFNs towards high-utility samples, a limitation of traditional GFNs. The key is the introduction of a mixing parameter to control the greediness of the sampling policy, offering a balance between exploration (diversified sampling) and exploitation (focused high-reward sampling). A deep dive would analyze the different QGFN variants (p-greedy, p-quantile, p-of-max), investigating their unique properties and optimal use cases. The effectiveness of QGFN relies heavily on the interplay between the GFN’s ability to explore the state space and the Q-function’s ability to guide towards high-reward regions. Analysis of the training process and the impact of various hyperparameters would be crucial, including the n-step return approach in Q-learning, to ensure a comprehensive understanding of QGFN’s strengths and limitations.
Greedy Sampling#
Greedy sampling methods, in the context of generative models like GFlowNets, aim to efficiently explore high-reward regions of the search space. While a purely greedy approach might get stuck in local optima, the key is to balance exploration and exploitation. Effective greedy sampling techniques often leverage auxiliary information, such as action-value estimates (Q-values), to guide the search toward promising areas, but also retain the ability to explore less-visited areas, thereby mitigating the risk of premature convergence. This balance often involves using a mixing parameter which controls the degree of greediness, allowing the algorithm to adapt its strategy during inference. Controllable greediness is crucial; it prevents a total collapse to the highest-reward areas found, while maintaining the desirable focus on high-reward areas. This is vital for applications requiring both high utility and diversity in the generated samples.
QGFN Variants#
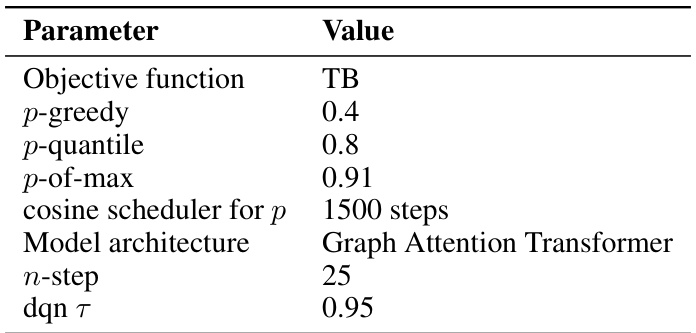
The exploration of QGFN variants reveals a crucial design aspect for balancing exploration and exploitation in generative models. The core idea is to modulate the greediness of sampling through a mixing parameter (p) that combines the GFN policy (PF) with action-value estimates (Q). Three variants are proposed: p-greedy, p-quantile, and p-of-max. Each variant offers a unique way to incorporate Q into the sampling process, thereby controlling the exploration-exploitation trade-off. The p-greedy variant directly mixes PF and a greedy policy derived from Q, offering a simple yet effective balance. P-quantile employs a more aggressive approach by masking actions with low Q-values, creating a controlled search space. Lastly, p-of-max uses a threshold determined by the highest Q-value multiplied by p, providing a dynamic pruning strategy. This thoughtful design allows for fine-grained control over greediness at inference time without retraining, demonstrating the power of QGFN’s flexible framework for tackling diverse tasks.
Method Analysis#
A thorough method analysis section would delve into the rationale behind design choices, exploring the impact of key hyperparameters (like the mixing parameter ‘p’ and the n-step return in Q-learning) on both training stability and the final model’s performance. It would also discuss the selection of specific QGFN variants (p-greedy, p-quantile, p-of-max), justifying their inclusion based on their strengths and weaknesses in different scenarios and task types. A key aspect would be evaluating the effectiveness of combining the GFlowNet policy and Q-function, examining whether the Q-function helps provide a good balance between greediness and exploration. Crucially, an analysis should probe the extent to which the Q-function’s accuracy affects model outcomes, comparing Q-estimates against empirical measures. The section should also investigate the impact of inference-time adjustments, explaining how changing ‘p’ allows for fine-tuning greediness without retraining. Finally, a robust method analysis section must acknowledge and address limitations such as the computational cost associated with training two separate models, and the inherent sensitivity to the accuracy of the Q-function estimation.
Future Research#
The paper’s “Future Research” section hints at several promising avenues. Exploring more sophisticated combinations of Q and PF, perhaps incorporating advanced RL techniques like Monte Carlo Tree Search (MCTS), could significantly improve sampling efficiency and the quality of generated samples. Investigating constrained combinatorial optimization problems by using Q to predict properties or constraints rather than just rewards would enable the generation of objects meeting specific criteria, opening up new applications. A key area for future work is thoroughly investigating the impact of different hyperparameter schedules on model performance and the stability of the training process. This includes exploring adaptive strategies for choosing the greediness parameter (p) during training and exploring more nuanced interactions between the two models. Finally, a deeper exploration of the theoretical underpinnings and limitations of the proposed framework, such as the impact of various reward functions and the effectiveness of different Q-learning strategies, is necessary to better understand the full potential and limitations of this approach.
More visual insights#
More on figures
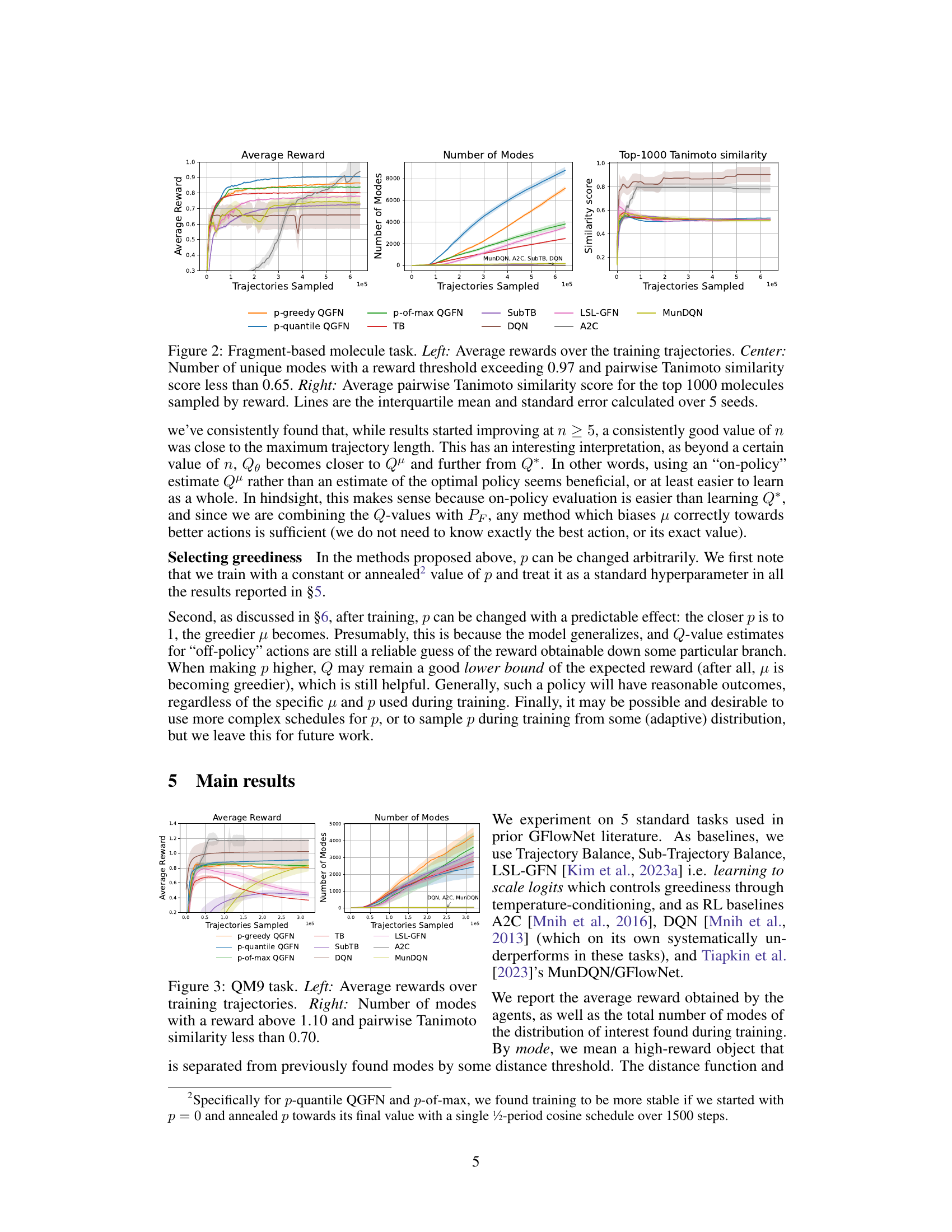
This figure shows the results for the fragment-based molecule generation task. The left panel displays the average rewards obtained over training trajectories for different methods, showing QGFN’s improved performance. The center panel illustrates the number of unique modes discovered (high-reward molecules with low similarity), highlighting QGFN’s enhanced ability to find diverse solutions. The right panel presents the average pairwise Tanimoto similarity scores among the top 1000 molecules, indicating that QGFN also maintains diversity among high-reward molecules.
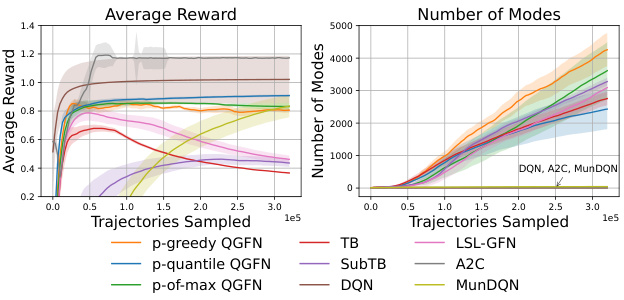
This figure presents the results of the fragment-based molecule generation task. The left panel shows the average rewards obtained over several training trajectories, comparing the QGFN variants (p-greedy, p-quantile, p-of-max) with several baselines (TB, SubTB, DQN, LSL-GFN, A2C, MunDQN). The center panel displays the number of unique modes (high-reward molecules with low similarity) discovered by each method. Finally, the right panel illustrates the average pairwise Tanimoto similarity of the top 1000 molecules sampled by each method, indicating the diversity of the generated molecules. The lines represent the interquartile mean and standard error, calculated from 5 independent trials.
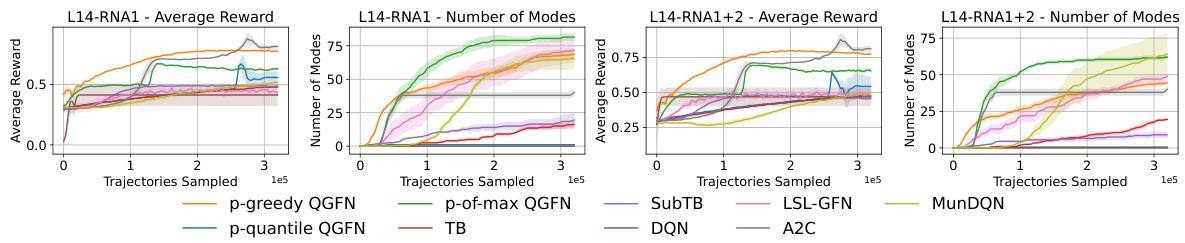
This figure shows the results of RNA-binding tasks using different methods, including QGFN variants and baselines. The left panel presents results for the L14RNA1 task, while the right panel shows results for the L14RNA1+2 task. The plots display average reward and the number of modes discovered by each method across multiple runs (seeds). Error bars represent interquartile ranges, indicating the spread of results. The figure demonstrates the comparative performance of QGFN variants (p-greedy, p-quantile, and p-of-max) against several baselines (TB, SubTB, DQN, LSL-GFN, MunDQN, and A2C) in terms of both reward and mode discovery.
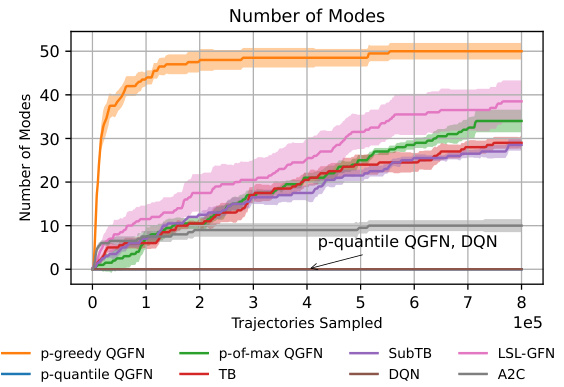
This figure presents the results for a fragment-based molecule generation task. The left panel shows the average rewards obtained over the training trajectories for various methods. The central panel illustrates the number of unique modes discovered (molecules with rewards above 0.97 and dissimilarity above 0.65), while the right panel displays the average pairwise Tanimoto similarity for the top 1000 molecules generated, reflecting the diversity of the samples produced.
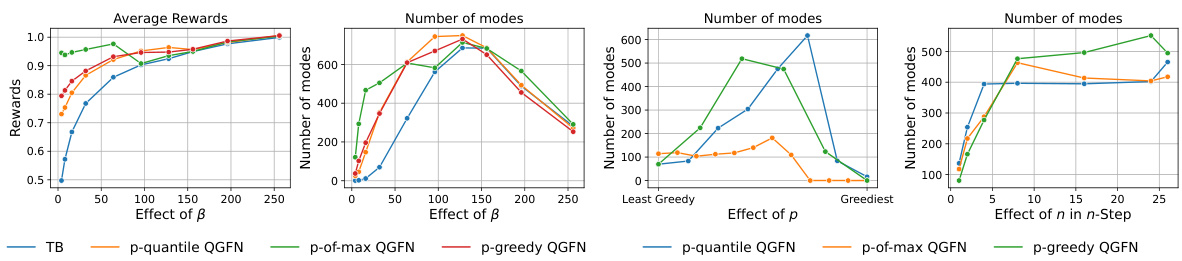
This figure demonstrates the impact of hyperparameters β, p, and n on the performance of QGFN and a baseline GFN model on a fragment-based molecule generation task. The left panel shows that increasing the temperature parameter (β) in both QGFN and GFN leads to higher average rewards but can cause a diversity collapse in the GFN, which QGFN mitigates. The right panel illustrates the effect of the greediness parameter (p) and n-step returns (n) on QGFN performance. Adjusting p allows controlling greediness, while increasing n generally improves both reward and diversity.
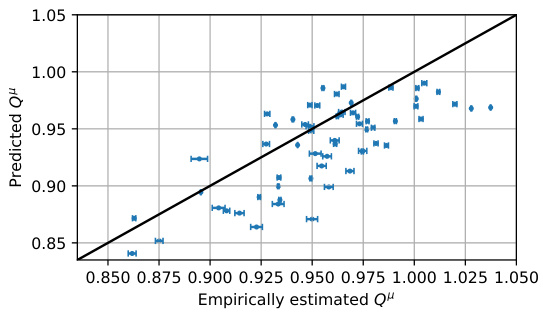
This figure shows the comparison between the predicted Q-values (Q(s, a; 0)) and their empirically estimated counterparts (Qμ). The Q-values are the predictions from the trained action-value function Q, while Qμ is obtained via rollouts using the policy corresponding to the Q-values. Each point represents a state-action pair (s, a), with the x-coordinate being the empirically estimated Qμ and the y-coordinate being the predicted Q(s, a; 0). Error bars represent the standard error for the empirical Qμ estimates. The plot shows a reasonably strong positive correlation between the predicted and empirical Q-values, indicating that the learned Q-function is relatively capable of estimating the expected rewards under the corresponding policy. This supports the validity of using the Q-function to guide the generation process in QGFN.
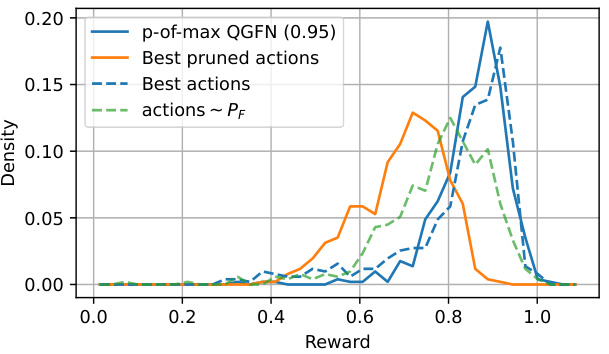
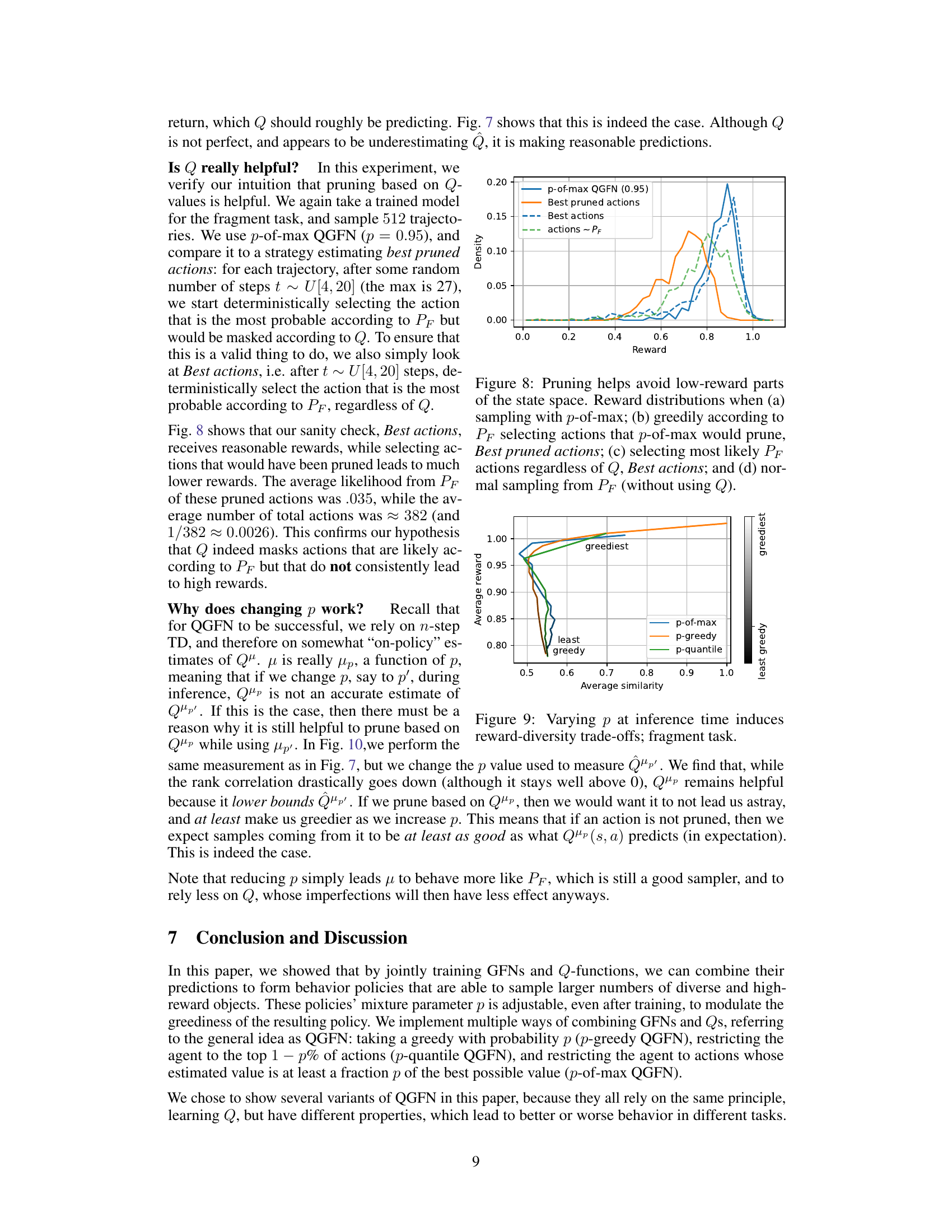
This figure compares reward distributions obtained from different sampling strategies. The x-axis represents the reward, and the y-axis shows the density of samples with that reward. Four scenarios are depicted: (a) p-of-max QGFN (0.95): Samples are generated using the p-of-max QGFN approach with p=0.95, which prunes actions with low Q-values (action-value estimates). This strategy concentrates samples in high-reward regions. (b) Best pruned actions: Actions are greedily selected according to the forward policy (PF) but pruning actions with low Q values based on a pretrained p-of-max QGFN model. This shows that the Q function in the model helps to achieve higher rewards. (c) Best actions: Actions are selected greedily according to the forward policy PF. Without considering Q, more samples are drawn from low-reward regions. (d) actions ~ PF: Shows the baseline reward distribution if only the forward policy PF is used for sampling, with no pruning or greedy action selection based on Q-values.
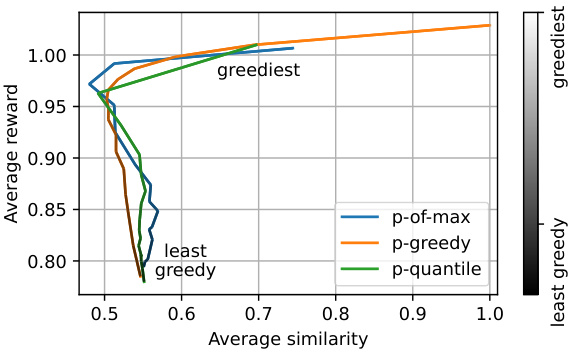
This figure demonstrates the impact of changing the parameter ‘p’ during inference on the reward and diversity of samples generated by the QGFN model in the fragment-based molecule generation task. The x-axis represents the average pairwise Tanimoto similarity, a measure of diversity (lower values indicate higher diversity), and the y-axis represents the average reward (higher values are better). Three QGFN variants (p-greedy, p-quantile, and p-of-max) are shown, each with a range of p values. The color gradient in the legend indicates the range from least greedy (dark grey) to greediest (light grey). The figure shows that by adjusting the ‘p’ parameter, it’s possible to achieve various trade-offs between reward (greediness) and diversity. Higher ‘p’ values tend towards higher rewards but lower diversity, while lower ‘p’ values lead to lower rewards but higher diversity.
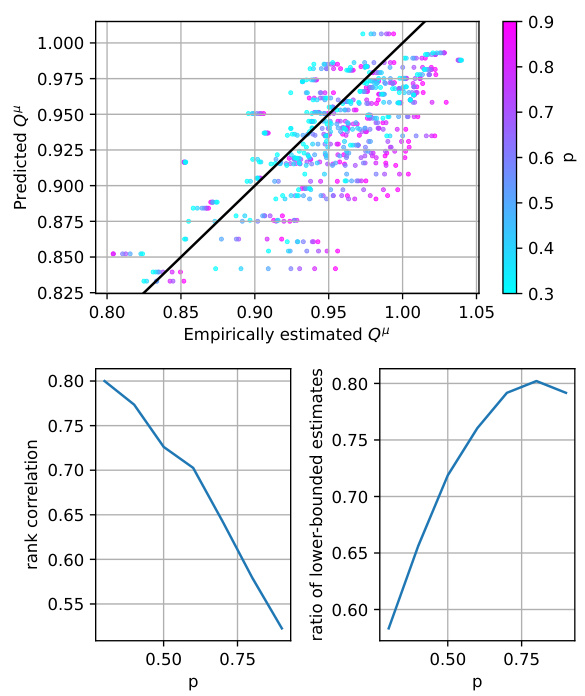
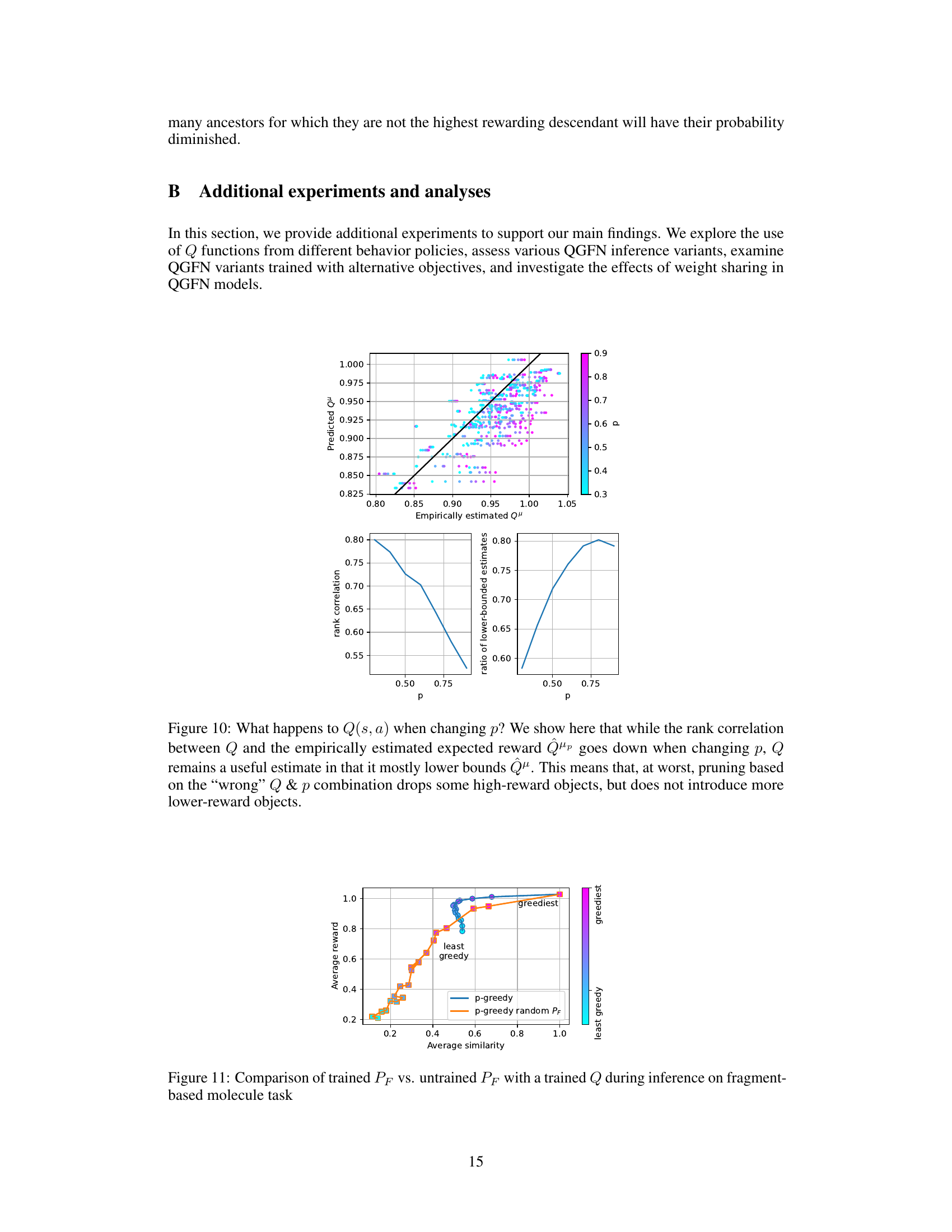
This figure presents a comparison between the predicted Q-values from a trained Q-network and empirical Q-values obtained through rollouts. The plot on the top shows a scatter plot where each point represents a state-action pair, with the x-coordinate representing the empirical Q-value (obtained by averaging the returns from multiple rollouts starting from that state-action pair) and the y-coordinate representing the predicted Q-value from the model. The color of each point corresponds to the value of p (the greediness parameter) used during training. A diagonal line represents perfect correspondence between predicted and empirical Q-values. The plot shows that the predicted Q-values are reasonably close to the empirical Q-values, indicating that the Q-network is relatively capable of estimating the returns of the corresponding policy. The bottom plots further analyze the relationship between the predicted and empirical Q-values by showing the rank correlation and the ratio of lower-bounded estimates as a function of p. The rank correlation plot shows that the rank ordering of Q-values predicted by the model is well-aligned with that from the rollouts, with the correlation reducing as the greediness parameter p increases. The ratio of lower-bounded estimates indicates the extent to which the model underestimates the actual value, which also increases with p.
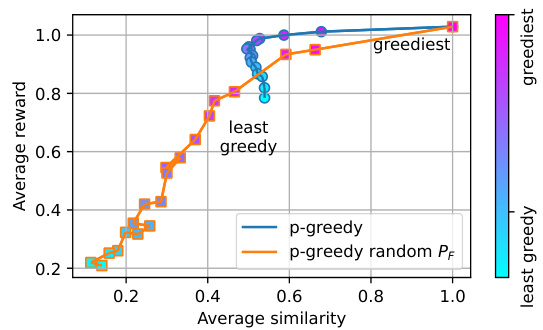
This figure shows the impact of changing the greediness parameter ‘p’ during inference on the average reward and average similarity of the generated molecules in the fragment-based molecule generation task. The x-axis represents the average pairwise Tanimoto similarity, a measure of diversity, and the y-axis represents the average reward. The two lines represent two variants of the QGFN method: one using the trained forward policy (PF), and another using a random forward policy. The color gradient indicates the level of greediness controlled by ‘p’, ranging from least greedy (light cyan) to greediest (magenta). The figure demonstrates the tunable trade-off between reward and diversity introduced by the QGFN approach.

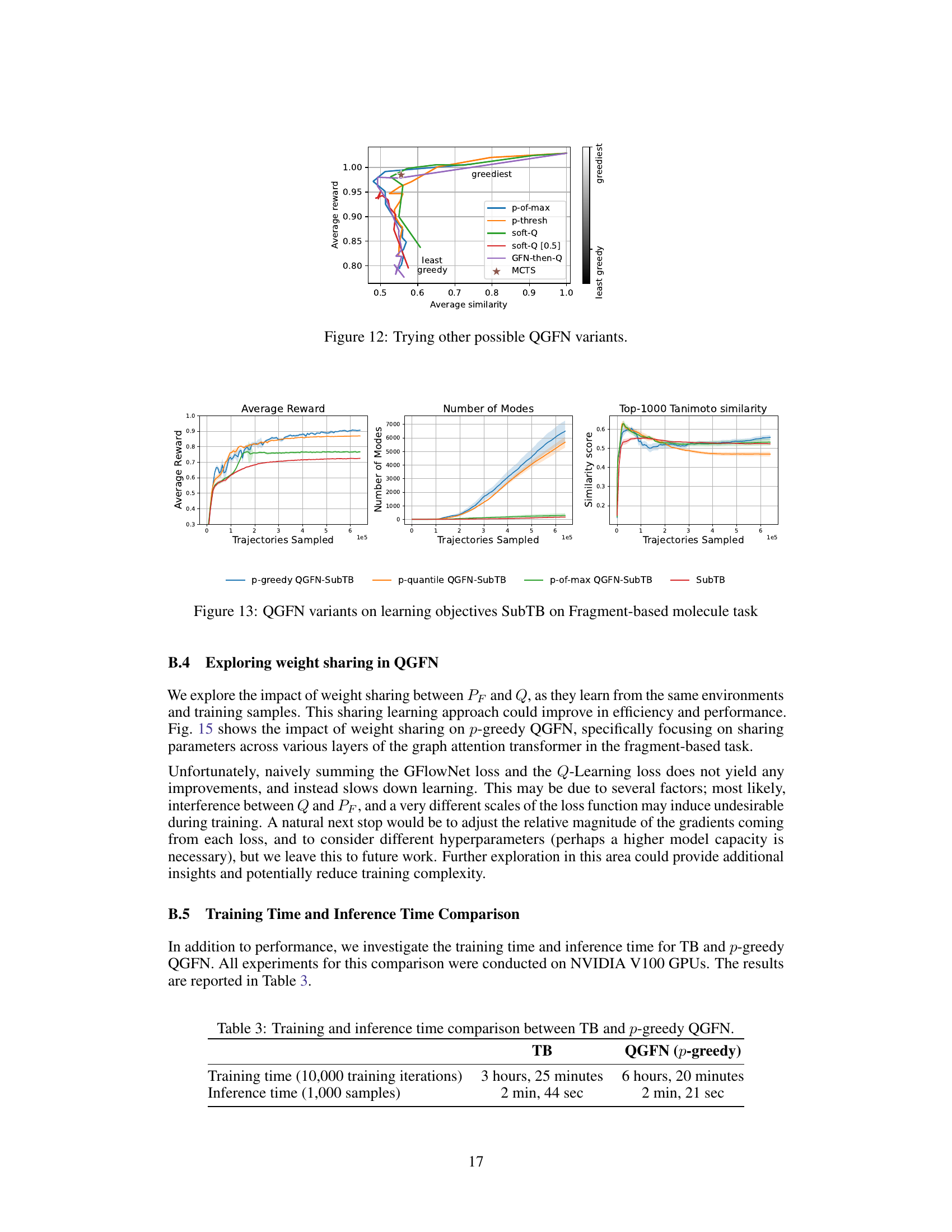
This figure displays the impact of changing the parameter ‘p’ during inference on the average reward and average similarity of generated samples in the fragment-based molecule generation task. The x-axis shows average similarity, while the y-axis presents average reward. Each line represents a different QGFN variant. The color gradient indicates how greedy the sampling policy is (from least greedy to greediest). As ‘p’ increases, the average reward generally increases while average similarity decreases, indicating a trade-off between reward and diversity. The MCTS method (marked by a star) shows high rewards but less diversity than other methods.
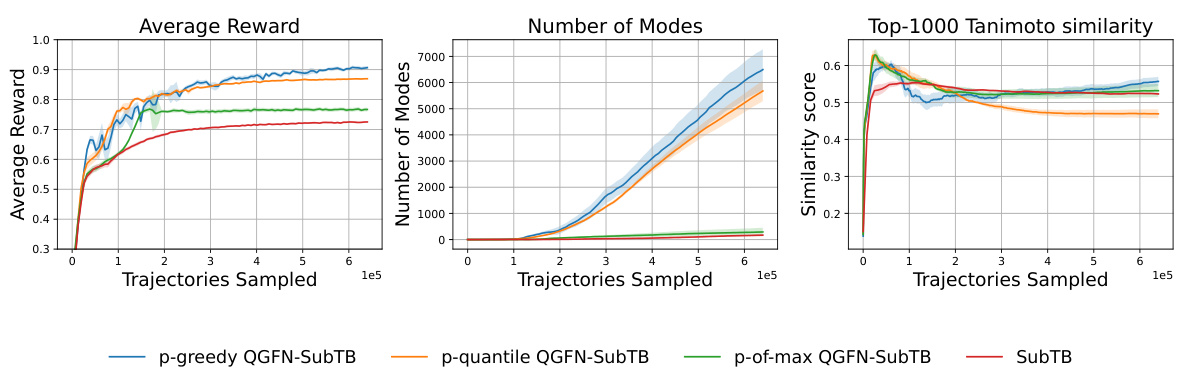
This figure compares the performance of three QGFN variants (p-greedy, p-quantile, and p-of-max) and the SubTB baseline on the fragment-based molecule generation task. The plots show the average reward, the number of unique modes discovered, and the average Tanimoto similarity score of the top 1000 molecules sampled over the course of training. The results demonstrate that the QGFN variants consistently outperform the SubTB baseline in terms of both average reward and the number of modes discovered.
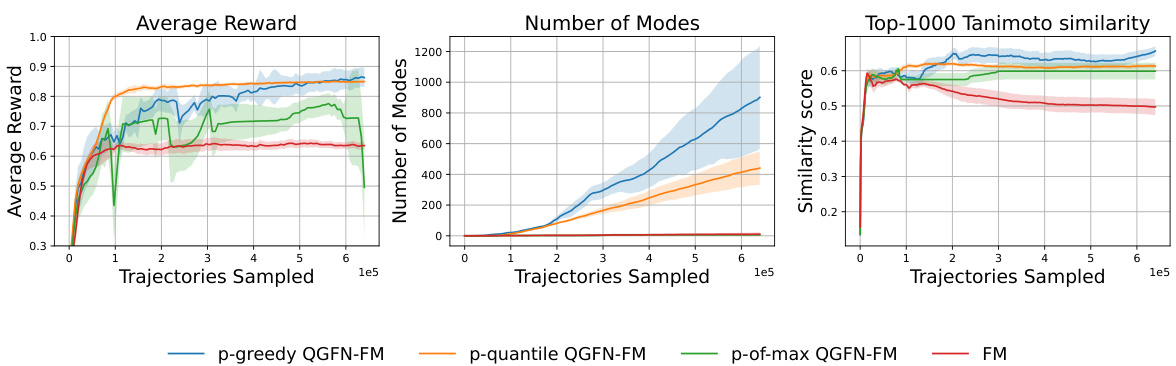
This figure presents the results of experiments comparing different variants of the QGFN algorithm (p-greedy QGFN-FM, p-quantile QGFN-FM, p-of-max QGFN-FM) against a baseline method (FM) on a fragment-based molecule generation task. Three plots are shown: Average Reward, Number of Modes, and Top-1000 Tanimoto Similarity. The x-axis represents the number of trajectories sampled, indicating progress during training. The y-axes show the respective metrics, Average Reward illustrating the average reward obtained, Number of Modes representing the number of unique molecular structures discovered, and Top-1000 Tanimoto Similarity indicating the average similarity of the top 1000 molecules, where lower values suggest greater diversity. The shaded areas represent standard error, and each line represents the average over multiple runs.
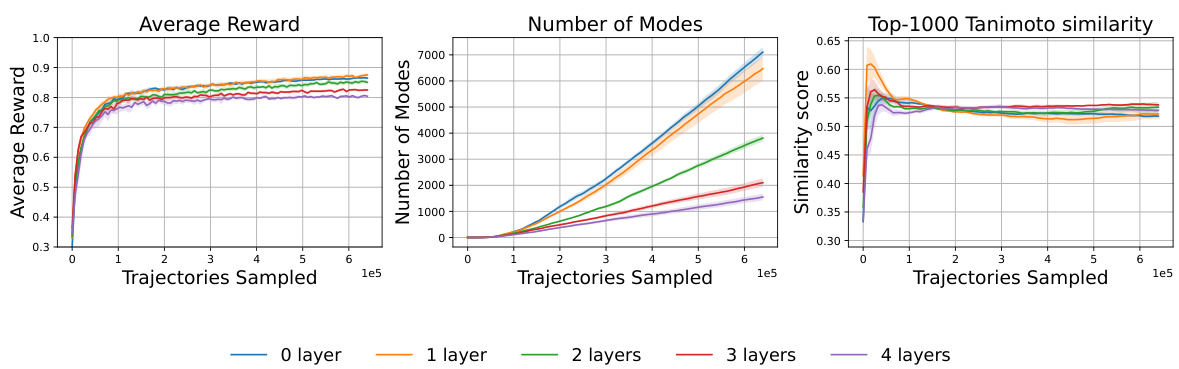
This figure illustrates the impact of weight sharing between the policy network (PF) and the action-value network (Q) in the p-greedy QGFN model, specifically focusing on different layers of the graph attention transformer. The results show the average reward, number of unique modes, and average pairwise Tanimoto similarity scores over the training trajectories for various layer sharing configurations (0, 1, 2, 3, and 4 layers). The experiment was conducted on the fragment-based molecule generation task. The plot shows that sharing weights does not always lead to improvements, potentially due to conflicts between gradients from different loss functions, or differences in scale.
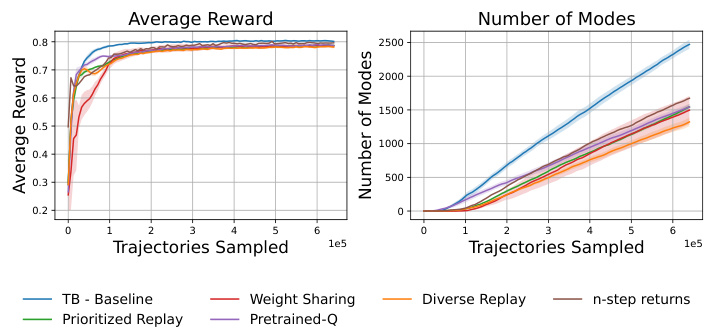
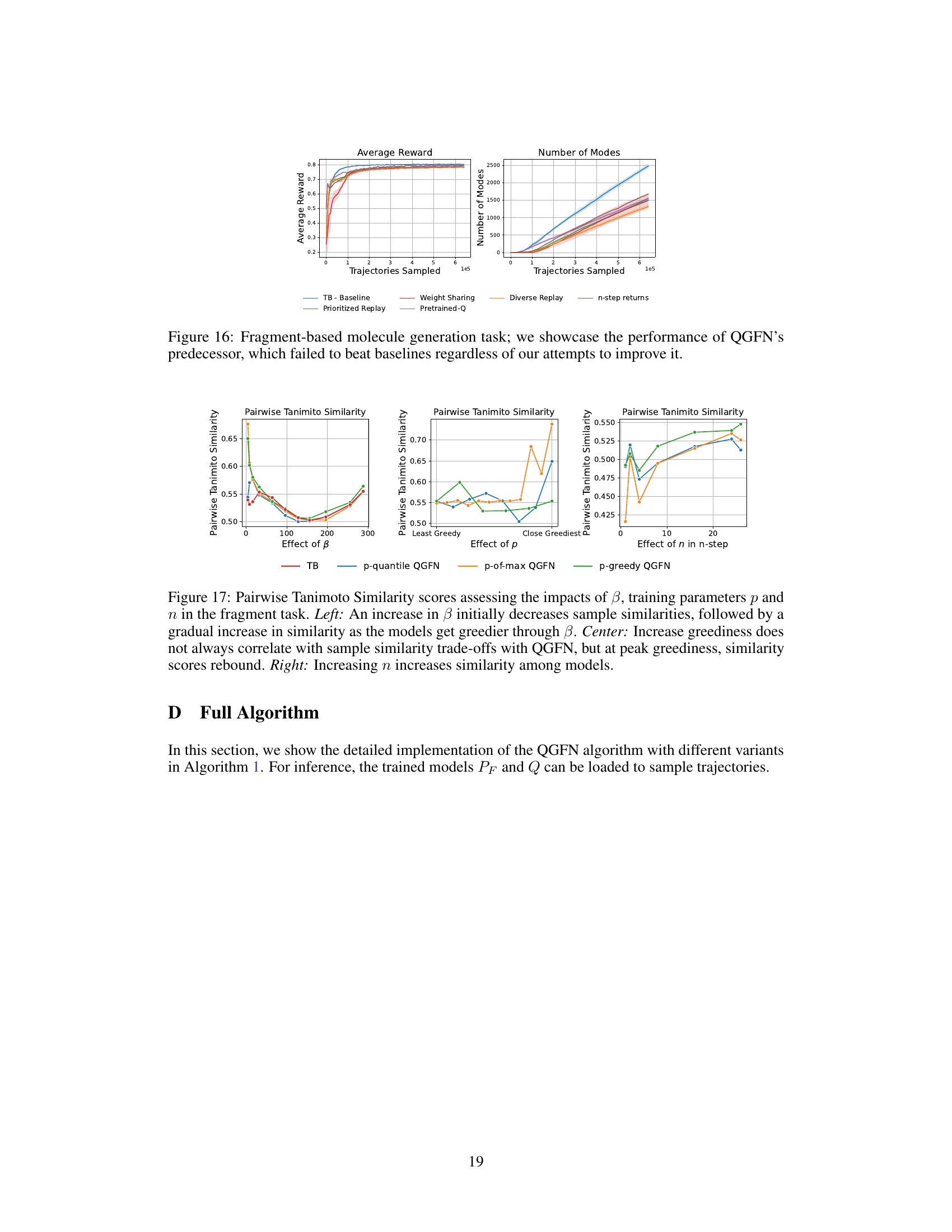
This figure displays the results of several approaches that were tried before developing QGFN, all of which failed to outperform baseline methods. The approaches shown include using a diverse-based replay buffer, an adaptive reward prioritized replay buffer, weight sharing between the GFN and DQN, using a pretrained Q-network to guide the selection of greedier actions, and simply using n-step returns. The results are presented in terms of average reward and the number of unique modes discovered across different methods. The figure demonstrates that none of these pre-QGFN approaches achieved better results than the simpler baselines, highlighting the significance of the QGFN approach.
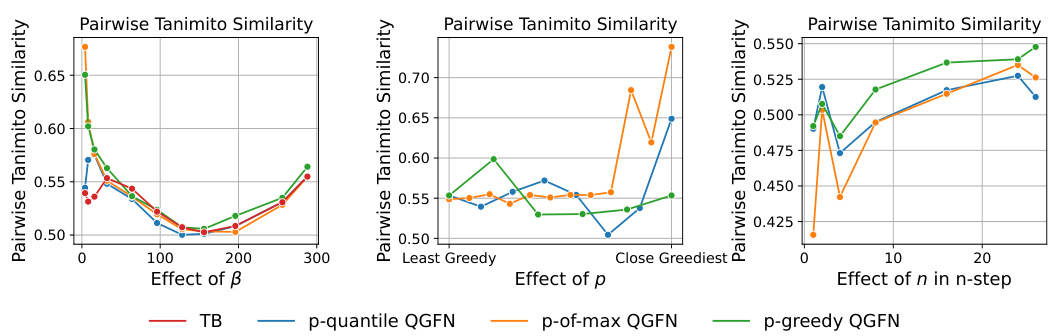
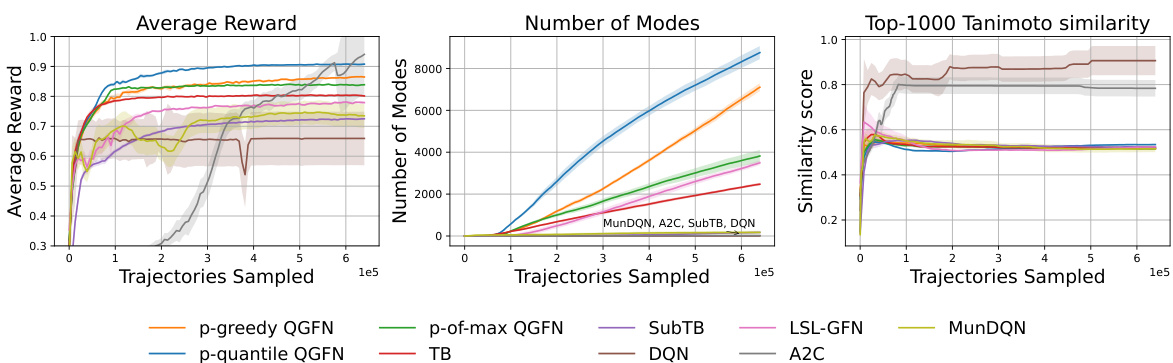
This figure shows the effect of hyperparameters β, p, and n on the pairwise Tanimoto similarity scores in the fragment-based molecule generation task. The left panel demonstrates that increasing β initially reduces similarity, but as the model becomes greedier, similarity increases again. The center panel illustrates that increasing the greediness parameter p doesn’t always negatively affect similarity, showing a complex relationship. The right panel reveals that increasing n (the number of bootstrapping steps in Q-learning) leads to higher similarity scores.
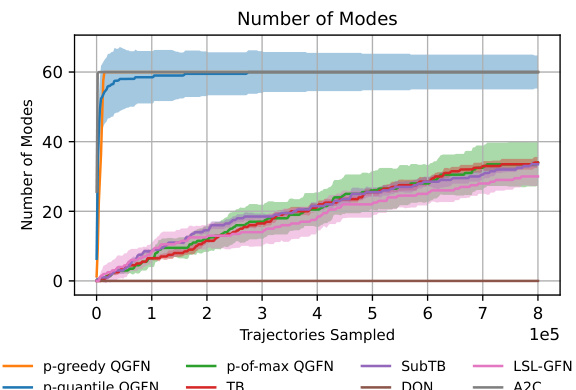
This figure displays the results of the fragment-based molecule generation task. The left panel shows the average reward across multiple training trajectories for various methods, illustrating how the proposed QGFN methods consistently achieve higher average rewards compared to baselines. The center panel compares the number of unique modes (high-reward, diverse molecules) discovered by each method, demonstrating the effectiveness of QGFNs in finding diverse high-reward molecules. The right panel presents the average pairwise Tanimoto similarity among the top 1000 molecules sampled, with lower values indicating higher diversity. The error bars represent the interquartile range across five independent experimental runs.
More on tables

This table presents the results of using a pre-trained Q-function (action-value) from a QGFN model during inference, but applied to independently trained baseline GFN models (Trajectory Balance and SubTrajectory Balance). It shows the average reward and diversity obtained for these models, illustrating how using the pre-trained Q-function can still improve performance on models not trained with Q. The table includes results for three different QGFN variants (p-greedy, p-of-max, p-quantile), demonstrating the effect of varying the greediness parameter.

This table presents a comparison of the reward and diversity achieved by different methods on the fragment-based molecule generation task. The metrics reported are the average reward and the average pairwise Tanimoto similarity (a measure of diversity) calculated from 1000 samples obtained after training. The methods compared include GFN-TB (Generative Flow Network with Trajectory Balance loss), GFN-SubTB (Generative Flow Network with Sub-Trajectory Balance loss), LSL-GFN (Logit Scaling for GFlowNets), and three variants of the proposed QGFN method (p-greedy, p-of-max, and p-quantile). The results demonstrate the improvement in reward achieved by the QGFN methods compared to baselines without sacrificing diversity. The table highlights the controllable greediness of the QGFN methods.
This table presents the average reward and diversity (measured by average pairwise Tanimoto similarity) of different methods on the fragment-based molecule generation task. The results are obtained at inference time after training the models. It compares the performance of several QGFN variants against baseline methods (GFN-TB, GFN-SubTB, LSL-GFN) to demonstrate the ability of QGFN to achieve higher rewards without sacrificing diversity.
This table shows the average reward and diversity (measured by average pairwise Tanimoto similarity) of different methods on the fragment-based molecule generation task after training. The methods compared include various GFN (Generative Flow Network) baselines and the proposed QGFN (Q-enhanced Generative Flow Network) variants. It highlights that QGFN methods generally achieve higher rewards without significantly sacrificing diversity compared to the baseline methods.
This table presents a comparison of the reward and diversity achieved by different methods on the fragment-based molecule generation task after training. The methods compared include GFN-TB, GFN-SubTB, LSL-GFN, and three variants of the proposed QGFN method (p-greedy, p-of-max, and p-quantile). The reward metric measures the average reward of the generated molecules, while the diversity metric reflects the average pairwise Tanimoto similarity, indicating the dissimilarity between generated molecules. Higher reward and lower similarity values are desired.
This table presents a comparison of the reward and diversity obtained by different methods after training on the fragment-based molecule generation task. The reward metric reflects the average reward of the generated molecules, while the diversity metric (similarity) measures the average pairwise similarity between molecules. Lower similarity indicates greater diversity. The results show the performance of various models, including GFN-TB, GFN-SubTB, LSL-GFN, and the three proposed QGFN variants (p-greedy, p-of-max, p-quantile). The comparison aims to demonstrate the effectiveness of QGFN in enhancing the generation of high-reward and diverse molecules.
This table presents the results of experiments on the fragment-based molecule task using independently trained baseline models with a pretrained Q-function for inference. It compares the performance of three QGFN variants (p-greedy, p-of-max, and p-quantile) against two baseline methods (TB and SubTB) in terms of reward and diversity. The p values used for each QGFN variant are specified in the caption.
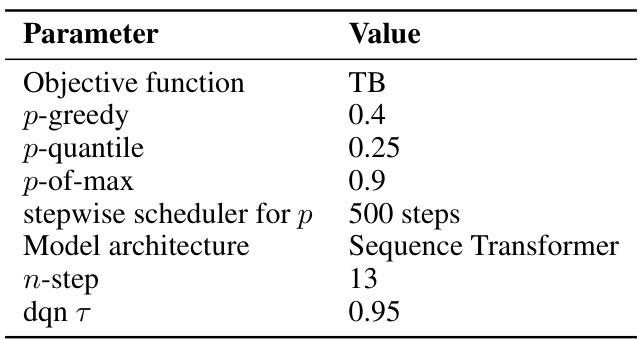
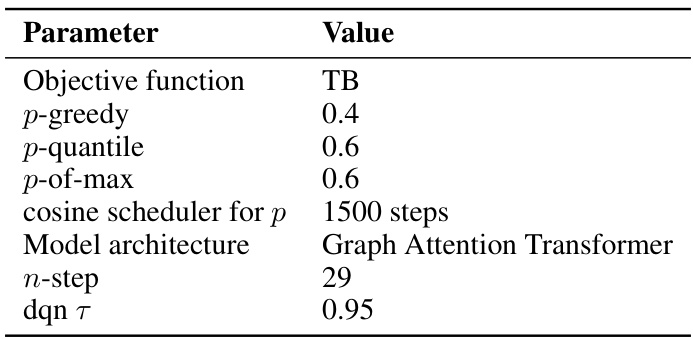
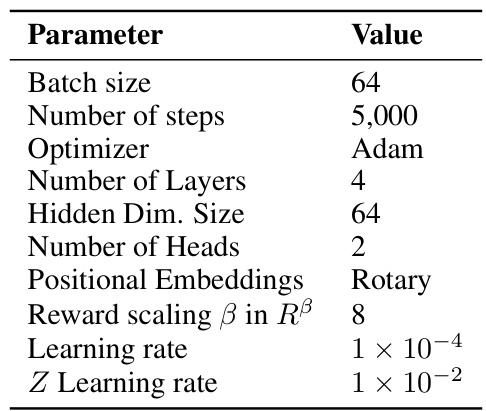
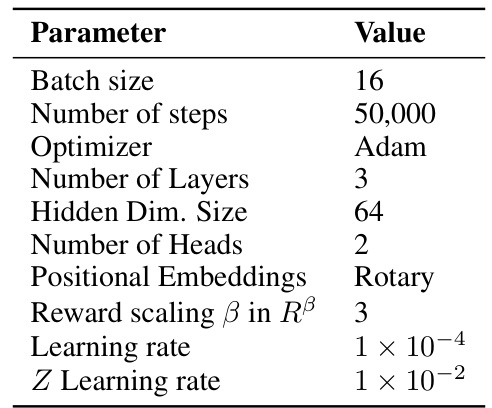
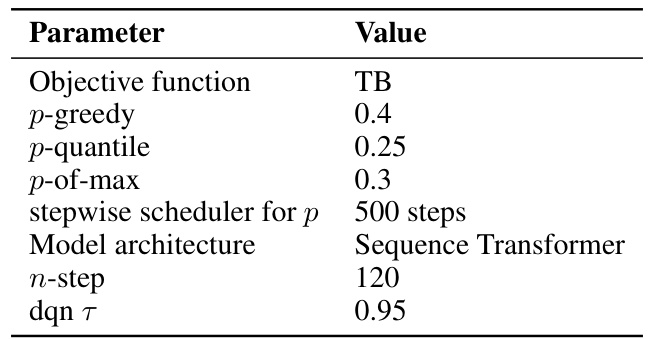
This table lists the hyperparameters used for the QGFN model in the RNA-binding task. It specifies the objective function used for training (TB), the values of the greediness parameter p for the three QGFN variants (p-greedy, p-quantile, p-of-max), the schedule for annealing the p parameter, the model architecture used (Sequence Transformer), the number of steps used for the n-step Q-learning method, and the temperature parameter τ for the DQN. These parameters were tuned to optimize performance on the RNA-binding task.
This table presents the average reward and diversity of different models on the fragment-based molecule generation task after training. It compares the performance of several methods, including GFN-TB, GFN-SubTB, LSL-GFN, and three variants of the proposed QGFN approach (p-greedy, p-of-max, and p-quantile). The reward metric is higher is better, and diversity (measured by average Tanimoto similarity) is lower is better. The results demonstrate the ability of QGFN to achieve higher rewards without sacrificing diversity compared to baseline methods.
This table presents the results of an experiment evaluating the performance of independently trained baseline models (TB and SubTB) when guided by a pre-trained Q-function during inference. Three variants of the QGFN approach (p-greedy, p-of-max, and p-quantile) are compared against the baselines. The table shows the average reward and diversity achieved by each method. The p-values used in the QGFN variants are specified to provide context. This experiment demonstrates that using a pre-trained Q-function can enhance the performance of independently trained models even on tasks where those models performed poorly during training.
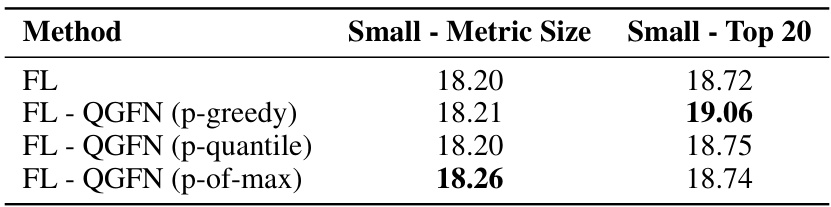
This table presents a comparison of the reward and diversity achieved by different methods on the fragment-based molecule generation task, specifically focusing on results obtained during the inference phase after model training. The methods compared include baseline GFN approaches (GFN-TB and GFN-SubTB), LSL-GFN (a method that controls greediness through temperature conditioning), and three variants of the proposed QGFN approach (p-greedy, p-of-max, and p-quantile). For each method, the average reward and average pairwise Tanimoto similarity (a measure of diversity) across 1000 samples are reported, along with standard errors.
Full paper#