↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world goal-oriented problems are contextual, where an agent’s objective is to reach a goal within a context. Solving these problems with offline datasets presents unique challenges, as rewards are sparse and relationships between contexts and goals are not always clear. Existing methods face limitations in handling these complexities, often requiring additional approximations or relying on specific assumptions.
This paper introduces CODA, a novel data augmentation technique for offline reinforcement learning. CODA cleverly constructs an equivalent action-augmented MDP, enabling the creation of a fully-labeled dataset from unlabeled trajectories and context-goal pairs. By leveraging the structure of contextual goal-oriented problems, CODA circumvents the challenges of sparse rewards and unknown context-goal relationships. The paper provides a theoretical analysis demonstrating CODA’s capability to solve these problems and showcases its effectiveness through empirical results, outperforming various baseline methods across different context-goal relationships. CODA offers a promising and efficient approach for tackling real-world contextual goal-oriented problems with limited labeled data.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel method, CODA, to solve contextual goal-oriented problems using only offline datasets. This is a significant contribution because many real-world applications have limited access to labeled data, and this work provides a viable solution to leverage existing data effectively. The theoretical analysis and experimental results demonstrate the effectiveness of CODA and its potential to advance research in offline reinforcement learning and related fields. The new avenues opened by CODA’s success in handling the missing-label problem further enhance its value for researchers in various domains.
Visual Insights#
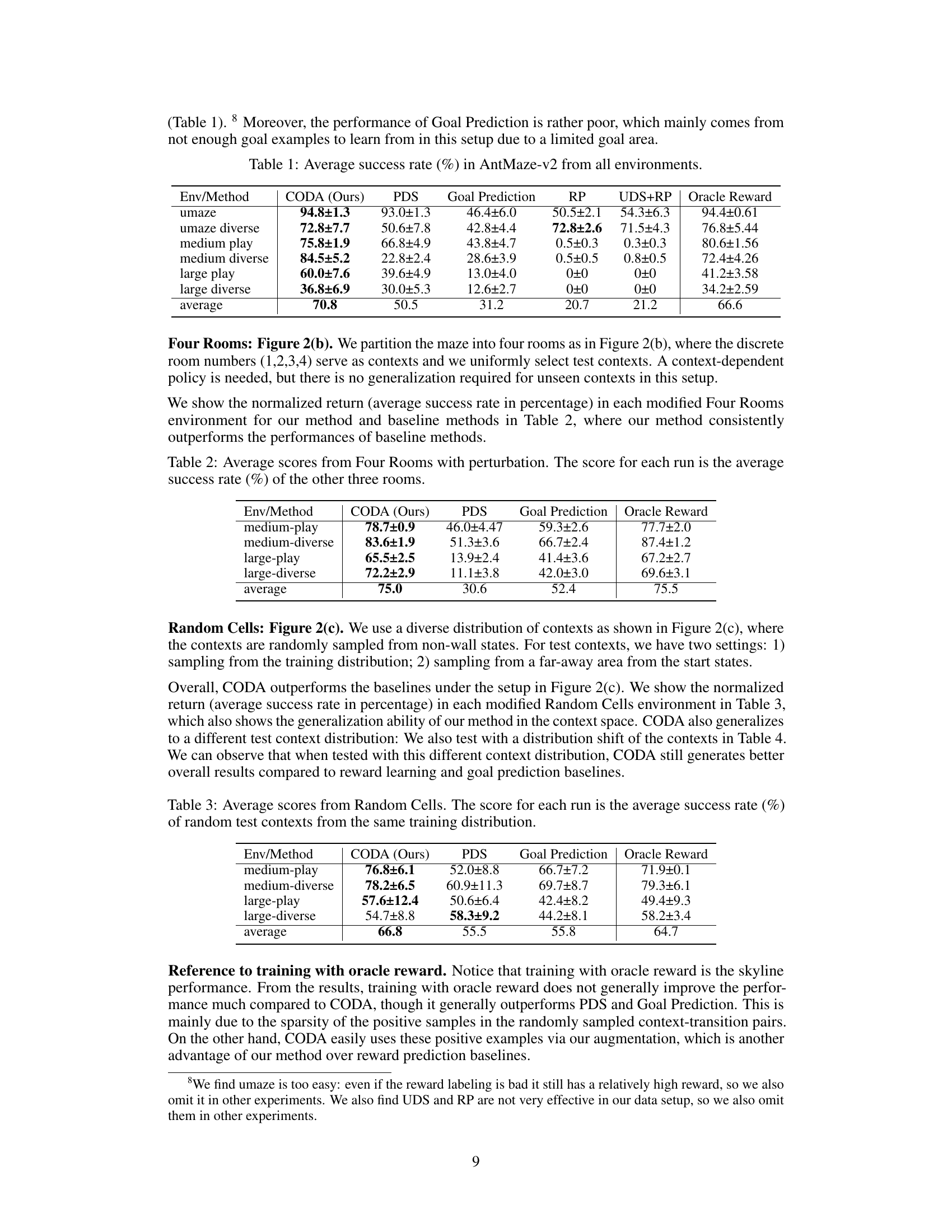
This figure illustrates the core idea of the CODA method. CODA augments the original Markov Decision Process (MDP) by adding fictitious transitions. These transitions originate from goal examples in the context-goal dataset and lead to a terminal state, with a reward of 1. The fictitious actions are associated with the given context. This augmentation allows the supervised learning signal from the context-goal pairs to propagate through the Bellman equation to the unlabeled transitions from the dynamics dataset, effectively creating a fully labeled dataset for offline reinforcement learning.
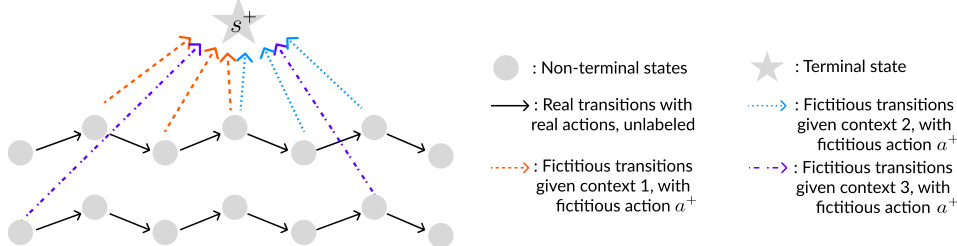
This table presents the average success rates achieved by different methods (CODA, PDS, Goal Prediction, RP, UDS+RP, and Oracle Reward) across six different AntMaze-v2 environments. Each environment varies in complexity (umaze, umaze diverse, medium play, medium diverse, large play, large diverse). The success rate is a measure of how often the agent successfully reached the goal. The table shows CODA generally performs better than reward-learning and goal prediction baselines, particularly in more complex environments.
In-depth insights#
Offline CGO Solver#
An offline contextual goal-oriented (CGO) solver is a system designed to learn optimal policies for CGO problems using only pre-collected data, without any interaction with the real environment. This is crucial because online data collection can be expensive, time-consuming, or even impossible in many real-world applications. A key challenge in offline CGO solvers is the sparsity of reward signals and the complexity of context-goal relationships. CODA (Contextual goal-Oriented Data Augmentation) is a novel method that addresses this challenge by cleverly creating a fully labeled dataset from unlabeled trajectory and context-goal data. This approach avoids the need for reward modeling or dealing with missing labels, which are major hurdles for other offline reinforcement learning methods. The method’s effectiveness is demonstrated empirically across varied CGO problem complexities, showcasing its capability to outperform existing baselines. The theoretical analysis further validates CODA’s capability to solve CGO problems with only positive data, implying that learning is feasible even without negative examples. This property significantly enhances the applicability of offline CGO solvers in situations where collecting negative data is difficult.
CODA Augmentation#
The proposed CODA (Contextual Goal-Oriented Data Augmentation) method is a novel data augmentation technique designed to address the challenges of offline contextual goal-oriented reinforcement learning. CODA cleverly augments the offline dataset by creating fictitious transitions from goal examples to a terminal state, effectively turning a partially labeled dataset into a fully labeled one. This approach leverages the structure inherent in CGO problems—where transition dynamics are independent of contexts—by creating fictitious transitions under training contexts. The key contribution is the theoretical guarantee that this augmentation does not introduce additional approximation error, ensuring the learned policy remains optimal within the framework of an action-augmented Markov Decision Process. This innovative method avoids the drawbacks of simpler techniques, such as goal prediction and reward modeling, which often rely on potentially inaccurate approximations or insufficient data. CODA’s effectiveness is demonstrated empirically across various context-goal relationships, showcasing its superior performance over other baselines. The core idea of converting a sparsely rewarded problem into a fully labeled one is highly significant, allowing the direct application of standard offline reinforcement learning algorithms. This augmentation is theoretically proven to be sound, effectively bridging the gap between existing offline RL methods and the specific needs of contextual goal-oriented tasks.
Positive Data Learn#
The concept of “Positive Data Learn” in machine learning focuses on training models using only positive examples, omitting negative data. This approach presents several key advantages. Firstly, it can significantly reduce the effort and cost associated with data labeling, as acquiring negative examples is often more time-consuming and expensive. This is particularly beneficial in domains with imbalanced class distributions, where positive data might be abundant while negative examples are rare. Secondly, it offers robustness to noisy or ambiguous negative data, which can lead to inaccurate or biased models. Positive data learning is particularly useful when dealing with complex or high-dimensional data, where it can be challenging to define negative examples effectively. However, this method also presents limitations. Models trained solely on positive data might lack the capacity to generalize well to unseen data, which is crucial for successful deployment. This limitation stems from the lack of information about the characteristics of the negative class. It is crucial to carefully assess the trade-offs between the cost-effectiveness of the positive data learning approach and the potential impact on the generalization of the model.
Empirical Analysis#
An empirical analysis section in a research paper would typically present the results of experiments designed to test the paper’s hypotheses or claims. A strong empirical analysis would begin by clearly describing the experimental setup, including the datasets used, the metrics employed, and any preprocessing steps. It’s crucial to justify the choice of datasets and metrics, showing they are appropriate for addressing the research questions. The analysis should then present the results in a clear and organized manner, using tables, figures, and statistical tests where appropriate. Statistical significance of the findings must be thoroughly discussed, accounting for potential biases or limitations. A thoughtful analysis would not only report the results but also interpret them in the context of the paper’s theoretical contributions and prior work. Finally, a robust empirical analysis would acknowledge any limitations of the study and suggest directions for future research. The overall goal is to present convincing evidence supporting the paper’s claims while maintaining transparency and rigor.
Future CGO Research#
Future research in Contextual Goal-Oriented (CGO) problems should prioritize addressing limitations in current methods. Scalability to high-dimensional state and action spaces is crucial for real-world applications, and requires exploring efficient representation learning techniques and potentially leveraging pre-trained models. The current theoretical analysis mainly focuses on the positive data; therefore, understanding the role of negative data or developing robust methods that effectively handle uncertainty with limited data is important. Improving generalization capabilities across diverse contexts and goal relationships is a key area, necessitating research into more sophisticated contextual representations and robust reward shaping techniques. Benchmarking efforts are also needed for consistent evaluation of CGO algorithms, including the introduction of standardized datasets covering a wider range of CGO complexities. Finally, exploration into novel reward functions that explicitly incorporate the context into the reward signal is likely to improve learning efficiency and robustness.
More visual insights#
More on figures
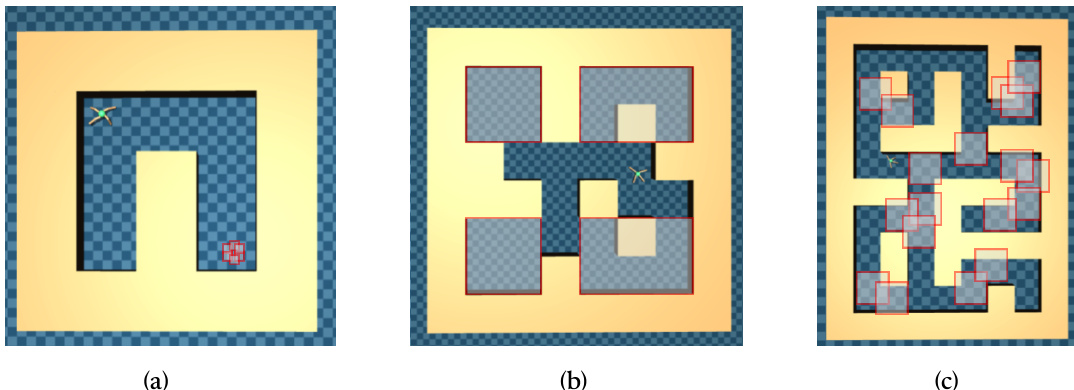
This figure illustrates three levels of complexity in the context-goal relationship in contextual goal-oriented (CGO) problems. (a) shows a simple scenario where contexts and goals are very similar, making it solvable by a context-agnostic policy. (b) demonstrates a scenario with finite contexts, each mapping to distinct goal sets, necessitating context-dependent policies. Finally, (c) depicts the most complex scenario with continuous and infinite contexts and a non-trivial mapping between contexts and goals, showcasing the full complexity of CGO problems.
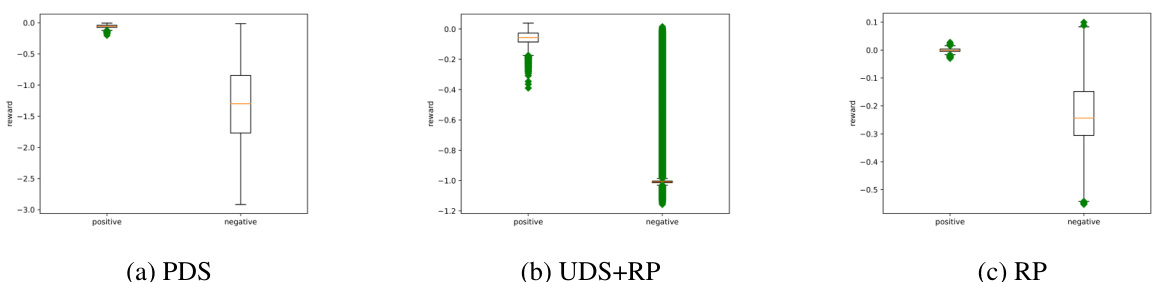
This figure shows the reward model evaluation for the large-diverse dataset in the original AntMaze environment. The box plots display the distribution of predicted rewards for both positive (context-goal pairs) and negative (context-non-goal pairs) samples. Green dots represent outliers, which are data points that fall significantly outside the typical range of values in the dataset. The figure visually compares the performance of three reward learning models: PDS, UDS+RP, and RP in distinguishing positive from negative samples.
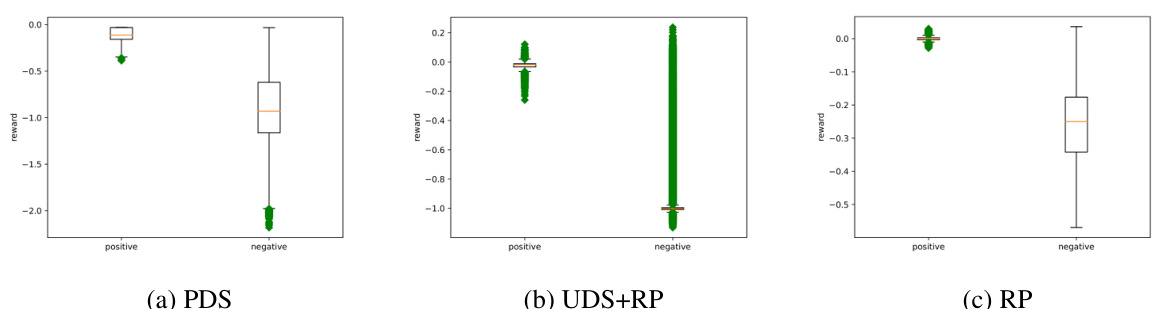
The figure shows box plots visualizing the reward distributions obtained from evaluating the reward models (PDS, UDS+RP, and RP) on both positive and negative datasets within the large-diverse environment of original AntMaze. It demonstrates that PDS performs better at separating positive and negative samples than the other two models, although all three struggle to fully separate the distributions.
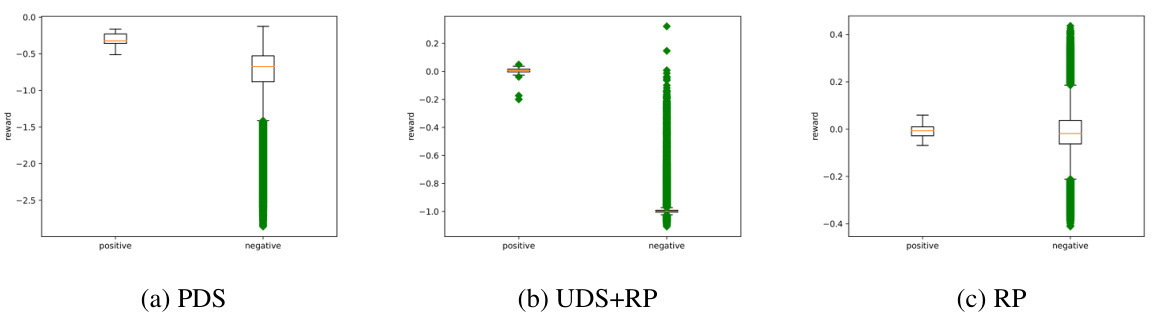
The box plot shows the distribution of predicted rewards from three different reward models (PDS, UDS+RP, and RP) on positive and negative samples for the large-diverse dataset in the original AntMaze environment. The positive samples are context-goal pairs, and negative samples are randomly selected from the context and non-goal states in the dataset. The plots illustrate the performance of each reward model in separating positive and negative samples. Green dots indicate outliers.

This figure illustrates three levels of context-goal relationships with increasing complexity. The first shows very similar contexts and goal sets, meaning a context-agnostic policy may suffice. The second shows finite contexts mapping to distinct goal sets, requiring context-dependent policies. The third depicts continuous and infinite contexts with a complex, neither one-to-many nor many-to-one, context-goal mapping, representing the full complexity of the CGO problem.

This figure shows the box plots of reward model evaluation for the large-diverse dataset in the original AntMaze environment. The box plots show the distribution of the predicted reward for both positive and negative datasets. Green dots represent outliers.
More on tables
This table presents the average success rates achieved by different methods in a modified Four Rooms environment. The environment was modified by introducing perturbations, making it more challenging. The score for each run represents the average success rate across three out of the four rooms, excluding the room where the run started.

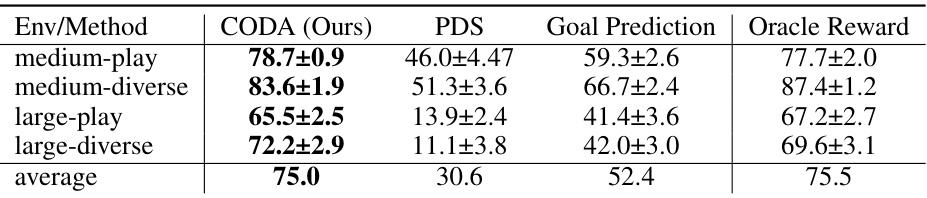
This table presents the average success rates achieved by different methods (CODA, PDS, Goal Prediction, and Oracle Reward) in the Random Cells environment. The success rate is calculated as the average percentage of successful goal-reaching episodes across multiple trials in each environment. The data is broken down by the difficulty of the Random Cells environment (medium vs. large) and whether the dataset has diverse context-goal relationships or not (diverse vs. play). The table shows that CODA generally achieves higher average success rates than other methods.
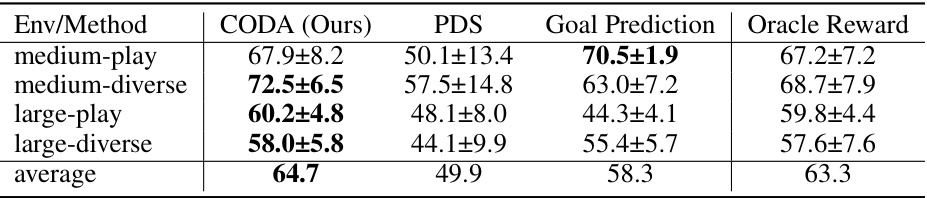
This table presents the average success rates of different methods (CODA, PDS, Goal Prediction, and Oracle Reward) in the Random Cells environment when there is a distribution shift between the training and testing contexts. The results show the performance of each method across four different environments (medium-play, medium-diverse, large-play, large-diverse) and the average performance across all four environments. The standard deviation is also included for each entry.

This table presents the average success rates of CODA on the AntMaze-v2 environment with different sampling ratios from the context-goal dataset. The success rate is a measure of how often the algorithm successfully reaches the goal. The table shows results for different environments (umaze, umaze diverse, etc.) and different sampling ratios of the context-goal pairs (0.1, 0.3, 0.5, 0.7, 0.9). The results demonstrate the robustness of CODA across various sampling ratios.
Full paper#