QBB: Quantization with Binary Bases for LLMs

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on large language model optimization and deployment. It presents a novel quantization method that significantly improves efficiency and reduces computational costs, opening new avenues for research on low-bit quantization techniques and hardware-aware model design. The method’s data-free nature makes it particularly valuable and broadly applicable.

Visual Insights

#

This figure illustrates the process of initializing binary weights. Starting with the original weight matrix W, the method iteratively creates N binary matrices (B1 to BN) and their corresponding scaling vectors (α1 to αN). Each binary matrix approximates the residual error from the previous approximation. The first binary matrix and scaling vector are calculated analytically using equation 2, and subsequent ones are calculated using equation 3. This analytical initialization serves as the foundation for the subsequent iterative optimization.

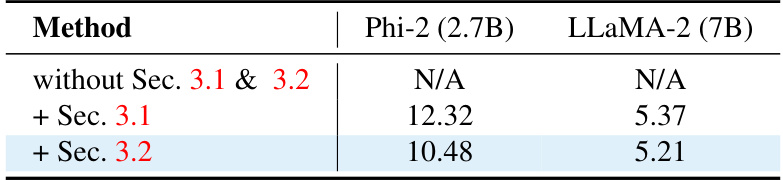
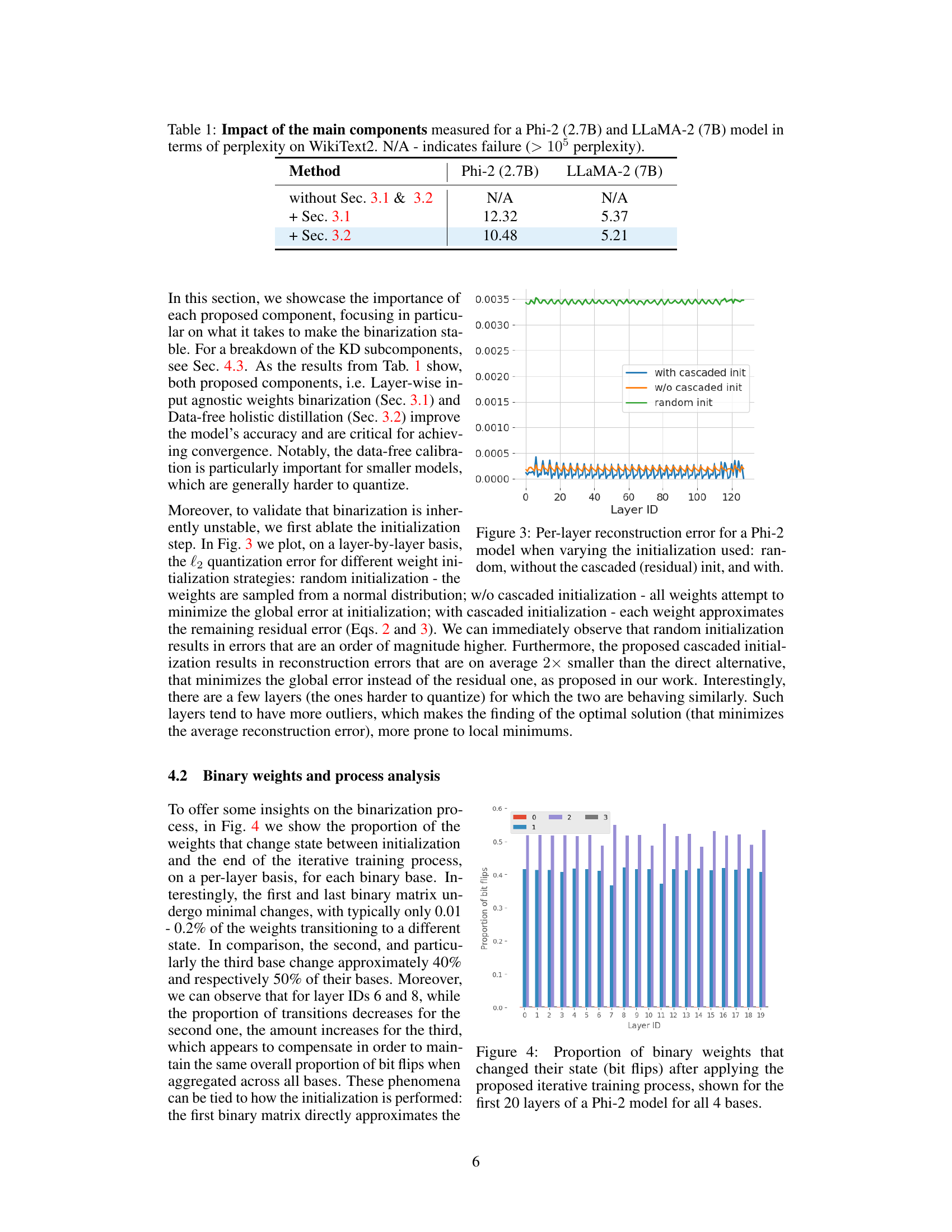
This table shows the impact of the proposed method’s components on the perplexity scores of Phi-2 (2.7B) and LLaMA-2 (7B) models. It compares the perplexity when neither data-free holistic distillation nor layer-wise input-agnostic weight binarization is used, then with just layer-wise input-agnostic weight binarization, and finally with both techniques. The results demonstrate the importance of both proposed methods for achieving good model performance, especially for smaller models.

In-depth insights

#

Binary Weight Init

#

The effectiveness of binarized neural networks hinges critically on the initialization strategy for binary weights. Suboptimal initialization can lead to severe performance degradation, hindering the advantages of reduced computational cost. A well-designed initialization method should aim to preserve essential information from the original full-precision weights while ensuring that the binarized weights facilitate effective training. Approaches may involve analytical methods to directly map full-precision values to their binary equivalents or iterative processes that refine the binary weights during training. The choice of initialization directly impacts the convergence speed and final accuracy of the binarized network. Consequently, research in this area focuses on developing sophisticated methods that balance accuracy preservation with computational efficiency, adapting to various network architectures and datasets. Careful consideration of the trade-off between initial accuracy and trainability is paramount in achieving effective binarization.

Iterative Refinement

#

The concept of “Iterative Refinement” in a research paper context usually implies a process of improving a model, algorithm, or result through repeated cycles of modification and evaluation. Each iteration builds upon the previous one, incorporating feedback from analysis and experimentation to address shortcomings or limitations. This approach is particularly valuable when dealing with complex problems where an optimal solution is hard to find directly. Iterative refinement allows for a gradual approach, starting with a simpler or approximate solution and progressively enhancing its accuracy, efficiency, or other desired properties. The process often involves defining specific metrics to track progress, identifying bottlenecks or areas for improvement, and making targeted adjustments in each iteration. The loop continues until a satisfactory level of performance or a predetermined stopping criterion is met. Careful monitoring and evaluation at each step are crucial for guiding the refinement process and ensuring that improvements are meaningful and consistent with overall research goals. The iterative nature lends itself to both theoretical and experimental settings, providing opportunities for continuous validation and adaptation. This methodology often yields a more robust and refined end-product compared to approaches attempting to arrive at the best solution immediately.

Data-Free Tuning

#

Data-free tuning presents a compelling paradigm shift in the machine learning landscape, particularly for large language models (LLMs). Traditional tuning methods rely heavily on large, labeled datasets, which can be expensive, time-consuming, and sometimes even raise privacy concerns. Data-free techniques, however, leverage the model’s inherent capabilities to refine its parameters without needing external data. This approach has significant implications for deployment efficiency, as it bypasses the need for extensive datasets during model refinement. The core idea often involves using internally generated data or utilizing knowledge distillation from a pre-trained model, allowing for efficient adaptation to specific tasks or domains. While data-free methods are promising, it is essential to address potential limitations such as overfitting to the model’s internal representations and a potential reduction in the generalizability of the tuned model compared to data-driven approaches. Future research should focus on developing methods that enhance the robustness and generalizability of data-free tuning, while also exploring new ways to leverage the model’s internal knowledge for more effective parameter adaptation.

Efficiency Analysis

#

An efficiency analysis of a novel quantization method for LLMs would ideally explore several key aspects. First, a comparison of the computational cost (e.g., FLOPs) between the proposed method and existing state-of-the-art techniques is crucial. This would likely involve analyzing the number of multiplications and additions performed per inference step, noting the significant reduction achieved by replacing multiplications with summations. Memory usage is another important factor; the analysis should compare the memory footprint of the quantized model versus the original model and existing methods. Quantization error introduced during the process also needs detailed analysis, perhaps by comparing the perplexity scores or other relevant metrics on benchmark datasets. Finally, the analysis must consider hardware-specific efficiency: measuring inference speed and energy consumption on various hardware platforms such as GPUs and specialized AI accelerators will provide a more complete picture. The analysis must carefully consider the trade-offs between speed, accuracy, and memory to arrive at a comprehensive evaluation.

Future Directions

#

Future research could explore several promising avenues. Extending QBB to other quantization levels beyond binarization, such as ternary or quaternary, could offer a balance between compression and computational efficiency. Investigating alternative optimization strategies for the binary matrices and scaling vectors, potentially incorporating techniques beyond gradient descent, might lead to faster convergence and improved accuracy. Exploring different architectures and model types beyond LLMs to assess QBB’s generalizability and effectiveness is crucial. Finally, addressing the potential limitations of the data-free holistic binarization, such as the reliance on synthetic data, warrants further investigation. A deeper analysis of the impact of scaling vectors, and their optimization strategies, could significantly enhance this method’s applicability and robustness.

More visual insights

#

More on figures

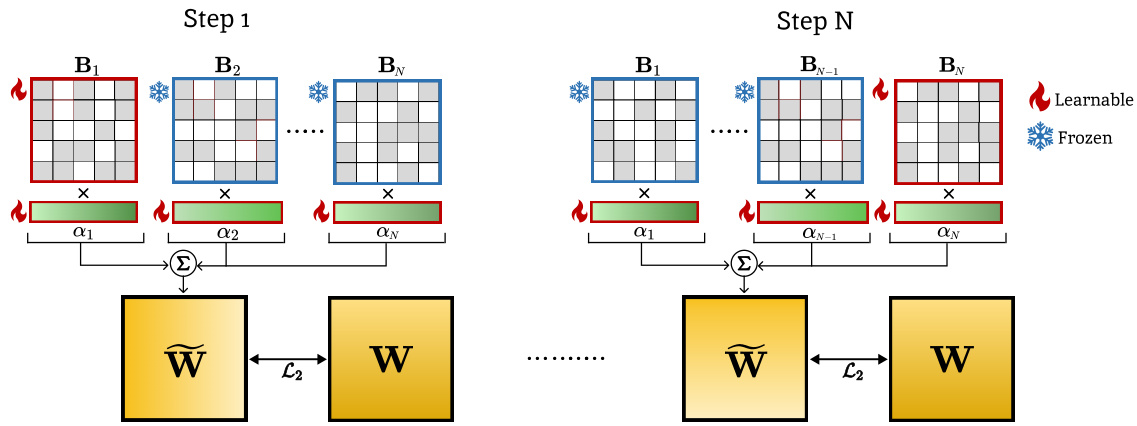
This figure illustrates the iterative process of weights binarization. Starting with weights initialized analytically (as in Figure 1), the algorithm iteratively refines the approximation of the original weights using multiple binary matrices (Bi) and scaling vectors (αi). In each step, only one binary matrix is updated while minimizing the L2 distance between the approximation and the original weights. All scaling vectors are updated in every step.

This figure compares the per-layer reconstruction error of a Phi-2 model under three different weight initialization strategies: random initialization, initialization without the cascaded (residual) method, and initialization with the cascaded method. The cascaded initialization method, a key component of the proposed QBB approach, shows significantly lower errors, demonstrating its effectiveness in minimizing the quantization error for each layer.

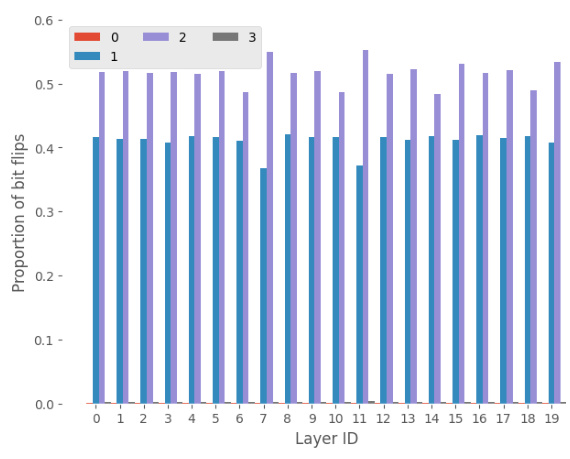
This figure visualizes the changes in binary weights during the iterative training process of the proposed quantization method. It shows, for each of the four binary bases used in approximating the weight matrix, the proportion of weights that change their value (+1 to -1 or vice versa) across 20 layers of a Phi-2 language model. The figure helps in understanding how different bases are modified to obtain better accuracy and the impact of the iterative approach on the weight adjustments across different layers of the model.

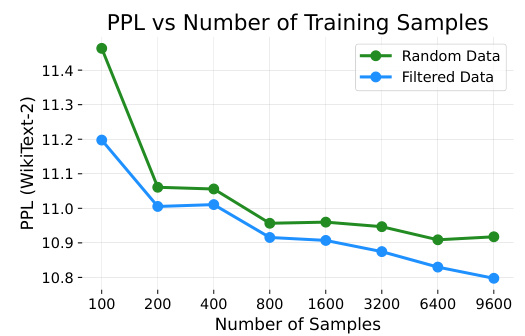
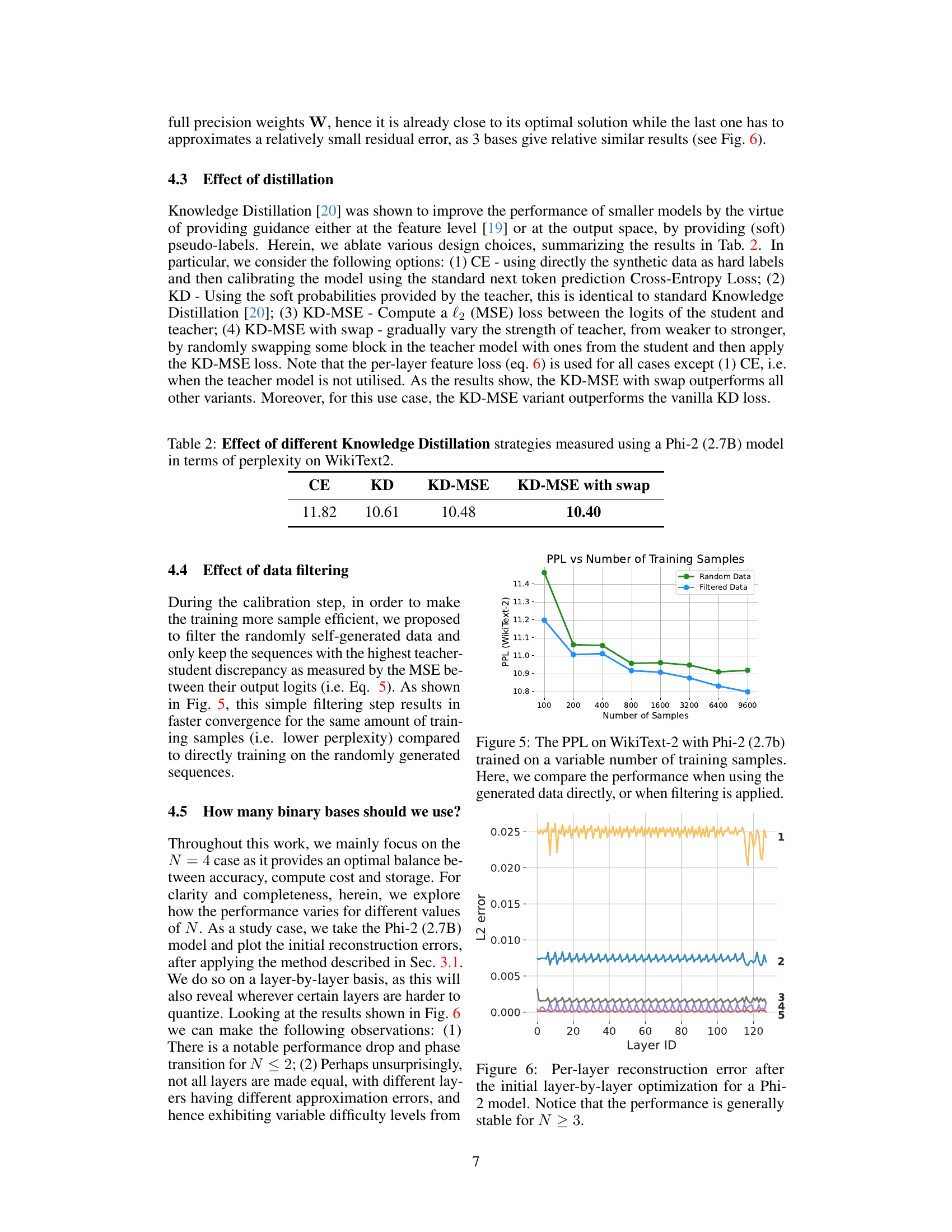
This figure shows the perplexity (PPL) on the WikiText-2 benchmark for a Phi-2 (2.7B) model trained using different numbers of training samples. Two training strategies are compared: one using randomly generated data and another using filtered data (only keeping sequences with high teacher-student discrepancy). The filtered data approach leads to faster convergence and lower perplexity for the same number of samples, demonstrating its efficiency.

This figure shows the L2 error (reconstruction error) for each layer of a Phi-2 model after the initial layer-by-layer optimization. The x-axis represents the layer ID, and the y-axis shows the L2 error. Multiple lines represent the error for different numbers of binary bases (N) used in the approximation. The figure demonstrates that the reconstruction error is generally stable and low when using 3 or more binary bases (N≥3), indicating that the proposed method effectively approximates the weights with the selected number of bases.

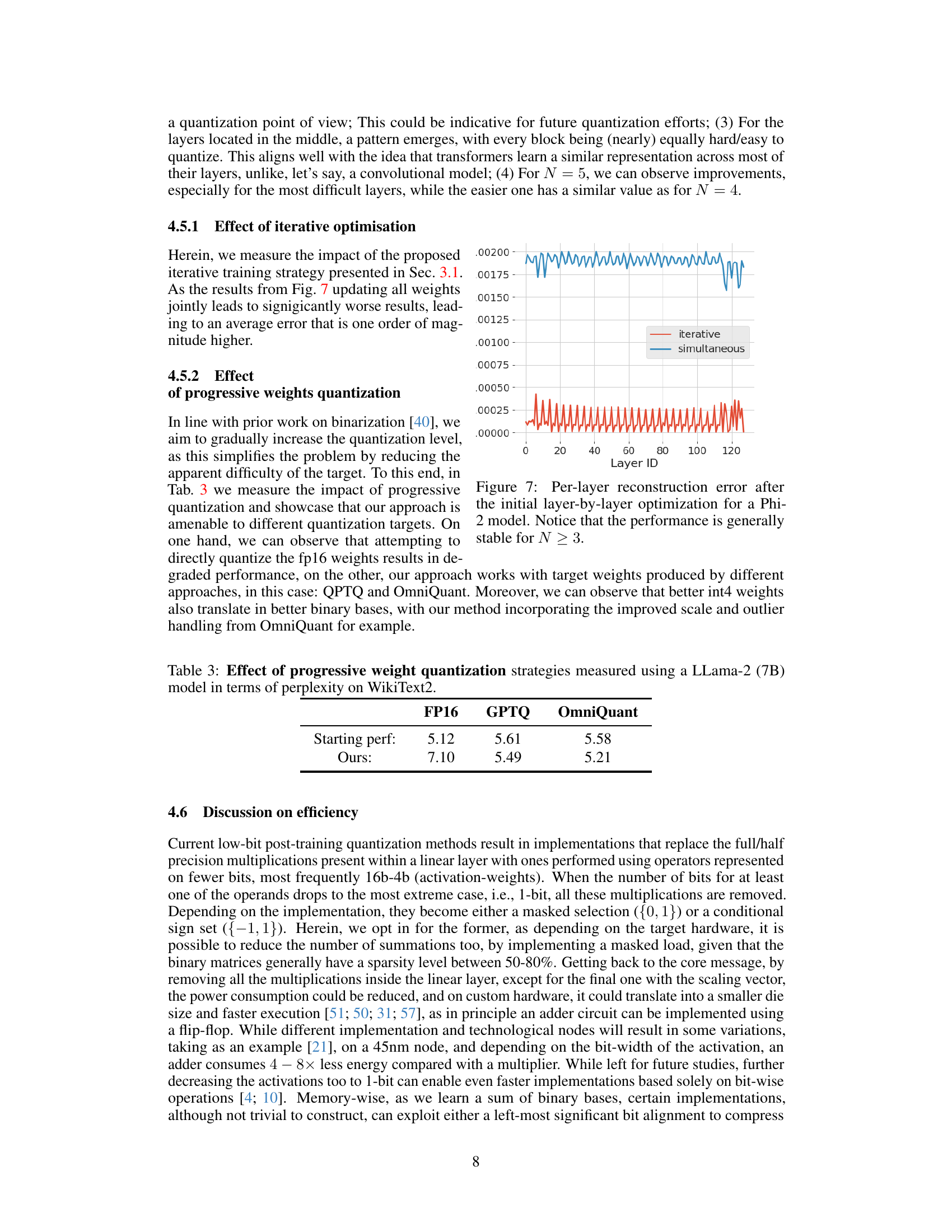
This figure compares the per-layer reconstruction error achieved by two different optimization strategies: iterative and simultaneous. The iterative approach, which updates binary weights one-by-one, shows significantly lower errors than the simultaneous update method. The results indicate that the proposed iterative strategy is more stable and effective for optimizing binary weights, particularly important in layers that are challenging to quantize. This figure supports the claim that the iterative approach improves the overall binarization process and is especially beneficial in handling the quantization challenges present in harder-to-quantize layers.

More on tables

This table presents the perplexity scores on the WikiText2 benchmark for a Phi-2 (2.7B) model using different knowledge distillation (KD) strategies. The strategies compared are: CE (Cross-Entropy loss using hard labels), KD (standard KD with soft labels), KD-MSE (MSE loss between student and teacher logits), and KD-MSE with swap (KD-MSE with teacher blocks gradually swapped with student blocks). The results show the impact of these strategies on the model’s performance, highlighting the effectiveness of the KD-MSE with swap approach.

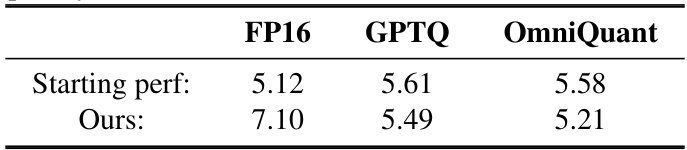
This table demonstrates the impact of using different quantization methods as a starting point for the proposed binary quantization approach. It compares the perplexity scores achieved on the WikiText2 benchmark when starting from full precision (FP16), GPTQ quantized weights, and OmniQuant quantized weights. The results highlight that using higher-quality quantized weights as input to the proposed method leads to better final performance.

This table presents the results of different weight-only quantization methods on LLaMA and LLaMA-2 models, measured by their perplexity scores on the WikiText2 benchmark. The methods compared include RTN (Round to Nearest), GPTQ, AWQ, OmniQuant, and QuIP#, each with different quantization bit-widths (W4A16, W4A16g128, W3A16, W3A16g128) and grouping strategies. The table shows the perplexity scores achieved by each method across various model sizes, providing a quantitative comparison of their performance.

Full paper

#