Why the Metric Backbone Preserves Community Structure

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on graph sparsification and community detection. It introduces a novel approach using the metric backbone, demonstrating its efficiency and robustness in preserving community structure, which has significant implications for various applications dealing with large and complex networks. The theoretical analysis and empirical validation provide valuable insights into community structure preservation during network sparsification, while the application to q-NN graph construction offers a practical solution for improving data analysis in machine learning.

Visual Insights

#

This figure compares the performance of three different graph clustering algorithms (Bayesian MCMC, Leiden, and Spectral Clustering) on four different real-world datasets after applying three different graph sparsification techniques: metric backbone, threshold subgraph, and spectral sparsifier. The results show that both the metric backbone and the spectral sparsifier preserve the community structure well across all datasets and algorithms. In contrast, the threshold subgraph often performs poorly due to the creation of many disconnected components.

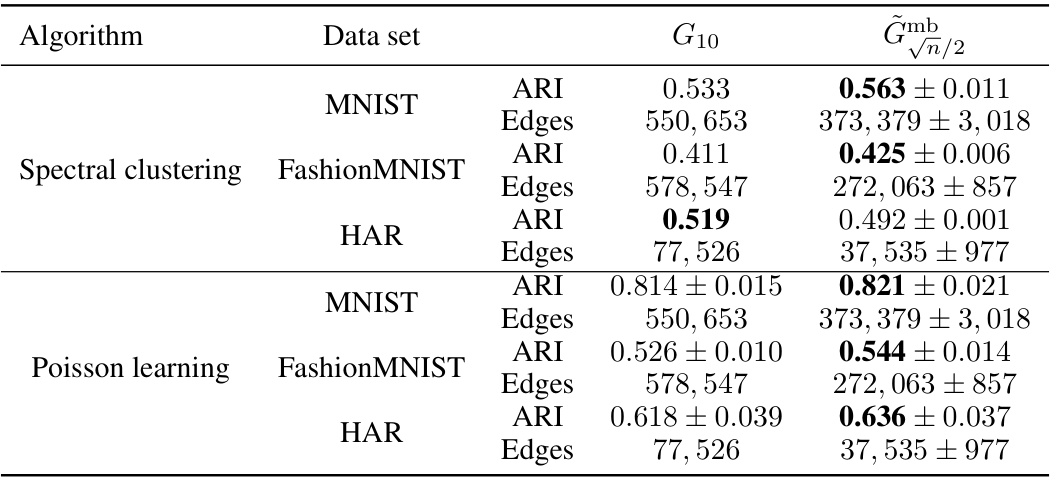
This table compares the performance of spectral clustering and Poisson learning algorithms on three datasets (MNIST, FashionMNIST, and HAR) using two different graph structures: the standard 10-nearest neighbor graph (G10) and an approximation of the metric backbone of the √n/2-nearest neighbor graph (Gmb√n/2). The metric backbone is approximated by only using 2logn shortest-path trees. The table shows the Adjusted Rand Index (ARI) and the number of edges for each algorithm and graph type. Higher ARI values indicate better community structure preservation.

In-depth insights

#

Metric Backbone Robustness

#

The concept of “Metric Backbone Robustness” in the context of network analysis focuses on how well the structural properties of a network, specifically its community structure, are preserved when the network is simplified to its metric backbone. The robustness of the metric backbone highlights the redundancy inherent in many real-world networks. The paper investigates the theoretical properties of a weighted stochastic block model and demonstrates that the metric backbone maintains community structure effectively even after a significant reduction in edges. The analysis indicates that the backbone-based approach is quite resilient to edge removal, and thus serves as a powerful tool for network sparsification. This robustness is especially significant considering the efficiency gains from sparsification; it allows for preservation of crucial information while dramatically reducing computational and storage costs. Empirical findings in various real-world datasets further support the theoretical results, confirming the metric backbone’s ability to accurately reflect community structure even in more complex networks than simple random graphs. The consistent performance across multiple clustering algorithms underscores the generalizability and practicality of using the metric backbone in community detection tasks. In summary, the research demonstrates that the metric backbone provides a robust and efficient method for analyzing network community structure.

Sparsification Techniques

#

Sparsification techniques aim to reduce the complexity of large graphs while preserving essential structural properties. The metric backbone, presented in the paper, is a prominent example, created by retaining only edges belonging to shortest paths between all node pairs. This method is parameter-free, unlike many other techniques that require tuning, and is shown to efficiently reduce graph size. Spectral sparsification is another approach, aiming to preserve the spectral properties but relying on hyperparameters for determining which edges to keep. Thresholding represents a simpler approach, but it can lead to disconnected components, harming performance. The paper’s findings highlight the superiority of the metric backbone in preserving community structure, especially when compared to other methods. The study demonstrates the robustness of the metric backbone’s community preservation and its efficiency as a sparsification technique.

Community Detection

#

Community detection, a crucial aspect of network analysis, aims to identify groups of nodes that are densely interconnected within themselves but sparsely connected to the rest of the network. The paper delves into community detection within the context of graph sparsification, particularly focusing on the metric backbone. The metric backbone, a subgraph retaining only the edges that are part of shortest paths between all node pairs, is shown to preserve community structure remarkably well. This is counterintuitive since one might expect intra-community edges to be removed disproportionately due to redundancy. The authors rigorously explore this phenomenon using a weighted stochastic block model, proving that the ratio of inter-community edges to intra-community edges remains consistent between the original and the metric backbone graphs. This is a significant finding because it demonstrates the efficiency and robustness of using the metric backbone as a sparsification technique without sacrificing crucial topological information like community structure. Furthermore, they validate their findings through extensive experiments on various real-world datasets, confirming that spectral clustering and other algorithms yield similar accuracy on the metric backbone as on the original, denser graphs. The preservation of community structure in the sparser metric backbone opens doors for more efficient clustering algorithms and network analysis in larger graphs.

Weighted SBMs

#

Weighted stochastic block models (wSBMs) extend the standard stochastic block model by incorporating edge weights, offering a more realistic representation of many real-world networks. The weights can encode various relational strengths or distances, enriching the model’s capacity to capture nuanced network structures. Analyzing wSBMs allows for a deeper understanding of community detection in weighted graphs, going beyond binary relationships. A key challenge lies in adapting community detection algorithms designed for unweighted graphs to the weighted setting. Theoretical analysis of wSBMs often involves making assumptions about the distribution of edge weights and their relationship to the underlying community structure. These assumptions can impact the results and interpretations, highlighting the need for careful consideration of the chosen model and its limitations. Furthermore, the computational complexity of analyzing wSBMs can be significantly higher compared to unweighted SBMs, particularly for large networks, demanding efficient algorithmic approaches.

q-NN Graph Analysis

#

In the realm of graph construction from data points, the q-NN (q-nearest neighbors) approach is frequently used to create proximity graphs. However, the choice of the hyperparameter q significantly impacts the graph’s structure and subsequent analyses, particularly clustering performance. A thoughtful analysis of q-NN graphs must consider the resulting edge set’s characteristics, which are affected by q. A larger q might introduce noisy edges, harming clustering accuracy. Sparsification techniques, such as creating a metric backbone, can mitigate these issues. A metric backbone, by retaining only shortest-path edges, can improve robustness to the choice of q and generate sparser, more efficient graphs for clustering algorithms. A theoretical analysis of the metric backbone in the context of stochastic block models, alongside empirical testing on diverse real-world datasets, can provide valuable insights into its performance and potential as a preprocessing step for more accurate and efficient graph clustering.

More visual insights

#

More on figures

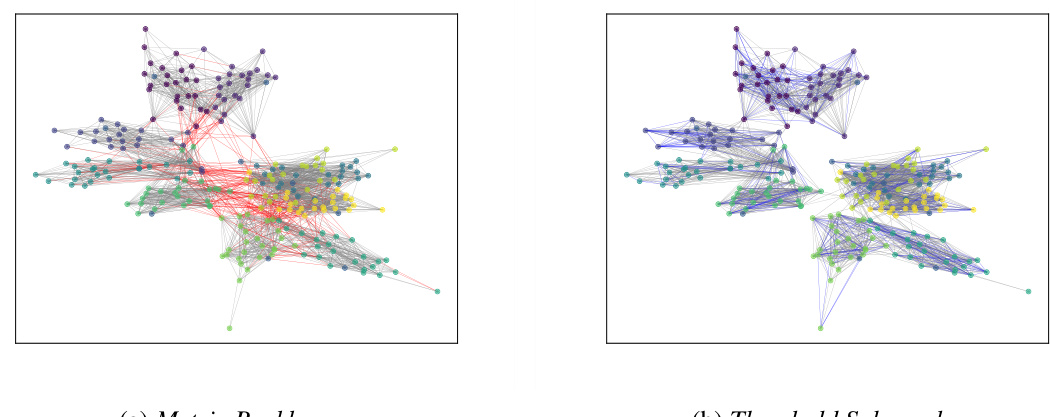
This figure shows a comparison of the Primary school dataset’s metric backbone and its thresholded subgraph. The layout is consistent across both subgraphs to facilitate comparison. Vertices are colored according to their true community assignment. Red edges represent those present in the metric backbone but absent in the thresholded subgraph, which emphasizes the importance of inter-community connections preserved by the metric backbone. Blue edges, conversely, illustrate intra-community edges retained by thresholding but removed by the metric backbone process, underscoring the reduction of intra-community edges by the backbone.

The figure shows the performance of three different clustering algorithms (Bayesian MCMC, Leiden, and Spectral Clustering) on various datasets after applying three different sparsification techniques: metric backbone, threshold subgraph, and spectral sparsifier. The results are presented in terms of Adjusted Rand Index (ARI), a measure of the similarity between two data clusterings. The figure demonstrates that the metric backbone and spectral sparsifier preserve community structure well, while thresholding leads to poor performance due to graph fragmentation.

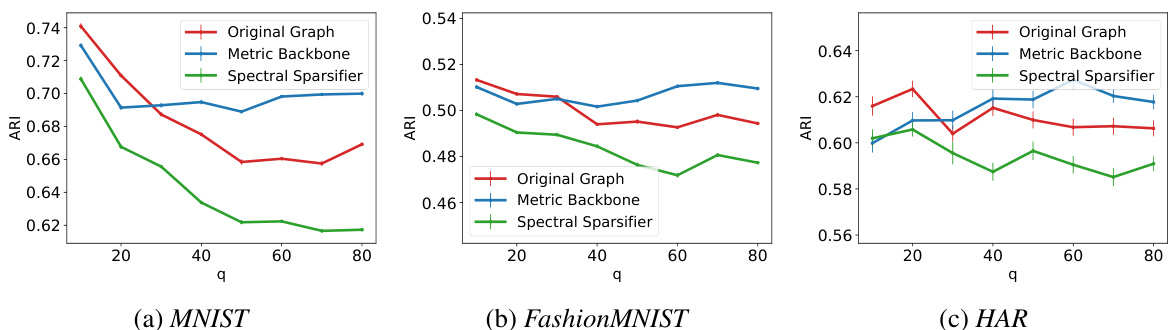
The figure displays the performance of three different graph clustering algorithms (Bayesian MCMC, Leiden, and Spectral Clustering) across three different real-world datasets (High School, Primary School, and DBLP) when applied to four different versions of the graphs: (1) the original graph, (2) the metric backbone, (3) the threshold subgraph, and (4) the spectral sparsifier. The results show that both the metric backbone and the spectral sparsifier preserve the community structure effectively, while the threshold subgraph performs poorly due to the creation of disconnected components.

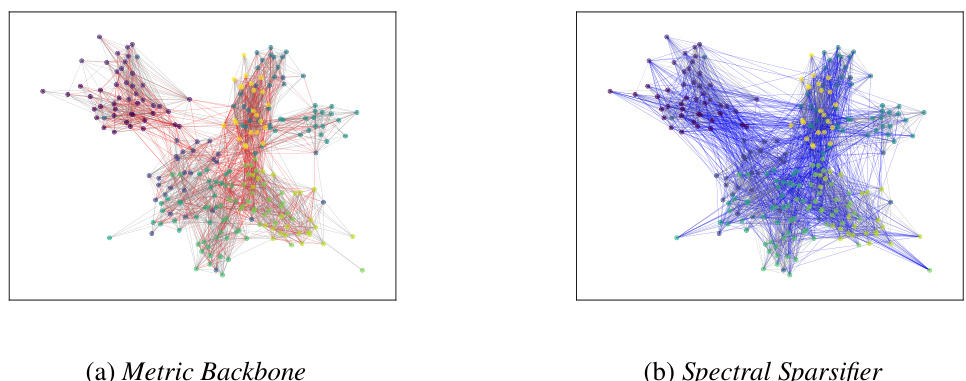
This figure compares the metric backbone and the spectral sparsification of the Primary school data set. The layout is the same for both subfigures, making comparison easy. Vertex colors indicate the true community assignments. Red edges exist in the metric backbone but not the spectral sparsifier; blue edges are in the spectral sparsifier but not the metric backbone. The figure illustrates that while both methods effectively maintain the community structure, they achieve this by preserving different sets of edges.

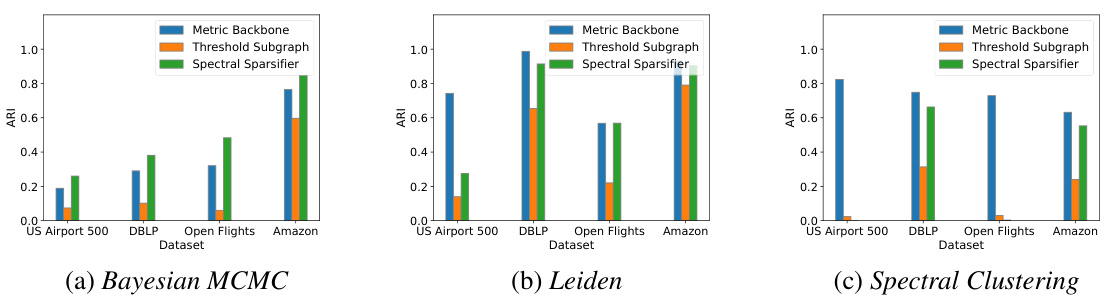
The figure shows the performance of three different graph clustering algorithms (Bayesian MCMC, Leiden, and Spectral Clustering) on various datasets after applying three different graph sparsification techniques: metric backbone, threshold subgraph, and spectral sparsifier. The results demonstrate that the metric backbone and spectral sparsification methods effectively preserve the community structure, outperforming the threshold subgraph approach, which often creates many small disconnected components.

This figure shows the number of edges in the original q-nearest neighbor graphs and their corresponding metric backbones for three datasets: MNIST, FashionMNIST, and HAR. The x-axis represents the value of q (number of nearest neighbors), and the y-axis shows the number of edges. The plots demonstrate that the metric backbone consistently contains significantly fewer edges than the original graph across all values of q and datasets. The number of edges in the original graph increases almost linearly with q. In contrast, the number of edges in the metric backbone grows much more slowly.

This figure compares the performance of three different graph clustering algorithms (Bayesian MCMC, Leiden, and Spectral Clustering) on four different real-world datasets (High School, Primary School, DBLP, and Amazon). Each algorithm was run on the original graph and three sparsified versions of the graph: the metric backbone, a threshold subgraph, and a spectrally sparsed graph. The results show that the metric backbone and the spectrally sparsed graph generally preserve the community structure as well as, or better than, the original graph, while the threshold subgraph often performs worse, likely due to creating many disconnected components.

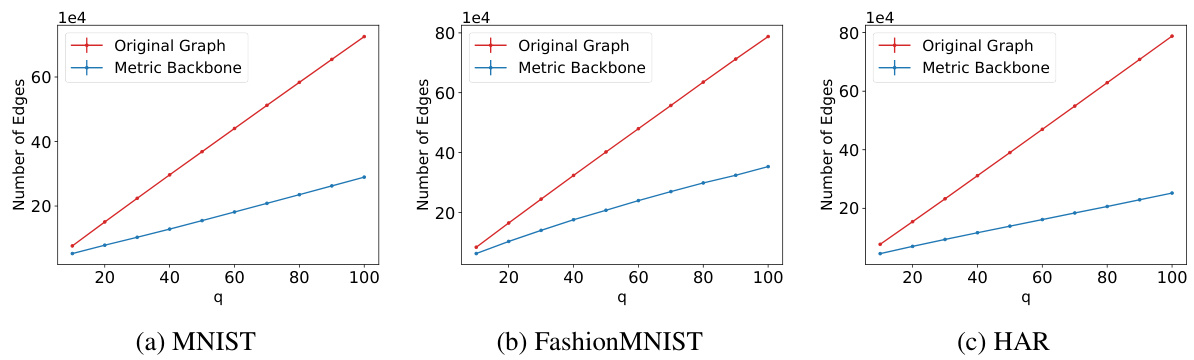
This figure shows the number of edges in the original q-nearest neighbor graph and its metric backbone for different values of q on three datasets: MNIST, FashionMNIST, and HAR. It illustrates how the metric backbone significantly reduces the number of edges compared to the original graph while preserving the community structure.

More on tables

This table presents the characteristics of four real-world networks used in the paper’s experiments. For each network, the number of nodes (n), the number of edges (|E|), the number of communities (k), and the average degree (d) are provided. The source of each dataset is also specified, noting whether the datasets are weighted (High school, Primary school) or unweighted (DBLP, Amazon).

This table shows the ratio of edges retained in the metric backbone compared to the original number of edges for four real-world datasets: High School, Primary School, DBLP, and Amazon. The metric backbone is a sparsified version of the graph containing only edges that belong to at least one shortest path between any pair of nodes. The table demonstrates that the metric backbone significantly reduces the number of edges while maintaining relevant network properties such as community structure.

Full paper

#