↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world optimization problems involve complex, poorly understood objective functions (black-box optimization). Existing methods often rely on gradient information or exact function values, which may not be available or computationally expensive. This paper tackles this challenge by focusing on optimization problems where only the order of function values can be compared (order oracle), a more realistic assumption for many applications. The limited information provided by the order oracle makes it harder to develop efficient algorithms.
The researchers introduce new algorithms that utilize only the order of objective function values to solve the optimization problems. They present both non-accelerated and accelerated algorithms for deterministic settings, demonstrating their efficiency in convex and non-convex scenarios. Importantly, they provide the first accelerated algorithm that only needs access to the order of function values. Additionally, they extend their approach to stochastic settings (noisy comparisons), providing an algorithm that converges asymptotically. These contributions significantly advance the field of black-box optimization by offering efficient and practical methods that work even with limited information.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in black-box optimization as it introduces novel, efficient algorithms using only comparison of objective function values, thus extending optimization capabilities to scenarios with limited information. It also paves the way for accelerated gradient-free methods, pushing the boundaries of optimization techniques. Its impact is significant for various applications with opaque objective functions, such as machine learning, reinforcement learning, and control systems.
Visual Insights#

The image shows Valio’s chocolate, an example used in the paper to illustrate the concept of Order Oracle. Valio, a company that uses AI in dessert creation, is referenced. The authors suggest that AI could determine optimal ingredient concentrations for customized chocolate. The Order Oracle concept is compared to determining preference order for different chocolate variations, where bounded noise is introduced to account for subjective taste variations.

The table compares the oracle complexities of various optimization methods, including those proposed in the paper, across different problem settings (non-convex, convex, strongly convex). It shows the number of oracle calls needed to achieve a certain accuracy (ε). The methods are categorized by whether they use a coordinate descent approach and/or the Order Oracle concept. It also indicates whether each method is accelerated or not.
In-depth insights#
Order Oracle: A New Frontier#
The concept of an ‘Order Oracle: A New Frontier’ in optimization presents a fascinating shift from traditional oracles. Instead of providing precise function values or gradients, it only offers comparisons, indicating which of two points yields a lower objective function value. This seemingly limited information drastically changes the optimization landscape. The core advantage lies in its robustness and applicability to black-box scenarios where function properties are unknown or difficult to compute. This makes it incredibly valuable in complex real-world optimization problems. The challenges are significant, demanding the development of entirely new algorithmic strategies that cleverly leverage the comparative information to guide the search towards the optimum. This necessitates innovative techniques, perhaps integrating binary search strategies or other comparison-based methods, to efficiently explore the solution space. Research in this area would focus on theoretical guarantees of convergence rates, particularly under noise and uncertainty in the comparison results. This would likely involve probabilistic analysis and might reveal surprising efficiency under specific conditions. Finally, practical implications would span various fields, from machine learning model selection to robotics and beyond, wherever traditional optimization techniques falter due to the lack of accessible gradient information.
Accelerated Order Methods#
Accelerated Order Methods represent a significant advancement in optimization algorithms. By leveraging only the relative order of objective function values (an “Order Oracle”) rather than precise function values or gradients, these methods sidestep the limitations of traditional gradient-based approaches. The key innovation lies in integrating the Order Oracle into existing optimization frameworks, specifically coordinate descent methods. This approach cleverly uses linear search, guided by the Order Oracle, to adaptively determine both the optimal step size and the most beneficial coordinate to update. The resulting algorithms demonstrate state-of-the-art convergence rates in various convexity settings, even achieving acceleration in strongly convex scenarios. A notable contribution is the development of the first accelerated algorithm using the Order Oracle, highlighting the potential of this novel approach to outperform conventional methods in situations where gradient information is unavailable or computationally expensive. Further research is needed to explore the broader implications and explore the limits of accelerated Order Methods, especially considering noisy oracles and high-dimensional problems.
Stochastic Order Analysis#
A section on “Stochastic Order Analysis” in a research paper would likely delve into the probabilistic properties of order relationships between random variables. This could involve exploring various stochastic orders (e.g., first-order stochastic dominance, likelihood ratio order) to compare the distributions of random variables. The analysis might focus on deriving properties or inequalities related to these stochastic orders, perhaps under specific assumptions on the distributions involved. Applications could range from analyzing queuing systems and reliability models to financial risk management and decision making under uncertainty. The results could be theoretical, establishing new relationships between stochastic orders, or applied, demonstrating the usefulness of such orders in specific contexts. A key aspect might involve the development of statistical tests for comparing the stochastic order of two samples of data. This could include establishing the power and efficiency of the proposed tests. The presence of noise or uncertainty in the observed data would be a critical consideration, leading to robust statistical methods. The overall goal would be to provide a more nuanced understanding of the order structure in stochastic systems.
Limitations and Future Work#
A research paper’s ‘Limitations and Future Work’ section is crucial for assessing its impact and guiding future research. Limitations might include the scope of the study (e.g., specific datasets, algorithms, or problem settings), assumptions made (e.g., data distribution, noise levels), and the methodology’s limitations (e.g., computational complexity, convergence guarantees). Addressing these limitations is vital; for instance, testing the robustness of algorithms under more realistic conditions, investigating the influence of model parameters, or proposing alternative methods to overcome inherent challenges are important aspects. Future work could focus on extending the methodology to broader application areas, developing more efficient or scalable algorithms, or tackling more complex problems. The discussion should also mention the generalizability of findings to different domains, the potential for improvements in theoretical analysis, and the exploration of new techniques to enhance the results obtained. A strong ‘Limitations and Future Work’ section enhances the credibility and value of a research paper by acknowledging its boundaries and pointing towards promising avenues for future research.
Numerical Experiments#
The Numerical Experiments section is crucial for validating the theoretical claims of the paper. It should demonstrate the effectiveness of the proposed algorithms by comparing their performance against state-of-the-art methods on representative problem instances. A rigorous experimental setup is vital, including a clear description of the benchmark problems, evaluation metrics, and the parameter settings used. The results should be presented in a clear and concise manner, ideally with visualizations like graphs to facilitate understanding. Statistical significance testing should be employed to ensure that observed differences are not due to random chance. Furthermore, the discussion of results should go beyond simply reporting the numbers; it needs to connect the experimental findings back to the theoretical analysis, highlighting any agreement or discrepancies. Finally, attention should be paid to the computational cost of the proposed algorithms, comparing their runtime against existing methods and exploring any scalability issues. A thorough analysis in this section builds trust in the validity and practical relevance of the research.
More visual insights#
More on figures

This figure compares the convergence performance of the proposed OrderRCD and OrderACDM algorithms against existing state-of-the-art non-accelerated first-order algorithms such as RCD (random coordinate descent) and GD (gradient descent). The results show that OrderRCD, despite its limitations in using only an order oracle, performs surprisingly well, even exceeding the performance of RCD. Importantly, OrderACDM demonstrates the benefit of acceleration, converging significantly faster than the other non-accelerated methods. This visualization confirms the theoretical findings presented in the paper, highlighting the effectiveness of the proposed approach and the existence of acceleration with order oracles.
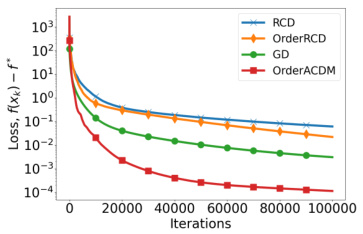
This figure compares the performance of four different optimization algorithms: random coordinate descent (RCD), random coordinate descent with order oracle (OrderRCD), gradient descent (GD), and accelerated coordinate descent with order oracle (OrderACDM). The y-axis represents the loss function value (f(x) - f*), and the x-axis represents the number of iterations. The graph shows that OrderACDM converges the fastest, demonstrating acceleration. OrderRCD performs comparably to RCD, showcasing that the Order Oracle approach maintains competitive convergence rates compared to standard first-order methods.

The image shows a prototype of a smart coffee machine. The machine is designed to make personalized coffee drinks by automatically adjusting ingredient ratios based on user preferences. This aligns with the paper’s Order Oracle concept, which relies on comparing the preferences of different coffee recipes without knowing the exact values of their objective function.

This figure shows a 3D model of a smart coffee machine designed to create customized coffee drinks. The design incorporates various mechanisms to precisely control the proportions of different ingredients, such as coffee beans (Robusta and Arabica), milk, cream, sugar, and other flavorings. The aim is to provide the optimal level of bitterness, strength, milkiness, and sweetness based on individual preferences.
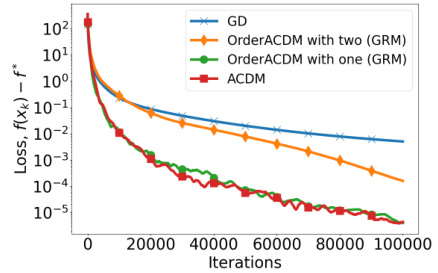
The figure compares the convergence performance of OrderRCD (random coordinate descent with order oracle) and OrderACDM (accelerated coordinate descent method with order oracle) against standard gradient descent (GD) and RCD (random coordinate descent) methods. It showcases that OrderRCD outperforms RCD, and importantly, that OrderACDM (with a single golden ratio method call) demonstrates acceleration over its non-accelerated counterparts, achieving faster convergence rates.
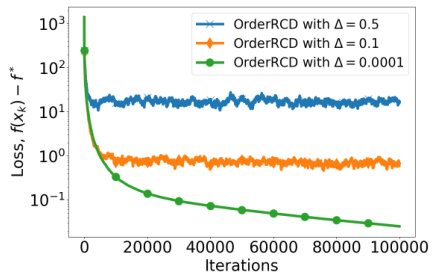
The figure shows how adversarial noise affects the convergence of the OrderRCD algorithm. Three lines represent OrderRCD performance with different maximum noise levels (Δ = 0.5, 0.1, 0.0001). The plot demonstrates that higher noise levels lead to slower convergence and a higher final loss (the difference between the algorithm’s final objective function value and the optimal value). The algorithm still converges, but the accuracy is impacted by noise.
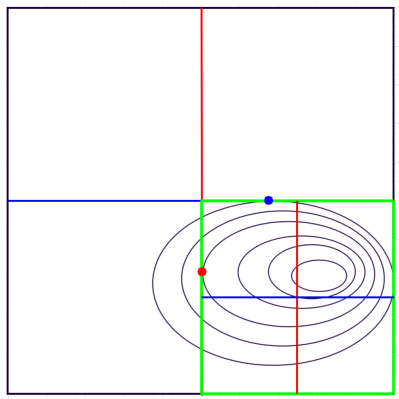
This figure illustrates the ‘Private Communication’ approach described in Appendix G. It shows how a low-dimensional optimization problem is solved iteratively using the Order Oracle. The algorithm starts with a square containing the minimum of a convex Lipschitz function. Lines are drawn to divide the space and the one-dimensional optimization problem is solved along these lines, reducing the search space. The algorithm repeats this process, halving the search area until the minimum is found within a desired accuracy.
Full paper#



















