Deep Homomorphism Networks

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with graph neural networks (GNNs) because it introduces a novel GNN layer, the graph homomorphism layer, which significantly improves GNNs’ ability to detect subgraph patterns. It also provides a useful theoretical framework for analyzing the expressive power of GNNs, which is highly relevant to ongoing efforts to enhance their capabilities. The proposed model is computationally efficient, making it practical for real-world applications involving large graphs. Furthermore, it provides a new direction for the design of GNNs.

Visual Insights

#

The figure illustrates a Deep Homomorphism Network (DHN) architecture with two layers. The first layer uses 3-cycles (C3) as patterns to detect local subgraph structures, and the second layer uses 2-cycles (C2). The combination of these layers enables the detection of more complex patterns (like the ‘spoon’ pattern shown) not explicitly specified in the pattern set. The shaded areas represent the ‘receptive field’ of each layer, showing how the pattern detection works cumulatively.

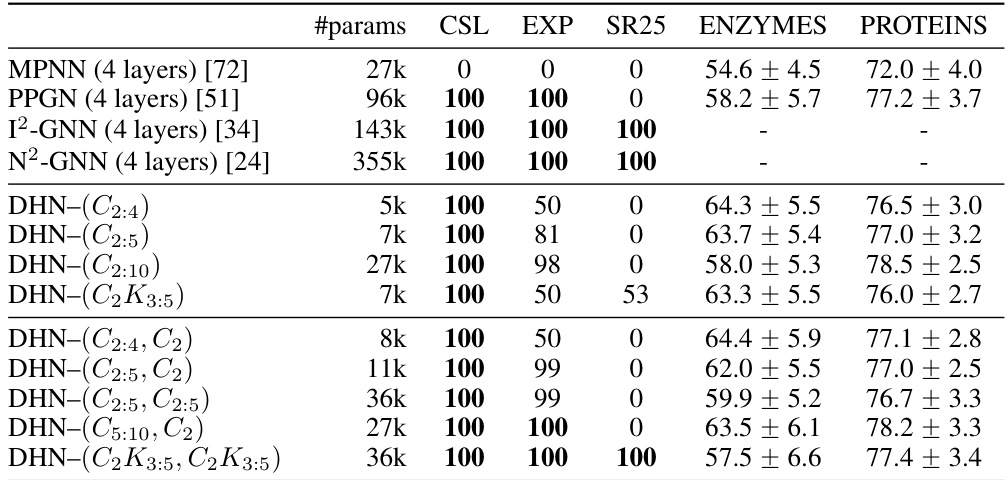
This table presents the classification accuracy results of different Graph Neural Network (GNN) models on several benchmark datasets. The datasets include both synthetic datasets designed to test the expressive power of GNNs (CSL, EXP, SR25) and real-world datasets for protein function prediction (ENZYMES, PROTEINS). The table shows the number of parameters for each model and their respective accuracy (Acc.%) on each dataset. The results highlight the performance of the proposed Deep Homomorphism Network (DHN) model in comparison to existing GNNs.

In-depth insights

#

DHN Architecture

#

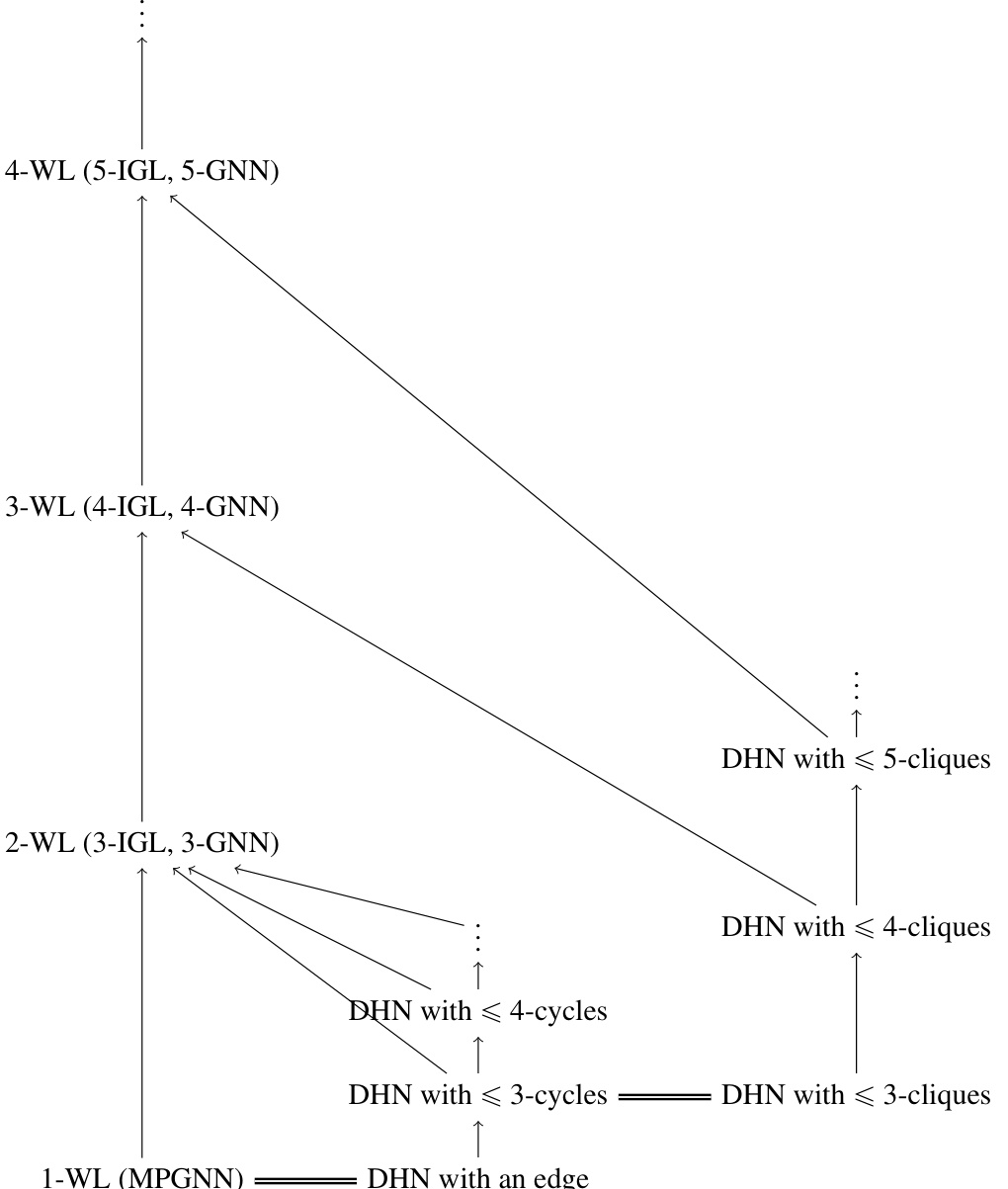
The Deep Homomorphism Network (DHN) architecture is built upon the concept of stacking graph homomorphism layers. Each layer efficiently enumerates local subgraph patterns matching a predefined set, applying non-linear transformations to node features and aggregating them based on pattern matches. This modular design allows for flexible control over the network’s expressive power by carefully selecting the subgraph patterns used in each layer. The stacking of these layers creates a deep architecture that can detect complex patterns not expressible by shallow models. Crucially, the DHN’s computational efficiency is directly tied to the time complexity of finding graph homomorphisms, making it a practical and lightweight approach, especially for large real-world graphs. By leveraging domain knowledge to select meaningful patterns, the DHN architecture effectively tackles difficult graph-based problems often intractable for standard methods. This combination of expressive power, efficiency, and domain adaptability makes the DHN architecture a compelling and innovative contribution to the field of graph neural networks.

Expressive Power

#

The research paper delves into the expressive power of Graph Neural Networks (GNNs), specifically focusing on their ability to detect subgraph patterns. A key limitation of many GNNs is their inability to effectively capture complex, non-tree-like patterns. The authors introduce a novel GNN layer, the graph homomorphism layer, designed to systematically enumerate and process local subgraph patterns. This approach allows for the theoretical characterization of the GNN’s expressive power, directly linked to the set of patterns used, and facilitates the creation of a deep GNN model (DHN) that stacks these layers. The DHN offers a flexible framework for analyzing expressive power by exploring the trade-off between the expressiveness of a model and the computational cost of evaluating that expressiveness. Furthermore, the paper establishes a connection between the DHN’s expressive power and graph homomorphism indistinguishability, providing a valuable tool for comparing the capabilities of various GNN architectures. The experimental results demonstrate that the DHN, while not always outperforming state-of-the-art models, demonstrates promising performance in specific problem domains and requires fewer parameters. The theoretical framework of homomorphism distinguishability offers a strong foundation for analyzing and improving GNN expressive power.

Computational Cost

#

The computational cost of graph neural networks (GNNs) is a critical factor, especially when dealing with large graphs. Many existing GNNs, particularly those that explicitly aim for high expressive power, have a computational complexity that scales poorly with graph size, making them unsuitable for real-world applications involving massive datasets. The paper’s proposed Deep Homomorphism Network (DHN) addresses this by directly incorporating domain knowledge into the model architecture. This approach, which leverages graph homomorphisms to enumerate local subgraph patterns, provides a trade-off between expressive power and computational efficiency. While computing graph homomorphisms can be computationally expensive in general, the DHN model showcases how this task can be optimized under certain assumptions, like those of bounded degree, bounded treewidth, or bounded degeneracy in graphs. These scenarios significantly reduce the computational burden, making the approach viable for practical use. The paper emphasizes the importance of this trade-off, showing that while the DHN may not match the expressive power of some more complex GNNs in all cases, it offers a substantial performance advantage in many real-world scenarios by reducing the computational cost considerably.

Empirical Results

#

An Empirical Results section in a research paper would ideally present a detailed analysis of experimental findings, comparing the proposed method’s performance against baselines across multiple metrics. Key aspects to cover would include the datasets used, providing sufficient details for reproducibility, and clearly stating evaluation metrics. The results should be presented concisely yet comprehensively, with tables and figures that are easy to interpret. A discussion of statistical significance is crucial, including error bars or other measures of variability to demonstrate the reliability of results. The analysis should move beyond simple comparisons to explore trends and relationships, potentially visualizing performance across different parameter settings or dataset characteristics. Any unexpected or surprising findings should be highlighted and discussed. Finally, a thoughtful explanation of the results, relating them back to the paper’s central claims and hypotheses, is essential for a strong and persuasive Empirical Results section.

Future Directions

#

The paper’s ‘Future Directions’ section could explore several promising avenues. Extending the DHN model to handle more complex graph structures beyond those with bounded treewidth or degeneracy is crucial for broader applicability. This might involve incorporating techniques from higher-order GNNs or developing novel aggregation schemes that are both expressive and computationally efficient. Investigating the theoretical limits of DHN’s expressive power is another key area. Further analysis of its relationship to existing GNN models using more sophisticated tools from graph theory could provide a deeper understanding of its strengths and weaknesses. Developing more efficient algorithms for computing generalised homomorphism numbers is also essential, particularly for extremely large graphs where current methods may be too computationally expensive. Finally, applying DHN to a wider variety of real-world problems and comparing its performance to state-of-the-art GNN models across different benchmarks would strengthen its practical value. The focus should be on applications where subgraph pattern recognition is paramount, such as in social network analysis, bioinformatics, and knowledge graphs.

More visual insights

#

More on figures

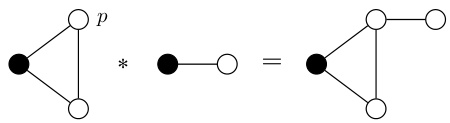
The figure illustrates a Deep Homomorphism Network (DHN) with two layers. Each layer uses a different set of homomorphism patterns (C3 and C2). The input graphs are processed through these layers, and the output shows that the DHN can detect a new pattern, which is named ‘spoon’, that is not explicitly defined in the model. The illustration demonstrates that by stacking different homomorphism patterns, the DHN can learn to detect complex patterns.

This figure illustrates the architecture of a Deep Homomorphism Network (DHN) built using two homomorphism layers (C3 and C2). It demonstrates how stacking different homomorphism layers enables the detection of complex patterns, such as the ‘spoon’ pattern, which are not explicitly specified in the model. This highlights the ability of DHNs to learn complex graph structures by combining simpler patterns.

More on tables

This table presents the classification accuracy (in percentage) achieved by various Graph Neural Network (GNN) models on synthetic and real-world datasets. The synthetic datasets (CSL, EXP, SR25) are designed to evaluate the expressive power of GNNs, while the real-world datasets (ENZYMES, PROTEINS) represent real-world problems in bioinformatics. The table shows the performance of several GNN models, including different variants of the proposed Deep Homomorphism Network (DHN), in terms of accuracy and the number of parameters used.

This table presents the classification accuracy results of various Graph Neural Network (GNN) models on three synthetic benchmark datasets (CSL, EXP, SR25) and two real-world datasets (ENZYMES, PROTEINS). The synthetic datasets are designed to evaluate the expressive power of GNNs, while the real-world datasets assess the performance on practical graph classification tasks. The table shows the accuracy (in percentage) achieved by each model, along with the number of parameters used in each model. This allows for comparison of model performance in terms of both accuracy and model complexity.

This table presents the classification accuracy results of various GNN models on synthetic and real-world datasets. The synthetic datasets (CSL, EXP, SR25) are designed to evaluate the expressive power of GNNs, while the real-world datasets (ENZYMES, PROTEINS) represent protein function prediction tasks. The table shows the performance of different models, including MPNN, PPGN, I2-GNN, N2-GNN, and various configurations of the proposed DHN model. The results are reported in terms of accuracy (%), along with the number of parameters used by each model.

Full paper

#