↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Offline reinforcement learning struggles with limited and suboptimal data, hindering accurate policy learning. Existing data augmentation methods often fail to directly improve data quality. This paper tackles these issues head-on.
The paper introduces Generative Trajectory Augmentation (GTA), a novel approach using conditional diffusion models to generate high-reward and dynamically plausible trajectories. GTA partially adds noise to existing trajectories and then denoises them using classifier-free guidance, conditioned by the amplified return value. This process effectively guides trajectories towards high-reward regions.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel data augmentation method for offline reinforcement learning, addressing a critical challenge in the field. By improving data quality, the method enhances the performance of various offline RL algorithms, potentially accelerating the development of more effective and robust AI agents. This has relevance for various domains involving limited or costly online interaction. It also opens new avenues for research on generative models and offline RL.
Visual Insights#
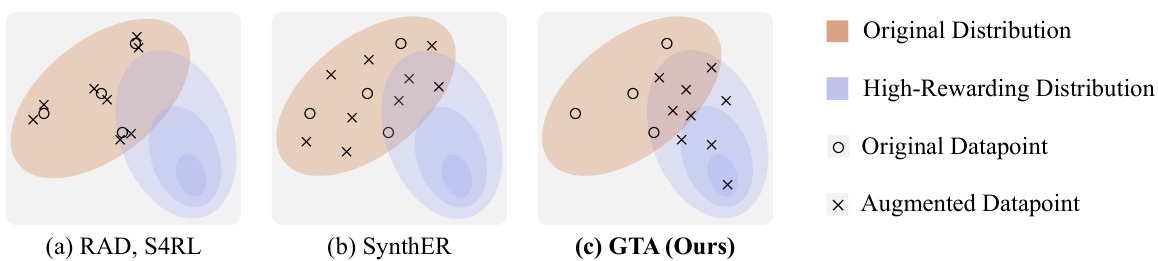
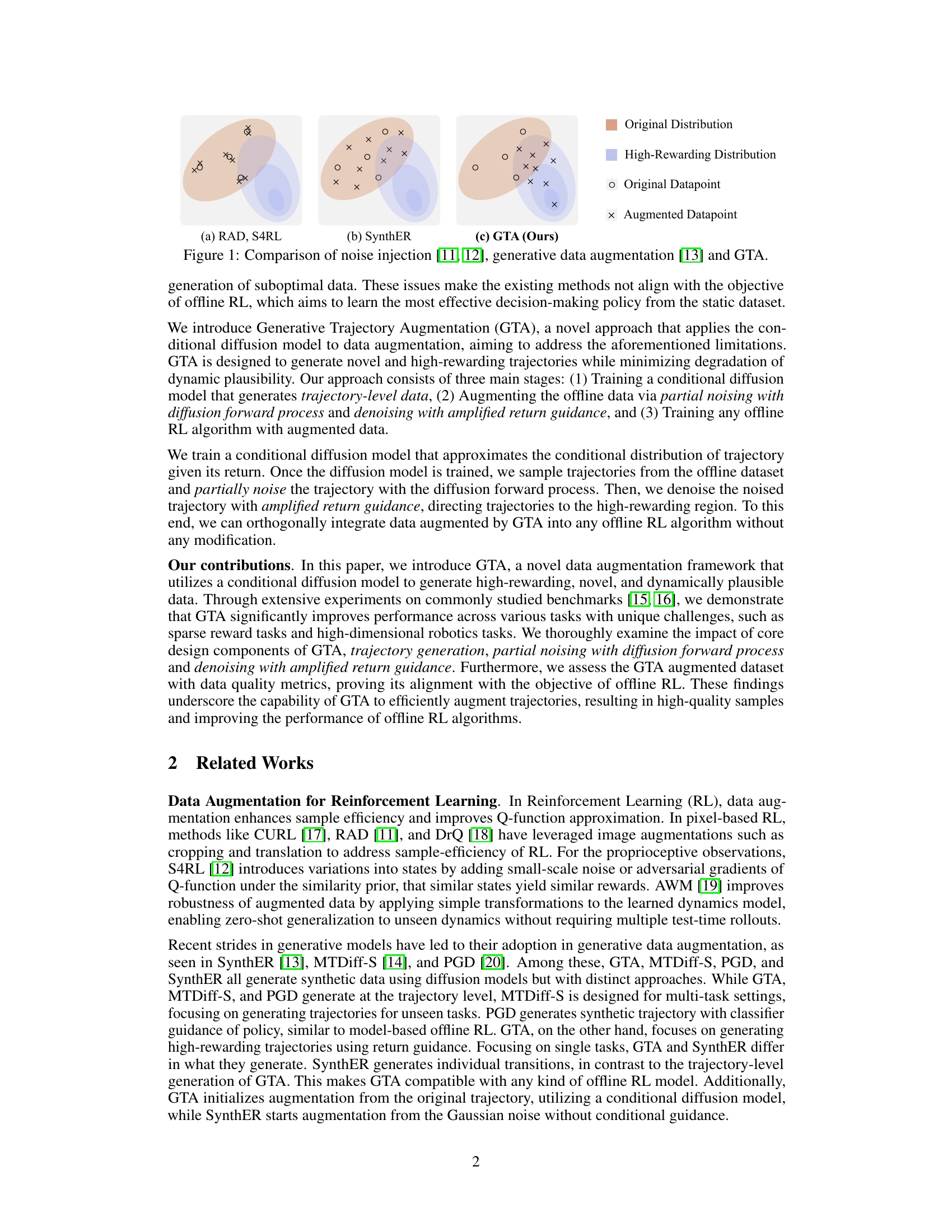
This figure compares three different data augmentation methods for offline reinforcement learning: noise injection (e.g., RAD, S4RL), generative data augmentation (e.g., SynthER), and the proposed Generative Trajectory Augmentation (GTA). It visually represents how each method augments the original data distribution (represented by beige ellipses) to include high-rewarding datapoints (represented by blue ellipses). Noise injection methods add minimal noise to existing data points, while generative methods synthesize new data points, often with limited success in exploring high-reward areas. GTA is shown to generate new high-rewarding datapoints that are plausibly connected to the original data, better aligning with the aims of offline RL.

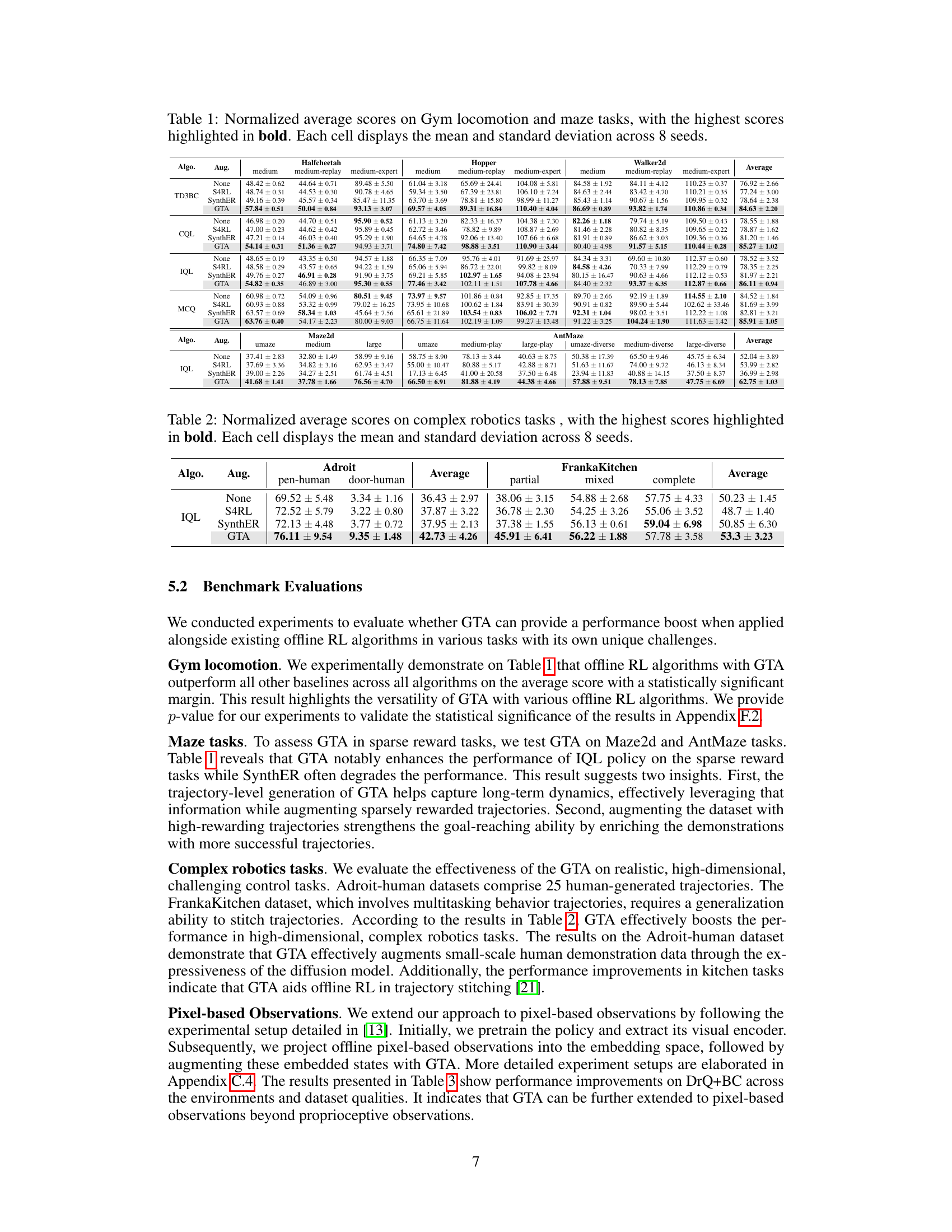
This table presents the average normalized scores achieved by different offline reinforcement learning algorithms on various Gym locomotion and maze tasks. The algorithms are tested with and without data augmentation techniques (None, S4RL, SynthER, and GTA). The scores represent the mean and standard deviation across eight independent random seeds, highlighting the effectiveness of different methods. The highest score for each task and algorithm is shown in bold.
In-depth insights#
Offline RL Challenges#
Offline reinforcement learning (RL) presents unique challenges stemming from the reliance on fixed datasets, eliminating the possibility of online interactions and feedback. This limitation directly impacts the ability of algorithms to explore the state-action space fully, leading to potential issues like overestimation of Q-values in unseen regions (extrapolation error). The quality and representativeness of the offline data are critical; insufficient or biased data may prevent the learner from finding optimal policies. Data augmentation techniques are crucial for improving offline RL performance, but existing methods often fall short of directly addressing the fundamental data limitations. Furthermore, the reward function’s quality and sparsity are major issues. Sparse rewards can make learning significantly harder because it is difficult for the agent to learn to find rewarding actions without frequent interaction with the environment. The high dimensionality of the state and action spaces in many real-world RL problems further compounds the challenges. Novel methods for data augmentation that guarantee better state coverage and reward characteristics are essential to overcome these difficulties.
Generative Augmentation#
Generative augmentation, in the context of reinforcement learning, presents a powerful paradigm shift from traditional data augmentation methods. Instead of simply adding noise or making minor alterations to existing data, generative methods create entirely new, synthetic data points. This offers the advantage of expanding the state-action space and potentially discovering regions under-represented in the original dataset. A well-designed generative model can learn the underlying data distribution and produce samples that resemble real data, improving the accuracy and coverage of the training dataset. However, challenges exist. Ensuring the generated data is realistic and does not introduce biases or artifacts is crucial for preventing the model from learning spurious correlations or overfitting to synthetic data. Therefore, careful consideration of the generative model’s design, training process, and evaluation metrics are vital. The success of generative augmentation significantly depends on the ability of the model to capture the intricate dynamics of the environment, leading to improved decision making and sample efficiency in reinforcement learning algorithms.
Diffusion Model Use#
The utilization of diffusion models in the research paper presents a novel approach to data augmentation for offline reinforcement learning. The core idea is to leverage the ability of diffusion models to generate realistic and high-rewarding trajectories. This is achieved by partially adding noise to original trajectories and then denoising them with guidance, pushing them towards the high-rewarding regions. The process strategically balances exploration and exploitation. By training a conditional diffusion model, the method produces trajectories that align with desired rewards, increasing the overall quality of the offline data. This approach contrasts with traditional data augmentation methods by generating novel and diverse data, not just noisy modifications of the originals. Furthermore, the methodology seamlessly integrates with existing offline reinforcement learning algorithms, making it a versatile and easily adaptable tool.
Trajectory-Level Data#
Trajectory-level data augmentation, as explored in this research, presents a significant advancement over traditional methods. Instead of treating individual data points in isolation, it leverages the inherent temporal dependencies within sequences of state-action-reward transitions. This approach is particularly beneficial for reinforcement learning tasks, where the sequential nature of interactions is crucial. By modeling entire trajectories, the method captures long-term dependencies that are often missed by simpler approaches. This holistic perspective allows for the generation of more realistic and plausible synthetic data, enriching the training dataset and improving the performance of offline reinforcement learning algorithms. The method’s strength lies in its capacity to generate high-rewarding, yet dynamically consistent, trajectories, which is critical for improving the overall quality of the data used for training and subsequently, the performance of the trained model. However, careful consideration must be given to the balance between exploration (generating novel trajectories) and exploitation (focusing on high-reward regions), since an overemphasis on one could compromise the quality of the generated data.
Future Work#
Future research directions stemming from this Generative Trajectory Augmentation (GTA) method could explore several promising avenues. Extending GTA’s applicability to more complex environments with intricate dynamics, such as those involving multi-agent interactions or continuous control problems, presents a significant challenge and opportunity. Investigating alternative guidance mechanisms beyond amplified return conditioning could further refine the quality and diversity of generated trajectories. This could involve incorporating reward shaping techniques or integrating model-based methods for more accurate prediction of future rewards. A crucial area for improvement is enhancing the sample efficiency of GTA itself. Currently, the method demands significant computational resources for training the diffusion model, and ways to reduce this computational load are urgently needed. Finally, a thorough exploration of the trade-off between exploration and exploitation when augmenting offline data using GTA is essential. This nuanced understanding could result in more effective hyperparameter tuning for diverse offline reinforcement learning tasks.
More visual insights#
More on figures
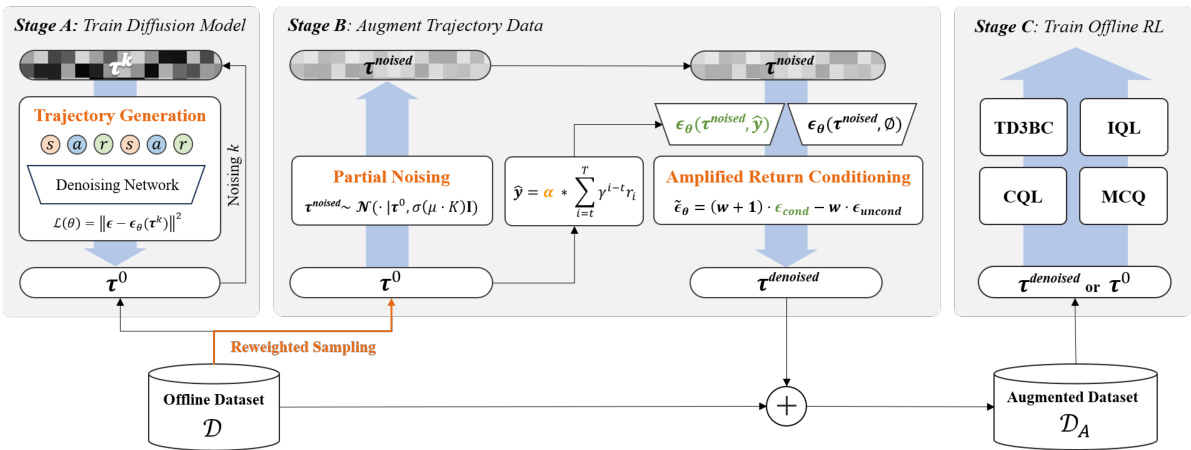
This figure illustrates the three main stages of the Generative Trajectory Augmentation (GTA) method. Stage A involves training a conditional diffusion model to generate trajectories. Stage B augments the trajectories by partially adding noise using a diffusion model’s forward process and then denoising it with amplified return guidance (pushing trajectories towards higher rewards). Stage C uses the augmented dataset to train offline reinforcement learning (RL) algorithms (TD3BC, IQL, CQL, MCQ).
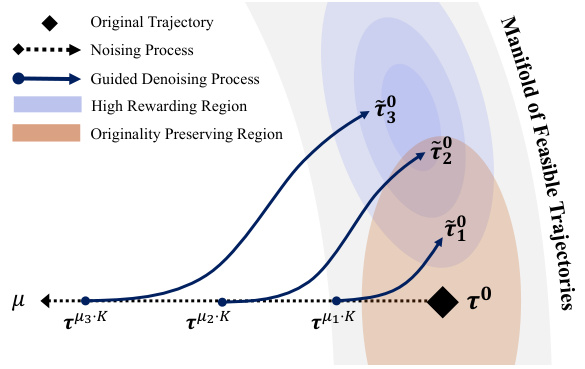
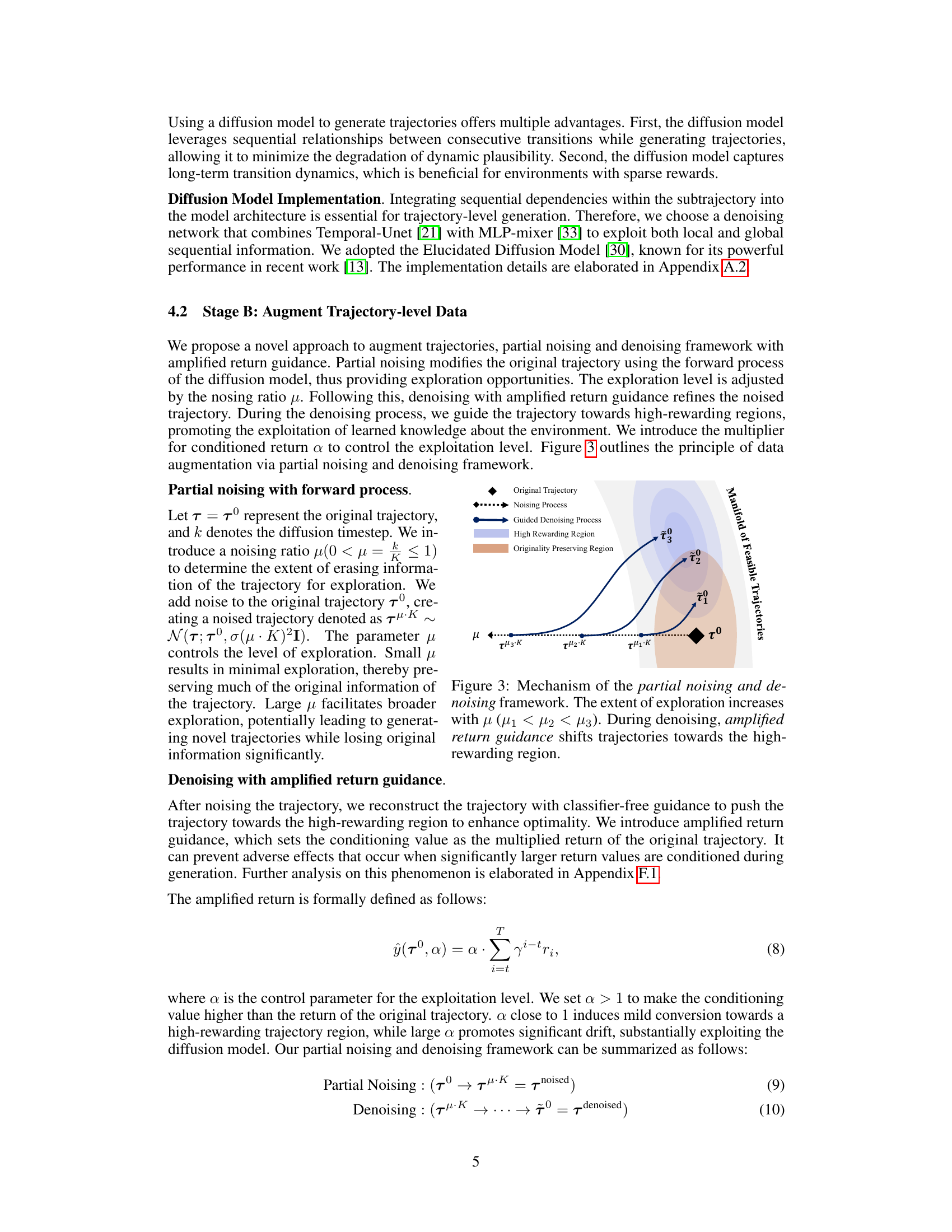
This figure illustrates the mechanism of GTA’s data augmentation process, which involves two main steps: partial noising and guided denoising. The partial noising process adds noise to the original trajectory, controlled by the parameter μ, allowing for exploration of new state-action spaces. The level of exploration increases as μ increases. The guided denoising process uses amplified return guidance to direct the trajectory towards high-rewarding areas, enhancing exploitation of already learned knowledge. The figure visually represents this process by showing how trajectories are shifted towards the high-rewarding region during denoising, while preserving plausibility by starting from a partially noised version of the original trajectory.
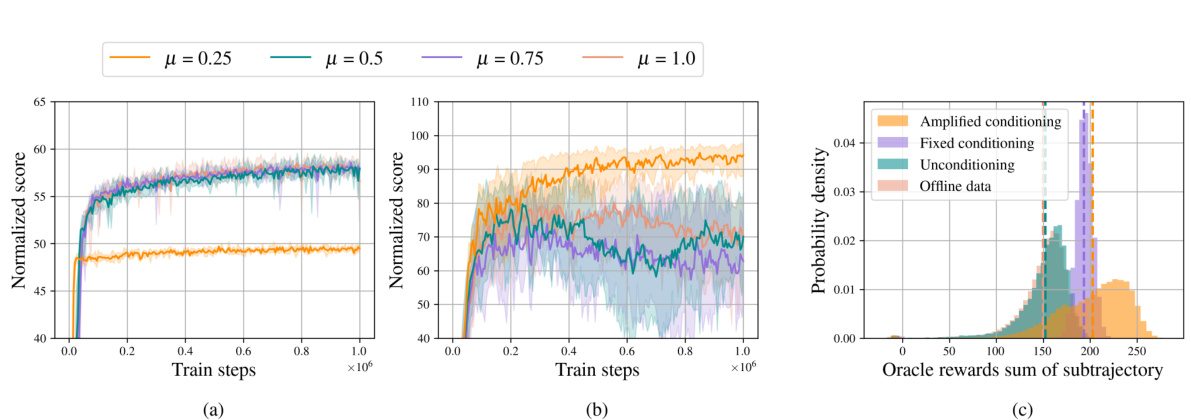
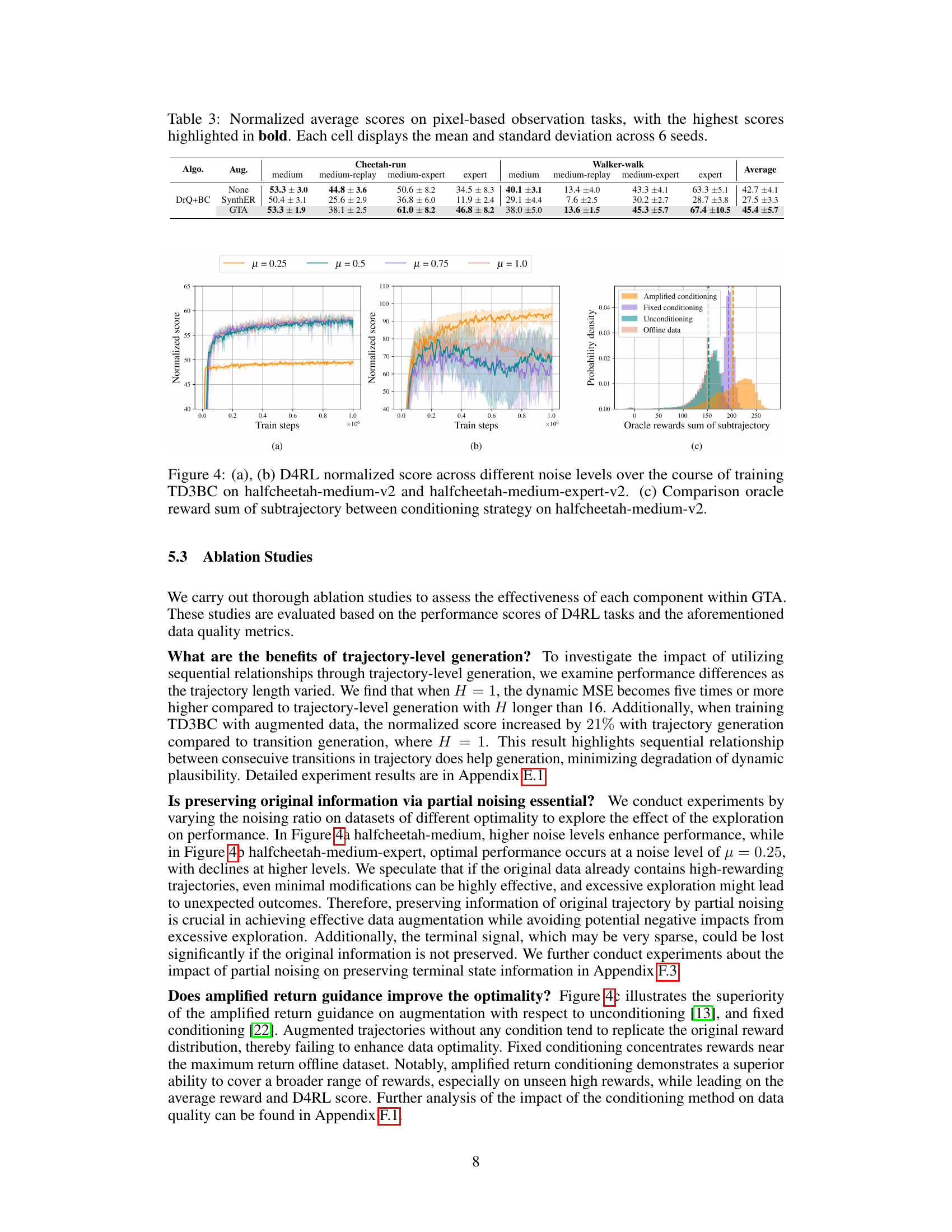
This figure demonstrates the ablation study on the impact of partial noising (different noise levels) and amplified return guidance. (a) and (b) show the training curves of TD3BC on two different D4RL datasets (halfcheetah-medium-v2 and halfcheetah-medium-expert-v2) with various noise levels. (c) shows the distribution of oracle rewards (sum of subtrajectories) for three different conditioning strategies: amplified conditioning (GTA), fixed conditioning, and unconditioning.
This figure compares three different data augmentation methods: noise injection, generative data augmentation, and the proposed Generative Trajectory Augmentation (GTA). Noise injection adds small noise to existing data, leading to only minimal improvement. Generative data augmentation generates new data points, but it is limited by the original data distribution. GTA leverages a diffusion model to create trajectories that are both high-rewarding and dynamically plausible, outperforming the other methods.

This figure illustrates the mechanism of GTA’s partial noising and denoising framework. The left part shows how partial noising with different noise levels (μ) increases the exploration of the trajectory generation process. The right part shows how the denoising with amplified return guidance pushes the noised trajectory towards the high-rewarding region. The manifold of feasible trajectories is shown to indicate the relationship between the original trajectory and the generated trajectory.
This figure compares three different data augmentation methods: noise injection, generative data augmentation, and the proposed Generative Trajectory Augmentation (GTA). Noise injection adds minimal noise to the existing data, resulting in small local changes. Generative data augmentation synthesizes new data points, but these points tend to cluster near the original data distribution. GTA generates high-rewarding trajectories that are dynamically plausible while exploring novel states or actions.
The figure illustrates the three main stages of the Generative Trajectory Augmentation (GTA) method. Stage A involves training a conditional diffusion model that can generate trajectories. Stage B uses this model to augment the offline data. It partially adds noise to the original trajectories using the diffusion forward process, then denoises them with classifier-free guidance conditioned on amplified return values, guiding the trajectories towards high-rewarding regions. Finally, Stage C trains an offline reinforcement learning algorithm using the augmented dataset.
This figure illustrates the three main stages of the Generative Trajectory Augmentation (GTA) method. Stage A involves training a conditional diffusion model to generate trajectories. Stage B augments the trajectories by partially adding noise using a diffusion process, then denoising using amplified return guidance to direct the trajectories towards higher rewards. Finally, Stage C uses the augmented dataset to train various offline reinforcement learning (RL) algorithms. The figure shows a visual representation of data flow between the stages and the processes involved.
This figure shows the ablation study of the noising ratio (μ) and amplified return guidance on the halfcheetah environment. (a) and (b) are learning curves of TD3BC trained with different levels of noising ratios on halfcheetah-medium-v2 and halfcheetah-medium-expert-v2. (c) shows the distribution of oracle rewards from the offline dataset, generated trajectories using fixed guidance, amplified return guidance and unconditioning.
This figure compares three different data augmentation methods: noise injection, generative data augmentation, and the proposed method, Generative Trajectory Augmentation (GTA). Noise injection adds minimal noise to the existing data, resulting in only minor changes and limited exploration. Generative data augmentation uses a generative model to create new data, but it is constrained by the distribution of the existing data. GTA, on the other hand, uses a diffusion model to generate new and high-rewarding trajectories that are both plausible and dynamic. The figure shows that GTA is able to generate data that is significantly different from the original data and that it is better at exploring the state-action space.
More on tables

This table presents the average performance scores of different offline reinforcement learning algorithms on complex robotics tasks. The algorithms are tested with and without data augmentation using GTA, S4RL, and SynthER. The table shows the mean and standard deviation of the scores across 8 different random seeds. The tasks included are Adroit (pen-human and door-human) and FrankaKitchen (partial, mixed, and complete). The bold values represent the best-performing methods for each task.

This table presents the results of experiments conducted on pixel-based observation tasks using different data augmentation methods and offline reinforcement learning algorithms. The table shows the average scores achieved by each method across various datasets (medium, medium-replay, medium-expert, and expert). Higher scores indicate better performance.

This table presents the results of experiments conducted on various Gym locomotion and maze tasks using different offline reinforcement learning algorithms. The algorithms were tested with and without data augmentation techniques (None, S4RL, SynthER, and GTA). The table shows the normalized average scores achieved by each algorithm on each task. The highest scores for each task are bolded. The mean and standard deviation of the scores across eight different random seeds are reported for each algorithm and augmentation method.

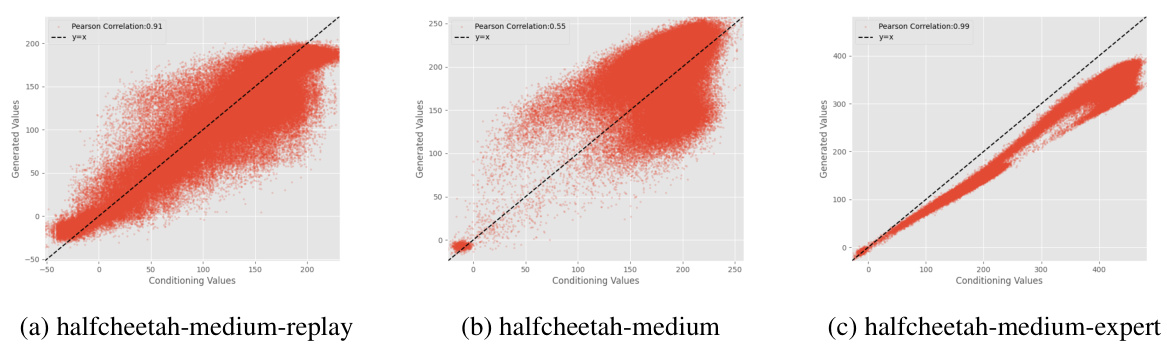
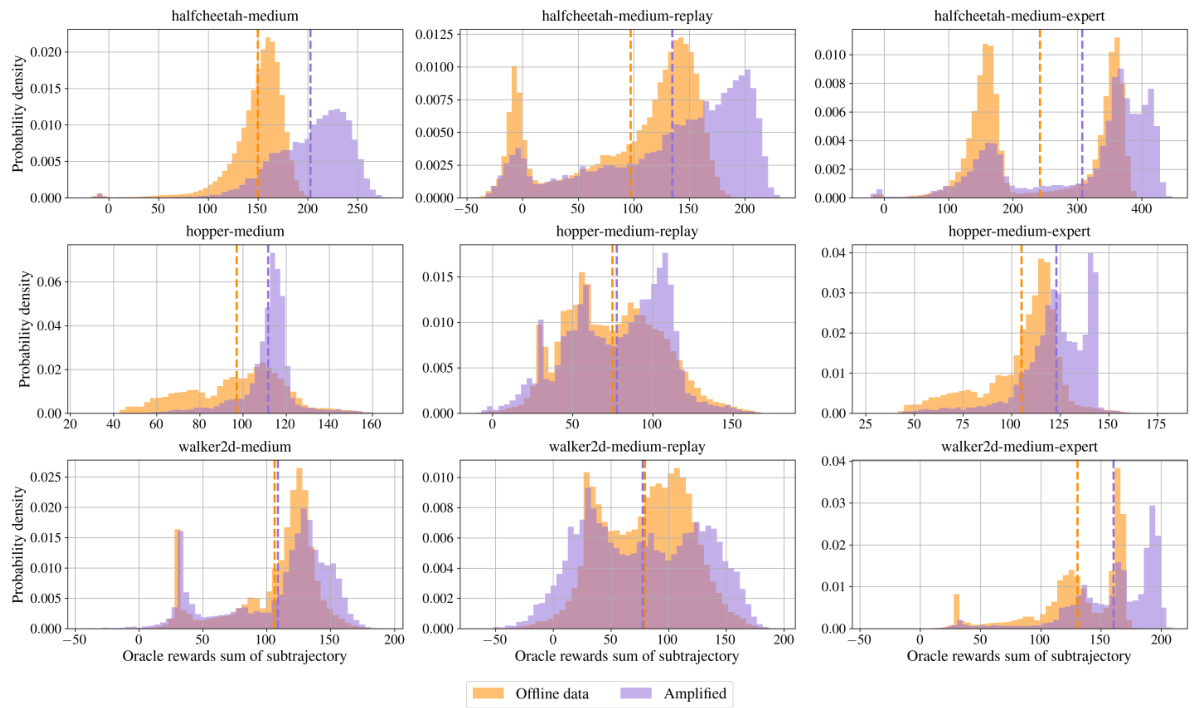
This table presents the D4RL normalized scores achieved by different offline RL algorithms (None, SynthER, GTA with μ=0.5 and α=1.3, GTA with μ=0.75 and α=1.3) on three locomotion tasks (Halfcheetah, Hopper, Walker2d) using medium and medium-replay datasets. The scores represent the average performance across multiple trials, along with standard deviations, indicating the variability in performance for each algorithm on each task and dataset.
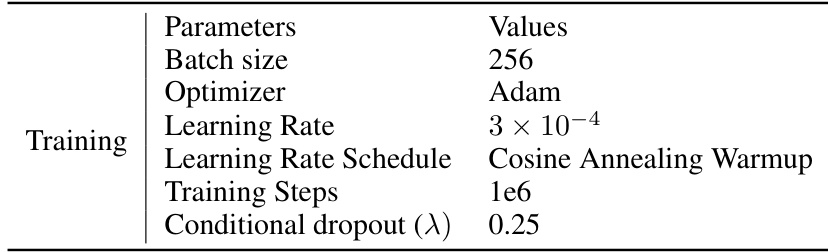
This table shows the hyperparameters used for training the backbone diffusion model in the Generative Trajectory Augmentation (GTA) method. It includes parameters such as batch size, optimizer (Adam), learning rate, learning rate schedule (Cosine Annealing Warmup), number of training steps, and conditional dropout rate. These settings are crucial for effectively training the diffusion model to generate high-quality trajectories.

This table lists the hyperparameters used for sampling trajectories from the diffusion model in the Generative Trajectory Augmentation (GTA) method. The hyperparameters are related to the Stochastic Differential Equation (SDE) sampler from the Elucidated Diffusion Model (EDM), including the number of diffusion steps, noise schedule parameters (σmin, σmax, Schurn, Smin, Smax, Snoise), and the guidance scale (w) for classifier-free guidance. These settings control aspects of the trajectory generation process, balancing exploration and exploitation.
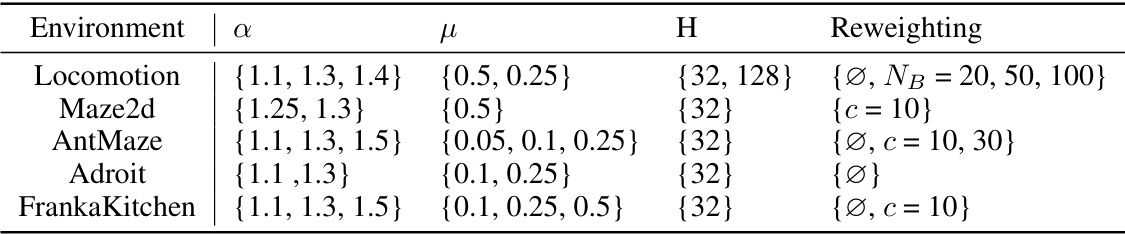
This table shows the hyperparameter search space used in the Generative Trajectory Augmentation (GTA) method. It lists the ranges of values explored for three key hyperparameters: α (guidance multiplier), μ (partial noising level), and H (horizon length) across different environments. The reweighting strategy used is also specified for each environment. The hyperparameter ranges reflect a balance between exploration and exploitation of the data during the augmentation process, with different ranges considered depending on task characteristics. This table is critical for understanding the experimental setup and how the algorithm was configured for different environments.
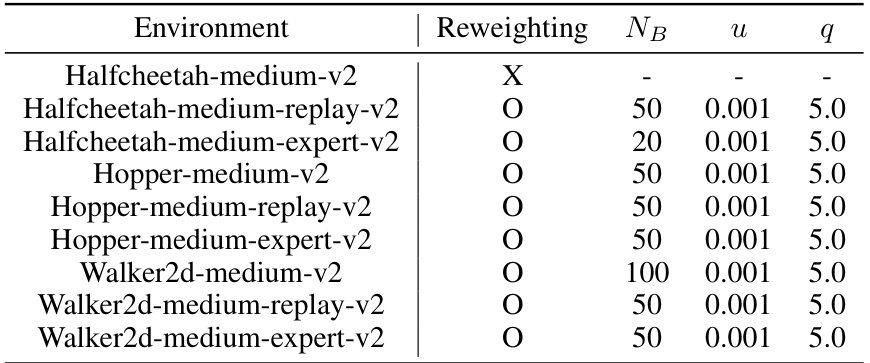
This table shows the hyperparameters used for reweighted sampling in different locomotion environments. Reweighting is applied to focus on high-rewarding regions in the dataset. The hyperparameters include whether reweighting is used (indicated by ‘O’ for yes and ‘X’ for no), the number of bins (NB) used for splitting the return, a smoothing parameter (u), and a parameter (q) that determines the weighting between high and low-score bins.

This table presents the results of ablation studies on the length of the horizon (H) used for trajectory-level generation in the GTA method. It shows the impact of varying H on both D4RL score and Dynamic MSE (dynamic mean squared error), a measure of how well the generated trajectories adhere to the environment dynamics. The results demonstrate the importance of using sequential relationships within transitions (H > 1) for effective data augmentation, as shorter horizons lead to a significant increase in dynamic MSE and a decrease in performance.
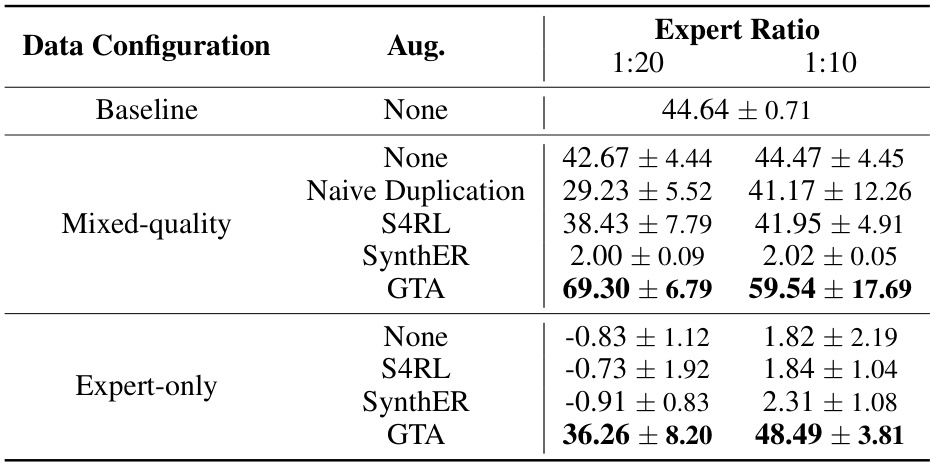
This table presents the results of the TD3BC algorithm on a sparse expert dataset. The performance is evaluated under various data augmentation techniques (None, Naive Duplication, S4RL, SynthER, GTA) using different ratios of expert to non-expert data (1:20 and 1:10). The results show that GTA significantly outperforms other methods and that even on a dataset of expert-only data, GTA provides a performance boost over other augmentation techniques. The experiment is done with 10 evaluation over 8 seeds.

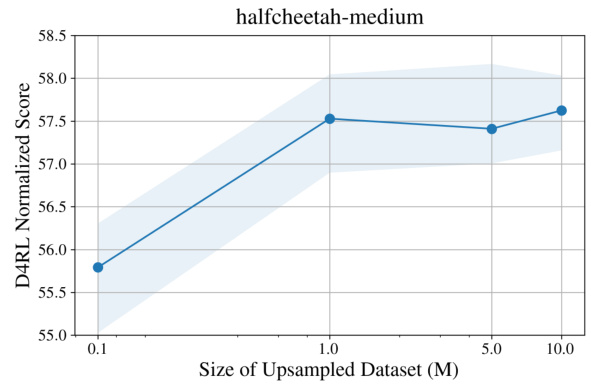
This table presents the D4RL scores obtained using the TD3BC algorithm with varying amounts of offline data (5%, 10%, 15%, 20%, and 100%). The results show the performance of TD3BC both with and without the proposed GTA augmentation method. The scores represent the mean and standard deviation across 10 evaluations with 4 random seeds for each data size. It demonstrates the sample efficiency of GTA when the size of the offline dataset is limited.

This table presents the results of experiments conducted on various Gym locomotion and maze tasks. The scores are normalized, meaning 0 represents a random policy and 100 an expert policy. The table compares the performance of different offline reinforcement learning (RL) algorithms, with and without data augmentation techniques. Each entry shows the mean and standard deviation of the normalized scores, averaged across 8 different random seeds. The bold entries highlight the highest scores achieved for each task and augmentation method.

This table presents the average scores achieved by the Decision Transformer algorithm on three different variations of the Maze2d environment from the D4RL benchmark dataset. The results are categorized by the augmentation method used (None, S4RL, GTA) and across three difficulty levels (umaze, medium, large). Each score represents the average performance over 100 evaluations with 4 random seeds, showcasing the impact of data augmentation on the performance of the Decision Transformer.

This table shows the ablation study result on reweighted sampling techniques. It shows the D4RL scores and oracle rewards with and without reweighted sampling on Hopper-medium-v2 and Walker2d-medium-v2 environments. The results indicate that reweighted sampling improves performance by increasing the D4RL scores and oracle rewards.

This table compares the performance of two different conditioning strategies for data augmentation using a diffusion model. The first strategy uses amplified return guidance as in the proposed GTA method, while the second uses amplified reward inpainting. The performance is measured using the D4RL score on three locomotion tasks: Halfcheetah-medium, Hopper-medium, and Walker2d-medium. The results show that amplified return guidance generally leads to higher D4RL scores compared to amplified reward inpainting, suggesting that the amplified return guidance approach is more effective in improving the performance of offline reinforcement learning algorithms.

This table presents the average performance results of different offline reinforcement learning algorithms on four complex robotics tasks: pen-human, door-human, FrankaKitchen-partial, and FrankaKitchen-complete. The algorithms tested include the baseline with no data augmentation (None), data augmentation using S4RL, SynthER, and the proposed GTA method. The highest average score for each task is highlighted in bold, and the mean and standard deviation are shown across 8 separate experimental runs (seeds). This allows for a comparison of the effectiveness of the data augmentation techniques on complex robotics tasks.

This table presents the results of experiments conducted on various Gym locomotion and maze tasks using different offline RL algorithms. The algorithms were tested with and without data augmentation techniques (None, S4RL, SynthER, and GTA). The table shows the normalized average scores achieved by each algorithm on each task, with the highest score for each task and augmentation method highlighted in bold. The scores represent the mean and standard deviation across 8 separate trials (seeds).

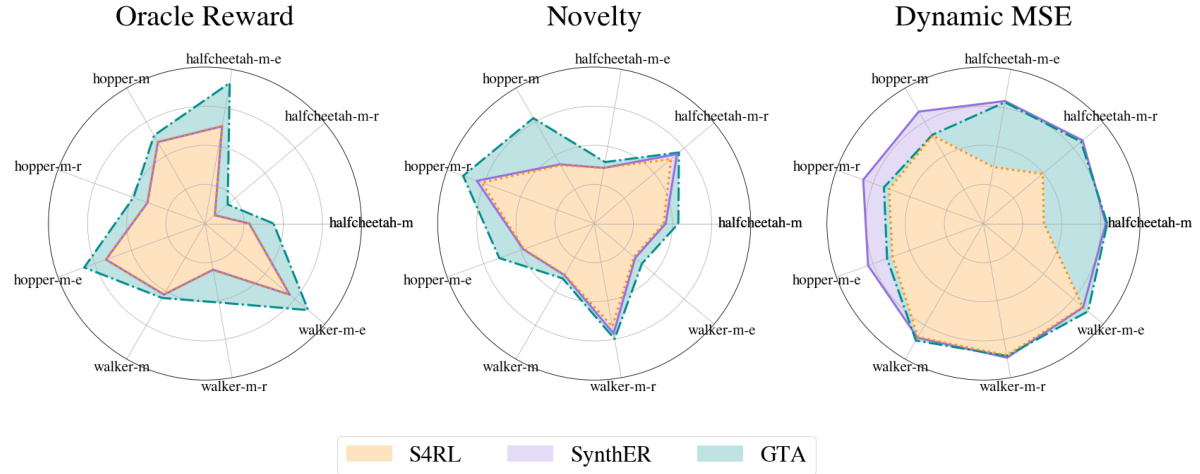
This table presents a comparison of data quality metrics for different conditioning strategies used in the generative trajectory augmentation process. The metrics include Dynamic Mean Squared Error (Dynamic MSE), which assesses the fidelity of the generated trajectories compared to real-world dynamics; Oracle reward, which measures the average reward of the generated trajectories; and Novelty, which quantifies the uniqueness of the generated trajectories compared to the original data. The table contrasts the performance of three methods: a baseline (no conditioning), a fixed conditioning strategy (conditioning on a constant reward value), an unconditioned strategy (no conditioning), and the proposed amplified return conditioning strategy (conditioning on an amplified reward value).
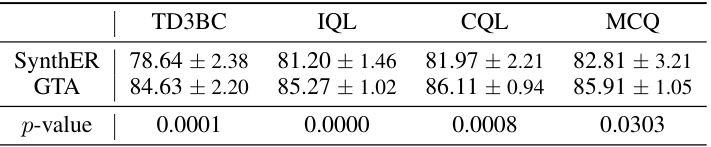
This table presents the results of Welch’s t-tests comparing the performance of GTA against SynthER across four different offline RL algorithms (TD3BC, IQL, CQL, and MCQ). The p-values indicate the statistical significance of the performance differences, with smaller p-values suggesting stronger evidence that GTA outperforms SynthER. All p-values are less than 0.05 indicating statistically significant improvement by GTA across all four algorithms.
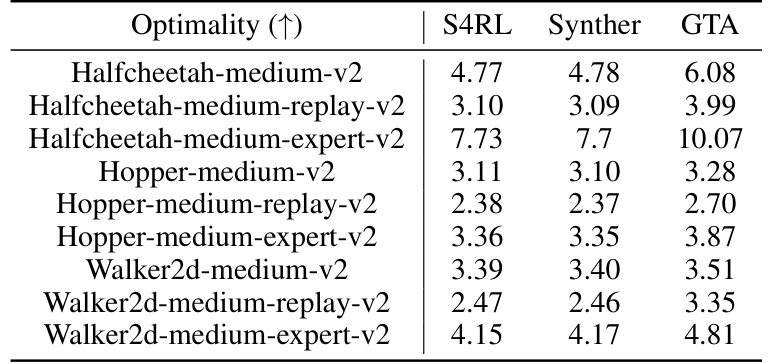
This table presents a quantitative comparison of the optimality achieved by three different data augmentation methods (S4RL, SynthER, and GTA) across various Gym locomotion tasks. Optimality is measured using the oracle reward, representing the average reward obtained by querying the environment with generated states and actions. The results show the average oracle reward for each method across several different tasks, providing insights into the effectiveness of each augmentation strategy in generating high-reward trajectories.
This table presents the results of experiments conducted on various Gym locomotion and maze tasks. The table shows the normalized average scores achieved by different offline reinforcement learning (RL) algorithms with and without data augmentation techniques (None, S4RL, SynthER, and GTA). Each cell contains the mean and standard deviation of the scores obtained across eight independent seeds. The highest scores for each task and algorithm are highlighted in bold, allowing for easy comparison of the performance of different methods.
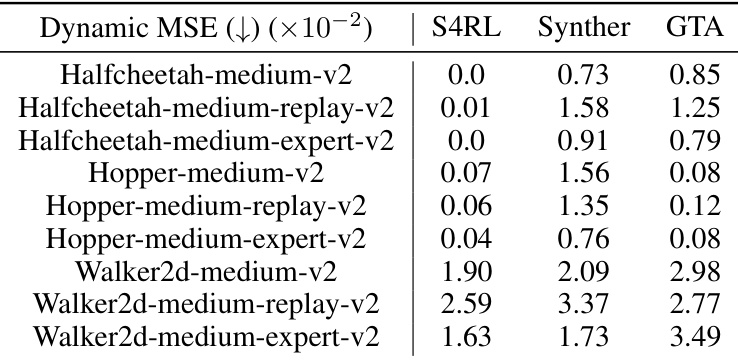
This table presents a comparison of the Dynamic Mean Squared Error (Dynamic MSE) across various gym locomotion tasks. Dynamic MSE is a metric used to assess the congruence of generated subtrajectories with the environment dynamics. Lower values indicate better agreement between generated and true dynamics. The table compares the Dynamic MSE for three different data augmentation methods: S4RL, SynthER, and GTA (the proposed method). The results are shown for different datasets, reflecting various difficulty levels in terms of data quality (medium, medium-replay, medium-expert).

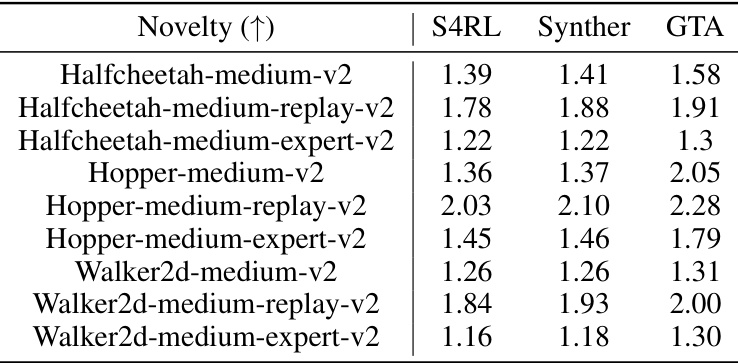
This table presents a comparison of novelty scores achieved by three different data augmentation methods (S4RL, SynthER, and GTA) across various gym locomotion tasks. Novelty, as a data quality metric, measures the uniqueness of the augmented trajectories compared to the original offline data. Higher novelty scores indicate that the augmentation method generated trajectories that are more distinct from the original data.
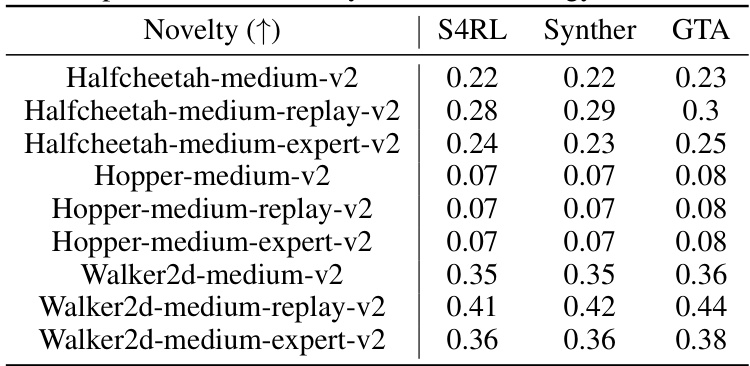
This table presents a comparison of the novelty scores achieved by three different data augmentation methods (S4RL, SynthER, and GTA) across various gym locomotion tasks. Novelty is a measure of how unique the generated trajectories are compared to the original dataset. The table shows the novelty scores for the state, action, and combined state-action for each augmentation method and task. Higher scores indicate greater novelty.
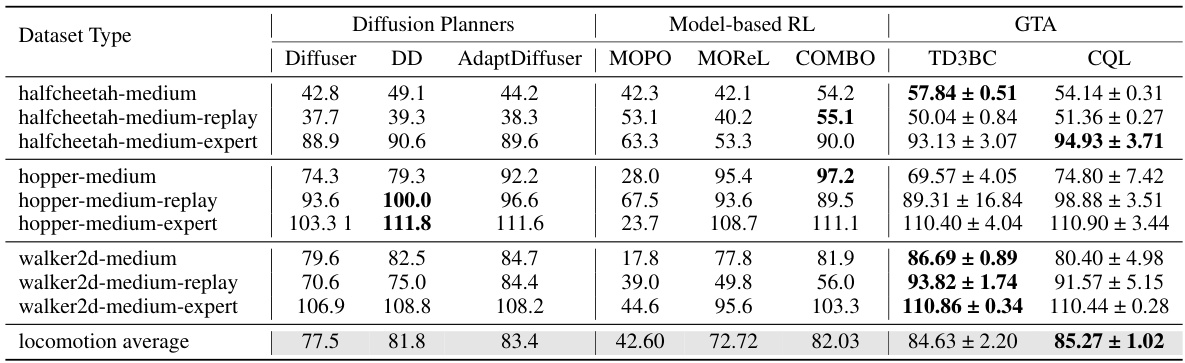
This table compares the performance of Generative Trajectory Augmentation (GTA) against several baseline methods, including diffusion planners (Diffuser, DD, AdaptDiffuser) and offline model-based RL algorithms (MOPO, MOREL, COMBO). The comparison is done across various locomotion tasks from the D4RL benchmark, showing the average normalized scores for each method. TD3BC and CQL are used as the offline RL algorithms in the GTA approach. The table highlights GTA’s superior performance compared to the baselines.

This table compares the computational cost of GTA against other methods (diffusion planners and model-based RL algorithms). It breaks down the time spent in each phase: model training, RL policy training, synthetic data generation, and policy evaluation. The results highlight GTA’s efficiency, especially in test-time evaluation.

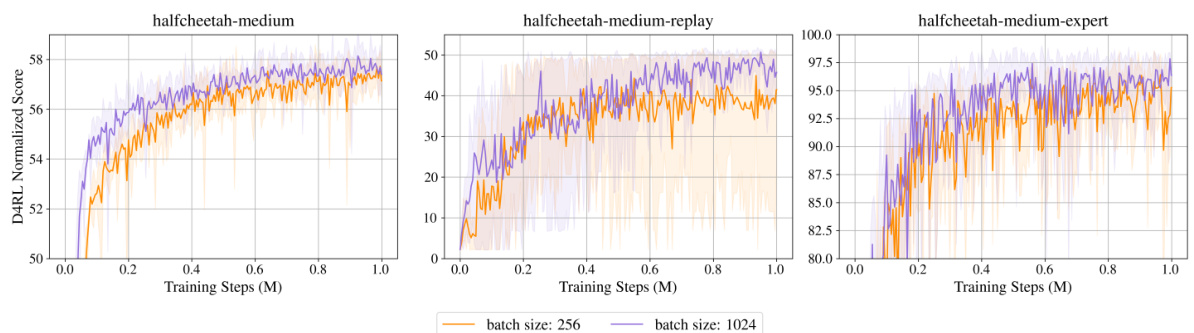
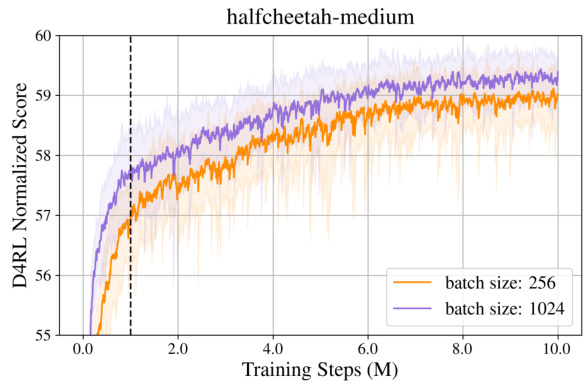
This table presents the results of training TD3BC, CQL, and IQL algorithms on D4RL MuJoCo locomotion tasks using different batch sizes (256 and 1024). It compares the performance (normalized average scores) across various datasets (medium, medium-replay, medium-expert) for each algorithm and batch size. The results show that increasing the batch size doesn’t significantly impact performance when there’s no data augmentation.

This table presents the results of experiments conducted to assess the impact of varying batch sizes on the performance of different offline reinforcement learning algorithms. The experiments were performed on the D4RL MuJoCo locomotion tasks using TD3BC, CQL, and IQL algorithms with batch sizes of 256 and 1024. The results indicate that increasing the batch size does not significantly affect the performance when no modifications are made to the offline dataset. The table is structured to show the average normalized scores for each algorithm and batch size across different tasks (Halfcheetah, Hopper, and Walker2d) with different data qualities (medium, medium-replay, and medium-expert).
Full paper#