TL;DR#
Traditional reinforcement learning (RL) algorithms often struggle with learning complex policies due to limitations in representing multimodal distributions. This paper addresses this issue by proposing Diffusion Actor-Critic with Entropy Regulator (DACER), a novel algorithm that leverages the power of diffusion models to enhance the representational capacity of the policy. Existing methods using simple Gaussian distributions fail to capture the multimodality of optimal policies, leading to suboptimal performance.
DACER addresses this by conceptualizing the reverse process of a diffusion model as a novel policy function. This allows the algorithm to effectively model multimodal action distributions. Since the diffusion policy’s entropy lacks an analytical expression, the paper proposes a method to estimate it using Gaussian Mixture Models (GMM). This estimated entropy is then used to adaptively regulate the exploration and exploitation balance, thereby improving performance. The algorithm’s efficacy is demonstrated through experiments on MuJoCo benchmarks, showing state-of-the-art performance and superior representational capacity.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel online reinforcement learning algorithm that overcomes limitations of traditional methods. By using diffusion models, it enables the learning of more complex policies and improves performance. The adaptive adjustment of exploration-exploitation via entropy estimation is a significant contribution, opening avenues for further research in this area. The open-sourcing of the code further enhances its impact.
Visual Insights#
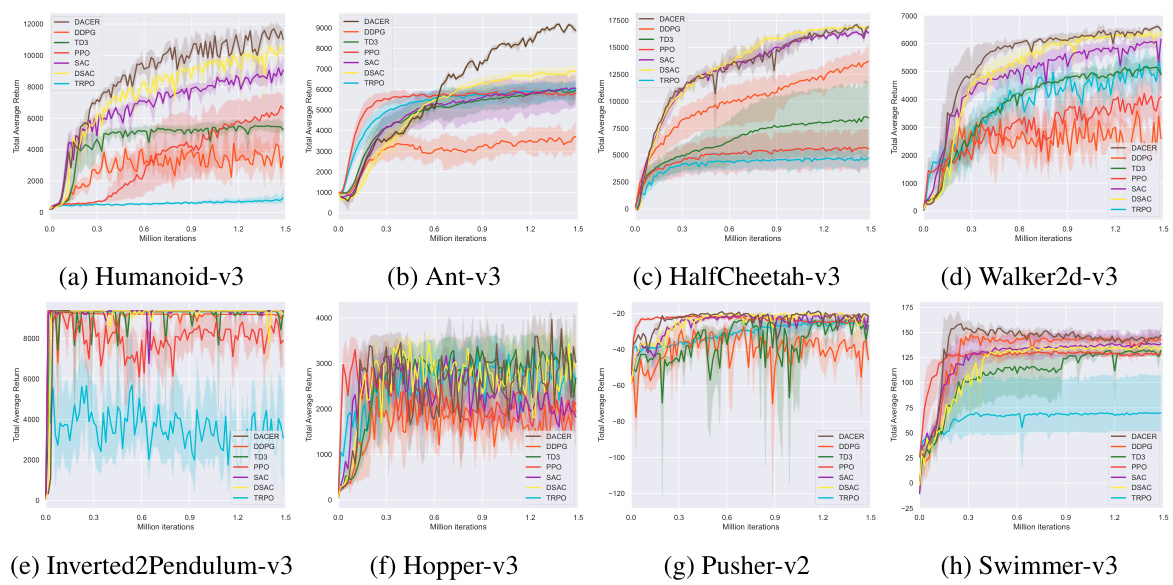
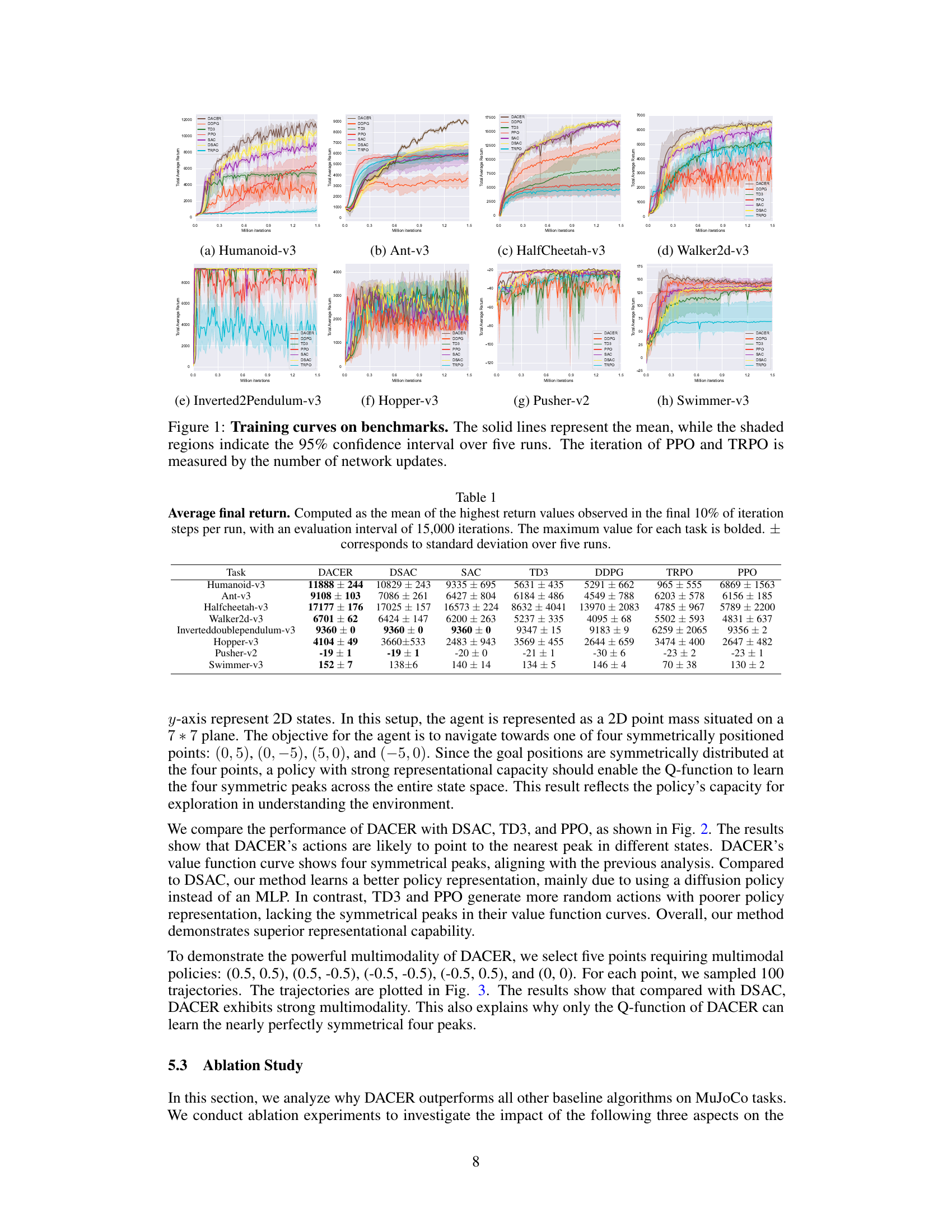
🔼 This figure displays the training curves for eight different MuJoCo control tasks across eight reinforcement learning algorithms: DACER, DDPG, TD3, PPO, SAC, DSAC, and TRPO. The x-axis represents the number of iterations (or network updates for PPO and TRPO), and the y-axis represents the average return achieved by each algorithm. Shaded regions around the mean curves show the 95% confidence intervals based on five separate training runs, illustrating the variability in performance. The plot allows for a direct comparison of the learning progress and overall performance of DACER against other state-of-the-art algorithms.
read the caption
Figure 1: Training curves on benchmarks. The solid lines represent the mean, while the shaded regions indicate the 95% confidence interval over five runs. The iteration of PPO and TRPO is measured by the number of network updates.

🔼 This table presents the average final return achieved by different reinforcement learning algorithms across various MuJoCo benchmark tasks. The average is calculated from the highest return values observed during the final 10% of the training process, evaluated every 15,000 iterations. The results represent the mean and standard deviation across five independent runs, providing a measure of algorithm performance and its stability.
read the caption
Table 1 Average final return. Computed as the mean of the highest return values observed in the final 10% of iteration steps per run, with an evaluation interval of 15,000 iterations. ± corresponds to standard deviation over five runs.
In-depth insights#
Diffusion Policy RL#
Diffusion Policy RL represents a novel approach in reinforcement learning that leverages the power of diffusion models for policy representation. Instead of traditional parametric policies, such as Gaussian distributions, diffusion models offer the potential to model complex, multimodal action distributions more effectively. This is crucial because optimal policies in many real-world scenarios may exhibit multimodality, which is difficult for standard methods to capture. The core idea is to frame the reverse diffusion process as a policy function. This allows the agent to learn a policy that can generate actions from noise, effectively sampling from a complex probability distribution. However, estimating the entropy of such a policy, which is vital for balancing exploration and exploitation, presents a challenge, often requiring novel approximation techniques. The success of Diffusion Policy RL heavily relies on effective entropy estimation methods and the ability of the underlying diffusion model to accurately learn the desired policy distribution from interaction with the environment. Furthermore, efficient training methods are essential for practical applications, demanding careful consideration of computational cost and algorithmic stability.
Entropy Regulation#
Entropy regulation in reinforcement learning aims to balance exploration and exploitation. High entropy encourages exploration, allowing the agent to discover diverse actions and states, potentially leading to better long-term performance. Low entropy prioritizes exploitation, focusing on actions that have yielded high rewards in the past. The challenge lies in finding the optimal balance, as too much exploration can lead to instability and poor performance, while too much exploitation may trap the agent in local optima. Effective entropy regulation methods often adapt to the learning process, increasing exploration in early stages and gradually shifting to exploitation as the agent gains knowledge. This adaptive approach is crucial for navigating the exploration-exploitation dilemma effectively. Estimating the entropy of a policy is often a key component, enabling informed control of exploration-exploitation trade-offs. Techniques like temperature scaling and parameterized entropy bonuses provide mechanisms to adjust the entropy level, offering flexibility in tuning the balance during learning. The ultimate goal of entropy regulation is to enhance learning efficiency and achieve robust optimal policies.
Multimodal Policy#
A multimodal policy in reinforcement learning aims to address the limitations of traditional policies, such as diagonal Gaussian distributions, which struggle to represent complex, multi-modal action spaces. Multimodal policies are crucial when optimal actions exhibit multiple distinct patterns within a single state, reflecting different ways to achieve a similar goal or navigating diverse situations. This necessitates a policy representation capable of capturing these multiple modes, rather than simply averaging them or selecting a single dominant one. The core challenge lies in finding a suitable function approximator that can effectively learn and represent these multiple peaks in the action-value landscape. Approaches such as diffusion models, Gaussian Mixture Models, or mixture density networks offer promising avenues to create flexible and expressive policy representations, enabling better exploration and exploitation of the action space and ultimately leading to improved performance in complex decision-making tasks. However, training such multimodal policies often presents significant computational challenges and requires careful consideration of exploration-exploitation trade-offs, often necessitating sophisticated entropy regularization techniques.
GMM Entropy Est.#
The heading ‘GMM Entropy Est.’ suggests a method for estimating the entropy of a probability distribution using Gaussian Mixture Models (GMMs). This is a crucial step because the entropy of a diffusion model’s policy is not analytically tractable, hindering the use of entropy-maximizing reinforcement learning techniques. GMMs are employed due to their capacity to approximate complex, multimodal distributions, a characteristic often exhibited by optimal policies. The method likely involves fitting a GMM to a set of samples from the diffusion policy and then using the parameters of the fitted GMM to calculate an approximation of the entropy. The accuracy of this estimation is critical, as an inaccurate entropy estimate can lead to poor exploration-exploitation trade-offs and suboptimal policy performance. Computational cost and convergence speed of the GMM fitting process are also important considerations. This approach allows the incorporation of entropy regularization into the training process, potentially improving the performance of the reinforcement learning algorithm by encouraging exploration and mitigating the risk of converging to suboptimal local optima.
Future Works#
Future research directions stemming from this work could explore more sophisticated entropy estimation techniques beyond Gaussian Mixture Models (GMMs) to better capture the true entropy of the diffusion policy, leading to more robust exploration-exploitation balance. Investigating alternative diffusion model architectures and training strategies, such as improved denoising schedules or different generative models, could enhance the policy’s representational power and sample efficiency. A significant area for future work is to apply the DACER framework to a wider range of complex control tasks, including those with high-dimensional state or action spaces, to further evaluate its generalization capabilities and address challenges posed by real-world scenarios. Finally, exploring hybrid approaches that combine the strengths of diffusion models with other policy representation methods, such as neural networks or Gaussian processes, may provide further improvements in performance and robustness.
More visual insights#
More on figures
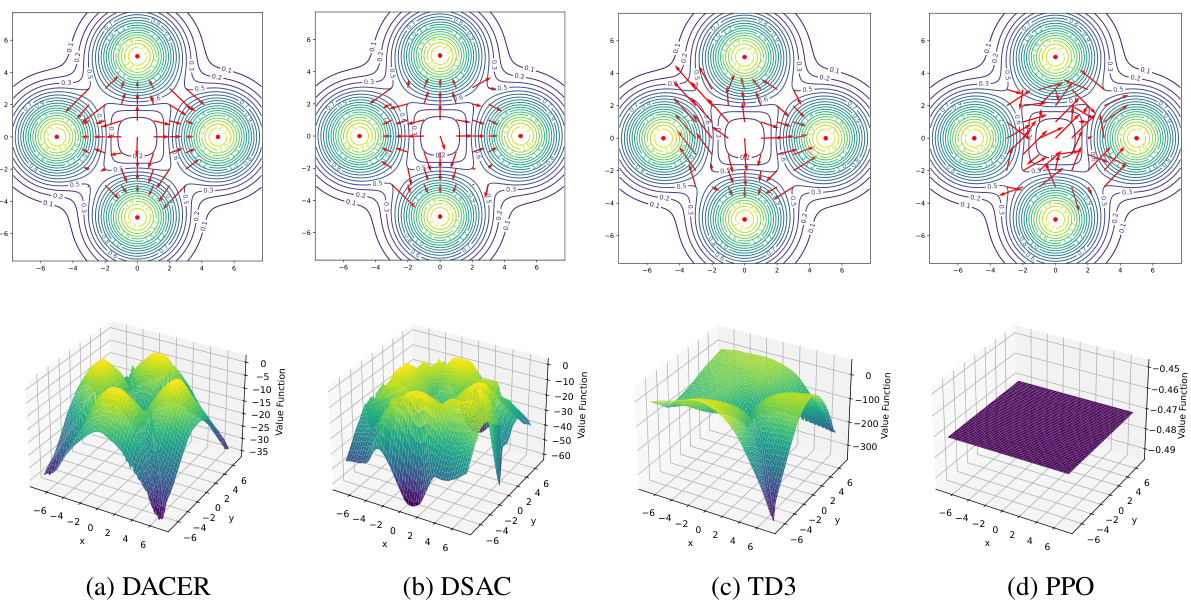
🔼 This figure compares the policy representation of four different reinforcement learning algorithms (DACER, DSAC, TD3, and PPO) in a multimodal environment. The top row displays a visualization of the learned policy distributions for each algorithm. The length and direction of the red arrows represent the magnitude and direction of the actions predicted by the policy for each state. The bottom row shows 3D surface plots representing the Q-value function (value function) for each algorithm. These plots visualize how the algorithms learn to value different states and actions. The multimodal nature of the environment is evident in the multiple peaks in the Q-value functions of successful algorithms (DACER and DSAC). Algorithms like TD3 and PPO show flatter Q-value functions indicating less ability to discriminate between states and actions in the multimodal environment.
read the caption
Figure 2: Policy representation comparison of different policies on a multimodal environment. The first row exhibits the policy distribution. The length of the red arrowheads denotes the size of the action vector, and the direction of the red arrowheads denotes the direction of actions. The second row shows the value function of each state point.
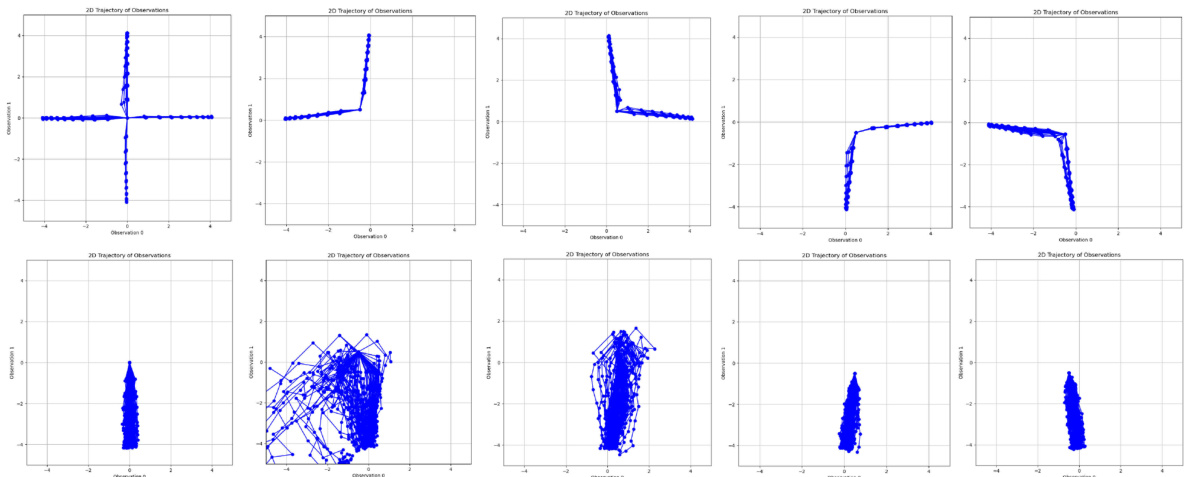
🔼 This figure compares the experimental results of DACER and DSAC on a multi-goal environment. Five points were selected that demand multimodal policies. For each point, 100 trajectories were sampled and plotted to show the trajectory distribution. The figure aims to visually demonstrate the superior multimodal capabilities of the DACER algorithm compared to DSAC by showing distinct trajectory clusters corresponding to different goal locations.
read the caption
Figure 3: Multi-goal multimodal experiments. We selected 5 points that require multimodal policies: (0, 0), (−0.5, 0.5), (0.5, 0.5), (0.5, −0.5), (−0.5, −0.5), and sampled 100 trajectories for each point. The top row shows the experimental results of DACER, another shows the experimental results of DSAC.
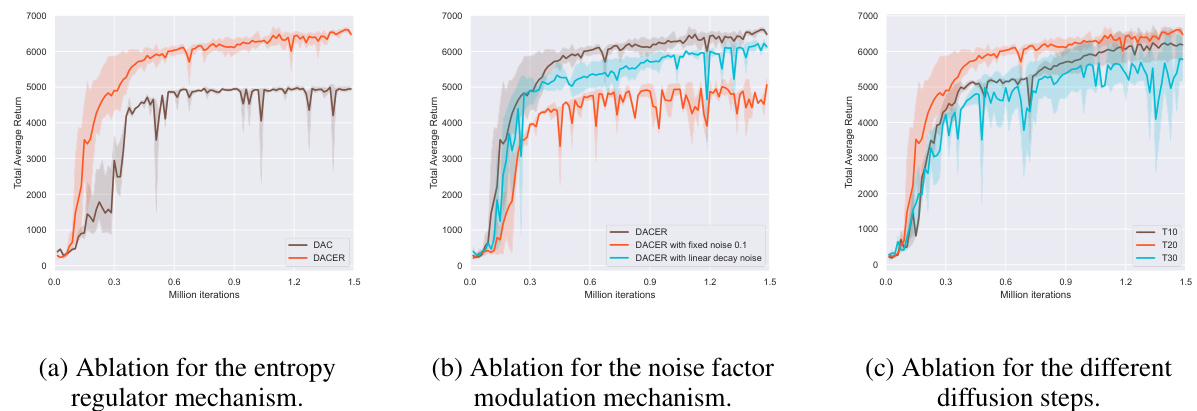
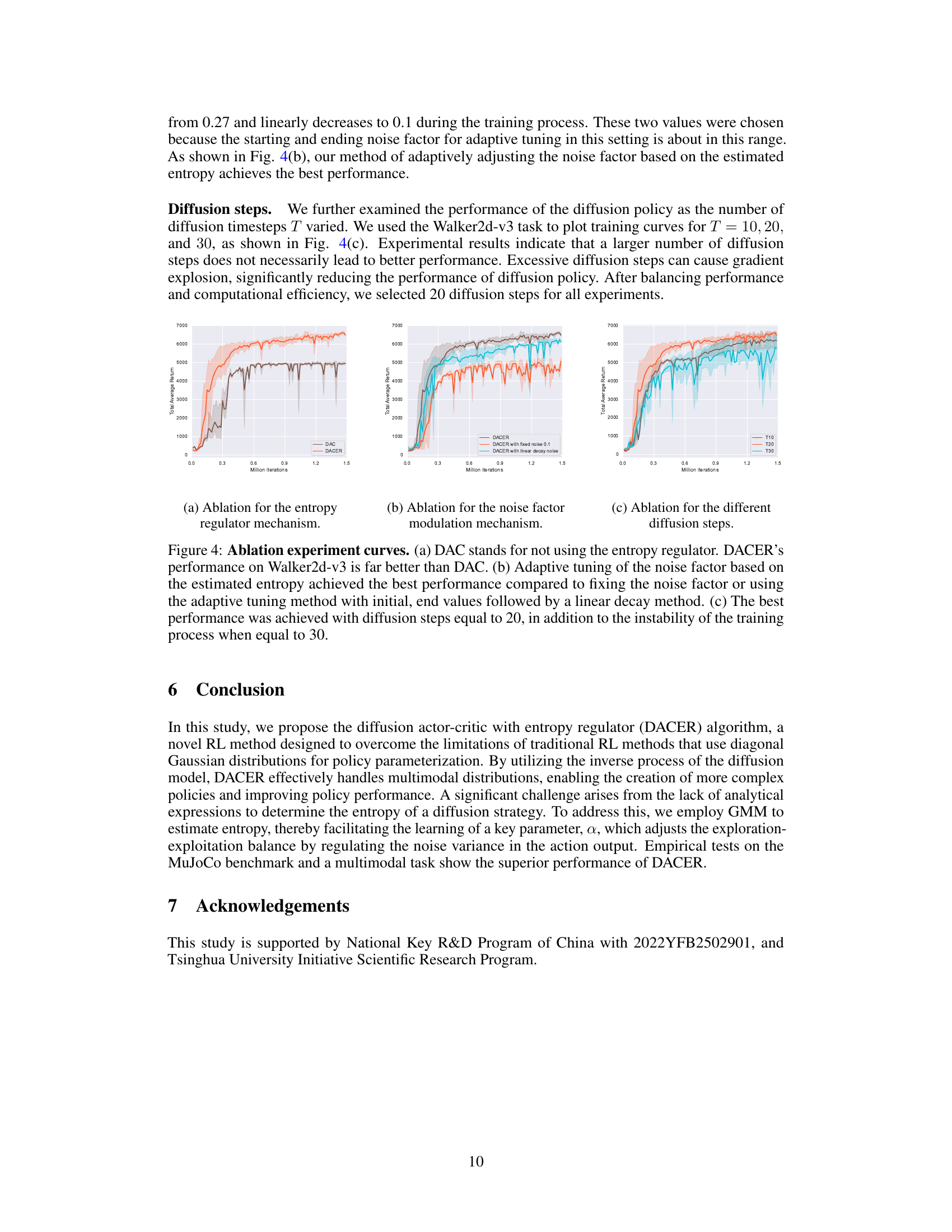
🔼 This figure displays the training curves for various reinforcement learning algorithms across multiple MuJoCo benchmark tasks. The curves show the average total reward obtained over multiple runs. Shaded areas represent the 95% confidence interval, illustrating the variability in performance. The x-axis represents the number of training iterations, while the y-axis represents the total average return. Different colors represent different algorithms being compared.
read the caption
Figure 1: Training curves on benchmarks. The solid lines represent the mean, while the shaded regions indicate the 95% confidence interval over five runs. The iteration of PPO and TRPO is measured by the number of network updates.
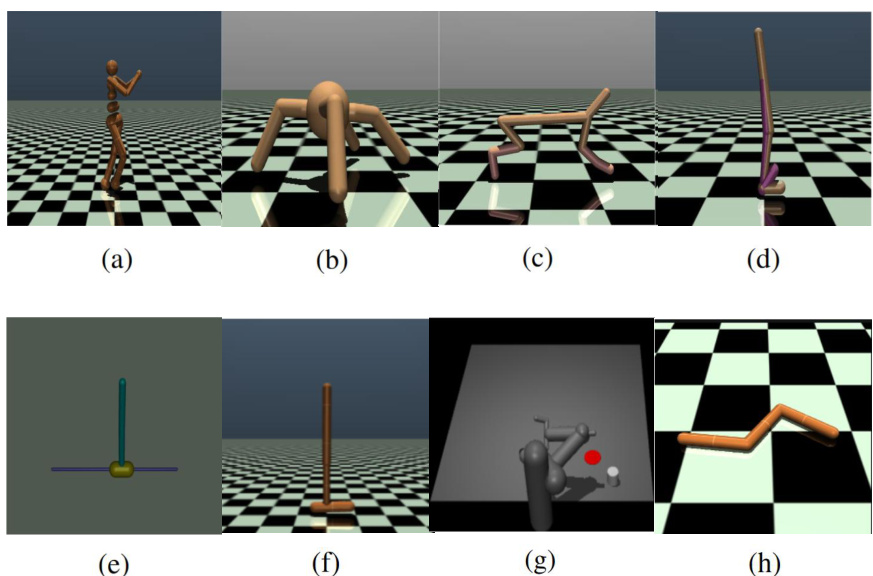
🔼 This figure shows eight different simulated environments used in the MuJoCo benchmark for evaluating reinforcement learning algorithms. Each subfigure displays a visual representation of one task and specifies the dimensionality of its state space (s) and action space (a), indicating the complexity of each environment.
read the caption
Figure 5: Simulation tasks. (a) Humanoid-v3: (s × a) ∈ R376 × R17. (b) Ant-v3: (s × a) ∈ R111 × R8. (c) HalfCheetah-v3 : (s × a) ∈ R17 × R6. (d) Walker2d-v3: (s × a) ∈ R17 × R6. (e) InvertedDoublePendulum-v3: (s × a) ∈ R6 × R¹. (f) Hopper-v3: (s × a) ∈ R11 × R³. (g) Pusher-v2: (s × a) ∈ R23 × R7. (h) Swimmer-v3: (s × a) ∈ R8 × R2.
More on tables

🔼 This table lists the hyperparameters used in the experiments. It is divided into shared hyperparameters (common across all algorithms) and algorithm-specific hyperparameters. Shared hyperparameters include replay buffer capacity, batch size, initial alpha, action bounds, hidden layer structure of the actor and critic networks, activation functions, optimizer, learning rates, discount factor, reward scaling, and more. Algorithm-specific hyperparameters include those specific to the maximum-entropy framework, such as the expected entropy and the deterministic policy.
read the caption
TABLE 2 DETAILED HYPERPARAMETERS.
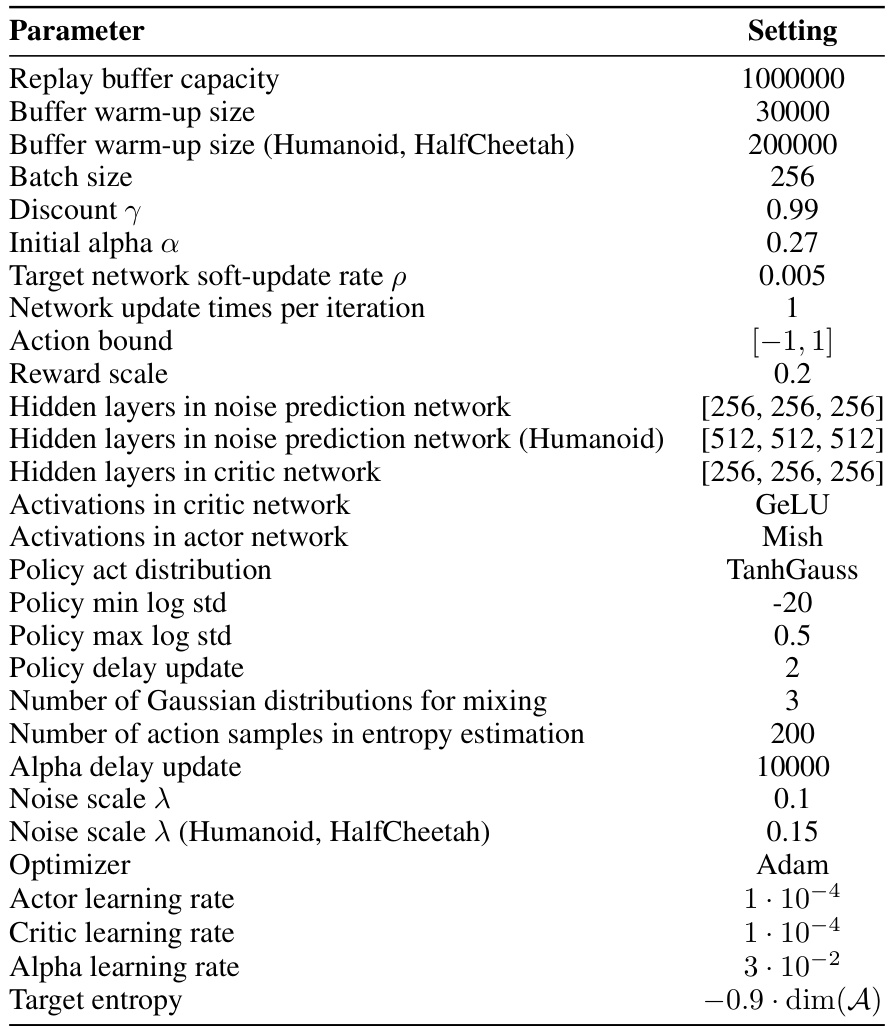
🔼 This table lists the hyperparameters used in the DACER algorithm. It includes settings for replay buffer capacity, batch size, discount factor, learning rates for actor, critic, and alpha, and other parameters related to the diffusion model such as noise scale and the number of Gaussian distributions used for mixing.
read the caption
TABLE 3 ALGORITHM HYPERPARAMETER
Full paper#