↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
The Schrödinger Bridge (SB) problem offers a powerful framework for generative modeling. However, existing methods like Iterative Markovian Fitting (IMF) suffer from long inference times due to the use of continuous-time stochastic processes. This necessitates numerical solvers with many steps, limiting efficiency.
This research proposes a novel approach using Discrete-time IMF (D-IMF). This method replaces the learning of continuous-time stochastic processes with learning a few transition probabilities in discrete time. D-IMF is naturally implemented using Denoising Diffusion GANs (DD-GANs), achieving efficiency. The method also delivers closed-form update formulas for high-dimensional Gaussian distributions, improving understanding.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on generative models and optimal transport. It significantly accelerates inference time in Schrödinger Bridge problems, a major bottleneck in current approaches. The proposed method, using a novel discrete-time approach and DD-GANs, opens new avenues for research in high-resolution image translation and other generative tasks. Its practical implementation and theoretical analysis provide a solid foundation for future work.
Visual Insights#

This figure demonstrates the efficiency of the proposed Discrete-time Iterative Markovian Fitting (D-IMF) approach for unpaired image-to-image translation. The top row shows the D-IMF method, translating a male face image into a female face image in only four steps. The bottom row shows the Iterative Markovian Fitting (IMF) method, which requires significantly more steps (~80) to achieve a comparable result. Both methods use the CelebA dataset, specifically male to female face images with a resolution of 128x128 pixels. The D-IMF approach’s speed advantage is a key finding of the paper.

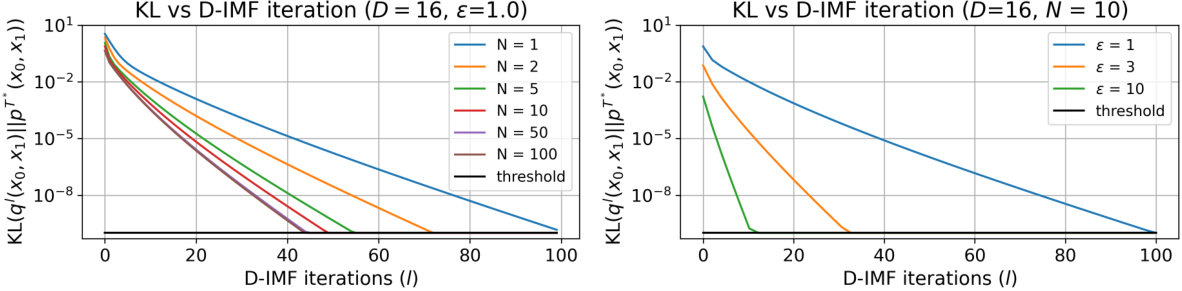
This table presents a comparison of the CBW2-UVP metric for different algorithms on the Schrödinger Bridge (SB) benchmark. The CBW2-UVP metric measures the difference between the learned solution and the ground truth static SB solution. Lower values indicate better performance. The table compares the ASBM algorithm to other methods (DSBM and SF2M-Sink Bridge matching), with the best-performing algorithm for each setup highlighted. It provides results for various dimensions (D) and epsilon (ε) values.
In-depth insights#
Adversarial SB Matching#
The heading “Adversarial SB Matching” suggests a novel approach to solving the Schrödinger Bridge (SB) problem using adversarial techniques. The SB problem, rooted in optimal transport theory, seeks to find the most probable stochastic process connecting two probability distributions. This adversarial approach likely improves efficiency by replacing computationally expensive numerical solvers for stochastic differential equations, commonly used in traditional SB solutions, with a more efficient adversarial training process. The “Adversarial” component suggests a Generative Adversarial Network (GAN)-based framework, where a generator proposes stochastic processes, and a discriminator evaluates their probability. This adversarial setup could lead to faster convergence and better solutions compared to traditional iterative methods. The combination of optimal transport (implied by SB) and adversarial training offers a potent method for generative modeling and potentially for other applications demanding efficient interpolation between probability distributions. The method might involve discrete time steps for easier implementation and training, offering a practical advantage over continuous-time approaches. The overall success hinges on the ability to effectively train the adversarial network, overcoming the challenges associated with GAN training, such as mode collapse and instability.
D-IMF Algorithm#
The core of the proposed approach lies in the novel D-IMF algorithm, a discrete-time counterpart to the Iterative Markovian Fitting (IMF) method. D-IMF significantly accelerates inference by replacing the computationally expensive continuous-time stochastic differential equation solvers of IMF with the learning of a few transition probabilities in discrete time. This simplification enables the use of readily available and efficient adversarial generative modeling techniques, such as Denoising Diffusion GANs (DD-GANs), for practical implementation. The algorithm elegantly alternates between discrete Markovian and reciprocal projections, iteratively refining the learned transition probabilities to achieve a high-quality approximation of the optimal transport plan. The key advantage is drastically reduced computational cost, allowing for significantly faster inference with comparable results to the more complex continuous-time counterpart. This efficiency gain is critical, especially for applications involving high-dimensional data, where traditional optimal transport methods can become computationally prohibitive. The theoretical underpinnings of D-IMF are rigorously established, with proofs demonstrating its convergence to the Schrödinger Bridge solution. The efficiency improvements and the theoretical foundation of D-IMF are significant contributions to the field of generative modeling and optimal transport.
Gaussian Analysis#
A Gaussian analysis within a research paper would likely involve exploring the properties of Gaussian distributions and their applications to the specific problem at hand. This might include using Gaussian processes for modeling, applying Gaussian mixture models for clustering or classification, or leveraging the central limit theorem to justify using normal approximations. The core of the analysis would depend heavily on whether the data or variables being studied are, or can be reasonably approximated as, Gaussian. If so, powerful statistical techniques tailored to Gaussian distributions could be applied. However, if the data are non-Gaussian, transformations or alternative modeling methods would likely need to be considered to effectively utilize a Gaussian approach. A key aspect of the analysis would involve assessing the validity of the Gaussian assumption, potentially using graphical methods like Q-Q plots or statistical tests of normality. The analysis would also likely include a discussion of how the Gaussian assumption impacts the interpretation of the results and the reliability of any statistical inferences made.
Image Translation#
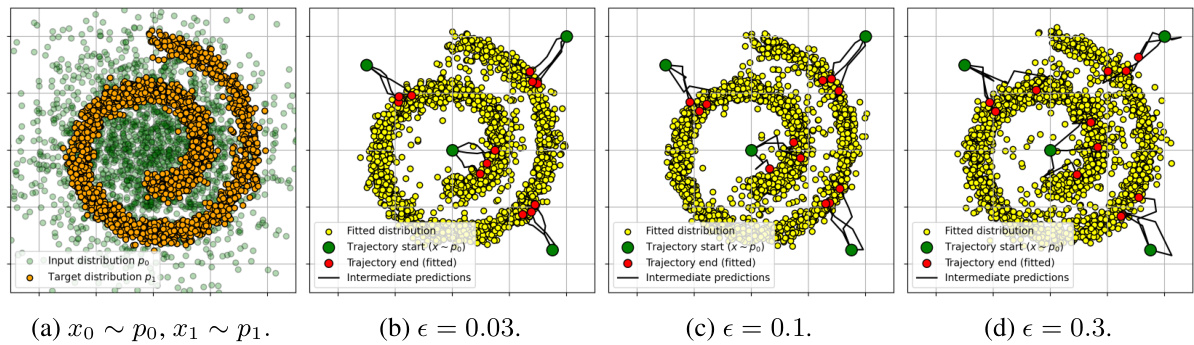
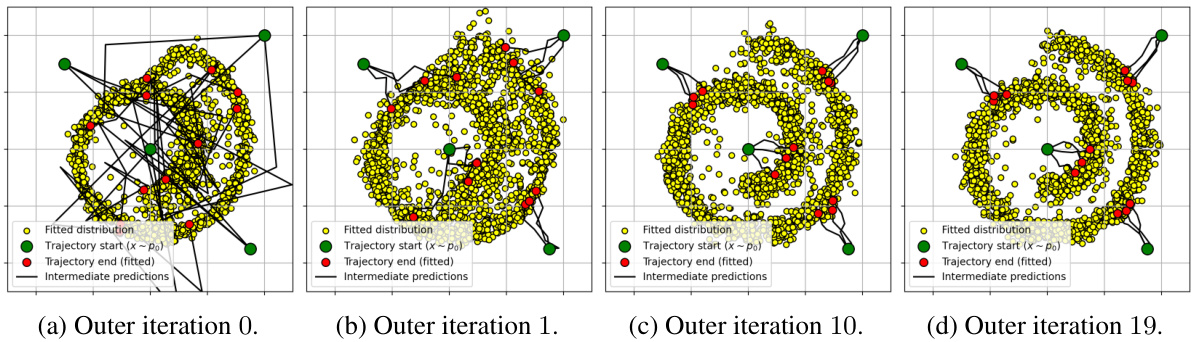
Image translation, in the context of this research paper, likely refers to the task of transforming images from one domain to another. This could involve translating images of faces from a male-to-female representation or vice versa, or it could entail other types of image-to-image translations. The core idea is to learn a mapping between the source and target domains, enabling the generation of realistic and high-quality translated images. The success of this process relies heavily on the effectiveness of the underlying model in capturing the intricate features and patterns of both domains. A key challenge is handling the problem of unpaired data, which is a situation where source and target images are not directly associated. The authors likely present a novel method to address this challenge, potentially leveraging adversarial learning or other advanced techniques. A key focus might be on enhancing the speed and efficiency of the translation process, achieving high-quality results with fewer computational steps. The evaluation metrics will likely include measures like Fréchet Inception Distance (FID) and Learned Perceptual Image Patch Similarity (LPIPS), indicating the quality and realism of translated images. Therefore, image translation in this paper is likely a sophisticated research topic concerning computational efficiency and data representation.
Future Directions#
Future research directions stemming from this work could explore extending the D-IMF framework to handle more complex data distributions and higher-dimensional spaces. The current implementation relies on Gaussian assumptions, limiting its applicability. Investigating alternative projection methods beyond the Markovian and reciprocal projections used here could enhance performance and potentially lead to new theoretical insights into the Schrödinger Bridge problem. Furthermore, exploring connections between D-IMF and other generative models such as normalizing flows or score-based models may yield hybrid approaches that combine the strengths of different techniques. The current empirical results show promise; however, a more thorough theoretical analysis of the convergence rate and stability of the D-IMF algorithm is necessary. Finally, exploring the practical implications of ASBM in various applications (e.g., image synthesis, style transfer, and domain adaptation) is essential to fully assess its potential impact.
More visual insights#
More on figures
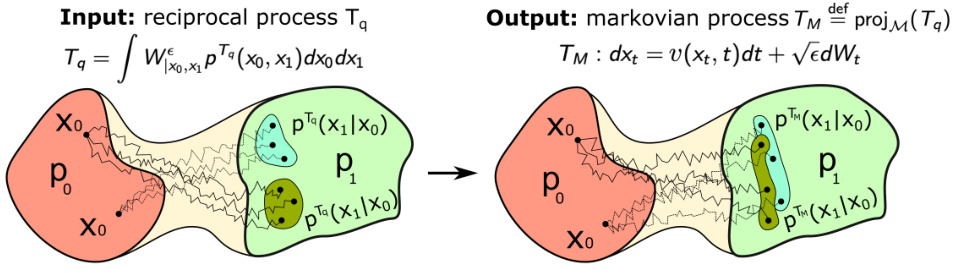
This figure illustrates the Markovian projection of a reciprocal stochastic process. The input is a reciprocal process Tq, which is a mixture of Brownian bridges. The Markovian projection aims to find a Markovian process TM that is closest to Tq in terms of Kullback-Leibler (KL) divergence. The output is a Markovian process TM defined by a stochastic differential equation (SDE) with drift v(xt, t). The figure visually represents how the Markovian projection transforms the reciprocal process into a Markovian process while preserving the marginal distributions at the start and end times (t=0, 1).

This figure demonstrates the effectiveness of the proposed Discrete-time Iterative Markovian Fitting (D-IMF) approach for unpaired image-to-image translation. It shows an example of translating male faces to female faces using the CelebA dataset. The left side displays the input images, and the right shows the results after only four function evaluations (NFEs) using the D-IMF method. The middle portion illustrates the intermediate steps of the process. The authors highlight that the quality of the results is comparable to those achieved by the conventional Iterative Markovian Fitting (IMF) method, which requires hundreds of steps.

This figure illustrates the reciprocal projection of a discrete stochastic process. The input is a discrete process q with a joint distribution q(x0, x1) at times t=0 and t=1. The reciprocal projection inserts a discrete Brownian bridge pW(Xt1,…,Xtv|x0,x1) between the start and end points, resulting in a new discrete stochastic process r with the same marginal distribution q(x0,x1) at times t=0 and t=1. The Brownian bridge is a Wiener process conditioned on the start and end points.

This figure illustrates the Markovian projection of a reciprocal discrete stochastic process. The input is a reciprocal process, represented as a distribution q with start and end points (x0 and x1) and intermediate points (Xin). The projection projects this process onto the space of Markovian processes, resulting in a Markovian process m which still maintains the same marginal distributions. The key difference is the stochastic dependencies between the intermediate points, which are independent of past and future points in the Markovian projection.
This figure shows a comparison between the proposed Discrete-time Iterative Markovian Fitting (D-IMF) method and the existing Iterative Markovian Fitting (IMF) method for unpaired image-to-image translation. The D-IMF method achieves comparable results to the IMF method but uses significantly fewer steps (4 vs. 100). The input images are from the CelebA dataset, specifically male and female faces at a resolution of 128x128 pixels. The results demonstrate that the D-IMF method is efficient in performing image translation.

This figure shows a comparison of image-to-image translation results using two different approaches: the proposed Discrete-time Iterative Markovian Fitting (D-IMF) and the existing Iterative Markovian Fitting (IMF). The input is a set of male faces from the CelebA dataset. The D-IMF approach translates these into female faces using only 4 function evaluations (NFEs), while the IMF method requires 100 NFEs to achieve comparable results. The figure visually demonstrates the efficiency of the D-IMF approach in generating high-quality results with significantly fewer computational steps. The images are 128x128 pixels.
This figure shows a comparison of image-to-image translation results using two different approaches: the proposed Discrete-time Iterative Markovian Fitting (D-IMF) method and the existing Iterative Markovian Fitting (IMF) method. The input images are from the CelebA dataset, specifically male faces which the model translates to female faces. The D-IMF method achieves comparable results to the IMF method but using only 4 steps instead of the 100 steps required by the IMF approach, showcasing its efficiency in terms of inference time.
This figure shows a comparison of unpaired image-to-image translation results using two different methods: the proposed Discrete-time Iterative Markovian Fitting (D-IMF) approach and the Iterative Markovian Fitting (IMF) method. The input images are shown on the left, and the output images produced by each method after a specified number of steps are displayed. D-IMF achieves comparable results to IMF but with significantly fewer steps (4 steps versus approximately 80 steps). This highlights the efficiency of the proposed D-IMF approach.

This figure shows the results of unpaired image-to-image translation using the proposed Discrete-time Iterative Markovian Fitting (D-IMF) approach. The input is a set of male faces from the CelebA dataset, and the output is a corresponding set of female faces. The D-IMF method achieves this translation using only 4 function evaluations (NFEs), a significant improvement over the existing Iterative Markovian Fitting (IMF) method, which requires 100 NFEs. The visual results demonstrate the quality of the generated female faces, which are comparable to those produced by the slower IMF method.

This figure shows the results of unpaired image-to-image translation using the proposed Discrete-time Iterative Markovian Fitting (D-IMF) approach. The input images are shown on the left, followed by the intermediate steps of the translation process (only a few steps are shown, represented by ‘…~80 more steps…’), and finally the output image on the right. The results demonstrate that the D-IMF method can achieve comparable quality to the standard Iterative Markovian Fitting (IMF) method, which requires many more steps (100), using only a small number of steps (4). The images are from the CelebA dataset, specifically male and female faces with a resolution of 128x128 pixels.

This figure shows the results of unpaired image-to-image translation using the proposed Discrete-time Iterative Markovian Fitting (D-IMF) approach. The input images are shown on the left, and the corresponding output images generated by D-IMF after only a few steps (NFE=4) are displayed on the right. The results are comparable to those achieved using the original Iterative Markovian Fitting (IMF) method, which requires hundreds of steps. The images are from the CelebA dataset [33], with male and female faces (128x128 pixels). The figure illustrates the efficiency of the D-IMF approach in terms of computation time and steps needed to achieve high-quality image translation.

This figure shows a comparison of image-to-image translation results using two different methods: the Discrete-time Iterative Markovian Fitting (D-IMF) approach and the Iterative Markovian Fitting (IMF) approach. The input is a set of male CelebA faces. The D-IMF method, proposed in this paper, achieves comparable results to the IMF method using only 4 steps (NFE=4), while the IMF method uses 100 steps (NFE=100). The images demonstrate that the D-IMF approach can efficiently perform image translation with fewer steps, leading to a significant reduction in inference time.

This figure shows a comparison of image-to-image translation results using two different methods: the authors’ proposed Discrete-time Iterative Markovian Fitting (D-IMF) approach and the Iterative Markovian Fitting (IMF) method. The input is a set of male CelebA faces. D-IMF achieves comparable results to the IMF method in just a few steps (4 steps vs. 80+ steps). This demonstrates the efficiency of the D-IMF approach.

This figure demonstrates the effectiveness of the proposed Discrete-time Iterative Markovian Fitting (D-IMF) approach for unpaired image-to-image translation. It shows example results of translating male faces to female faces using the CelebA dataset. The top row illustrates the input images, while the bottom row shows the results obtained by D-IMF within only a few steps. This is contrasted against the Iterative Markovian Fitting (IMF) approach, which requires significantly more (around 80) steps to achieve comparable results. The visual similarity of the results from both approaches highlights the efficacy of D-IMF in reducing computational costs while maintaining performance.

This figure shows the results of an unpaired image-to-image translation task using the proposed D-IMF (Discrete-time Iterative Markovian Fitting) approach. The input images are from the CelebA dataset, specifically male and female faces. The D-IMF method achieves comparable image translation quality to the original IMF method, but with significantly fewer steps (4 compared to 100). This demonstrates the efficiency gain of the proposed discrete-time approach.

This figure shows the results of an unpaired image-to-image translation task using the proposed Discrete-time Iterative Markovian Fitting (D-IMF) approach. The input images are on the left, and the output images generated by D-IMF are on the right. The D-IMF method requires only 4 steps to produce results comparable to the 100-step Iterative Markovian Fitting (IMF) method, demonstrating improved computational efficiency. The images used are from the CelebA dataset, specifically male and female faces with a resolution of 128x128 pixels.
More on tables

This table presents a comparison of the CBW2-UVP metric, which measures the discrepancy between the ground truth static Schrödinger bridge solution and the learned solution obtained by different algorithms, including the proposed ASBM method and several baselines on a benchmark dataset. Lower CBW2-UVP values indicate better performance. The results are categorized by the value of the parameter ’e’ and the dimensionality of the data ‘D’. The table highlights the proposed ASBM’s performance compared to other state-of-the-art algorithms.

This table presents the Fréchet Inception Distance (FID) scores for ASBM and DSBM models trained on the Colored MNIST dataset. The FID metric measures the similarity between the generated image distributions and the real image distributions, with lower scores indicating better performance. The table shows FID values for both models with two different values of the hyperparameter epsilon (∈), 1 and 10. This allows for comparison of the model performance under different levels of diversity in generated samples, as controlled by epsilon.

This table lists the hyperparameters used in the ASBM algorithm experiments. It includes the experiment name, the starting coupling method (Ind or MB), the number of outer and inner D-IMF iterations, the number of gradient updates for the discriminator and generator, the number of intermediate time steps (N), the batch size, the learning rates (Lr) for the discriminator and generator, the ratio of discriminator to generator optimization steps, and the exponential moving average (EMA) decay rate.
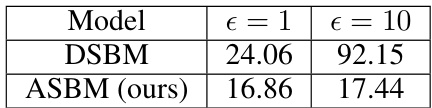
This table presents the FID (Fréchet Inception Distance) scores, a metric evaluating the quality of generated images, for a female-to-male image translation task on the CelebA dataset. Lower FID scores indicate better image quality. The results are broken down by model (DSBM and ASBM) and the value of the hyperparameter epsilon (ε), which controls diversity. The table shows that ASBM achieves lower FID scores than DSBM, indicating superior performance in generating realistic female-to-male face translations.

This table presents the CMMD (a metric similar to FID but with richer CLIP embeddings) for the unpaired CelebA image-to-image translation task. It compares the performance of the ASBM (proposed method) and the DSBM (baseline) models for two different values of the hyperparameter epsilon (ε). Lower CMMD values indicate better performance.

This table presents quantitative results of evaluating an ASBM model. The model was initially trained with 4 function evaluations (NFE). The table shows FID (Fréchet Inception Distance) scores and MSE (Mean Squared Error) cost for different numbers of NFEs during evaluation (1, 2, 3, 4, 8, 16, and 32). Lower FID indicates better image generation quality, and lower MSE indicates better similarity between input and output images.

This table presents the average LPIPS variance, a metric for measuring the diversity of generated images, for both DSBM and ASBM models. The results are shown for two different values of the coefficient epsilon (€), 1 and 10, demonstrating how the diversity changes based on the model and the value of epsilon. Lower LPIPS values generally indicate lower image diversity.

This table presents the perceptual similarity scores, measured using the Learned Perceptual Image Patch Similarity (LPIPS) metric, for both the DSBM and ASBM models. The results are broken down by the choice of epsilon (1 or 10) and indicate how well the generated images preserve the content of the input images from the CelebA test set for male-to-female translation.
Full paper#



















